参数在线调整的ARBF-NN车速预测方法研究

史立峰，马 彬，2，3，郭 兴，姜文龙

(1.北京信息科技大学 机电学院， 北京 100192； 2.新能源汽车北京实验室， 北京 100192； 3.北京电动车辆协同创新中心， 北京 100192； 4.中国人民公安大学 交通管理学院， 北京 100038)

0 引言

近年来，电动汽车因其节能环保的优势得到了快速发展，开发整车能量管理策略能够显著提高电动汽车能量利用效率。高精度车速预测是电动汽车能量管理控制策略的关键，是影响能量管理效果的重要因素[1]。因此，开发高精度车速预测方法对提高车辆能量管理效率具有重要意义。

目前，常用的车速预测方法可以区分为基于模型驱动的方法和基于数据驱动的方法[2]。其中，基于模型的车速预测方法依托于车辆与环境的相互关系建立模型，需要精确的地图信息以及昂贵的采集设备[3]。基于数据的车速预测方法利用历史车速数据或标准工况训练模型进行预测[4]，主要方法包括卡尔曼滤波法[5]、统计回归法[6]和神经网络算法[7]等。其中，神经网络算法由于其强大的非线性映射能力、鲁棒性和容错率，成为当前研究的热点[8]。当前，神经网络算法主要分为反馈型神经网络和前向型神经网络。在反馈型神经网络研究方面，解少博等[7]通过对比BP神经网络与线性回归、多项式回归预测方法，指出BP神经网络算法具有更高的预测精度；Ma等分别利用长短期记忆神经网络算法(LSTM-NN)和卷积神经网络算法(CNN)[9]实现了全路段交通速度预测。然而，反馈型神经网络需要通过大量具有代表性的样本数据对模型进行离线训练，在线的自适应性具有一定的局限性。相比之下，前向型神经网络具有收敛速度快、所需样本量少以及优良的在线模型训练能力。其中，RBF-NN作为典型的前向型神经网络，在车速预测方面表现出强大的优越性，并且预测结果更符合车辆行驶特性[10]。但是RBF-NN的输入层神经元数目、基函数标准差等结构参数是影响预测精度的关键参数[11-13]，当前依赖于经验的取值在全工况范围内难以获得满意的效果。因此，在线调节RBF-NN车速预测模型结构参数对于实现更精确的车速预测具有重要意义。

当前，赤池信息准则(AIC)和贝叶斯准则(BIC)能够作为模型参数调整准则，实现模型复杂度与预测准确性的平衡。在小样本情况下，通过AIC会选择高阶模型以提高预测精度；在多样本情况下，采用BIC可以防止因高精度而造成的模型复杂度过高[14]。根据此性质，本文选择AIC作为依据进行RBF-NN在线参数调整，进而提高车速预测精度。

基于上述分析，首先搭建车速采集系统进行实际工况车速数据采集，利用滑动时间窗口方法对采集车速数据进行样本化处理，建立预测模型训练样本库；其次，分析输入层神经元数目和基函数标准差对固定结构RBF-NN车速预测精度影响，进而结合AIC对RBF-NN结构参数进行在线调整。最后，提出了基于参数在线调整ARBF-NN的车速在线预测方法，提高了车速预测精度。同时，基于自然驾驶数据和标准测试工况，在Matlab仿真环境下验证了算法的有效性。

1 基于滑动时间窗口的车速样本化处理

1.1 自然驾驶数据采集

搭建图1所示自然驾驶数据采集实验系统对北京三环和四环城市道路的车速数据进行收集。系统包括IMU(车辆动态参数测量)、GNSS(导航车速等)和工控机。以1 s作为采样时间，收集的部分车速数据如图2(a)所示。为确保算法验证数据为包含低速、中速和高速的全工况城市道路车速数据，对三环自然驾驶数据中部分数据进行处理，以原数据作为中速工况，将原数据缩小60%倍作为低速工况，放大1.6倍作为高速工况，构建如图2(b)所示全工况车速数据，具体数据如表1所列。

图1 实验系统示意图

图2 实际车速轨迹

表1 不同工况车速信息

1.2 基于滑动时间窗口的车速样本化处理

滑动时间窗口是在每时刻对窗口内的所有数据进行处理，常用于数据量随时间增加而不断增大且数据时效性随时间衰减的应用场景。因此，选取滑动时间窗口方法进行历史车速数据处理(如图3所示)。

图3 滑动时间窗口样本构造

随着窗口的推移，产生h×1维输入向量，添加至训练模型输入矩阵之后；同理产生新的p×1维输出向量添加在旧的训练模型输出矩阵，测试模型始终是包含最新信息的h×1维输入向量。

假设在预测初始阶段没有预先储存车速数据，随着时间的推移逐渐形成历史车速数据库，用于RBF-NN的在线训练。时间长度为tn的历史车速数据库表示为：

V=(v(t1),v(t2),…,v(tn-1),v(tn))

(1)

式中：v(tn)表示第tn时刻的车速数据。

考虑历史hs车速数据对未来ps车速进行预测，则在ti时刻，训练模型的输入样本所属时间序列段为：

th=[ti-p-h+2,ti-p-h+2,…,ti-p]

(2)

训练模型输出样本所属时间序列段为

tp=[ti-p+1,ti-p+2,…,ti]

(3)

测试样本所属时间序列段为

(4)

经过滑动时间窗口的推移，在ti时刻，训练模型的输入样本和输出样本分别为：

(5)

(6)

测试模型的输入向量为：

Xtest=[v(ti-h+1),v(ti-h+2),…,v(ti)]T

(7)

2 具有参数在线调整功能的ARBF-NN车速预测方法

2.1 RBF-NN预测模型

RBF-NN算法是一种由输入层、隐藏层和输出层3层网络结构构成的前向型神经网络算法[15]。选取径向基函数作为模型的隐藏层，其网络结构如图4所示[16]。

图4 RBF-NN网络结构

RBF-NN的输出表达式为

(8)

式中：yk表示第k个输出层神经元的输出，即第k秒的预测车速；M表示隐藏层神经元数；ωjk表示第j个隐藏层神经元与第k个输出层神经元间的连接权值；φj表示第j个隐藏层神经元的输出，表达式为：

(9)

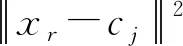
输入层神经元数目和基函数标准差，是影响RBF-NN预测精度的关键因素[17]。常用的计算基函数标准差的方式为

(10)

式中，dmax表示任意一对选定基函数中心的最大距离。

隐藏层与输出层之间的连接权值通过隐藏层输出矩阵与期望输出矩阵计算得到，表达式为

W=G+D

(11)

式中：W为连接权值矩阵；G为隐藏层输出矩阵；G+表示矩阵G的伪逆；D为期望输出矩阵。

2.2 RBF-NN结构参数对预测精度的影响

为说明预测的准确性，采用均方根误差(RMSE)作为评估指标来反映单步预测偏差，使用平均均方根误差(ARMSE)反映模型的整体预测性能。表达式为

(12)

(13)

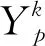
在车速预测研究中，考虑历史10 s的车速轨迹对未来5 s时域进行预测应用最为广泛[18]，因此，本文以5 s预测时域作为研究案例，即RBF-NN输出层神经元数目设置为5。为保证充分考虑历史车速轨迹的影响，输入层神经元数目(order)范围设置为3～13；此外，为保证基函数标准差(width)范围合理性且包含常用方式计算数值在内，本文设置基函数标准差范围为3～30。

输入层神经元数目和基函数标准差对预测精度的影响如图5所示，对单步车速预测结果的影响如图6所示。结果表明：输入层神经元数目和基函数标准差对预测结果有显著影响。输入层神经元数目过多会导致过拟合现象，过少会导致训练样本包含信息缺失。相同神经元数目下，随着基函数标准差的增大，ARMSE减小且趋于稳定，持续增大基函数标准差可能会导致高斯径向基函数过于平坦。

图5 不同输入层神经元数目和基函数标准差车速预测结果

图6 不同输入层神经元数目和基函数标准差单步车速预测结果

由图6结果可知，固定的输入层神经元数目和基函数标准差难以保证在整个过程中每一单步预测有最小均方根误差，无法实现整个过程的高精度预测。因此，需要合理选择对RBF-NN预测精度影响显著的输入层神经元数目和基函数标准差，提高模型在全工况下车速预测精度。

2.3 基于AIC准则的ARBF-NN在线参数调整

AIC作为衡量神经网络模型拟合优良性的一种标准，能够衡量所估计模型的复杂程度和模型数据拟合能力。因此，运用AIC准则来在线权衡RBF-NN模型的复杂度和车速预测结果的准确性。研究表明，AIC越小则表明预测模型越简单且预测结果越精确。因此，根据AIC结果进行RBF-NN参数在线调整。AIC表达式为：

(14)

预测过程中，计算每一单步预测的AIC值后，以最小AIC准则选取所对应的输入层神经元数目和基函数标准差，确定ARBF-NN结构参数。依据RBF-NN基本原理，本文设计了基于参数在线调整的ARBF-NN车速预测方法，预测方法整体流程如下所示。

Algorithm1基于参数在线调整的ARBF-NN 车速预测流程伪代码

Input:x:车速序列;p:初始输入层神经元数目,范围为[3,13];h:初始基函数标准差,范围为[3,30];M:基函数中心数目,定义为18;ti:当前时刻;tn: 车速序列长度;

Output:未来5 s 的预测车速;

1: setp=3,h=3,ti=h+p;

2: whileti<=tndo

3: forp=3;p<13;p++ do

4: forh=3;h<30;h++ do

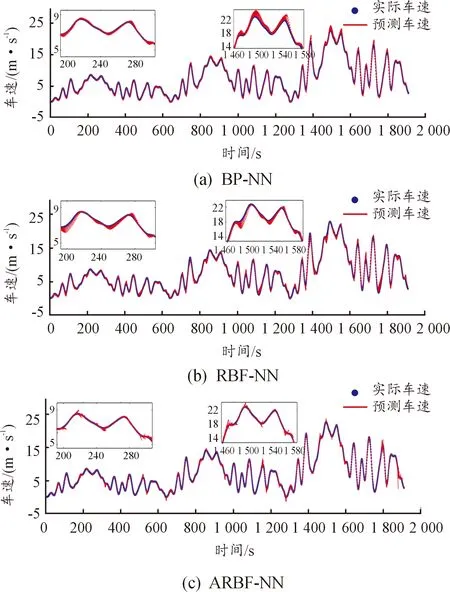
5: fort=1;t

6:Samplein(:,t)=x(t:t+p-1)

7:Sampleout(:,t)=x(t+p:t+p+h-1)

8:SDKin(:,t)=x(t+p+h:t+2*p-1)

9:SDKout=x(t+2*p:t+2*p+h-1)

10:Sampletest=x(t-h+1:t)

11: end for

12: 利用k-均值聚类算法计算基函数中心c

13:Z=dist(Samplein,c);

14:G=exp(-Z/2*h2); (计算隐藏层输出值)

15:W=pinv(G)*Sampleout; (计算隐藏层到输出层连接权值)

16:SDKZ=dist(SDKin,c); (结构确定模块确定结构参数)

17:SDKG=exp(-SDKZ/2*h2);

18:SDKout=W*SDKG;

19:err=SDKd-SDKout

20:ARMSE=sqrt(mean(err2))/ti-(h+p)

21:AIC=T*ARMSE+2*h

22:选择min(AIC)对应的h和p

23:ZZ=dist(Sampletest,c);

24:GG=exp(-ZZ/2*h2);(计算隐藏层输出值)

25:out=W*GG; (计算未来5 s 预测车速)

26: end for

27: end for

28:ti=ti+1

29: end while

3 仿真分析

3.1 ARBF-NN车速预测模型结果对比

为了验证ARBF-NN预测效果，选取BP和传统RBF-NN进行对比验证。由于车辆行驶行为存在一定内在规律，即在相同或者相似的历史车速轨迹下，未来短期有相同甚至相似的车速变化[10]。为使用合理样本对BP-NN车速预测模型进行训练以保证模型可以对车辆行驶行为内在规律进行有效学习，利用由2 710 s北京四环城市道路自然驾驶速度数据以及1 792 s WLTP、1 184 s NEDC和1 369 s UDDS测试工况组成的共7 055 s的车速数据对BP-NN车速预测模型进行离线训练，输出车速预测结果如图7(a)所示；对于RBF-NN车速预测模型，以最小ARMSE对应的结构参数(输入层神经元数目为5，基函数标准差为18)进行预测，预测结果如图7(b)所示；ARBF-NN车速预测结果如图7(c)所示。3种算法的车速预测结果如图8所示。

图7 BP-NN、RBF-NN和ARBF-NN车速预测结果

图8 BP-NN、RBF-NN和ARBF-NN车速预测结果

由结果可知，与其他2种预测模型相比，ARBF-NN车速预测精度获得明显改善。RBF-NN车速预测结果RMSE稳定在1 m/s以内，而ARBF-NN车速预测结果RMSE基本小于0.5 m/s，整体预测效果明显优于固定结构的RBF-NN预测方法。此外，在1 400 s及1 600～1 800 s阶段，车辆存在短时间内频繁加减速行为时，ARBF-NN预测精度效果提升明显。这说明ARBF-NN通过在线调整参数能够适应工况变化，实现更高精度的车速预测。

BP-NN、RBF-NN以及ARBF-NN在各工况下车速预测性能如表2所列。3种方法的预测结果ARMSE分别为0.375 8、0.384 9和0.175 3 m/s。所提出的ARBF-NN预测方法，相比于BP-NN精度提高53.36%，相比于RBF-NN精度提高54.47%。因此，所提出的ARBF-NN能够满足多工况的需求。

表2 BP-NN、RBF-NN和ARBF-NN车速预测结果

ARBF-NN预测方法参数调整过程如图9所示。结果表明，相比于RBF-NN车速预测方法，ARBF-NN车速预测方法从预测开始就有更小的AIC值，这表示ARBF-NN车速预测方法有更好的拟合效果，且在全过程中随车速变化可以实现输入层神经元数目和基函数标准差的实时调节，因而具有更高的预测精度。

图9 AIC计算结果及ARBF-NN参数选择结果

3.2 多工况下ARBF-NN预测效果分析

为了确保所提出车速预测方法的可靠性和稳定性，在北京三环、北京四环真实速度数据以及WLTP、UDDS标准工况车速4种工况下进一步证明ARBF-NN的高精度车速预测效果。5 s时域的预测结果分别如图10中(a)～(d)所示。由结果可知，北京三环车速预测结果RMSE基本小于1 m/s，由于车速变化趋势较平缓，预测效果优于构建的全工况车速；北京四环车速预测结果在200 ～400 s由于车速急剧变化，出现2次较大误差，其他时间段能保持较高精度预测效果；WLTP和UDDS工况下，车速预测结果RMSE基本小于2 m/s，预测精度稳定。表3列出了各车速数据下ARBF-NN预测结果ARMSE。结果表明，ARBF-NN对于多种车速数据下均有准确的预测精度。

图10 ARBF-NN车速预测模型在不同工况下预测结果

表3 ARBF-NN多种车速数据下预测结果

综上所述，本文提出的基于AIC的在线结构确定方法可以有效提高车速预测精度。

4 结论

提出了一种基于参数在线调整的ARBF-NN车速预测方法，实现基于自身历史车速数据的车速高精度在线预测。首先，搭建试验系统进行真实工况速度数据采集，利用滑动时间窗口方法将车速数据样本化；在分析输入层神经元数目和基函数标准差对车速预测精度影响的基础上，结合AIC准则对结构参数进行在线调整。最后，提出参数在线调整的ARBF-NN车速在线预测方法，实现了基于自车历史数据的车速高精度在线预测。4种工况的仿真结果表明，所提出的车速预测方法具有较高精度，相比于BP-NN精度提高53.36%，相比于RBF-NN精度提高54.47%，可为电动汽车车辆能量管理提供理论参考。

在未来的工作中，我们将探寻环境车辆与自车相对位置关系和相对速度关系与自车车速之间所存在的内在规律，预测环境车辆影响下车速拐点出现的时刻，即未来短时自车加减速变化，并对预测车速进行修正，以减小车速拐点处出现的较大预测误差，进一步提高车速预测精度。