湿滑道面飞机着陆滑水风险量化分析
2022-12-25胡宇祺
李 岳,胡宇祺,蔡 靖,戴 轩
(中国民航大学交通科学与工程学院,天津 300300)
飞机在湿滑道面着陆时可发生轮胎滑水,滑水会导致轮胎与道面失去接触,削弱刹车效用及方向控制力,造成飞机冲偏出跑道等严重事故。美国航空飞行员协会统计表明,飞机在积水道面起降时发生航空事故风险约为干燥条件下的4 倍,其中着陆阶段事故占比更是高达79%[1],因而有必要针对飞机着陆过程开展滑水风险分析。
在此领域,以往主要依托美国NASA(Nation⁃al Aeronautics and Space Administration)飞机轮胎滑水性能试验及临界滑水速度(以下简称vc)公式进行滑水判定,当飞机滑行速度超过vc时即认为构成滑水发生必要条件[2]。由于NASA 公式形式较为简略,仅反映单一胎压因素影响。对此,朱晟泽[3]基于NASA 试验开展不同侧滑角下细长体机身滑水性能研究,分析胎压、水膜厚度和宏观纹理对vc的影响。冯停[4]通过数值仿真探讨部分滑水轮胎vc与荷载条件之间相关关系。朱兴一等[5]开展基于真实路面纹理的飞机着陆滑水数值仿真,考察水膜厚度、轮胎滑移率及滑行速度对滑水性能影响。黄晓明等[6]对多因素影响下的轮胎滑水形成过程进行系统探讨。上述研究工作拓展了NASA公式适应条件,丰富了轮胎与道面流固耦合相互作用分析因素。由于滑水问题的复杂性,有研究将飞机滑行状态纳入vc考量。赵安家等[7]基于vc指标研究飞机结构、跑道状况和侧风因素与轮胎滑水形成关系。李岳等[8]通过滑水仿真提出适应飞机起飞与着陆不同滑行过程的vc上下限解概念。Hueb⁃ner 等[9]基于不同试验结果探讨vc判定方法。文献
[10]建立轮胎滑水临界状态理论模型,可针对不同机型预测vc结果。为改善跑道抗滑性能,降低滑水发生几率,有的学者研究侧重道面排水能力优化。Benedetto[11]研究路面排水能力增强与飞机滑水风险降低效果。Fwa 等[12]分析刻槽道面几何特征的滑水影响,通过增加刻槽宽度和深度提高vc值,进而提出适应抗滑要求的路面轮辙修复标准[13]。综合来看,现有研究主要通过完善vc指标应用条件解决复杂起降条件下飞机滑水安全分析问题,其不足之处在于仅能获得二元分析结论(即滑水或不滑水),难以支撑精细化滑水风险量化管理。
本文基于飞机起降数据和临界滑水速度提出滑水风险量化指标,将飞机接地滑行全过程纳入风险分析范围;建立适应着陆滑行阶段的飞机轮胎⁃积水道面流固耦合仿真分析模型,考察道面积水分布及接地位置漂移因素影响;通过一组算例阐明基于全概率公式的滑水风险量化分析过程。
1 滑水风险量化指标
轮胎滑水行为受飞机起降性能、滑行运动状态与道面积水状况共同影响,其形成机理极为复杂。基于美国兰利中心飞机轮胎滑水性能试验提出vc经验公式为

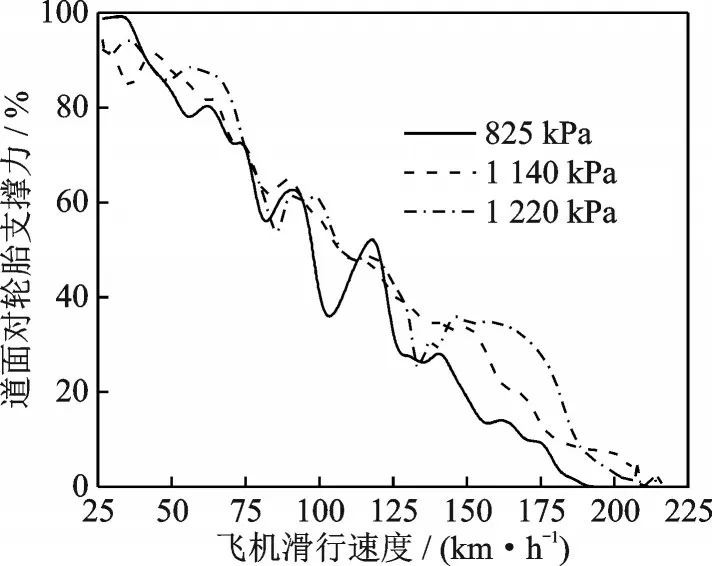
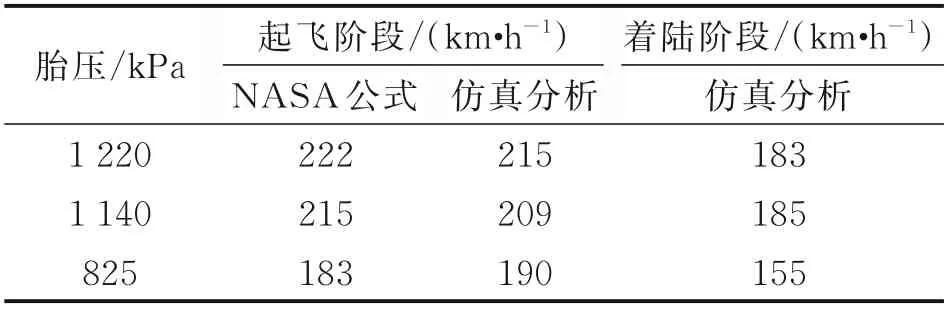
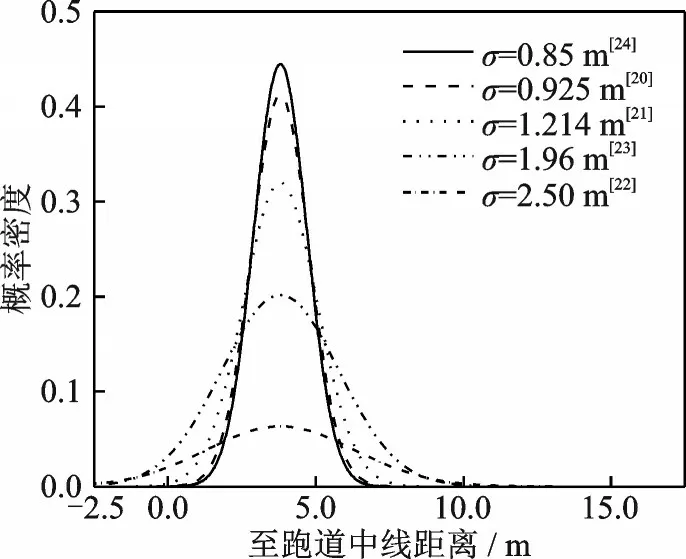
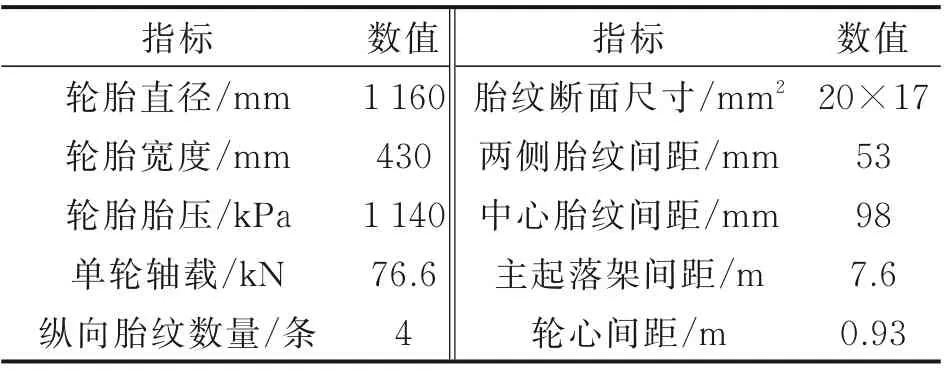
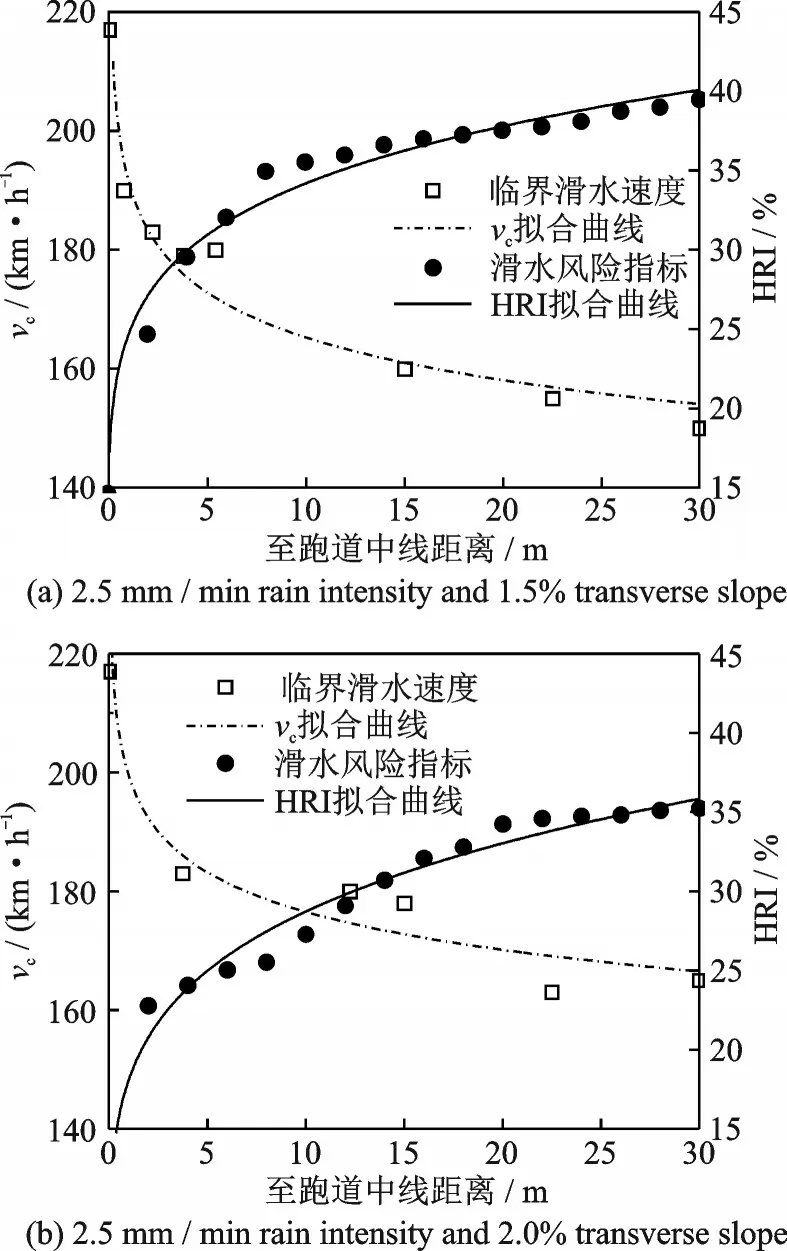
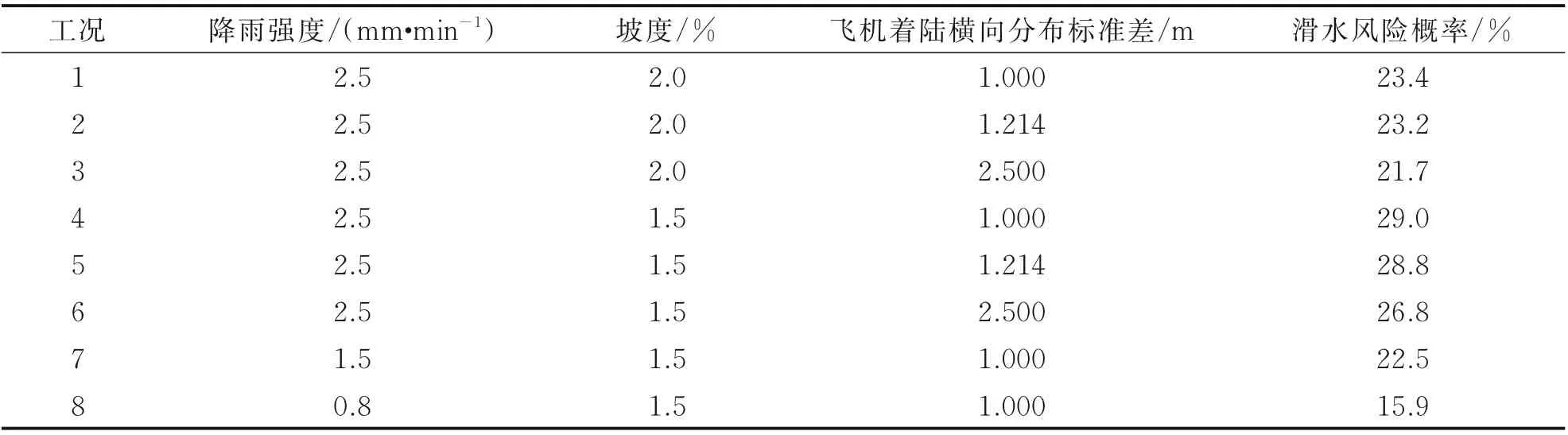
式中:v0为飞机接地速度;f(v0)为起降速度概率密度函数,可通过积分得到临界滑水速度超越概率P(v0>vc),α为滑水风险值,以飞机接地瞬时运动状态作为滑水判定依据。值得注意的是,在满足v0 图1 A320 飞机着陆QAR 数据Fig.1 A320 aircraft landing QAR data 图1 中,接地点速度在250 km/h 上下,至跑道近端距离约300 m;飞机接地后开启发动机反推及防滑控制措施,通过自动刹车系统实施减速,气象条件和人为因素导致不同着陆事件间QAR 曲线存在差异;速度降至70 km/h 以下时达到制动终止点,可根据机场布局和快滑道位置择机脱离跑道,滑行总长度约1 200 m,滑行速度与滑行距离对应关系如图1 所示。 根据QAR 曲线及vc计算高风险“窗口期”滑行距离在着陆全过程中占比,定义飞机滑水风险量化指标(Hydroplaning risk index,HRI)为 式中:K(v)为滑行距离函数,v1为跑道脱离速度。一方面,QAR 数据是对飞机起降性能与跑道运行状态的综合反映,同一条跑道上不同飞机具备不同QAR 数据特征,可通过数据统计分析获得代表值曲线;另一方面,道面横坡使得跑道中心至边缘积水厚度逐步增加,式中vc及K(vc)并非固定值且与飞机着陆接地位置密切相关。 该指标将飞机着陆滑行全过程纳入滑水风险分析范围,针对特定机型、积水状况和接地条件进行风险量化计算,滑水判别方式与以往明显不同。 当前轮胎滑水仿真分析包含轮胎冲击模型和水流冲击模型2 种主流方式。有研究表明,二者计算道面支撑力变化规律和vc结果相互等效,且后者计算成本更低[14]。故本文采用水流冲击方式模拟飞机轮胎流固耦合滑水行为,基于ABAQUS 软件建立仿真分析模型形式如图2 所示。 图2 飞机轮胎滑水有限元模型Fig.2 Finite element model of aircraft tire hydroplaning 轮胎及道面采用拉格朗日网格离散,轮胎中心与轮毂耦合,轮胎内部等效为具有统一本构的均质橡胶材料[7],采用Mooney⁃Rivlin 模型模拟橡胶材料超弹性变形特征[15];上部积水层与空气层采用无匹配离散欧拉网格建模,轮胎滚动方向两端分别设置水泵区和压力出口,通过调节水流冲击速度模拟不同轮胎滑行状态,转动角速度与水流速度匹配,滑移率保持为1.0。轮胎与积水层物理力学参数在文献[16]已详细说明,此处不再赘述。依据《国际民用航空公约(ICAO)》附件14 考察2 种道面横坡度情况,1.5%和2.0%,积水分布计算结果见3.1 节。 图3 给出了道面对轮胎支撑力随滑行速度变化曲线,模型参数依据NASA 试验条件确定。采用ASTM 标 准E⁃524 规 格 轮 胎,模 拟3 种 胎 压 条件,滑行速度由25 km/h 逐步增大至250 km/h,积水层厚度7.6 mm。 图3 道面支撑力随滑行速度变化曲线Fig.3 Variation curves of pavement supporting force versus taxing speed 图3 中,积水对轮胎冲击作用随滑行速度增加而增大,支撑力曲线呈现振荡下降趋势;剩余支撑力不足5%时可认为轮胎已接近临界滑水状态,此时滑行速度即为vc值。表1 中依次列举了水流加速与减速冲击条件下vc分析数据,对应飞机起飞与着陆滑行过程,并与NASA 公式结果进行比较。 表1 临界滑水速度结果对比Table 1 Comparison of critical hydroplaning speed results NASA 滑水试验采用逐步加速方式,符合飞机起飞阶段滑行特征。以NASA 公式结果为基准,3 种胎压条件下水流加速仿真所得vc与前者相差可在4% 左右,符合以往研究误差控制范围(10%以下),表明该模型计算精度可满足滑水分析需要。对于飞机着陆阶段,水流减速冲击时vc较加速冲击时仿真结果低12%~18%,与文献[1]给出的相差15%结论较为一致,符合研究规律。因此后续研究均采用减速冲击方式模拟着陆过程中轮胎滑水行为,作为滑水分析最不利工况。 滑水风险分析目的在于计算飞机在不同着陆条件下发生滑水事故的可能性,从滑水形成物质基础(积水状况)和诱发条件(接地状况)两方面入手,计算影响因素共同发生的累积概率,实现滑水风险量化目标。 降雨引起道面积水是飞机滑水事故的诱发条件之一,积水厚度与降雨强度、道面坡度和地表径流等因素相关。采用平面二维浅水方程计算道面横向积水分布,假定降雨与排水达到动平衡状态,积水保持相对静止且流速不为零,道面横向各截面流量固定(不考虑纵坡),忽略风应力、科氏力和二阶扩散项,修正二维浅水方程计算式为[17] 式 中:h为 流 体 层 厚 度;vx、vy为x与y方 向 流 体 速度;S0x、S0y为x与y方向上坡度源项;Sfx、Sfy为x与y方向的摩擦源项;q(t)为降雨强度,参考吴建军等[18]提出的短时强降雨强度标准,选取0.8、1.5 和2.5 mm/min 3 种情况进行道面积水分布计算,编制Matlab 程序求解道面积水横向分布如图4所示。 图4 道面积水横向分布Fig.4 Transverse distribution of water film on pavement 图4 中,道面积水厚度自中心至边缘非线性增加;0.8 mm/min 降雨强度时1.5%横坡道面中心与边缘积水厚度差2.3 mm,随着降雨强度进一步增大,两者相差增至0.8 mm/min 时的2.0 倍和3.0倍,不均匀分布特征增强;道面横坡为2.0%时,同等降雨强度条件下中心与边缘积水厚度差低于1.5%横坡情况,增大道面横坡度有利于加快横向排水,积水分布差异缓和。 显然,仅采用NASA 公式计算vc结果存在局限性,跑道中线至边缘轮胎滑水极限明显不同,临界滑水速度应为关于接地位置横坐标函数vc(x),风险指标HRI(x)也随之变化。应分段开展滑水仿真计算,作为风险量化分析基础。 如前文所述,v0>vc是飞机滑水事故另一诱发条件。在着陆末段飞机尽力与跑道中线对齐,受气流干扰和人为操控影响仍可在小范围内发生摆动,由接地瞬时姿态决定轮胎实际作用位置及滑行路径[19]。因此需考虑飞机接地滑行位置横向漂移分布,以确定滑水风险累积概率。基于不同跑道起降数据统计得出单个飞机轮胎接地位置横向分布如图5 所示[20⁃24]。 图5 飞机接地位置横向分布Fig.5 Transverse distribution of aircraft landing position 图5 中,飞机接地位置呈现正态分布特征,符合美国联邦航空管理局基于轮迹统计分析给出的飞机主轮横向分布规律[19],概率密度峰值点位置由主力机型主起落架间距确定;当标准差小于1.0 m 时,接地分布宽度不超过7.0 m,最大概率密度小于0.45;接地分布宽度随标准差增加而增大,概率密度峰值随之减小;部分机场标准差达到2.5 m,此时一侧起落架接地偏移范围已“跨过”跑道中线,并与另一侧接地横向分布曲线相互叠加,增大滑水风险分析难度。 研究表明飞机主起落架外侧轮胎滑水可早于其他轮胎发生,对飞机整体滑行安全最为不利[13]。据此以空客A320 机型主起落架外侧轮胎为案例开展滑水风险量化分析。轮胎基本参数如表2所示。 表2 A320 主起落架轮胎参数Table 2 Parameters of A320 main landing gear tire 依据图4 中道面积水厚度分布,采用本文建立的滑水仿真分析模型,分段求解不同接地位置vc结果并进行非线性拟合。对照QAR 代表值曲线,计算滑水风险指标HRI(x)结果并在图6 中绘出。 图6 临界滑水速度与HRI 分布Fig.6 Distribution of critical hydroplaning speed and HRI 与道面积水分布规律对应,vc自跑道中线至边缘呈指数型下降趋势,与Fwa 等[13]研究相符;以1.5% 横坡道面为例,跑道边缘vc较中线位置低57.7 km/h,当飞机出现较大幅度横向偏移时,可导致一侧起落架轮胎超出滑水界限条件;跑道中线两侧约10 m 宽接地带范围内,滑水风险指标HRI 低于30%,至跑道边缘位置HRI 值增加至35%以上,飞机在跑道边缘接地时滑水事故几率明显高于中线区域。 沿宽度方向将跑道划分为n个小段,从图6 可以得出各分段HRI(xi)代表值,根据飞机接地位置分布概率密度函数ω(x),通过积分得出各分段接地概率P(xi),此时第i段风险概率为 将各分段HRI(xi)与P(xi)相乘得到飞机轮胎滑水风险值贡献率分布,结果如图7 所示。 图7 轮胎滑水风险贡献率分布Fig.7 Probability distribution of contribution ratio of hydro⁃planing risk of aircraft tire 图7 中,轮胎滑水风险贡献率峰值出现在飞机着陆位置最大概率处(接地带区域),跑道边缘位置虽然HRI(xi)较大,但接地概率P(xi)极低,对轮胎滑水风险贡献率较低,与道面积水厚度并非正相关关系;跑道中线位置HRI(xi)与P(xi)均较小,因而轮胎滑水贡献率也保持在较低水平。 表3 列举了多种工况组合下滑水风险结果,分析可知:(1)同等降雨强度条件下滑水风险概率随横向分布标准差增大而减小,降幅分别为1.7%和2.2%;(2)同等横向分布标准差条件下增大道面横坡度有助于促进积水排除和降低滑水风险,2.0%工况较1.5%工况风险值降低5.1%~5.6%,符合Benedetto[11]的研究结论;(3)对比工况4、7 和8 结果降雨强度因素与飞机滑水风险概率正相关,降雨强度由0.8 mm/min 增至2.5 mm/min 时滑水风险增加13.1%;(4)工况4 滑水风险概率高于其他工况,为表3 中抗滑最不利条件,符合单因素分析规律。 表3 不同工况下跑道整体滑水风险概率Table 3 Overall probability of hydroplaning risk of runway under different conditions 综合来看,上述分析方法可针对特定道面状况、降雨条件和着陆机型实施滑水风险量化计算。与以往滑水判定方式相比,该方法可定量描述道面横坡及接地位置偏移等因素影响,判定方式符合滑水事故统计规律[25]。滑水风险分析是提出安全措施的理论基础[26],基于该方法可支撑飞机滑水风险精细化评价。 (1)本文提出了基于飞机起降数据和临界滑水速度的滑水风险量化指标,将飞机接地滑行全过程纳入分析范围,改进以往二元滑水判定方式。 (2)本文建立了适应着陆滑行阶段的飞机轮胎⁃积水道面流固耦合仿真模型,探讨道面积水分布与飞机接地位置横向漂移对滑水风险的影响。 (3)案例分析结果表明同等降雨强度条件下滑水风险概率随飞机接地横向分布标准差增大而减小;增大横坡可加快积水排除并降低滑水风险,降雨强度与飞机滑水风险正相关;基于全概率公式可对上述因素影响实施定量分析。 为简化分析条件,本文仅探讨由横坡度引起道面积水一维不均匀分布问题。由于道面纵坡及轮辙等的共同作用,实际积水情况要复杂得多,将在后续研究中探讨二维不均匀积水下滑水风险问题。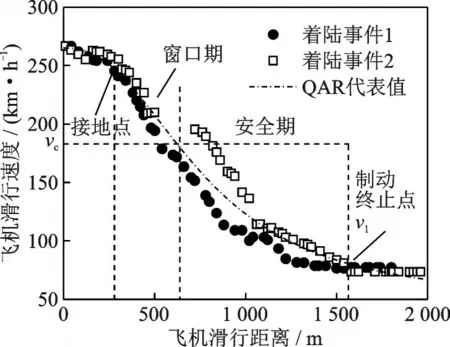
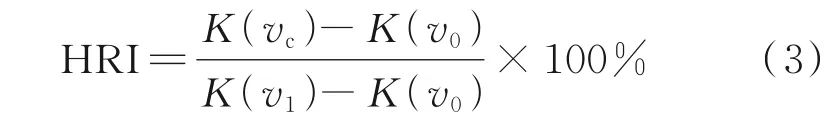
2 滑水仿真模型
2.1 基本参数

2.2 模型验证
3 滑水风险量化分析
3.1 道面积水状况分布
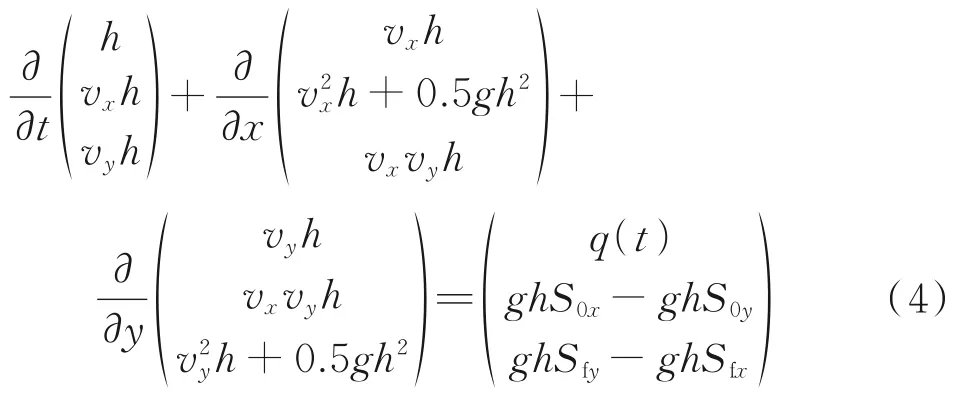

3.2 接地滑行位置分布
3.3 案例分析


4 结 论
