关于林分蓄积量的相关因素的统计分析＊

陈峻纬，高雨欣，陈林一

（苏州大学数学科学学院，江苏 苏州 215006）

2022年经历了近年来最热酷暑，人类面临着恶劣气候的挑战，如何应对极端生态环境，是世界各国一直在思考探索解决的问题。联合国关于气候变化，呼吁增氧减排二氧化碳，而林业为人类生态起到了不可磨灭的作用。森林的科学合理规划在这里相当重要，其中林分蓄积量是研究森林碳汇[1]的基础，也是森林最优轮伐的一个重要决定因素。有很多学者研究了林分蓄积量：如惠淑荣等[2]等在《GM（1，1）模型和Logistic函数在日本落叶松林分蓄积量预测中的对比研究》一文中对林分蓄积量采取的是GM（1，1）模型；陈烨铭[3]选择了逻辑斯蒂函数进行研究；刘四海等[4]选择Richards函数进行研究；林卓等[5]用ARIMA方法进行建模预测。相关文献虽对林分蓄积量进行了研究，但都仅对林龄与蓄积量的关系进行了研究，未对林分蓄积量及其影响因素之间的统计关系进行分析。

基于林分蓄积量的研究现状，本文对林分蓄积量、小班面积、郁闭度、林龄、胸径、树高、密度之间的关联进行统计分析，探寻规律。为研究林分蓄积量及其相关因素的关系，运用多元统计[6]中的线性回归分析、相关分析、逐步回归分析、因子分析、聚类分析方法结合SPSS[7-8]软件操作得到相关结论，以为林业经营者制定合理的森林计划提供参考。

1 统计分析

数据来源：简盖元在《森林碳生产研究》[6]中的2010年福建省杉木主产区三明市12个国有林场的小班数据，如表1所示。

表1 12个国有林场的小班基本情况

标记变量：x1为平均小班面积（hm2），x2为平均郁闭度，x3为平均林龄（年），x4为平均胸径（cm），x5为平均树高（m），x6为平均密度（株/hm2），y为平均林分蓄积量（m3/hm2）。

标记地区：A1为沙县官庄国有林场，A2为沙县水南国有林场，A3为清流国有林场，A4为泰宁国有林场，A5为永安国有林场，A6为尤溪国有林场，A7为大田桃源国有林场，A8为大田梅林国有林场，A9为宁化国有林场，A10为明溪国有林场，A11为建宁国有林场，A12为将乐国有林场。

数据的标准化：因数据单位不一致，对其进行标准化处理，下文的分析都是基于标准化处理后的数据。下文首先进行回归分析研究变量之间的影响关系。分为3步：首先是线性回归分析，其次是相关分析，最后是逐步回归分析[7-8]。

1.1 线性回归分析

线性回归分析[7-8]用于研究影响变量对被影响变量的影响关系。将x1、x2、x3、x4、x5、x6作为自变量，而将y作为因变量进行线性回归分析，表2给出了直接进行线性回归的相关数据，从表2可见，尽管模型R2为0.845，意味着x1、x2、x3、x4、x5、x6可以解释y的84.5%变化原因，但由于对模型进行F检验时发现模型并没有通过F检验（F=4.552，p=0.059＞0.05），所以线性回归并不适用，考虑先使用相关分析讨论变量之间的相关关系。

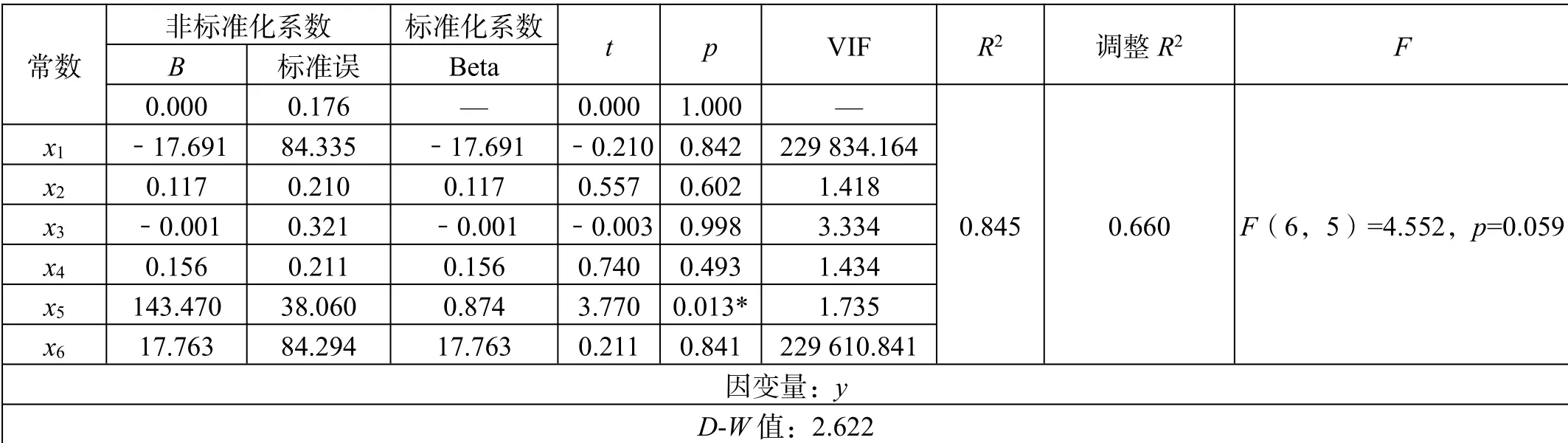
表2 线性回归分析结果（n=12）

1.2 相关分析

相关分析[7-8]用于研究定量数据之间的关系情况，是否有关系，分析相关关系为正向或负向，通过相关系数大小说明关系紧密程度。本文利用SPSS中的相关分析去研究y（被影响变量）分别和x1、x2、x3、x4、x5、x6共6项影响变量之间的相关关系，使用Pearson相关系数去表示相关关系的强弱情况，如表3所示。

表3 Pearson相关

根据表3具体分析可知：y和x1之间的相关系数值为﹣0.097，接近于0，并且p值为0.764>0.05，因而说明y和x1之间并没有相关关系。y和x2之间的相关系数值为0.129，接近于0，并且p值为0.691>0.05，因而说明y和x2之间并没有相关关系。y和x3之间的相关系数值为0.600，并且呈现出0.05水平的显著性，因而说明y和x3之间有着显著的正相关关系。y和x4之间的相关系数值为0.280，接近于0，并且p值为0.379>0.05，因而说明y和x4之间并没有相关关系。y和x5之间的相关系数值为0.899，并且呈现出0.01水平的显著性，因而说明y和x5之间有着显著的正相关关系。y和x6之间的相关系数值为﹣0.096，接近于0，并且p值为0.765>0.05，因而说明y和x6之间并没有相关关系。y分别和x3、x5共2项之间的相关关系显著性较强；y分别和x1、x2、x4、x6共4项之间的相关关系不显著。可见要建立线性模型需要对自变量进行筛选。

1.3 逐步回归分析

逐步回归[7-8]会自动识别出有显著性的自变量，不具有显著性的自变量会自动移出模型，方法有逐步stepwise法、forward向前法和backward向后法，本文选择stepwise法。逐步回归分析结果如表4所示。

表4 逐步回归分析结果（n=12）

由表4可知，R2=0.809说明自变量对林分蓄积量y的影响程度较强，模型拟合情况理想VIF值为1（﹤5），说明无多重共线性。经过模型自动识别，最终余下x5共1项在模型中，R2为0.809，意味着x5可以解释y的80.9%变化原因。而且模型通过F检验（F=42.281，p=0.000<0.05），说明模型有效。

模型公式为：y=0.000+147.695×x5。

x5的回归系数值为147.695（t=6.502，p=0.000﹤0.01），意味着x5会对y产生显著的正向影响关系。

根据上文分析可见，x5平均树高对林分蓄积量y的影响显著，通过树高就可以根据模型估计出林分蓄积量，森林从业者在经营森林时更多的关注点应放在如何提高树的纵向生长上。下面使用因子分析中的因子载荷观察各变量之间的距离，以研究它们的影响关系。

1.4 因子分析

使用因子分析[7-8]可以进行信息浓缩研究，首先分析研究数据是否适合进行因子分析，本文利用SPSS中的因子分析去研究y（被影响变量）以及x1、x2、x3、x4、x5、x6共6项影响变量，得到KMO为0.522，大于0.5，但是小于0.6，满足因子分析KMO值大于0.5的基本要求。本文进行因子分析的研究目的是寻找与被影响变量y最近的影响变量，通过因子分析计算因子得分如表5所示。

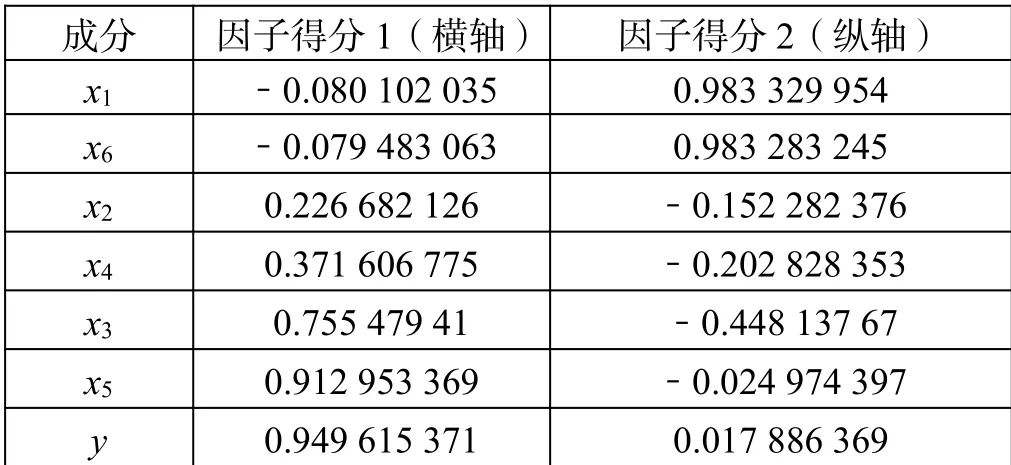
表5 因子得分

载荷图用于展示各因子与载荷值的关系情况，根据表5计算的因子载荷作图如图1所示，其中x1、x6靠得很近，x1被x6遮挡。

图1 因子载荷图

从上图可见，x5与y之间距离最近，实际上，与前面的回归分析结论一致。前文运用线性回归分析、相关分析、逐步回归分析得到x5与y的线性关系显著，又通过因子分析的载荷图直观可见二者之间距离很近，更清晰地呈现出密切联系。下面利用聚类分析研究一下这12个林场之间的关系。

1.5 聚类分析

使用聚类分析[7-8]对12个林场进行分类，使用Kmeans聚类分析方法，聚类类别基本情况汇总如表6所示。

从表6可以看出：最终聚类得到3类群体，其中6个林场A1沙县官庄国有林场、A2沙县水南国有林场、A5永安国有林场、A7大田桃源国有林场、A8大田梅林国有林场及A12将乐国有林场为一类，占比50.00%；其中5个林场A3清流国有林场、A6尤溪国有林场、A10明溪国有林场、A9宁化国有林场、A11建宁国有林场为一类，占比41.67%；A4泰宁国有林场单独为一类，占比8.33%。同一类别的林场之间经营结果类似，不同类别的林场之间应加强交流，取长补短，互相学习。

表6 聚类类别基本情况汇总

2 结论与展望

本文运用多元统计中的线性回归分析、相关分析、逐步回归分析、因子分析、聚类分析方法结合SPSS软件操作对林分蓄积量、小班面积、郁闭度、林龄、胸径、树高、密度之间的关联进行研究，得到树高对林分蓄积量的影响显著，其他因素影响力不显著，并给出了树高与林分蓄积量的数学模型，可以利用模型由树高近似估计林分蓄积量，再决定森林的下一步规划。又根据聚类分析的结论对三明市的12个林场进行分类，不同类别之间应该互通有无、互相学习。