具有几何约束的非等面积界面布局优化方法

韦曦，孙靖

具有几何约束的非等面积界面布局优化方法

韦曦1，孙靖2

（1.宿迁学院，江苏 宿迁 223800；2.江苏海洋大学，江苏 连云港 222005）

由于计算的难度与精度问题，在求解布局的过程中通常不考虑待布局元素面积的大小和形状的几何约束问题，导致求解的布局结果是理论上的，无法达到真正实用的目的。为提高界面布局优化方法生成布局方案的可用性，提出了一种集成启发式算法、多属性决策（MAMD）和整数线性规划（ILP）的方法。首先，在获取到待布局元素间相关性、待布局元素的使用频率和面积等数据情况下，使用遗传算法（GA）通过改变待布局元素几何约束的参数生成一组备选布局方案；其次，将交互成本、GA寻优所花费的时间、有效性、效率和满意度作为评价界面布局的五个指标，根据TOPSIS、AHP和数据包络分析（DEA）等多属性决策方法对所有备选布局方案进行排序；最后，使用ILP方法获取一致性排序。获得一个有效、具有高可用性的布局方案。根据实验结果可知，该方法寻到的最优布局方案比原始方案有效地降低了交互成本和算法寻优的时间，提高了布局方案的可用性。

用户界面；几何约束；多属性决策方法；遗传算法；布局优化；可用性

用户界面（UI）布局的重点在于如何在有限的显示区域内有效地实现信息的布局[1]。为包含多个控件和指示器的控制面板（CP）建立最佳配置是一个复杂的问题。近年来，一些学者对设施布局进行了广泛研究，这些研究主要集中在平面图上待布局元素间的相对位置，如梁永强等[2]提出一种图标利用率与易搜索率进行匹配的布局设计方法。但当布局问题的复杂性增加时，最常用的求解布局的方法是建立UI交互的定量模型，使用启发式算法寻找提供最佳模型性能的配置[3]，如邓丽等[4]根据人的认知规律总结出布局原则并建立相关的数学模型，使用遗传和蚁群算法加以求解。这些研究主要集中在人机界面上待布局元素间相对位置的寻优，但却忽略了元素的面积大小和几何约束（长宽比）问题，一般假设待布局元素的面积相等[4-5]或使用原始待布局元素面积的大小[6]。这样求解出的布局是理论上的，在实际生产中，不符合实际布局的情况，需要后期手动加以调整。目前，也有一些学者研究具有非等面积的界面布局问题。但Diego等[7]在其文献中指出，关于布局优化的研究要么忽略了几何限制，要么对各元素的几何比例建立了一个不合理的区间。此外，在启发式算法求解布局的过程也存在一些问题。首先，用于收集数据的一些方式，会使获得的数据呈现一定的主观性或者不精确[8]。其次，使用启发式算法求解得到的结果一般是在可接受计算成本内的最好的解，但无法判断所得解的可行性和最优性[9]。基于以上考虑，本文提出了一种基于遗传算法–多属性决策–整数线性规划（GA–MADM– ILP）的具有几何约束的非等面积用户界面布局优化集成方法。

1 方法概述

为了寻求具有高可用性的布局优化方案，针对现存方法在求解布局过程中存在的问题，提出一种基于GA–MAMD–ILP集成的布局方法，详细流程见图1。

这项工作中提出的方法分3个阶段。在第1阶段，确定合适布局原则；第2阶段，收集相关数据用于求解基于几何约束的非等面积UI布局优化问题。在第3阶段，通过TOPSIS、AHP和DEA等多属性决策方法对备选方案进行排序，然后，使用ILP对3种方案排名寻找一致性排序结果。

图1 本文方法的流程

1.1 问题描述

本研究给定需要优化的控制面板（CP），见图2。其控制面板上有指示器及操作按键两个类型的元素。CP的长度为，宽为，面积为，需要布局元素的数量为，为待布局元素几何比即长宽比（/），s为待布局元素在CP上所占面积的大小。这些待布局元素的形状是矩形的，且是具有灵活长宽比的矩形。此处的灵活是该矩形的长宽比在一定区间内可以自由变化，且每个矩形的长宽比可能不同。当设备的长宽比不固定时，就有可能获得满足元素更严格几何约束的解[10]。

图2 多功能钻机控制面板，每个元素为一个AOI

为了获取可用性高的布局方案，收集以往文献对元素长宽比（）值设置的数据，为本文值的设置提供理论指导，见表1。Rusu等[11]认为最优的长宽比应该为1，这样的比值可以提高图形的可读性和理解性；Tate和Smith在文献[12]中为布局提供了设施最大允许长宽比的数值参考，他们认为设施的最大允许长宽比或者最大宽长比超过3是把设施布置在过长的单元内，会造成面板面积一定程度的浪费，不适宜于任何类型的生产工作。Diego等[10]在其研究中表明，在长宽比小于3的情况下寻到了交互成本最小的布局方案，而Diego等[13]在其研究中，将待布局元素根据其类型的不同将最大允许长宽比设置为6。这一数值的设定与Tate和Smith等的研究[12]结果产生了矛盾。所以，本文在以上文献基础上，不预先设定值，而是在1到6之间进行实验。针对在特定面积下何种长宽比能寻到最优的布局方案进行实验，根据以往文献提供的数据并且考虑到计算难度与计算时间等问题，在1到3之间时，将值的步长设置为0.1，而在3到6之间的步长设置为0.5，进行实验。

表1 以往文献中对待布局元素长宽比值的设置

Tab.1 The setting of length-width ratio (R) of AOIs discussed in previous literatures

在本文中，考虑到所有待布局元素放置的方向都是自由导向的（水平或垂直放置）且=，所以，所有待布局元素长宽比的取值为[min,max]，min和max分别为待布局元素的最小和最大长宽比。为保证每个待布局元素布局的灵活性，其长宽比可以在该区间内取任意值。<1时，即元素为垂直放置，>1时，元素为水平放置，见图3。

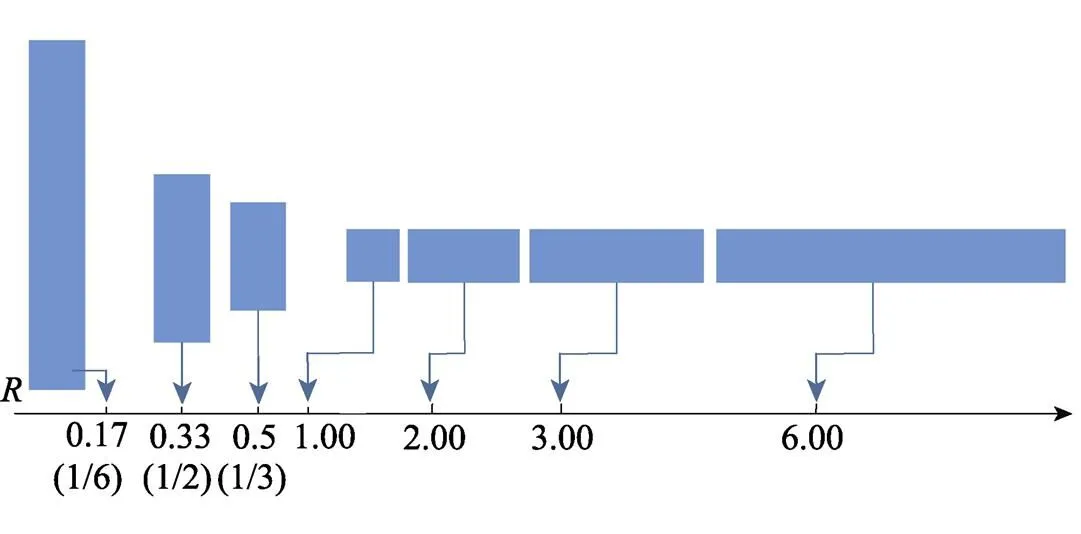
图3 待布局元素形状的长宽比(R)在最小和最大长宽比之间的变化

1.2 确定布局原则

不了解界面布局原则，不服从人的认知因素的界面布局，势必会导致性能和用户体验的下降[14]。本研究使用界面布置的基本设计原则和基于认知心理学的相关知识[4]共同建立以下布局设计原则。

原则1：重要性和使用频率原则。元件的尺寸大小应根据其重要性和使用频率确定，重要性和使用频率的综合权重越高，元件的尺寸应该越大。

原则2：相关性原则。两元素间相关性的高低与元素间顺序访问的次数成正比。相关性越高，元素间在界面上的位置必须彼此靠近，即两元素间相关性越高距离越近。

1.3 生成备选布局方案

在此阶段，根据上文中的布局原则，构建目标函数，用于在UI空间内找到在满足所有约束条件交互成本最小的布局方案。以下是该阶段的详细步骤。

1.3.1 数据收集

步骤1，使用眼动追踪设备获取相关性和使用频率数据。

为了获取布局所需的相关数据，此节使用眼动追踪设备进行第1次眼动实验，收集待布局元素间的访问顺序及使用频率等数据。这是一种非侵入式的数据收集方式，收集到的数据更加合理。

步骤2，多属性决策–熵混合方法确定待布局元素的重要性和使用频率数据。

在计算待布局元素的面积时，为了避免一些重要性高的元素占据大部分界面，而一些使用频率高但重要度程度低的元素变得不切合实际的小，考虑到元素的重要性程度和使用频率之间没有必然的线性关系。因此，采用重要性和使用频率综合权重值确定元素面积的大小。本文使用多属性决策与熵值法混合的方法来确定待布局元素重要性和使用频率的综合权重。采用多属性决策的方法获取待布局元素的主观权重，同时采用熵值法获得客观权重，然后将主观权重和客观权重进行线性计算，得到待布局元素的综合权重。

1）多属性决策方法确定重要性和操作频率的主观权重。由位专家和操作员根据个待布局元素在使用过程中的重要性程度给出评分，分值在1～100分。分值越大表示元素越重要。构建重要性决策矩阵[a]，分值呈现正态分布状态。对[a]进行归一化处理得到矩阵[]。根据步骤1，可获得使用频率矩阵[]=[f]。

由于参与评分和执行任务的人员数量是相同的，并且是同一组人。所以，重要性和使用频率的综合权重矩阵可表如下：

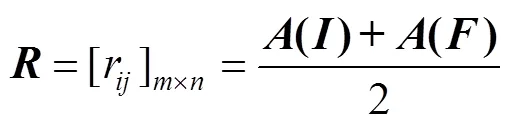
待布局元素的重要性和使用频率的综合权重值可以定义如下：

2）熵值法确定重要性和操作频率的客观权重。

对于待布局元素，其重要性和使用频率的综合权重如下：

1.3.2 构建及求解目标函数

此阶段的目标是寻到满足所有约束条件下交互成本最低的布局方案。

方案1，约束条件。

使用算法求解布局问题时，需要使所有待布局元素在CP内寻优，不能超出CP的边界且所有元素间不能发生重叠。

边界约束。任意摆放的一个待布局元素同时满足以下两个约束则不会超出边界。

重叠约束。对于两个待布局元素和，满足以下任一约束条件便不会发生重叠情况。

几何约束。对于任意一个待布局元素，其长宽比R都在指定取值范围内，不能超出该取值范围。

方案2，构建目标函数。

在既定的CP空间内，为使交互成本达到最小，每个待布局元素放置时需考虑元素间的相关性。相关性越高，元素间的距离应越小。优化的目标是使界面布局的交互成本达到最低。目标函数见式（13）

方案3，使用GA求解目标函数。

因为布局优化问题是一个NP–hard问题，因此本文通过使用GA求解方案2中目标函数。通过改变的参数，获得一组不同值的备选布局方案并计算每个备选布局方案的最小交互成本。

1.3.3 评估指标

该评付指标的目的是评估上文中生成的所有备选布局方案的优劣。

1.3.3.1 确定评估指标

第一，Tompkins等[16]研究表明，一个有效的布局可以将制造成本降低10%～30%；交互成本的高低可以反映用户与界面交互绩效的高低；因此，交互成本可以作为评价界面布局交互绩效高低的一个重要指标。第二，因为本文是针对具有几何约束的布局优化方法研究，所以本文设置了不同的取值；GA寻到最优解所花费的时间可以作为评判几何约束设置合理性的一个指标。第三，针对目前多变的用户需求，仅根据交互成本来评价布局的优劣是不合理的[5]，因为评价一个界面布局效果的好坏取决于人与界面的交互性能，而布局优化的主要目的是提高界面的可用性[17]。可用性定义涉及三个方面的指标，即效率、有效性和满意度。

本文将完成指定任务所花费的时间作为评估布局方案的效率指标；用户在特定界面上完成指定任务时出现的错误次数可以作为一个有效性的指标，情境后问卷（After-Scenario Questionnaire，ASQ）[18]可以衡量用户在使用界面完成任务时的满意度，必须使用这三个不同指标对界面进行可用性进行评估。针对本文有面积大小和几何约束的特点，对ASQ中的3个问题做一定调整：“问题1，总体来说，我对完成这些任务的容易程度感到满意；问题2，总体来说，我对完成这些任务所用的时间感到满意；问题3，总体来说，在完成任务时，在特定的距离下，我对能清晰感知到界面中所有待布局元素所呈现关键信息感到满意。”受测者使用李克特量表从1（非常满意）-7（非常不满意）对3个问题给出评分，得分越低满意度越高。

1.3.3.2 计算评估指标

在1.3.2节方案3中由GA求解目标函数的过程中得出交互成本和寻优时间。

效率、有效性和满意度通过GA生成所有满足约束条件的备选布局方案后，为了评估每个备选布局方案的可用性，对个受测者进行第2次眼动实验。在第2次眼动实验中，受测者在每一个备选布局方案上执行与眼动实验1相同15项任务，记录受测者在每个备选布局方案上完成任务所花费的时间、出现的错误次数和每个受测者在完成任务后完成一份ASQ，ASQ最终得分为3个问题得分的平均值。最终，将布局库中所有备选方案与每个布局方案对应的5个评估指标数据生成一个决策矩阵。

1.4 备选布局方案排序

该阶段是本文的最后阶段，该阶段需要实现的目的是根据1.3.3节中提出的5个布局评估指标和多属性决策方法对1.3节中生成的所有备选布局方案进行排序。为了克服多属性决策方案的主观性，使用三种多属性决策方法（AHP、TOPSIS和DEA）分别对所有备选布局方案进行排序[19]。其中，AHP和TOPSIS为参数的多属性决策评价方法，数据包络分析（DEA，Data envelopment analysis）为非参数的多属性决策评价方法，最早由查恩斯、库珀和罗德斯于1978年提出，它是一种非参数MADM评估方法，可用于评估多输入多输出（单输出）系统的有效性。最终，使用ILP对3种结果获取一致性排序。

为了获得最终排序结果，需要对上述三种多属性决策方法获得的排序结果进行聚合处理，使用整数线性规划的方法[20]对三种布局方案进行一致性排序，见式(14)。

2 实例运用

为验证本文所提出方法的有效性，以某应急救援设备的控制面板为例进行布局优化。利用软件将该CP进行仿真（见图2），利用眼动追踪软件检测控件上的动作和被控过程中控件在相应的空间中响应。为了提高界面的空间利用率，不考虑原始面板布局中的空白区域（AOI17–AOI18）。CP上总待布局元素的个数=16，= 810 mm，=384 mm，=311 040 mm2。CP的总长宽比为2.11。座椅相对于CP的距离可进行调整，操作员标准坐姿情况下，距离取值为500 mm。

选择20个有该类型钻机操作经验的操作员或专家，在CP上执行15个预定义任务，这些任务包括常见任务、紧急任务和不能犯错的关键任务。

2.1 布局原则

本文的2个布局原则见1.2节。

2.2 布局方案

步骤1，获取相关性数据和使用频率数据。20名受测人员全部参与实验，每人都需完成15项预定义的操作任务。其中，常用任务8项、机器故障状态下的任务5项、不能出错的关键任务1项和在短时间内应完成的紧急任务1项。收集全部操作者完成任务期间的眼动追踪与鼠标点击数据，从而计算得到每对AOIs间的双向转换矩阵。针对20位操作者，AOIs间的平均转换矩阵见表2，AOI与自身不存在相关性。同时，收集20位受测者在完成任务期间对16个待布局元素的访问次数。根据收集到每个待布局元素的访问次数计算所得16个待布局元素的使用频率矩阵，见表3。其中，操作者只有在每一个AOI上的注视停留时间超过300 ms才会被认为是AOIs之间的转换。当受测者认为他们自己完成所有任务时点击键盘空格键结束实验。受试者眼动追踪实验的结果见图4。

表2 待布局元素（AOIs）间的转换矩阵

Tab.2 Conversion matrix between AOIs

注：数值取小数点后2位。

步骤2，多属性决策–熵混合方法确定待布局元素的重要性和使用频率数据。

上述20名操作员和专家根据以往使用经验，对16个待布局元素进行重要度评分，构建重要度矩阵，并对矩阵进行归一化处理，见表4。

根据表3—表4和式（1）计算可得16个待布局元素的重要性和使用频率综合权重矩阵，见表5。

根据表5和式（3）—（8）计算可得20个受测者的权重，见表6。根据式（9）计算可得16个待布局元素重要性和使用频率的综合权重值，见表7。根据Z和CP的总面积，计算可得每一个待布局元素在CP上所占面积，见表7。

表3 待布局元素（AOIs）的使用频率矩阵

Tab.3 The use frequency matrix of AOIs

注：数值取小数点后2位。

注：a图中包括热点图，鼠标点击点（黄色圆点）和鼠标运动轨迹（白色线）；b图AOIs间的转换次数，黄色线越粗代表AOIs之间的转换次数越多。

表4 待布局元素重要性评分的归一化矩阵

Tab.4 Normalized matrix of the importance score of AOIs

注：数值取小数点2位。

表5 重要性和使用频率综合权重矩阵

Tab.5 Importance and comprehensive weight matrix of use frequency

注：数值取小数点2位。

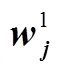
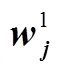
Tab.6 Optimal subjective weight and optimal objective weight

注：数值取小数点2位。

表7 待布局元素的重要性、使用频率综合权重和优化后待布局元素的面积

Tab.7 Importance and comprehensive weight of use frequency of AOIs and area of AOIs after optimization

20名领域类专家和操作员作为受试者进行第2次眼动实验。使用眼动设备记录每一个受测者在每个备选布局方案上完成指定15项任务时所花费的时间和出现错误的次数，每个受测者在完成测试任务后被要求填写一个ASQ。出现的错误类型包括受测者没有清晰识别AOI中的关键信息造成的错误、鼠标点击操作出现的错误和没有完成指定的任务而出现的错误。最终，所得完成指定任务所花费的时间、错误率合ASQ得分（取3个问题得分的平均值），见表8。

2.3 方案排序

方案1 AHP，20个专家与操作员对5个评估指标进行两两比较打分，构建判断矩阵。表9给出了5个评估指标的权重，并对判断矩阵进行一致性检验。对每个布局方案的5个评估指标进行加权求和，见表10。

方案2 TOPSIS，将归一化处理后的矩阵与专家给出的每一个评估指标的权重相乘，构造加权正态化决策矩阵；从加权正态化决策矩阵中，找出理想解和负理想解，并计算每个布局方案与正理想解和负理想解的距离，并利用负理想解与正理想解和负理想解之和的比值确定所有备选布局方案进行排序，结果见表11。

表8 20个备选布局方案的评估指标

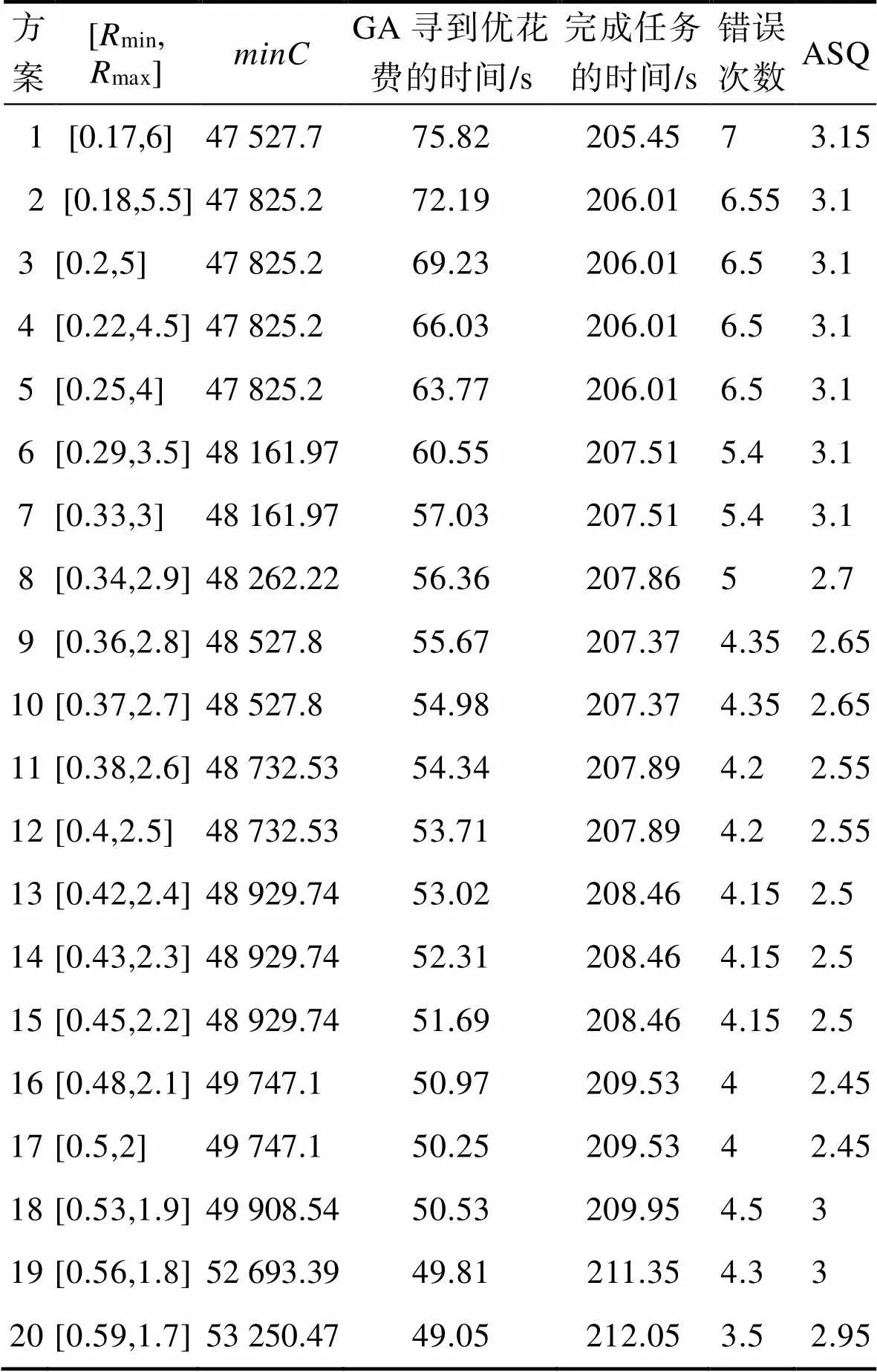
Tab.8 Evaluation factors of 20 alternative layout schemes

注：数值取小数点2位。

方案3 DEA，确定输入量：交互成本、GA所需的寻优时间、完成指定任务的时间、完成指定任务中出现的错误次数以及用户的ASQ评分；确定输出量：为了确定所有备选布局方案的有效性，将输出量统一设置为1；计算的效率指数值并对备选布局方案进行排名，结果见表12。

Step4 ILP

使用式（14）对上述三种多属性决策方法进行一致性求解，结果见表13。

表9 AHP计算所得权重

Tab.9 Weight calculated by AHP

注：CI=0.0050 CR=0.0044最大特征值=5.02。

表10 使用AHP对所有备选布局方案的排名

Tab.10 Ranking of all alternative layout schemes by AHP

表11 使用TOPSIS对所有备选布局方案的排名

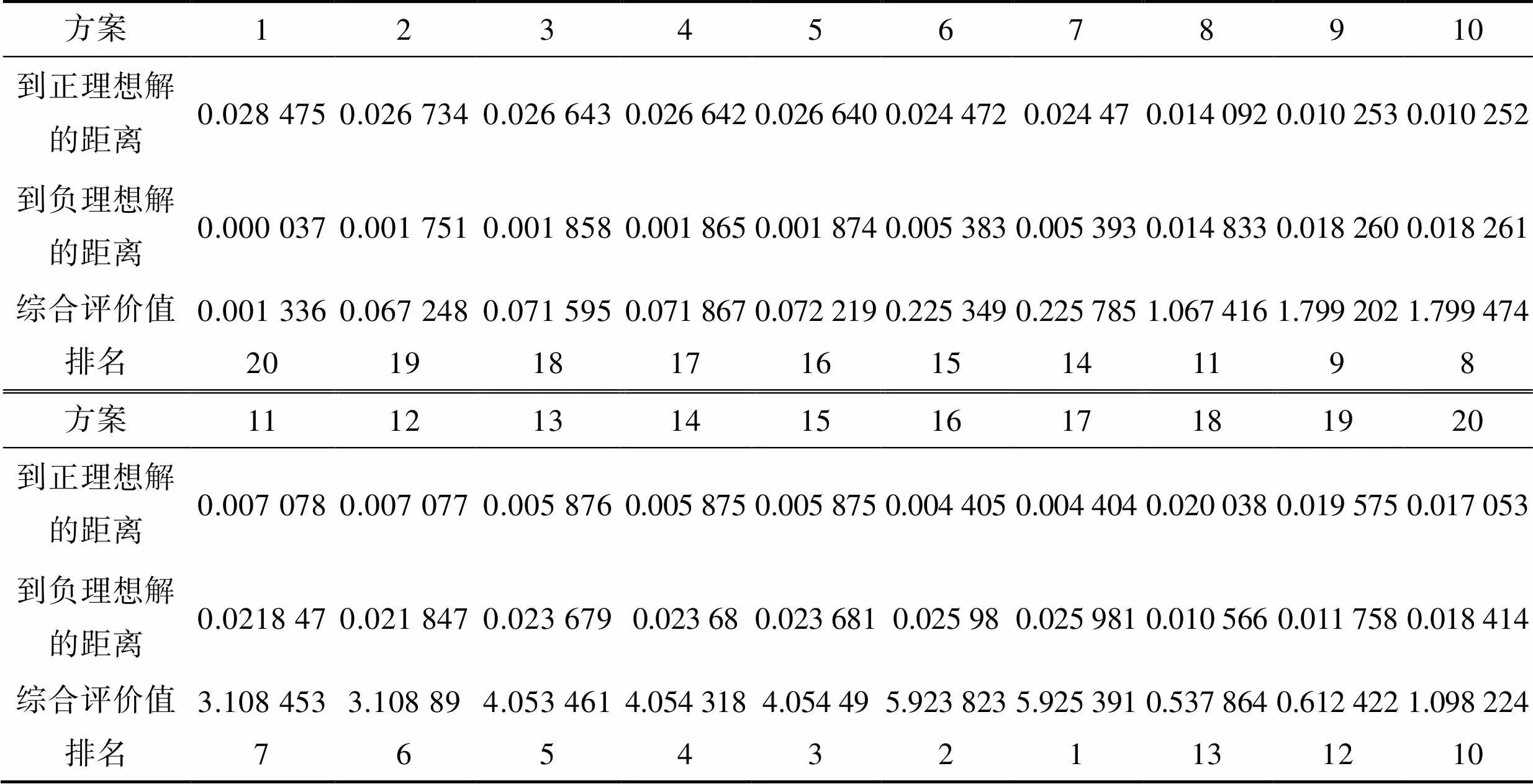
Tab.11 Ranking of all alternative layout schemes by TOPSIS

注：数值省略到小数点后6位。

表12 使用DEA对所有备选布局方案进行的有效性排名

Tab.12 Effectiveness ranking of all alternative layout schemes by DEA

表13 20个备选布局方案的共识排名

Tab.13 Consensus ranking of 20 alternative layout schemes

3 结果

将本文寻到的最优布局方案——第17个备选方案与原始界面的5项评估指标指值进行对比，见表14，数据来自第2节实验1和实验2中。本文5个评价标准都为低优指标，即数值低的为理想解。将原始布局方案与本文方法得出的最优布局方案做对比，由表14可见，使用本文方法获得的最优布局在交互成本、寻优时间、完成任务的所需的时间、错误次数和ASQ得分等5个指标上都明显优于原始布局。根据以上对比结果可知，本文方法得到最优布局方案比原始方案有效地缩短了完成任务的时间、减少了发生错误的次数和提高了用户的满意度、方案的可用性。

表14 原始布局方案与最优布局方案的对比

Tab.14 Comparison of the original layout scheme and the optimal layout scheme

4 讨论

本文采用5个指标综合评价布局方案，从中选出对5个指标综合满意度最高的布局方案，而并非只考虑交互成本一项指标。从表8和表13中可知，当取值在2到3之间时，排名结果较好，而3时的布局方案排名结果整体优于3时。当3时的交互成本相对≤3平均增长了0.03%，3时的交互成本优于≤3，而当3时，随着值增大而导致取值范围增大，发生错误的次数和ASQ得分比≤3时的平均增加了0.58%和0.16%。从这些数据可发现当3时，交互成本增长率的百分比远远小于发生错误的次数和ASQ得分增长的百分比。所以，综合这几项指标来看，当3相对≤3时的排名更低。这一数值结果也验证了Tate and Smith等提出的元素长宽比（或者宽长比）大于3是将元素放置于过长的单元内，不适宜于任何类型的生产工作。分析上述数据可知，长宽比设置的不同，会影响用户与界面的交互性能和可用性，而设置一个合适的长宽比取值范围则可以获得具有高可用性的布局方案。

将原始布局方案与本文方法选出的最优布局方案进行对比，从表14可发现，最优布局方案比原始方案减少了11.25%的交互成本，使用算法寻优所需的时间减少了14.89%，而用户完成指定任务的效率增加了3.43%，完成指定任务的有效性增加了26.25%，用户对最优布局方案的满意度与原始布局相比，增加了73.47%。从这些数据中可得出结论：本文方法寻到的最优布局较之原始方案不仅降低了交互成本和算法寻优的时间，完成任务的时间、错误次数和ASQ也有不同程度的降低，方案的可用性有着明显的提升。

此外，本文方法也存在一些局限性，在计算每个待布局元素的面积时是将所有待布局元素铺满整个CP，没有考虑待布局元素间的间距和留白等因素。本文中得出的最优元素值与CP的比例有关，CP的长宽比不同，求解出的最优的取值可能是不同的。在下一步的工作中，将实验在不同界面比例下，何种长宽比取值能获得高可用性的布局方案。

5 结语

本文以提高布局优化方法生成布局方案的适用性和可用性为目的。本文方法在优化布局时考虑了每个待布局元素的元素面积和几何约束。因此，得到的优化布局可以直接使用，不需设计人员再进行后期的手动调整。本文提出了一种新的确定UI上每个待布局元素面积（MAMD–Entroy混合方法）的方法，并通过不断改变的参数值，使用GA获得一组不同长宽比情况下的布局方案；然后以三种多属性决策方法针对五个指标对备选布局方案进行排序，最终使用ILP获得共识排序，找出长宽比在[0.5,2]时得到了可用性最高的布局方案。通过实验可发现，通过本文方法获取的布局方案与原始方案相比，不仅降低了交互成本和算法寻优的时间，完成任务的时间、错误次数和ASQ也有不同程度的降低，提高了方案的可用性。

[1] NIU Ya-feng, XIE Yi, XUE Cheng-qi, et al. Investigation on the Neurophysiological Correlates of Similarity Cognition of Digital Interface Color and Layout[J]. Advances in Mechanical Engineering, 2018, 10(11): 168781401880320.

[2] 梁永强, 李培林, 王崴, 等. GUI中图标利用率与易搜索率匹配设计方法[J]. 计算机辅助设计与图形学学报, 2018, 30(1): 155-162.

[3] LIANG Yong-qiang, LI Pei-lin, WANG Wei, et al. Design Method of Matching Icon Utilization and Easy Search Rate in GUI[J]. Journal of Computer-Aided Design & Computer Graphics, 2018, 30(1): 155-162.

[4] FRANCIS G. Designing Multifunction Displays: An Optimization Approach[J]. International Journal of Cog­nitive Ergonomics, 2000, 4(2): 107-124.

[5] DENG Li, WANG Guo-hua, YU Sui-huai. Layout Design of Human-Machine Interaction Interface of Cabin Based on Cognitive Ergonomics and GA-ACA[J]. Com­putational Intelligence and Neuroscience, 2016, 2016: 1032139.

[6] KUMAR R. Sustainable Robust Layout Using Big Data Approach: A Key towards Industry 4.0[J]. Journal of Cleaner Production, 2018, 204: 643-659.

[7] 陈德钧, 方卫宁, 秦永贞, 等. 轨道车辆司机操纵台人机界面布局优化模型与算法[J]. 铁道学报, 2014, 36(11): 40-47.

[8] CHEN De-jun, FANG Wei-ning, QIN Yong-zhen, et al. Optimizing Model and Algorithm for Human-Machine

[9] Interface Layout of Metro Train Driver's Desk[J]. Journal of the China Railway Society, 2014, 36(11): 40-47.

[10] DIEGO M J A, SANTAMARINA S M C, ALCAIDE M J, et al. Solving Facility Layout Problems with Strict Geometric Constraints Using a Two-Phase Genetic Algorithm[J]. International Journal of Production Research, 2009, 47(6): 1679-1693.

[11] ALPPAY C, et al. An Ergonomics Based Design Research Method for the Arrangement of Helicopter Flight Instrument Panels[J]. Applied Ergonomics, 2015, 51: 85-101.

[12] 沈秀敏. 基于整数线性规划方法的集装箱装载布局优化问题研究[D]. 大连: 大连海事大学, 2013.

[13] SHEN Xiu-min. Research on Layout Optimization of Container Loading Problem Based on Integer Linear Programming Approach[D]. Dalian: Dalian Maritime University, 2013.

[14] DIEGO M J A, SANTAMARINA S M C, CLOQUELL B V A, et al. Slicing Tree's Geometric Potential: An Indicator for Layout Problems Based on Slicing Tree Structure[J]. International Journal of Production Research, 2008, 46(4): 1071-1087.

[15] RUSU A, et al. A Straight-Line Order-Preserving Binary Tree Drawing Algorithm with Linear Area and Arbitrary Aspect Ratio[J]. Computational Geometry, 2015, 48(3): 268-294.

[16] TATE D M, SMITH A E. Unequal-Area Facility Layout by Genetic Search[J]. IIE Transactions, 1995, 27(4): 465-472.

[17] DIEGO M J A, et al. User-Interfaces Layout Optimization Using Eye-Tracking, Mouse Movements and Genetic Algorithms[J]. Applied Ergonomics, 2019, 78: 197-209.

[18] YAN Sheng-yuan, et al. Effect of User Interface Layout on the Operators’ Mental Workload in Emergency Operating Procedures in Nuclear Power Plants[J]. Nuclear Engineering and Design, 2017, 322: 266-276.

[19] KENNEDY A. Eye Tracking: A Comprehensive Guide to Methods and Measures[J]. The Quarterly Journal of Experimental Psychology, 2016, 69(3): 607-609.

[20] Tompkins J A. Facilities planning: A vision for the 21st century[J]. Iie Solutions. 1997, 29(8): 18-19.

[21] 普丹丹, 张富豪. 涤纶织物/PVC复合材料的动态机械性能及其在界面评价中的应用[J]. 丝绸, 2021, 58(10): 18-22.

PU Dan-dan, ZHANG Fu-hao. Dynamic Mechanical Properties of Polyester Fabric/pvc Composites and Their Applications in Interface Evaluation[J]. Journal of Silk, 2021, 58(10): 18-22.

[22] LEWIS J R. IBM Computer Usability Satisfaction Que­stionnaires: Psychometric Evaluation and Instructions for Use[J]. International Journal of Human-Computer Interaction, 1995, 7(1): 57-78.

[23] 汪坤, 史伟民, 李建强, 等. 基于深度学习的织物印花分割算法研究[J]. 现代纺织技术, 2021, 29(3): 45-50.

WANG Kun, SHI Wei-min, LI Jian-qiang, et al. Research on Fabric Printing Segmentation Algorthm Based on Deep Learning[J]. Advanced Textile Technology, 2021, 29(3): 45-50.

[24] KAUR H, SINGH S P, GLARDON R. An Integer Linear Program for Integrated Supplier Selection: A Sustainable Flexible Framework[J]. Global Journal of Flexible Systems Management, 2016, 17(2): 113-134.

Non-equal Area Interface Layout Optimization Method with Geometric Constraints

WEI Xi1, SUN Jing2

(1.Suqian University, Jiangsu Suqian 223800, China;2.Jiangsu Ocean University, Jiangsu Lianyungang 222005,China.)

Because of the difficulty and precision of calculation, the size of AOIs and geometric constraints are usually not considered in the process of solving the layout, which leads to the theoretical layout results and cannot achieve the real practical purpose. The work aims to propose a method integrating heuristic algorithm, multiple attribute decision making (MADM) and integer linear programming (ILP), so as to improve the availability of interface layout optimization method to generate layout scheme. At first, under the condition that the data such as the correlation between AOIs, the use frequency and the size of the area of AOIs were obtained, a set of alternative layout schemes were generated with genetic algorithm (GA) by changing that parameters of the geometric constraint of AOIs. Secondly, the interaction cost, time of GA optimization, effectiveness, efficiency and satisfaction were taken as the five criteria to evaluate the interface layout, and all the alternative layout schemes were ranked according to multiple attribute decision making such as TOPSIS, AHP and Data Envelopment Analysis (DEA). Then, the ILP method was used to obtain consistent ranking. Thus, an effective and highly available layout scheme was obtained. According to the experimental results, it can be found that compared with the original scheme, the optimal layout scheme can effectively reduce the interaction cost and algorithm optimization time, and improve the availability of the layout scheme.

user interface (UI); geometric constraints; multiple attribute decision making (MADM); genetic algorithm (GA); layout optimization; availability

TB472

A

1001-3563(2022)24-0075-12

10.19554/j.cnki.1001-3563.2022.24.009

2022–07–06

国家自然科学基金面上项目（61873105）

韦曦（1984—），女，硕士，讲师，主要研究方向为广告设计、品牌设计等。

责任编辑：陈作