光学自由曲面的加工参数对光散射的影响
2022-12-22李迎春李吉祥孙江波王增路张壮壮
李迎春, 李 欣*, 李吉祥, 孙江波,王增路, 张壮壮, 刘 非
(1.长春工业大学 机电工程学院, 吉林 长春 130012;2.吉林交通职业技术学院 机械工程学院, 吉林 长春 130012)
0 引 言
光学自由曲面是指没有任何回转对称性的光学曲面,该光学曲面作为一个典型特征表面,不仅简化了系统结构,降低了系统的重量,增加了设计自由度,还极大地改善了光学系统的光学性能[1]。如果要求零件可以满足光学特性的条件,则必须依赖高水平精度的加工来保证。椭圆振动切削最初是由日本学者提出的[2-3],它改善了刀具与加工表面的摩擦状态,使得表面质量进一步提高,同时有效降低切削力和减小切削热及刀具的磨损,被广泛认为是实现光学自由曲面精密加工的有效方法之一[4]。在光学自由曲面的精密加工(无论是椭圆振动切削或者其他类型切削)过程中,由于刀具形状误差和机床的固有频率振动等因素存在,不可避免地会导致工件表面产生一系列不规则的形貌特征,对最终产品的光学性能产生严重的影响。光学元件的表面特征可以认为是由低频、中频及高频分量叠加而成[5-6]。每一类几何形貌特征的形成都是多种因素综合作用的结果,如图 1所示。

图1 表面形貌特征及其影响因素
光学零件表面的几何形貌与其光的散射性能存在着重要的联系。当光照射在光学器件的表面,尤其是在粗糙的表面上,会产生散射现象,在这种情况下,由于高频的误差,例如表面的粗糙度会造成较大的角散射,而中频的误差则会造成较小的角散射[7],进而对光学系统性能造成一定的影响。关于表面散射的研究已经很多,其中瑞利-莱斯理论应用于超平滑的表面,也就是表面的高度波动比入射波波长的1/100小[8]。贝克曼-基尔霍夫的散射理论[9]也可以应用于粗糙表面,但由于存在近轴的假定,在入射的角度过大,会产生与实验不符的现象[10],而Harvey-Shack散射理论则是一种可以应用于任意角度、不同粗糙表面的散射理论[11]。利用Harvey-Shack散射原理,从频带误差的角度评估光学表面的光学特性,以确定其是否满足光学性能指标。近几年,我国国防科技大学对精密光学元件的加工、检测与评价进行了较深入的研究[12-14]。根据哈维-沙克散射原理和统计光学原理,对不同频率分量误差与光学特性的内在联系进行了初步探讨。吴冬良[15-16]教授提出一种简单的加工误差与环围能量比、散射损失比的关系式,但由于是全局评价的参量,其相关长度难以全面反映各频域的分布,因而不能反映出某一频段的局部误差对环围能量比及散射损失比的影响。
文中根据高斯滤波原理对经由刀具路径仿真获得的光学自由曲面加工表面形貌模型在频率空间上进行划分,获得只含有粗糙度加工表面。对仿真获得的加工表面做均方根偏差分析和点扩散函数分析,便得到椭圆振动切削加工过程中加工参数(如进给量和刀尖圆弧半径)对于光学元件的光学性能的影响规律。研究成果可以为椭圆振动切削的加工误差分析提供一种新的思路,促进光学自由曲面的高精密、高可靠性的椭圆振动切削加工技术的发展,对实现可预测光学性能的光学元件的椭圆振动切削加工具有一定的指导意义。
1 理论方法
光散射是指光线通过不均匀的介质而偏离其原来的传播方向,并重新产生空间分布的现象。对于光学成像系统,当光线经过带有粗糙度的光学元件表面时,将会发生光散射,使得图像对比度和分辨率降低,成像质量下降。Harvey-Shack散射理论是以傅里叶变换为基础的散射理论,Harvey和Shack对表面散射现象提出了线性系统理论[17],将表面散射看作是标量衍射过程,从而得出与表面形貌散射特性有关的“表面传递函数”,将表面形貌与散射特性关联。Harvey-Shack散射理论是一种适用于任何角度入射光和各种粗糙度面的散射理论[18]。文中使用表面传递函数对应的点扩散函数作为目标函数来分析加工参数对加工表面光散射的影响。
在分析粗糙的光学加工表面时,一般将粗糙的表面看成是一种随机的过程,由于其随机性,可以借助统计规律描述粗糙表面。表面轮廓及相关统计如图2所示。
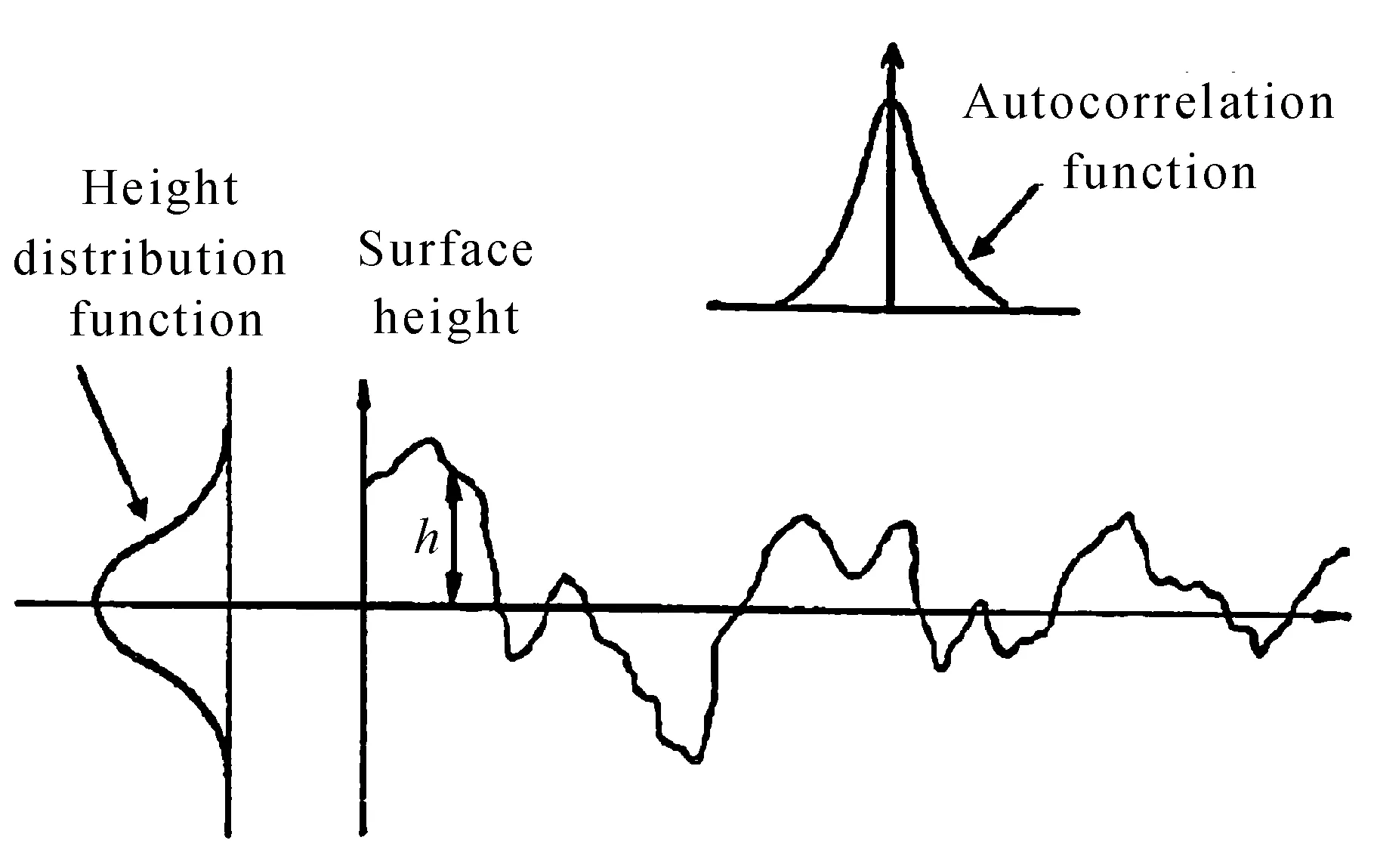
图2 表面轮廓及相关统计
自相关函数表示的是粗糙表面轮廓上一个给定位置的轮廓高度与其相邻的另一位置的轮廓高度值之间的关联程度,自相关函数为
C(Δx,Δy)=E[z(x,y)z(x+Δx,y+Δy)],
(1)
式中:Δx,Δy----粗糙表面两点坐标在x轴、y轴方向上的差值。
对自相关函数进行归一化处理,得到相关系数为
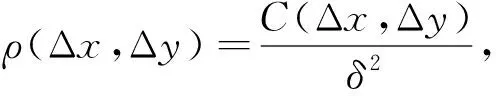
(2)
式中:δ2----表面高度起伏均方差;
δ----粗糙度表面均方根。
当Δx=0,Δy=0时,C(0,0)=δ2。相关系数在Δx=0,Δy=0具有最大值1,随着Δx,Δy的增大,ρ(Δx,Δy)逐渐减小。当相关系数降至1/e时,Δx,Δy为表面相关长度,记作lx,ly。
在实际的粗糙表面轮廓计算中,为了计算方便,常将连续的表面形貌离散化,则离散二维粗糙度表面的自相关函数为

(3)
式中:M,N----分别为x,y方向的采样点数,通常取M=N,采样间隔也取相同值。
根据维纳-辛钦定理,在此基础上提出一种基于Fourier变换的功率谱密度方法。功率谱密度是对粗糙表面进行全面描述的一种函数。粗糙表面形态可以看作是不同频率下的正弦或余弦波之和,则功率谱密度是在Fourier空间中粗糙度状态的整体频率成分构成。
功率谱密度函数与自相关函数是一对傅里叶变换对。文中将非归一化的自相关函数C(Δx,Δy)做Fourier变换,获得表面轮廓的功率谱密度函数。
若粗糙表面随机,且高度服从高斯分布,入射光线垂直于光学表面时,散射表面传递函数为

(4)
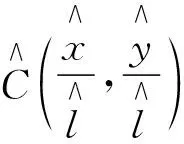
式中:l----自相关函数的相关长度;
λ----入射光波长;
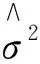
作傅里叶逆变换,即可得到点扩散函数,其公式为
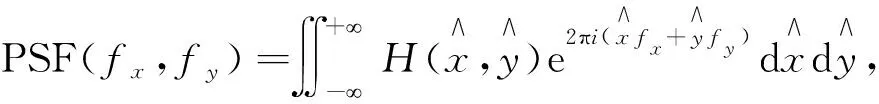
(5)
式中:PSF----点扩散函数。
2 仿真分析
以复曲面作为目标光学自由曲面,应用Matlab软件对其进行椭圆振动切削加工表面形貌仿真分析和加工表面的光散射分析。复曲面的数学表达式为
z=Rb-

(6)
其中
Rb=d1+d2,Rc=d1,
式中:d1----圆环回转半径;
d2----圆环半径。
采用麻省理工学院Ludwick加工眼科透镜时使用的数据,Rb=265 mm,Rc=132.5 mm。
三维复曲面在加工坐标系中的示意图如图 3所示。
椭圆振动车削仿真加工参数见表 1。

表1 椭圆振动车削仿真加工参数
以复曲面为例,对复曲面进行椭圆振动车削刀具轨迹规划,刀位点路径与复曲面三维对比结果如图 4所示。
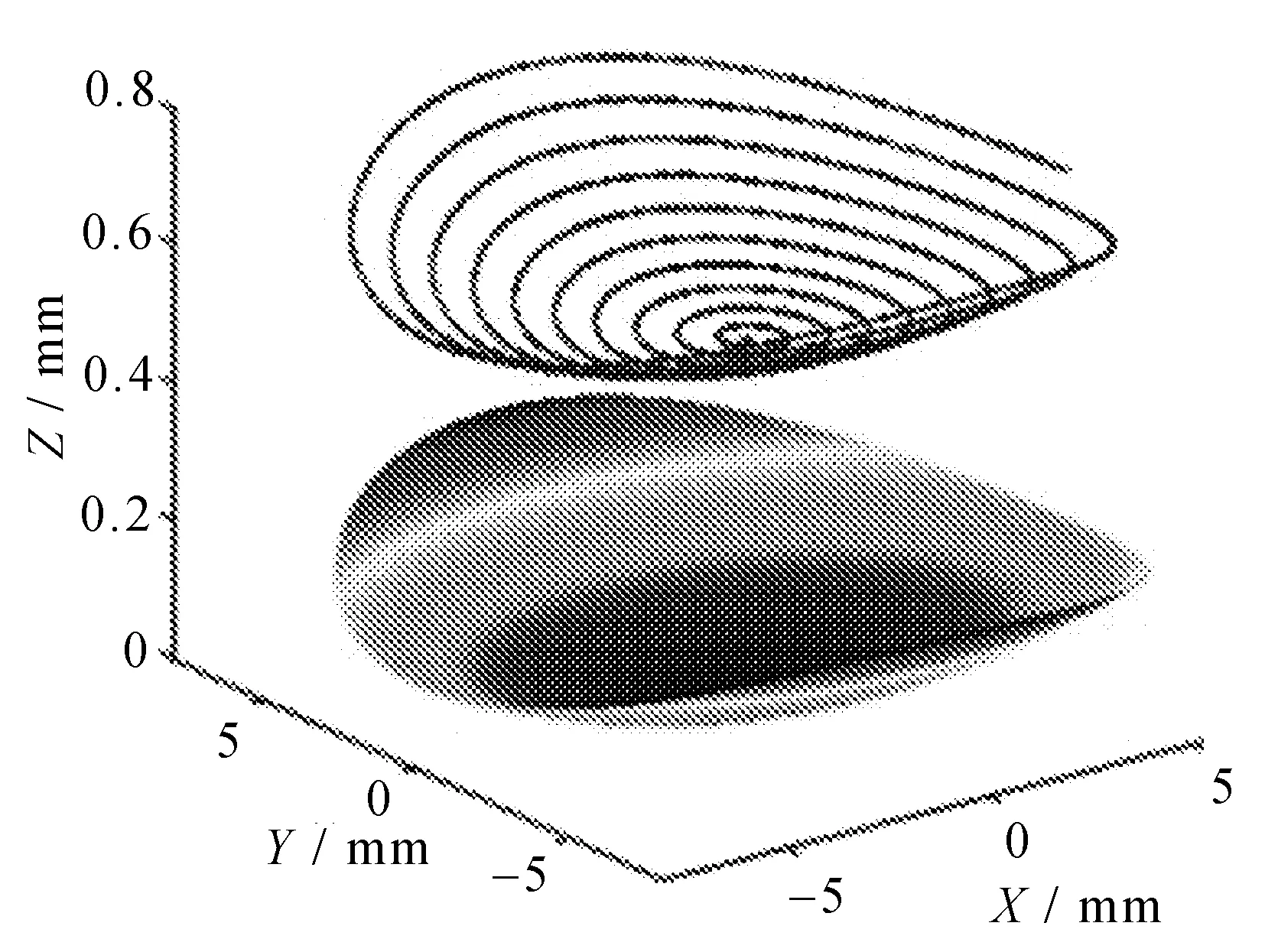
图4 刀位点路径与复曲面三维对比
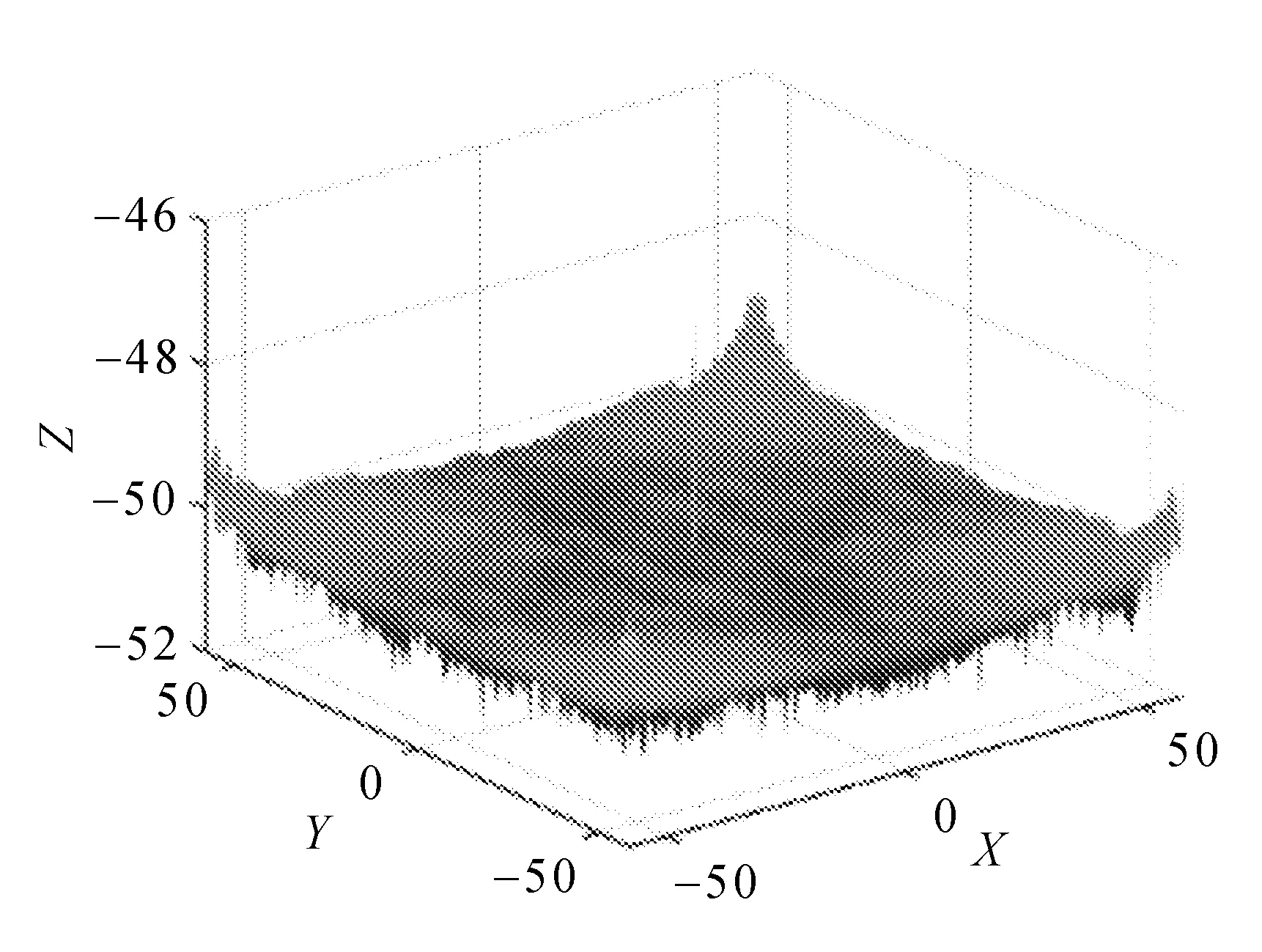
当进给量为0.1 mm/r,刀尖圆弧半径为0.1 mm时,让刀具的走刀轨迹对加工表面进行刻划复映,基于快速刀具伺服金刚石切削过程中的表面形貌模型算法[19],通过计算可以得到三维椭圆振动切削光学自由曲面的残高形貌模型,如图 5所示。
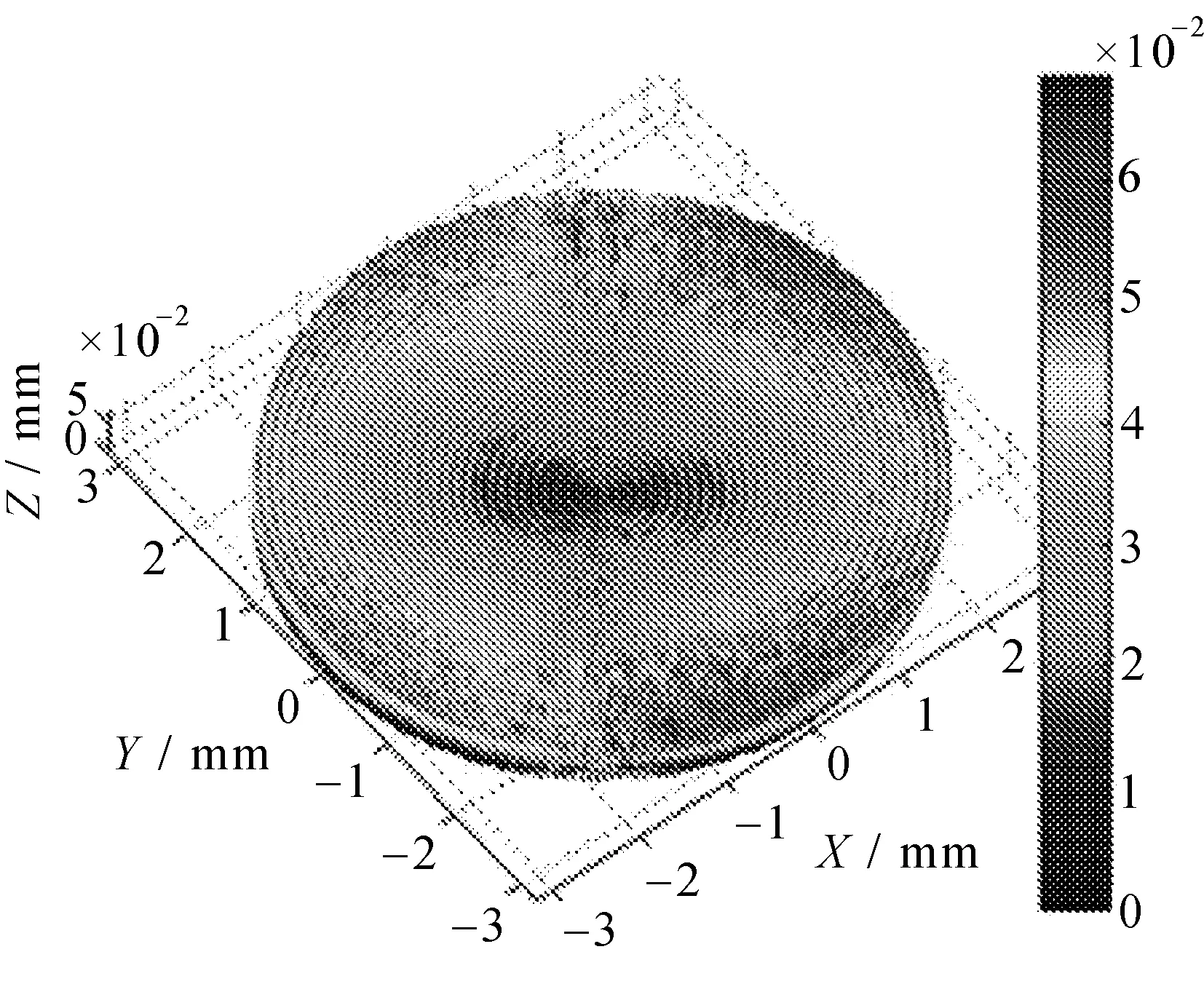
图5 复曲面残高形貌立体图
在三维椭圆振动车削加工光学自由曲面过程中,加工参数的选取数值会对光学产品的表面质量和它的光学性能产生一定的影响。通过研究加工参数与表面粗糙度和光散射的相互关系,可以为选择合理的加工参数进行加工提供一定的指导价值。文中以加工参数中的进给量和刀尖圆弧半径作为自变量,以Sq值作为目标函数研究加工参数对表面粗糙度的影响,以加工表面轮廓的点扩散函数作为目标函数研究加工参数对光散射的影响。
分析过程中,采用进给量和刀尖圆弧半径参数见表 2。

表2 三维评价用切削条件
2.1 复曲面加工表面粗糙度分析
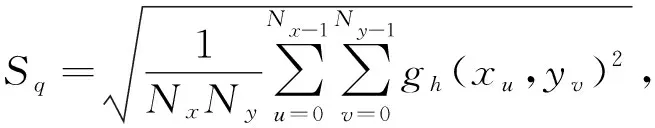
(7)
式中:Nx,Ny----分别为x,y方向点的个数;
u,v----表面残高形貌仿真区域变量,u=0,1,2,…,Nx-1,v=0,1,2,…,Ny-1;
(xu,yv)----仿真区域中第(u,v)个点的坐标;
gh(·,·)----三维表面残高形貌函数。
基于快速刀具伺服金刚石切削过程中的表面形貌模型算法[19],通过计算可以得到三维椭圆振动切削光学自由曲面的残高形貌模型,然后根据式(7)获得加工表面的粗糙度值。
当进给量作为自变量时,对三维椭圆振动车削加工复曲面进行三维表面形貌分析,计算得到的表面均方根偏差Sq值见表3。
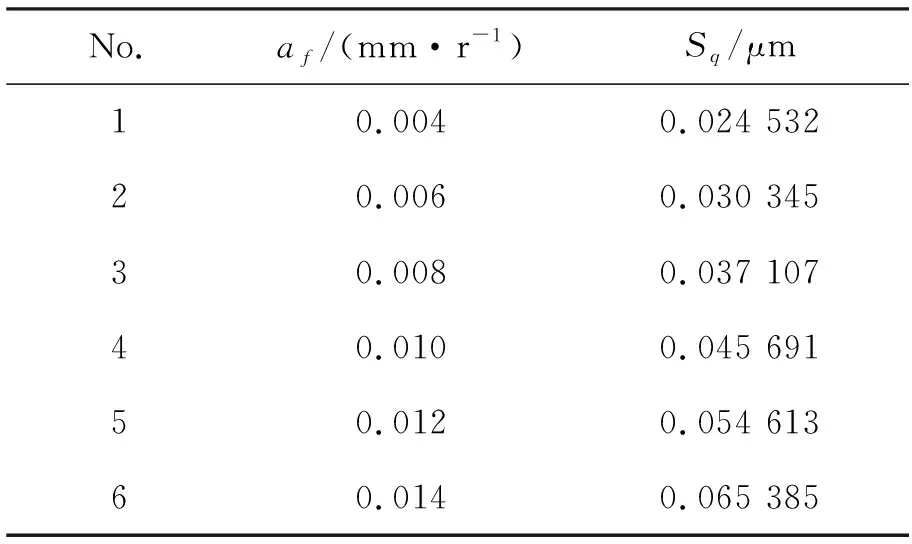
表3 不同进给量对应的表面粗糙度值
从表中可以看出,进给量对三维椭圆振动切削复曲面的表面粗糙度产生了影响,根据表3数据得到不同进给量对表面粗糙度的影响规律曲线,如图 6所示。
从图中可以看出,进给量对三维椭圆振动切削复曲面的表面粗糙度影响呈现规律性,表面粗糙度随着进给量的增加而增加,即进给量的增加降低了表面质量。因此,为获得较好的加工表面,可以尽可能选择较小的进给量。可以看出,在同等条件下,进给量为0.004 mm/r时,表面粗糙度值最小。

图6 不同进给量对表面粗糙度影响曲线
当刀尖圆弧半径作为自变量时,对三维椭圆振动车削加工复曲面进行三维表面形貌分析,不同刀尖圆弧半径对应的表面粗糙度值见表4。
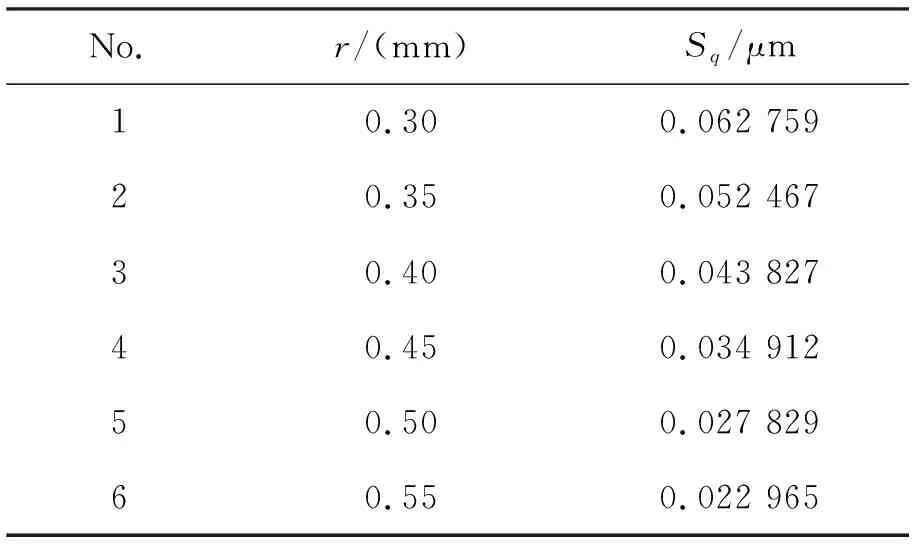
表4 不同刀尖圆弧半径对应的表面粗糙度值
从表中可以看出,刀尖圆弧半径对三维椭圆振动切削复曲面的表面粗糙度产生了影响,根据表4数据得到不同刀尖圆弧半径对表面粗糙度的影响规律曲线,如图 7所示。
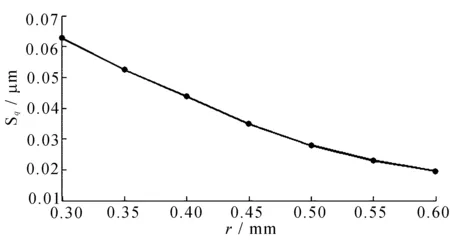
图7 不同刀尖圆弧半径对表面粗糙度影响曲线
从图中可以看出,刀尖圆弧半径对三维椭圆振动切削复曲面表面粗糙度的影响呈现规律性,表面粗糙度随着刀尖圆弧半径的增大而减小,即刀尖圆弧半径的增加提高了表面质量。因此,为获得较好的加工表面,在不发生干涉情况下,尽可能选择较大的刀尖圆弧半径。可以看出,在同等条件下,刀尖圆弧半径为0.60 mm 时,表面粗糙度值最小。
2.2 加工粗糙表面光散射分析
根据高斯滤波的原理,对前述应用Matlab软件仿真获得的椭圆振动车削加工复曲面的三维表面形貌进行重构,获得只含有粗糙度误差的表面形貌数据。文中在Harvey-Shack散射理论的基础上,采用表面散射传递函数对应的点扩散函数研究不同进给量和不同刀尖圆弧半径条件下仿真加工获得的粗糙复曲面的光散射特性。
在进给量作为自变量的情况下,对应的点扩散函数图如图8所示。

(a) af=0.004 mm/r
从图中可以发现,随着进给量的增大,点扩散函数图也发生了相应的变化,这些变化可以归纳为以下几点:
1)随着粗糙度的增加,圆心处的光晕也随之增加,表明粗糙度越高,能量损耗就越大。
2)当表面粗糙度增加时,点扩散曲线的中心位置会随进料速度的增加而改变。
3)中心点附近的晕圈数目随表面粗糙程度的增加而增加。
4)点扩散函数随粗糙度值的增加而变得模糊。
①随着进给量的增加,点扩散函数图逐渐变模糊。
②由于表面粗糙度的存在,中心点处的能量减小,且转移到中心点的周围。随着进给量的增加,点扩散函数图四周的晕圈数量逐渐增多,并且逐渐变亮,即进给量的增加导致光学元件加工表面粗糙度的增加,进而致使中心点的能量损失增加。所以进给量的增加将导致光散射掉的能量增加,对光学元件的光学性能产生坏的影响。
③随着进给量的增大,点扩散函数的图形不断发生变化。点扩散函数图的中心部分随着进给量的变化逐渐变化。在进给量由0.004 mm/r增加至0.006 mm/r,即进给量刚开始增加的时候,点扩散函数图中心部分的变化程度是最小的;在进给量由0.012 mm/r增加至0.014 mm/r时,点扩散函数图中心部分的变化程度达到最大。
④随着进给量的增加,点扩散函数图中心部分的变化速率是逐渐增加的。但是在图6的曲线图中,表面形貌均方根偏差Sq随进给量而变化的变化速率是近似恒定不变的,或者说相对于点扩散函数中心部分的变化速率小得很多,可以近似看作是不变的。由此可以得出,在一定条件下,因为进给量的改变而引起表面粗糙度的改变,当粗糙度在一定范围内变化时,其对于光学元件光学性能的影响程度较小,即进给量在该范围内变化,产生的主要加工误差不是粗糙度,而是波纹度或者面形误差。该结论与向阳等[20]在其论著中得出的结论相近,说明文中研究具有一定程度上的正确性。
在刀尖圆弧半径作为自变量的情况下,对应的点扩散函数图如图9所示。
从图中可以发现,随着刀尖圆弧半径的增大,点扩散函数图也发生了相应的变化,这些变化可以总结为以下几个方面:
1)当表面粗糙度降低时,圆心附近的光晕会逐渐暗淡,表明粗糙度愈低,能量损耗愈小。
2)当表面粗糙度降低时,曲线中心区域会随刀具圆弧半径的增大而改变。
3)中心点附近的晕圈数目随粗糙度的降低而降低。
4)随着表面粗糙度的减小,点扩散函数图逐渐变清晰。
(a) r=0.30 mm
①随着刀尖圆弧半径的增加,点扩散函数图的变化相比于进给量的增加而引起的点扩散函数图的变化有着相反的影响,即刀尖圆弧半径的增加,将导致光学元件加工表面质量变好,光散射掉的能量减小,对光学元件的光学性能产生好的影响。
②从图6和图7可以看出,在一定条件下,表面轮廓均方根偏差随进给量和刀尖圆弧半径的变化而变化,变化速率是相似的,只是符号差别。从点扩散函数图的清晰度来看,对比进给量对点扩散函数图产生的影响可以发现,刀尖圆弧半径的增加引起的点扩散函数图的变化速率是不明显的。由此推断,在一定条件下,刀尖圆弧半径和进给量的改变对加工表面质量的影响程度是一致的,但是对于光学元件光学性能的影响程度是不同的,由于进给量的改变而引起的光学元件光学性能的变化速率要小于进给量引起的光学元件光学性能的变化速率(由于刀尖圆弧半径的改变而对光学元件光学性能产生的影响程度要小于进给量的变化产生的)。
3 结 语
以椭圆振动车削加工复曲面为例,分析了加工参数对自由曲面光学元件表面质量和光散射的影响规律。研究表明,随着进给量的增大和刀尖圆弧半径的减小,复曲面的表面粗糙度值会增大,粗糙表面的点扩散函数会减小。但刀尖圆弧半径的变化对光学元件光学性能的影响小于进给量的改变。因此,在实际加工过程中,不仅从表面粗糙度的角度,还要从光学性能的角度为光学自由曲面的高效高精度加工寻找合理的加工参数。
