基于动态矩阵的未知环境地图构建与路径规划*

张志远，陈海进

(南通大学信息科学技术学院，江苏 南通 226019)

1 引言

目前，扫地机器人路径覆盖算法有很多，早期的随机覆盖式[1]算法容易实现并且对于机器人硬件设备要求低，但在复杂的环境中不一定能实现全覆盖，路径重复率相当高。后来研究人员提出了启发式规划算法[2，3]和螺旋生成树覆盖算法[4-6]，虽然实现了路径的全覆盖，但是栅格地图的构建[7-10]和区域划分的过程繁琐，路径重复率较高。为解决这个问题研究人员又提出了Boustrophedon局部覆盖算法[11]，该算法通过牛耕式运动将整个地图动态划分为若干子区域，每个子区域内部通过牛耕式往返完成简单覆盖，再利用深度优先搜索遍历各个子区域，从而实现全覆盖。该算法划分出的子区域数量较多，回溯路径重复率较高。上述算法都是在地图信息完全已知或部分已知的前提下(需向机器人输入地图的边界大小)再规划覆盖路线的。

本文提出的基于动态矩阵的未知环境地图构建算法，利用机器人测距传感器[12]的数值与当前位置坐标的数学关系，建立不断扩张的二维动态矩阵，借助标记回溯法[13，14]实现全覆盖地图探测。完成地图构建后，本文提出基于封闭区域检测的路径规划算法，在路径规划中优先处理检测到的封闭区域，在封闭区域内采用沿边循迹与牛耕式运动相结合的子区域路径规划方式。通过仿真验证,本文提出的基于封闭区域检测的路径规划算法与传统的局部覆盖算法相比，在减少子区域数目、回溯路径总长和路径重复率等指标上有明显提高。

2 相关算法

2.1 A*算法

A*算法[15-18]是在二维静态网格中规划最短路径的较为有效的算法。算法规定，从起点开始每移动1个栅格都需要对当前位置周围8个栅格进行计算筛选，依次计算8个栅格相对于当前栅格位置的估计函数值f(s)，其计算如式(1)～式(3)所示:

f(s)=g(s)+h(s)

(1)

(2)

h(s)=|xs-xg|+|ys-yg|

(3)

其中,c为起点栅格，s为当前选中栅格，g为终点栅格，(xc,yc)为起点栅格的坐标，(xs,ys)为当前选中栅格的坐标，(xg,yg)为终点栅格的坐标，g(s)为当前选中栅格到起点栅格的欧氏距离，h(s)为当前选中栅格到终点栅格的曼哈顿距离。通过依次计算，选取8个相邻栅格中f(s)值最小的栅格作为下一个目标栅格，因此可以通过A*算法规划出一条死点(四周栅格均为障碍或已清扫点)到回溯点[12]的最短回溯路径。

2.2 Boustrophedon局部覆盖

Boustrophedon局部覆盖是一种基于回溯的覆盖算法，该算法要求提前给机器人输入需要清扫的地图模型边界条件，用固定的运动模式(比如牛耕式)让机器人在清扫的过程中划分区域，将当前地图模型中已清扫路径和边界与未清扫区域构成的封闭区域筛选出来作为划分的子区域，划分出子区域后并不立即处理，继续执行清扫命令，不断划分出新的子区域，直至机器人运动至死点后才开始处理剩余的各个子区域，通过深度优先搜索DFS，规划出一条遍历所有子区域的回溯路径，直至每个子区域都被清扫完毕。如图1所示，斜线填充区域即为机器人通过已清扫路径分割出的子区域。黑色箭头实线为机器人清扫遍历路径，灰色箭头实线为机器人往返各个子区域之间的回溯重复路径。

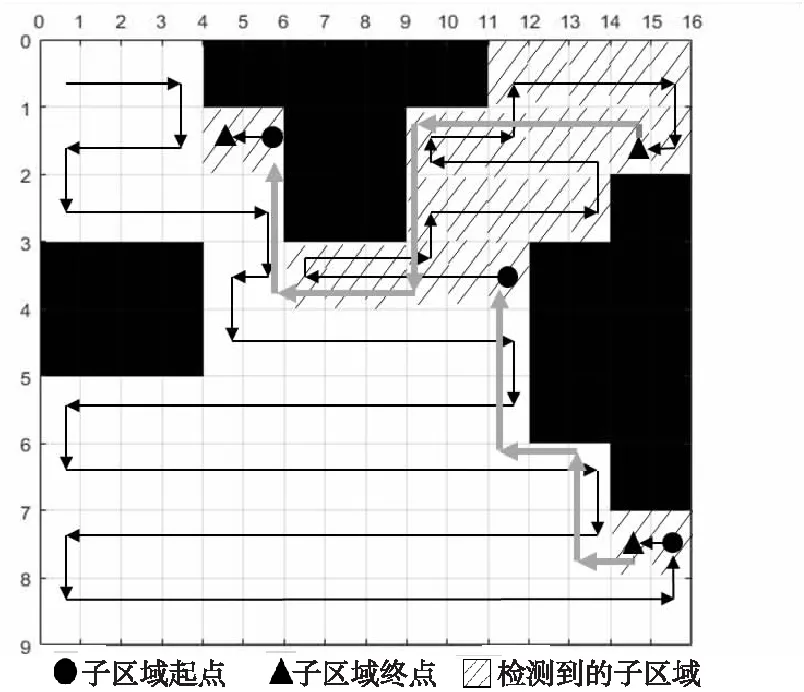
Figure 1 Boustrophedon local coverage algorithm

通过上述分析不难看出，Boustrophedon局部覆盖算法容易实现，路径规划简单，但是分割出的子区域较多，分割出子区域但并不优先处理，区域内路径规划方式单一，种种问题造成了子区域之间连通往返的重复路径较多，清扫效率较低。

3 基于动态矩阵的未知环境地图构建算法

3.1 机器人基本运动机制

本文规定机器人以牛耕式运动轨迹交替往复清扫，设置运动方向优先级为:东>西>北>南。每当清扫过程中遇见障碍物时，机器人根据运动方向优先级，原地旋转90°转向下一个优先级方向。

3.2 回溯机制

3.2.1 回溯点列表的建立

机器人按基本运动机制清扫时，很容易进入运动死点。这时需要建立一套完整的回溯[10]机制帮助机器人脱离死点。在Boustrophedon局部覆盖算法中，机器人的运动回溯点通常设置为未清扫区域的边角点，而边角点的位置信息需要在地图的边界条件已知的前提下才能获取。

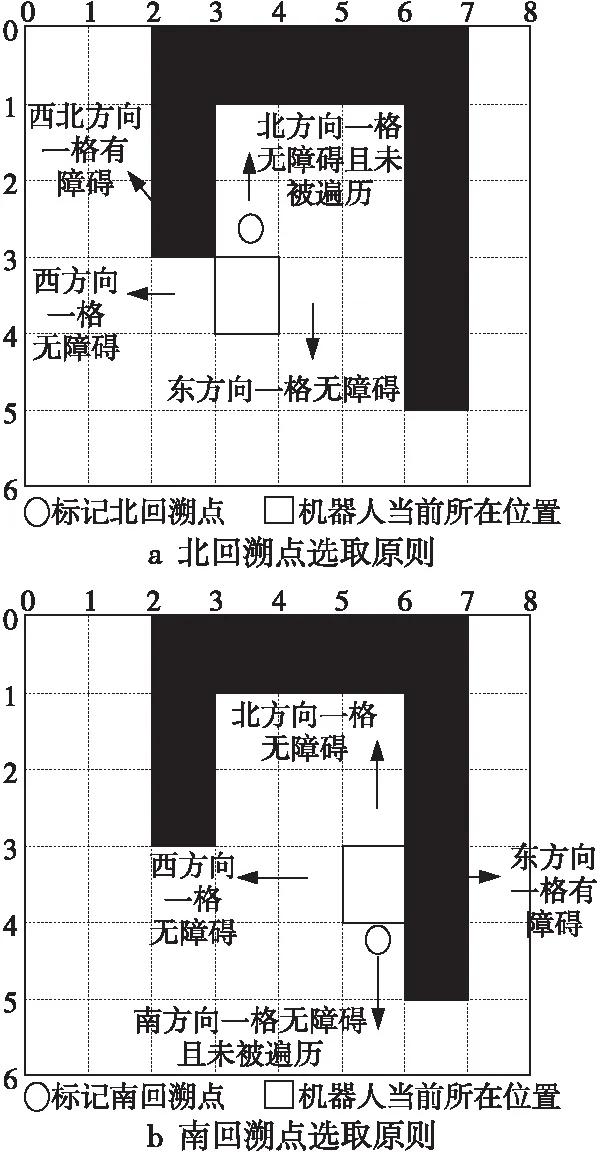
Figure 2 Schematic diagram of mark backtracking algorithm

本文基于动态矩阵的未知环境地图构建算法在地图环境完全未知的前提下采用标记回溯法设置回溯点，规定如下:若前进方向与北方向均无障碍且未被遍历，根据运动方向优先级(东>西>北>南)，机器人优先向前进方向(东或西)运动探测，所以北方向存在尚未被遍历探测的空间，需要一个北回溯点来回溯遍历探测这些栅格空间。如图2a所示，当前进方向与北方向一格均无障碍且未被遍历，而东北或西北方向一格存在障碍时，本文选取当前位置北方向一格的点作为标记的北回溯点，依据这个原则选取的回溯点通常为北方向未被探测空间的边角点，南回溯点选取原则与北回溯点相似，如图2b所示。这样，即使未知地图边界条件，也可以设置未清扫区域边角点作为回溯点，从而建立回溯点列表。

3.2.2 回溯点选取原则

标记回溯算法规定回溯点选取优先级:北回溯点>南回溯点。每当机器人按基本运动机制运动至死点时，立即检测回溯点列表中是否存在北回溯点，若存在，计算各北回溯点与死点之间的欧氏距离，如式(4)和式(5)所示:

i∈{A,B,…,N}

(4)

S=min(SA,SB,…,SN)

(5)

其中，(Xi,Yi)为由点A到点N组成的回溯点列表中的某个待选回溯点，(Xdp,Ydp)为死点。遍历回溯点列表，选取欧氏距离最小的点回溯,并利用A*算法规划回溯路线[8-12]。若回溯点列表中不存在北回溯点进而选择南回溯点回溯。若列表中南、北回溯点个数均为0，则机器人移动至最近未清扫栅格处。

在实际探测过程中，回溯列表中的每个回溯点不可能都被回溯，一旦有回溯点被遍历，将其自动删除，释放内存空间，提高程序运行效率。

如图3所示为部分探测路径图，起点为原点(0,0)，黑色实线为探测路径轨迹，A点和B点均为机器人运动过程中标记的北回溯点，C点为标记的南回溯点，当机器人第一次进入死点1时:

S=min(SA,SB)=SA

(6)

故选取A点回溯，并利用A*算法规划回溯路径，到达A点后从回溯列表中删除该点。B点在到达A点之后的探测路径中会被遍历，故B点被删除。利用A*算法规划的回溯路径如图3中灰色实线箭头所示，进入死点2后由于北回溯点列表中已不存在回溯点，故选取南回溯点列表中的节点进行回溯(图3中的C点)，加粗黑色实线为寻路轨迹。

Figure 3 Path map using mark backtracking algorithm

3.3 动态矩阵地图构建

主流的基于激光即时定位与地图构建SLAM(Simultaneous Localization And Mapping)的地图构建方法在初次获取地图信息时并不能满足扫地机器人全覆盖清扫的要求，同时需要通过人机交互平台完成对机器人的移动控制。由于机器人的移动轨迹和位姿的不确定性，因此需要在机器人的工作环境中布置人工信标，以达到定位和精准构图的目的，虽然构建地图清晰精准，但对于多变陌生环境，需要投入的人工也随之上升。本文基于动态矩阵的未知环境地图构建算法在二维栅格建模的基础上采用动态矩阵的模型，利用机器人移动轨迹始终为南北垂直的牛耕式路径这一特点，较容易获取机器人在当前动态矩阵中的坐标，利用机器人当前位置坐标与传感器返回动态数据的数学关系完成动态矩阵的扩展，进而实现对陌生环境的地图构建。本文基于动态矩阵的未知环境地图构建算法在陌生多变的环境中尽可能降低了人工成本，在构建地图的同时，实现了初次清扫的全覆盖。

机器人接收东、西、南、北4个方向传感器的环境数据，得到机器人与周围障碍或边界的4个方向距离，分别记为Ey、Wy、Sx、Nx。以初始矩阵的西北角为坐标原点，设X为生成的二维动态矩阵宽度，Y为生成的二维动态矩阵长度，定义正东方向为Y轴正方向，正南方向为X轴正方向，可以得到:

X=Nx+Sx-1

(7)

Y=Ey+Wy-1

(8)

基于动态矩阵的未知环境地图构建算法流程如下所示:

(1)矩阵的建立。

以Y和X为长和宽生成二维栅格矩阵，并以机器人直径为单位进行单元格划分，记录机器人位置在当前矩阵中的坐标，机器人每移动1个栅格，坐标相应改变，记机器人动态坐标为(y,x)。

(2)动态矩阵参数记录。

机器人按基本运动机制运动，同时记录机器人当前所在行每一个传感器探测到的Nx和Sx的数值生成line列表，机器人清扫过多少行就生成相应个数的line列表，并把每一个line列表中的Nx和Sx最大值分别记为Nxmax和Sxmax。

(3)动态矩阵的扩展。

红外、激光雷达和超声波等传感器均可作为构建动态矩阵时所用的传感设备。考虑到不同种类传感器测距范围的差异，部分情况下某一方向障碍物或边界与机器人的距离可能超出传感器的测距范围，此时传感器的返回值为其最大测距值。因此，基于动态矩阵的未知环境地图构建算法规定，在机器人遇到障碍物或运动至矩阵边界位置时进行扩展检测，以应对传感器测距范围受限的情形。

①矩阵宽度扩展。

当机器人遇障碍(Ey=0或Wy=0)或运动至当前动态矩阵边界处(当前位置坐标x=1或x=X)时均需进行扩展检测，检测记录机器人传感器数据的line列表(假设为第n个),若第n个line列表的Nxmax>x(x为机器人当前纵坐标的值)，说明动态矩阵需在原矩阵的基础上向北扩展Nxmax-X(X为动态矩阵当前宽度)个单位，动态矩阵宽度X相应改变；若Sxmax>(X-x),说明进入下一行后动态矩阵还需在原矩阵的基础上向南扩展Sxmax-(X-x)个单位，X值再次相应改变。机器人当前位置坐标也随矩阵扩展相应改变。

②矩阵长度扩展。

若机器人遇障碍(Ey=0或Wy=0),进入下一行清扫后(假设从第n行进入第n+1行)读取当前所在位置数据Wyn+1和Eyn+1。若Wyn+1>y,说明进入下一行后动态矩阵需在原矩阵的基础上向西扩展Wyn+1-y个单位，动态矩阵长度Y相应改变;若当前位置Eyn+1>Y-y,说明进入下一行后动态矩阵需在原矩阵基础上向东扩展Eyn+1-(Y-y)个单位，Y值再次相应改变，机器人当前位置坐标也随矩阵扩展相应改变。

若机器人运动至当前动态矩阵边界处(当前位置坐标y=Y或y=1)，当机器人运动至矩阵东边界(y=Y)时,若Eyn>0,动态矩阵需在原基础上扩展Eyn个单位，动态矩阵长度Y相应改变。当机器人运动至矩阵西边界(y=1)时，若Wyn>0,动态矩阵需在原基础上扩展Wyn个单位，动态矩阵长度Y相应改变。

(4)回溯。

当机器人按基本运动机制运动至死点位置时，从回溯点列表中选取最近回溯点回溯，返回步骤(1)执行操作命令，若回溯点列表中回溯点个数为0且当前动态矩阵中不存在未被遍历的栅格，则表示地图信息已全覆盖采集，结束循环。基于动态矩阵的未知环境地图构建算法流程图如图4所示。

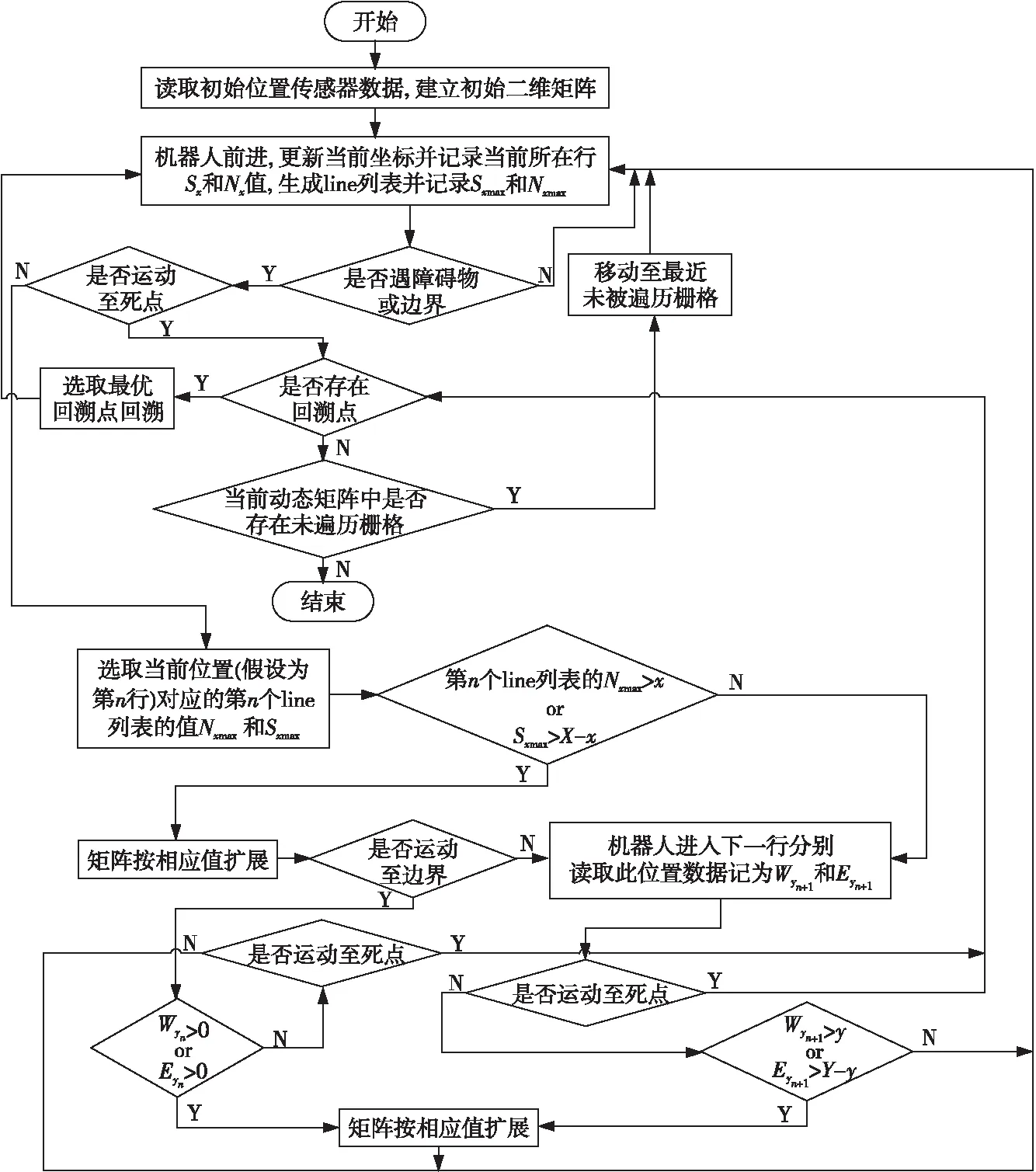
Figure 4 Flow chart of unknown environment map construction algorithm based on dynamic matrix

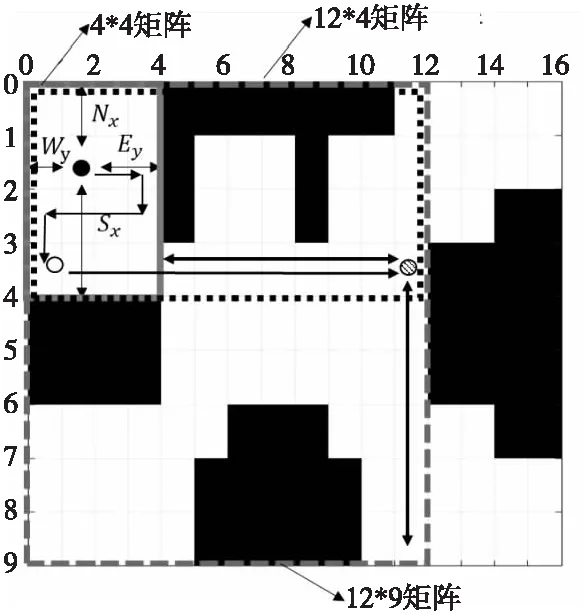
Figure 5 Extended schematic diagram of unknown environment map construction algorithm based on dynamic matrix

动态矩阵扩展实例如图5所示，黑色实心圆点为机器人起始点，在该点处根据传感器数值建立初始4*4矩阵(如图5中灰色实线框所示)，机器人按牛耕式轨迹运动至坐标为(1,3)的栅格处，西侧遇障碍物(Wy=0)，原地旋转90°运动至下一行的(1,4)栅格,至黑色空心圆点进行扩展检测。获取当前机器人传感器数据Ey4(第4行),Ey4=12，判定Ey4>(Y-y)，故矩阵向东扩展Ey4-(Y-y)=8个单位，生成12*4矩阵(如图5中黑色点虚线框所示),同时矩阵长度Y更新为12。机器人运动至(4,12)黑色阴影底纹圆点所在栅格处时，东侧遇障碍物(Ey=0)，此时判定第4个line列表的Sxmax>X-x,故矩阵需向南方向扩展Sxmax-(X-x)=5个单位，生成12*9矩阵(如图5中黑色短横虚线框所示)，同时矩阵宽度更新为9。

4 路径规划

为了解决Boustrophedon局部覆盖算法子区域间连通产生的重复路径问题，本文对其进行了优化，优先处理检测到的封闭区域，并改进了封闭区域内的路径规划方式。本文提出的基于封闭区域检测的路径规划算法规定东、西方向清扫优先，按牛耕式运动轨迹遍历清扫，清扫的同时检测已经过路径是否与已知地图中的障碍物或边界构成封闭区域，若检测到区域封闭，设置当前所在位置为起始点，封闭区域底端点为终点，沿区域边界循迹至区域终点，到达终点后再由该点出发按牛耕式轨迹清扫返回至区域起始点的位置，从而实现对整个封闭区域的全覆盖清扫。

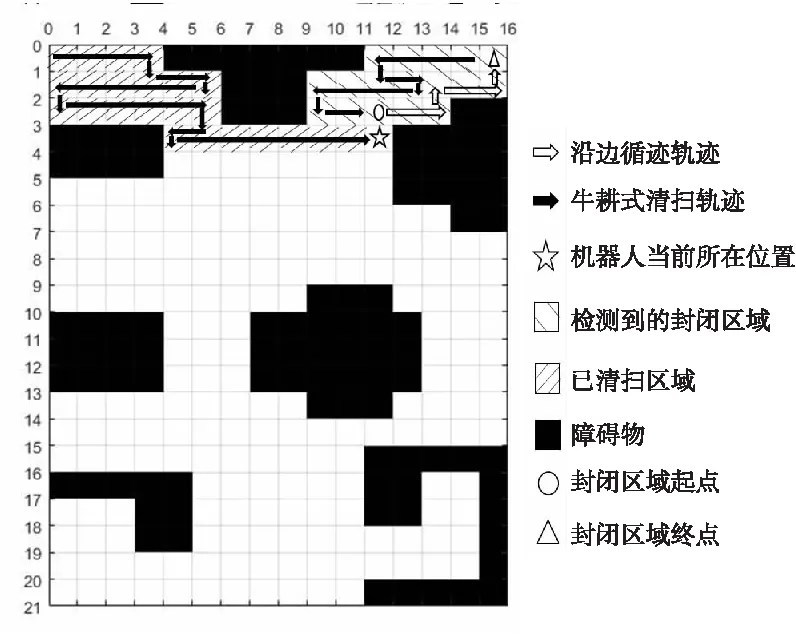
Figure 6 Path planning algorithm based on closed area detection

图6是对基于封闭区域检测的路径规划算法的描述。通过上述分析可以看出，不同于Boustrophedon局部覆盖算法，本文提出的基于封闭区域检测的路径规划算法进行覆盖时，一旦产生由已知路径与障碍物或边界构成的封闭区域便会优先处理该区域，这样就减少了子区域间连通带来的区域间往返路径的重复清扫。传统子区域内的路径规划从子区域起始点出发，按牛耕式遍历至区域底端，完成区域全覆盖清扫，之后再回溯至起始点，这就产生了不必要的由底端终点返回至区域起始点的纵向回溯路径。封闭区域检测算法采用沿边循迹与牛耕式运动相结合的路径规划方法，让机器人优先沿区域边界循迹至区域底端，再由底端出发进行牛耕式遍历清扫，清扫的同时重新返回至起始点位置，这样避免了不必要的起终点纵向回溯路径，减少了回溯次数，缩短了回溯路径，重复覆盖率明显降低，提高了算法的整体性能。

5 算法评估

5.1 路径规划算法仿真结果对比

通过前文的对比可知，本文提出的基于封闭区域检测的路径规划算法与Boustrophedon局部覆盖算法[4,5]都是利用运动轨迹对地图区域进行分解划分的，但它们对于分解区域的处理方式以及区域内部路径规划方式有所不同。

本节对室内环境模型按照由简单到复杂的顺序，利用Matlab仿真平台进行对比实验。图7是本文基于封闭区域检测的路径规划算法和Boustrophedon局部覆盖算法对室内环境模型的仿真结果对比。

对应图7右侧图注所示，斜条纹栅格表示机器人第1次遍历的区域，灰色栅格表示机器人第2次遍历的区域，斑马点纹栅格示机器人第3次遍历的区域。算法性能的4个评价指标为：子区域个数、回溯路径总长、初始覆盖率和路径重复率，2种算法的仿真结果统计如表1所示。

Figure 7 Simulation results comparison

Table 1 Simulation results analysis of path planning

5.2 基于动态矩阵的未知环境地图构建算法仿真结果

为了验证基于动态矩阵的未知环境地图构建算法的可行性，本节使用Webots平台进行仿真实验。在理想三维空间模型中，设置地图尺寸为400 cm*400 cm的规则矩形，机器人直径为33 cm，默认其为1个栅格大小。机器人配备4个红外测距传感器，测距范围为0～200 cm，误差范围为0～2 cm。机器人运动执行机构为4轮马达旋转电机，可通过差速控制各个电机实现原地转弯的基本功能。

在室内环境中以本文基于动态矩阵的未知环境地图构建算法构图和清扫的过程如图8所示，黑色实线为机器人牛耕式运动轨迹，灰色实线为机器人回溯轨迹。图中A、B分别为探测过程中标记的回溯点，①、②、③、④标号点为机器人遇障碍物进行地图扩展检测的位置，其探测获得的矩阵分别为：5*7矩阵，11*7矩阵，11*12矩阵，12*12矩阵。机器人以地图左上角位置为起点，自北向南以牛耕式运动清扫探测，运动至地图右下角的死点处选取标记的回溯点A进行回溯，到达A点完成子区域的清扫探测后，检测矩阵中已无回溯点和未清扫点，探测结束，在构建地图的同时完成全覆盖清扫。

Figure 8 Simulation diagram of unknown environment map construction algorithm based on dynamic matrix in three-dimensional model

6 结束语

本文基于动态矩阵的未知环境地图构建算法可以适应复杂陌生环境，有效提高机器人的自主性，降低人工代价。本文提出的基于封闭区域检测的路径规划算法，优先处理由已清扫路径、障碍物和边界构成的封闭区域，一定程度上避免了子区域间的回溯路径，故而不存在3次重复清扫的栅格。算法在封闭区域内采用沿边循迹和牛耕式运动相结合的路径规划方法，减少了子区域内纵向的回溯路径，有效降低了重复率。由实验数据可以看出，室内环境越复杂，本文提出的基于封闭区域检测的路径规划算法相对于Boustrophedon算法的优势就越明显，应变性能越强。