一类带Neumann边界波动方程的稳定性

郭春丽

(四川文理学院 数学学院,四川 达州 635000)

0 前 言

众多的自然现象和实际问题都可以由偏微分方程来描述,比如扩散、热传导等物理现象可以由反应扩散方程来描述,又比如波的传播与衰减、弹性体的平衡和振动都能由波动方程来表达,还有原子核与电子的相互作用、化学反应过程、流体的运动、电磁相互作用等自然现象的基本规律都可以写成偏微分方程的形式.[1]由于偏微分方程在实际中应用广泛,人们对其了解得越来越多、越来越深入,形成了数学中一门重要的分支—偏微分方程理论,其中,偏微分方程的控制问题吸引了大批学者对其进行研究.[2-9]

偏微分方程控制研究包括能稳性、能控性、反馈控制器的设计等方面,在偏微分方程的边界反馈控制器设计时,常见方法有damping 法、Backstepping 方法、Lyapunov 函数法等,其中Backstepping 方法突破了求解过程过于复杂的局限性,因此,近年来被广泛应用于偏微分方程的边界反馈控制器的设计中.[3-9]文献[4-5]讨论了反应扩散方程的稳定性,文献[6-7]考虑了波动方程的稳定性,文献[8-9]涉及偏微分方程与常微分方程级联系统的稳定性. 下面将运用Backstepping 方法讨论一类带Neumann 边界波动方程的稳定性,并设计出该方程的边界反馈控制器.

1 问题陈述

考虑带Neumann 边界一维波动方程控制系统:

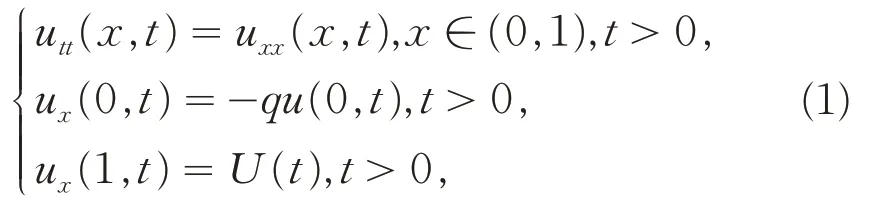
其中,q≥1,u(x,t)表示弦上各点在t时刻沿垂直于x方向的位移,U(t)是反馈控制器. 此控制系统(1)在u(1,t) = 0 时,即不加控制时控制系统(1)是不稳定的.

2 控制器的设计

为了设计控制系统(1)的反馈控制器,选用Backstepping 方法进行设计,该方法的设计思路是利用可逆变换将控制系统(1)转化为稳定的目标系统,再利用变换的有界性和目标系统的稳定性证明控制系统的稳定性.

首先,选定如下的系统作为目标系统:

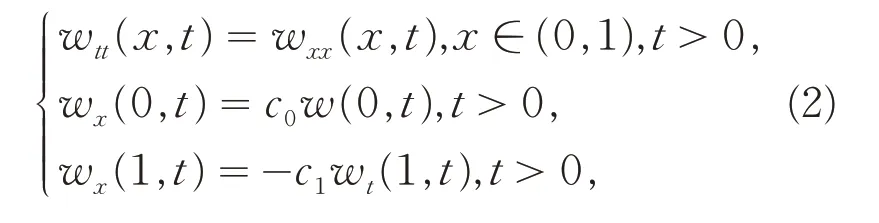
其中,c0> 0,c1> 0. 目标系统(1)是指数稳定的.[3]

其次,引入Voltegral变换:

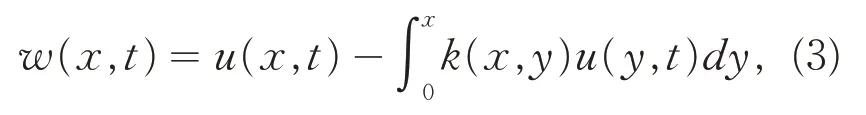
其中,k(x,y)是待定的核函数.[6-7]变换(3)将控制系统(1)转化为目标系统(2).

然后,在变换(3)的两边分别关于变量x和t求偏导,从而有:

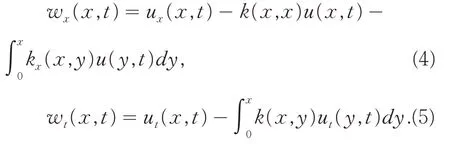
在(4)式中,令x= 1,再由(5)式及系统(1)和(2)中的边界条件可得:

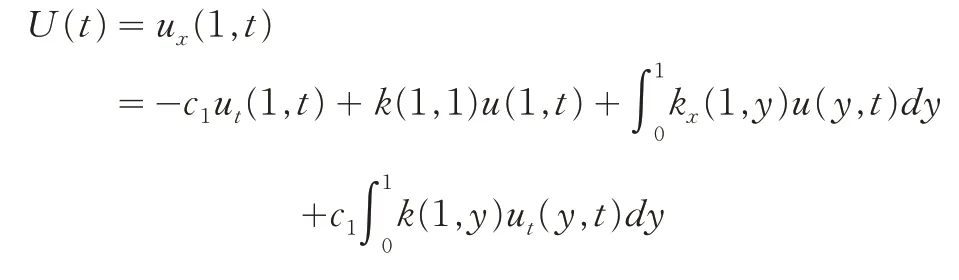
最后,为了证明控制系统(1)在反馈控制器(6)下是稳定的,需要得到变换(3)的逆变换,再利用目标系统的稳定性得到控制系统的稳定性,从而验证反馈控制器的有效性.

3 核函数的计算

本节将求解出变换(2)中的核函数k(x,y),从而得到反馈控制器(6).

首先,在(4)式的两边同时关于变量x求偏导数,得到:

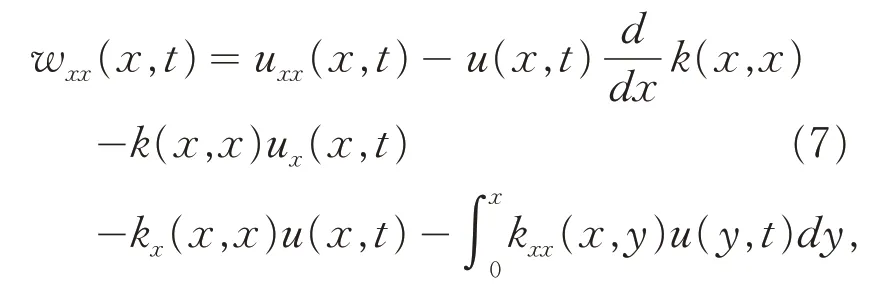
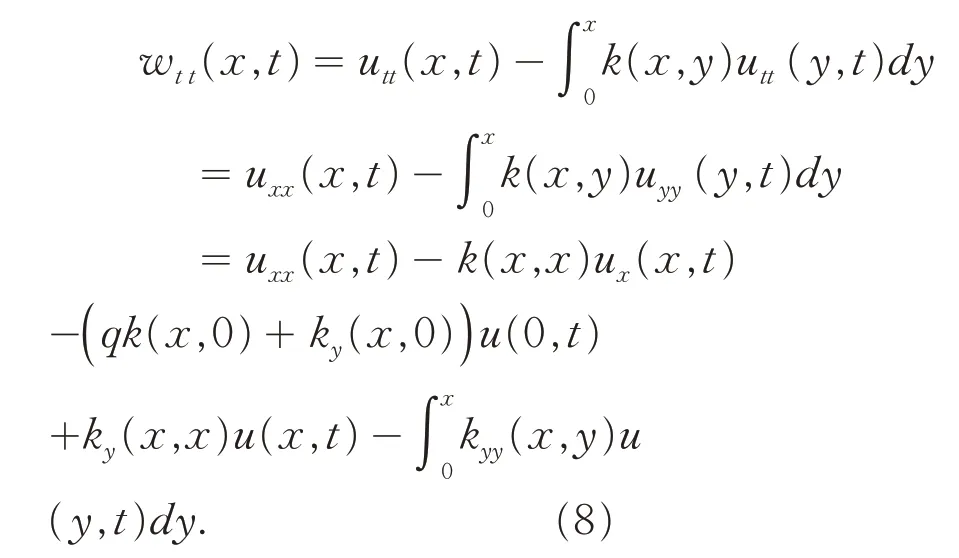
由(7)式和(8)式有:

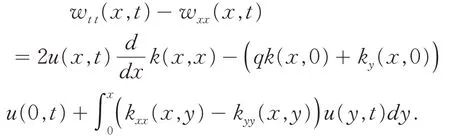
因此,为满足目标系统(2)中的方程wt t(x,t) =wxx(x,t),核函数需满足如下方程,

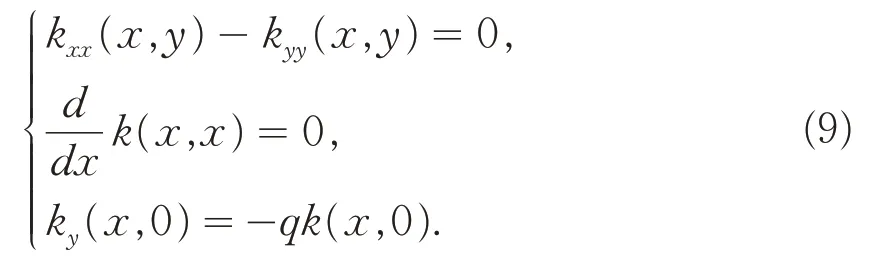
又由变换(3)和(4)以及边界条件wx(0,t) =c0w(0,t)和ux(0,t) = -qu(0,t),有:

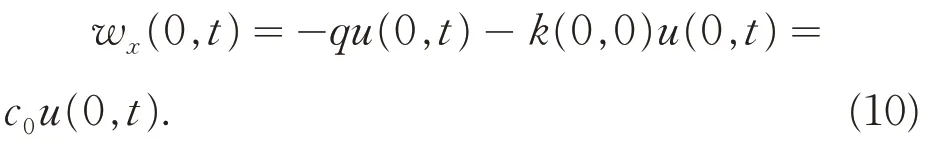
从而k(0,0) = -c0-q,又由此可得k(x,x) = -c0-q,则核函数k(x,y)满足方程,

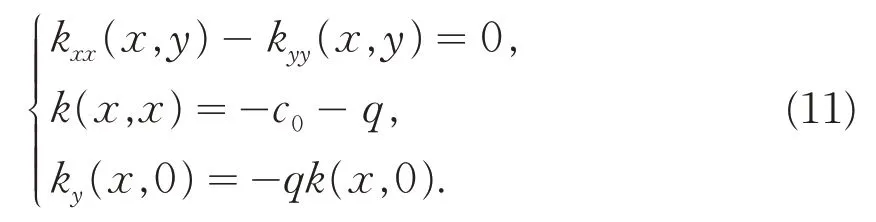
然后,求解核函数方程(11).由kxx(x,y) -kyy(x,y) = 0可得核函数可以表示成如下的形式,

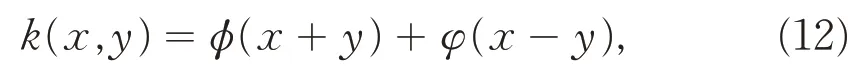
其中,φ(·),φ(·)是待确定的函数.

将(12) 式代入k(x,x) = -c0-q可得φ(2x) = -c0-q-φ(0),从而可得函数φ(x+y)为常数,由函数φ(x-y)的任意性,不妨假设:

因此,φ(0) = -c0-q. 将(12) 式代入ky(x,0) = -qk(x,0),并由(13)式和φ(0) = -c0-q可解得:

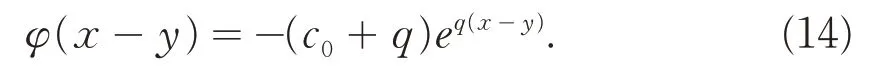
由(12-14)可得:

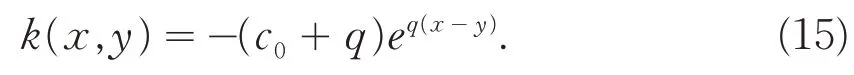
最后,将上式代入变换(3)及反馈控制器(6)中,有:

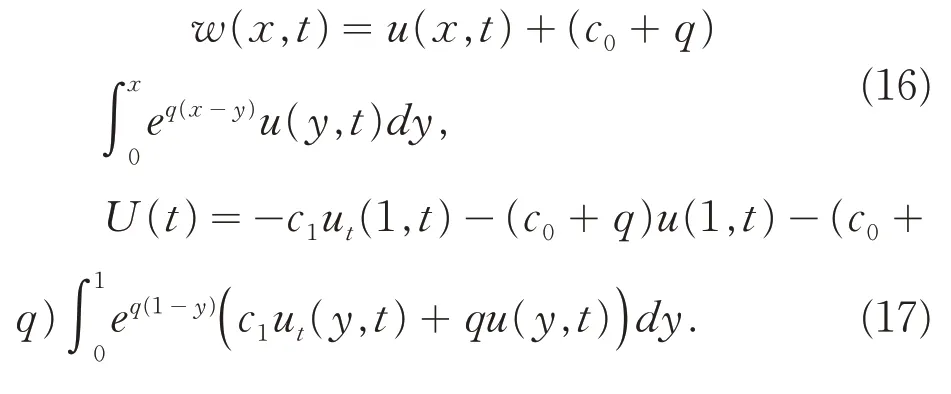
4 控制系统的稳定性

为了得到控制系统(1)的稳定性,需要寻找变换(2)的逆变换,且该变换将稳定的目标系统(2)转化为控制系统(1),参考文献[4]的证明方法,证明闭环系统的稳定性.

4.1 逆变换

首先,由文献[3]引入变换:

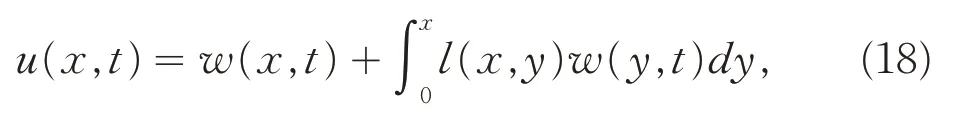
其中,l(x,y)是待定的核函数,该变换将目标系统(2)转化为控制系统(1).

运用第3节同样的方法计算ux(x,t),uxx(x,t),ut(x,t),ut t(x,t),并利用控制系统(1)和目标系统(2)中的方程以及边界条件可得核函数l(x,y)满足如下方程:

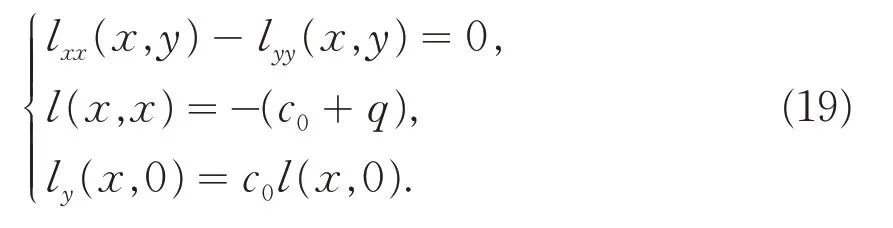
方程(19)与方程(9)类似,采用同样的方法求解方程(19)可得:

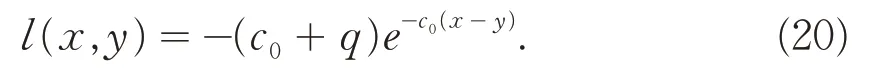
将上式代入变换(18)中,有:

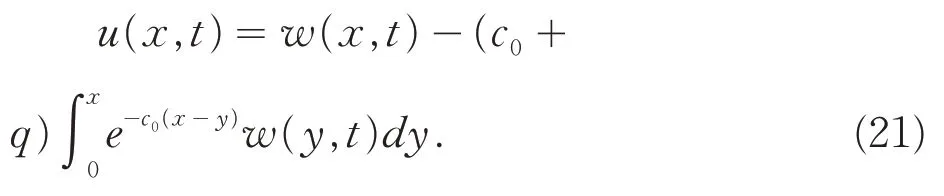
其次,需要验证变换(21)为变换(16)的逆变换.引入算子P和Q,并记:

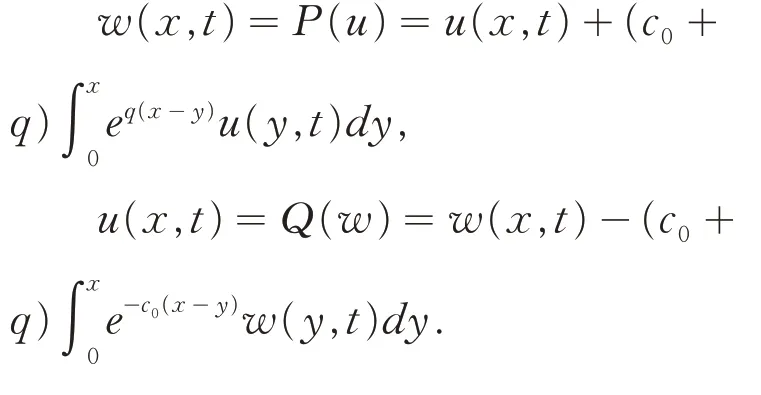
要证明变换(21)为变换(16)的逆变换,只需验证PQ=I或者QP=I,这里I为恒等变换,也即验证PQ(w) =w或者QP(u) =u,因此,将变换(21)代入变换(16)可得:

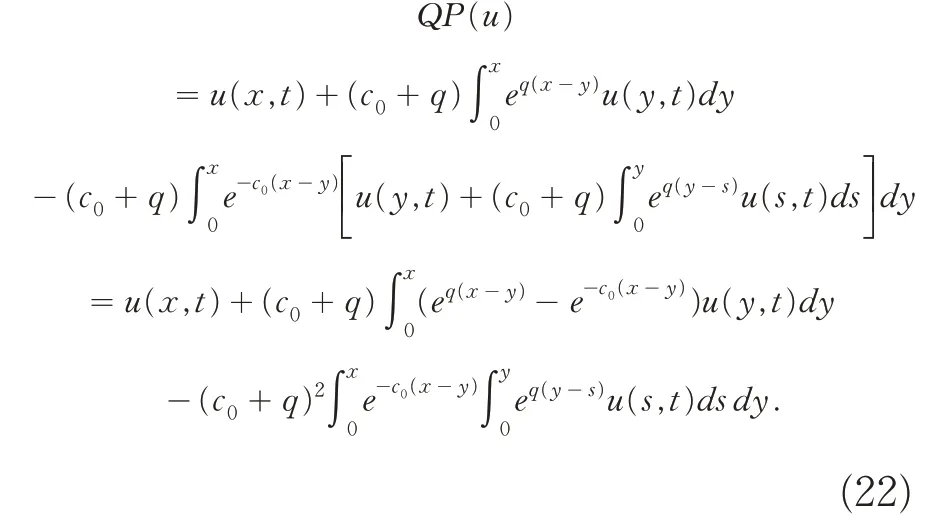
最后,交换积分顺序可得:

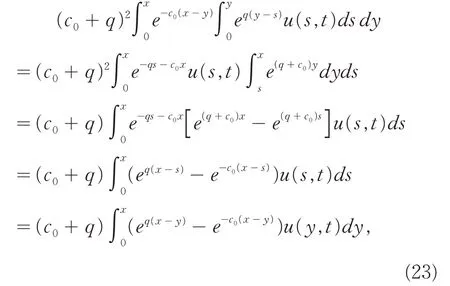
则由上式及(22) 可得QP(u) =u, 即P-1=Q,也就是说变换(16)是可逆的且它的逆变换由(21)式给出.

4.2 闭环系统的稳定性

下面将利用目标系统的稳定性和变换的有界性以及可逆性证明闭环系统在给定范数意义下的稳定性,即证明控制系统(1)在反馈控制器U(t)下是稳定的,且反馈控制器由(17)式给出.

首先,引入范数:[3][10]

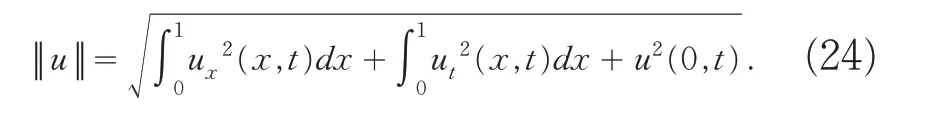
由(15)式和(20)式可得核函数k(x,y) 和l(x,y)在区域0 ≤y≤x≤1上是有界的,则算子P和Q均为有界线性算子,从而存在正数C1和C2使得下面不等式(25)成立,

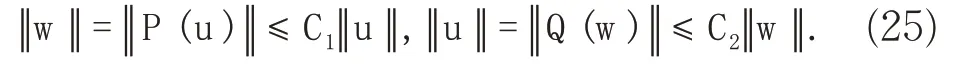
其次,记u(x,t)为控制系统(1)在初始状态u(x,0) =u0下的解,由P-1=Q可得w(x,t) =P(u)为目标系统(2)在初始状态w(x,0) =w0=P(u0)下的解,则由(25)式有,

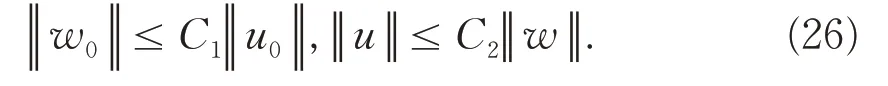
最后,由目标系统(2)的给定范数(24)下是指数稳定的,[3]可得存在正数M使得下式成立,

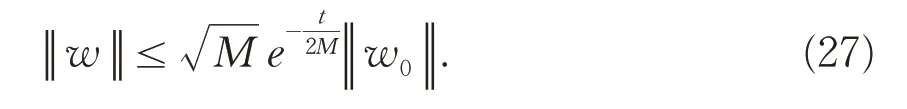
那么,由(26)式和(27)式可得,

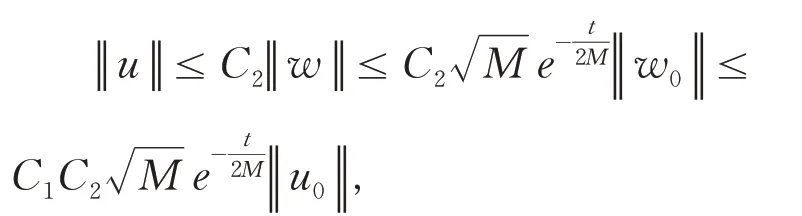
即控制系统(1)在给定范数意义下是指数稳定的.