铁路罐式集装箱堆码工况的静力学分析与试验对比

禹海燕，徐世锋，王文

（中车齐齐哈尔车辆有限公司大连研发中心，辽宁 大连 116052）

0 引言

在国内，铁路罐式集装箱适运货品类基本为中国产业升级中产生的新品类，铁路集装箱以高安全、低成本的物流方式，对国内制造业升级发展提供了有力的支撑。

罐式集装箱要取得中国船级社的定型设计批准，应提交罐箱结构强度计算书。其中，堆码工况是一个要求计算和试验的工况。它是验证满载集装箱在海洋船舶运输条件下，在箱垛中出现偏码时的承载能力[1]。

有限元方法以它的方便性和准确性特点在行业中被广泛认可。在传统计算中，只考虑采用线性方法计算，要求结构在堆码载荷下的应力不超过材料的屈服强度；而在标准试验要求中，结构可以发生永久变形，只是变形值有一定的限制，也就是结构的应力一定程度上可以超出材料的屈服强度。这样的话，传统的线性计算方法对于结构强度评价过于保守，致使依此而设计的产品质量过重而缺乏轻量化优势。若寻求到非线性有限元计算方法应用于集装箱的计算，更准确地得到结构在堆码工况下的永久变形，判断结构是否满足标准要求，可为产品轻量化提供一定的技术支持[2]。

1 分析对象和分析软件

本次计算对象为集装箱箱体结构。计算采用的软件为I-DEAS Master Series 软件和NX nastran软件，其中前者用于前处理和线性分析，后者用于非线性分析[3]。

2 载荷与工况

2.1 垂向载荷

依据ISO 1496-3-2019《系列1集装箱-规范和测试——第3部分：液体、气体及加压干散货罐式集装箱》及中国船级社的有关规定，计算主要考虑以下载荷[1]：集装箱的最大装载量P；额定总质量R；箱体自身的质量T；罐箱注满水时的装载质量W。因此，P=R-T。

2.2 堆码载荷

模拟罐式集装箱堆码的载荷，作用于罐箱顶部4个角件上。对于没有指定载荷大小的罐式集装箱，载荷大小依据罐箱类型确定。对于1D和1DX型罐式集装箱，每个角件施加堆码载荷F=224 kN；除此之外的罐式集装箱，每个角件施加堆码载荷F=942 kN。其中，每个角件的作用面积要按相同方向的偏心施加。横向偏25.4 mm，纵向偏38 mm。

2.3 堆码工况介绍

4个立柱顶部分别垂直向下作用堆码载荷。箱内载荷W，加箱体自重T，如图1所示。考虑偏载情况，若罐式集装箱两端结构对称，则仅需计算一次，否则需要更改偏载方向重新计算。

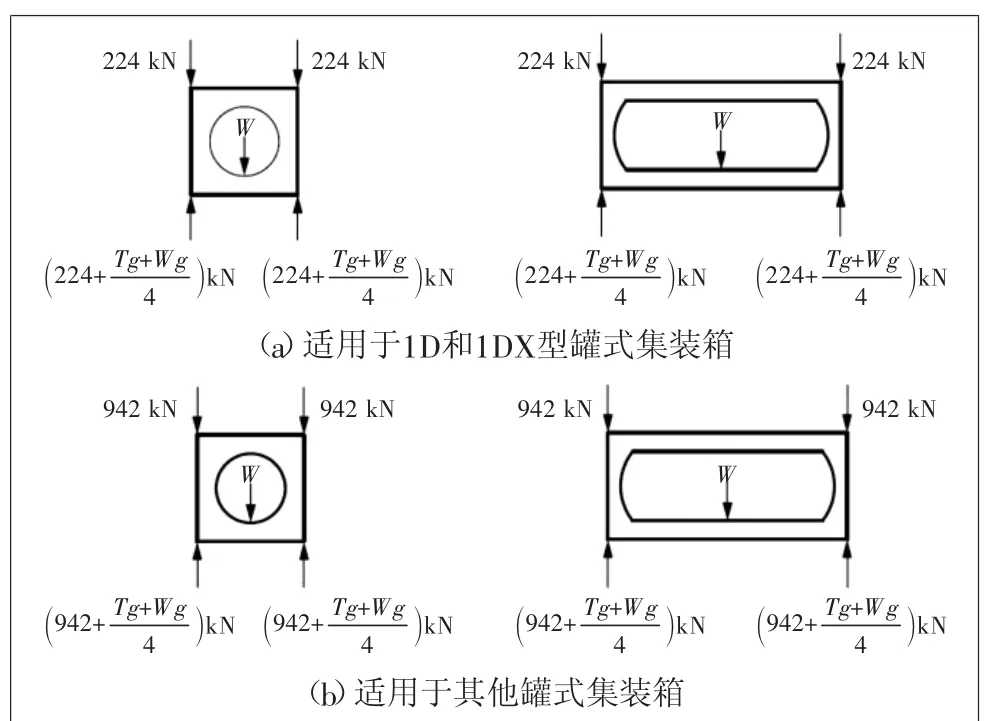
图1 堆码试验工况

3 有限元模型处理

鉴于载荷的不对称性，计算时取箱体整体结构为计算对象。若结构对称，可以建立1/2模型或者1/4模型进行对称。为了方便载荷施加，在几何结构处理时，把顶角件上平面按要求进行分割，横向每侧偏25.4 mm，纵向每侧偏38 mm。这样在网格划分后，方便载荷施加区域的选取。将角件离散为实体四面体单元，除角件外的钢结构离散为薄壳元（Thin-shell）[4]，单元长度为30 mm，并对局部结构进行细化，调整单元法向一致。模型建立好后，需要检查一下自由边，看结构是否在该连接的部位没有连接上，模型与实物的不一致会影响计算结果的准确性。箱体有限元模型如图2所示。

图2 箱体整体有限元网格及堆码载荷施加示意图

4 边界条件施加

4.1 自重施加

箱体自重载荷通过施加重力加速度的方式实现。对于步道等模型中未建立的非结构件的质量损失，在计算时通过修改重力加速度的大小进行补偿，从而使其损失的质量平均分担到整个箱体上。

4.2 载重施加

载重载荷分布于整个罐体壁面，自上而下成液体静压力分布，顶端为0，底端最大，合力为W。

4.3 堆码载荷施加

4.3.1 线性加载方式

堆码载荷按均布压力或均布节点力的方式作用于4个顶角件上，每个角件的作用面积要按相同方向的偏心施加，如图2所示。若罐式集装箱为1/4结构对称，则仅需计算1次；若为1/2结构对称，则需偏载不同方向加载计算2次；若为完全不对称结构，则需要更改偏载方向加载计算4次。

4.3.2 非线性加载方式

为使仿真更接近试验，选择高级非线性求解器，完全模拟试验过程，加载自重T、载重W和堆码载荷，然后对堆码载荷进行卸载，最后测量结构变形情况。

由于我们要计算结构的残余变形，看它是否能满足使用要求，因此就有一个载荷施加和卸载的过程，在Nastran求解器中，有两种常用的计算方案：TLA-S和ATS。其中TLA-S方法只关注结果，程序会自动分步迭代，计算出载荷施加完成的最终状态，适用于没有卸载过程，只关心最终结果的计算；而ATS方法关注过程和结果，需要载荷设置为时间相关的参数，可以有加载和卸载的过程，计算出的结果可以关注每一个时间步的状态，适合计算永久变形和残余应力，因此我们选择ATS方法。

如果要算卸载过程的话，载荷值需要随时间变化，此时力的大小不是恒定值，而是时间的函数。这里的时间设置要与载荷步设置相对应。例如前面载荷步一共设置了10步，每步1 s，一共10 s，所以这里也要输入10 s的数据。数据点最少3行，分别是：第一行初始点，0 s，载荷为0，输入0；中间行，某个时间，达到最大值，载荷输入最大值；最后一行，最后时刻，卸载完，载荷输入0。

在非线性分析中，需要使用材料的应力应变曲线，若没有具体数据，可采用简化的双线性曲线来模拟材料的本构关系。

4.4 约束施加

在堆码工况中，对罐式集装箱4个底角件进行全约束，即UX=UY=UZ=0，其中：X向为箱体纵向；Y向为箱体横向；Z向为箱体垂向。

5 数据对比

为了验证计算方法的合理性，对某型罐式集装箱进行了仿真计算和试验，并进行了计算结果与试验数据的对比。

该箱体总容积为29.5 m3，自重为4700 kg，载重为25 780 kg。角柱、纵向梁、端框斜支撑和裙圈材料为Q450NQR1，屈服强度为450 MPa，筒体、封头、上侧梁、下侧梁、端梁等结构材料为Q345D，屈服强度为345 MPa。

5.1 试验布点图

根据仿真计算的应力结果，选取计算中的应力大的点作为重点关注部位。堆码工况下，应力大的点主要分布在角柱上。试验布点图如图3所示。

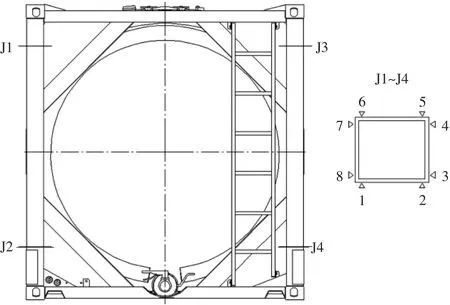
图3 布点图

5.2 线性计算对比

此罐式集装箱为1/4对称结构，堆码工况偏载计算一次即可。通过线性计算，得到罐式集装箱箱在堆码工况下的应力云图，如图4所示。从图4中看到，框架结构上最大应力为432 MPa，小于材料的屈服强度450 MPa。

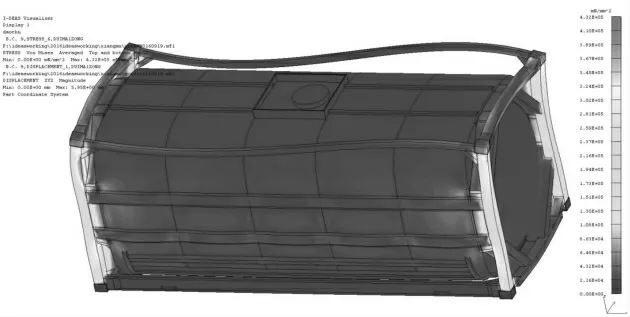
图4 堆码工况应力云图

选择实测应力较大的部位进行对比，共进行了2个罐的试验，每个罐进行了3次试验，分别对3次试验取平均值作为试验对比值并做了柱状对比图（如图5）。

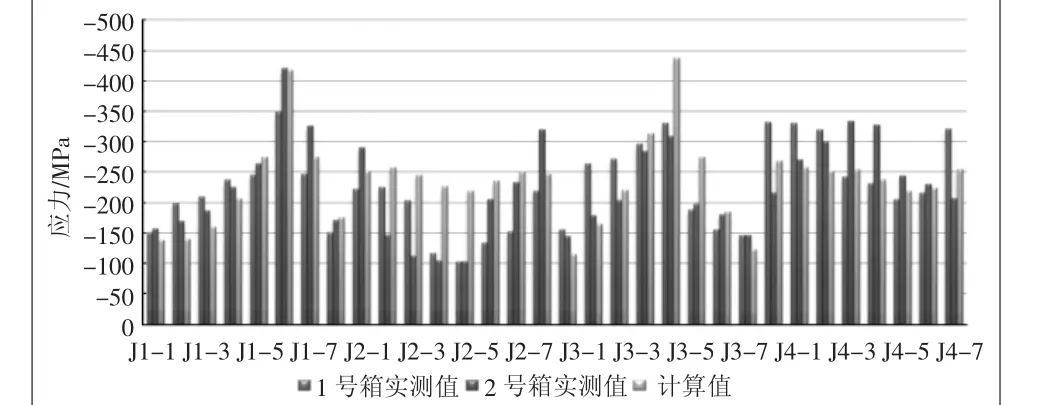
图5 堆码工况应力计算与试验数据对比柱状图

从对比中得到，堆码工况计算应力值与实测应力值大部分比较接近，个别点误差较大，原因可能为贴片点和取值点位置不精确，计算模型较为理想和实际模型有差别等。总体来看趋势一致，基本符合工程上的精度要求。

5.3 非线性计算对比

经过非线性计算，卸载后的位移云图如图6所示。根据ISO/TR 15070-1996《系列1集装箱——箱体结构试验值的理论基础》要求，堆码载荷卸载后角柱上水平方向最大残余变形应不超过2 mm，下侧梁和横梁最大位移应不超3 mm[5]。

从图6中看出，角柱上水平方向最大残余变形为0.02 mm，小于2 mm；下侧梁和横梁最大位移为0.97 mm，小于3 mm，满足试验要求。计算与试验残余变形值对比如表1所示。

图6 卸载后位移云图

从表1中看出，变形值测量上的精度没有计算高，取值基本为0、0.5和1.0，因此实测误差比较大。计算值与实测值趋势一致，数值也较接近，因此计算满足工程精度要求。

表1 堆码工况残余变形计算与实测对比表

6 结语

本文针对普通罐式集装箱的堆码工况，以某箱为例，进行了线性有限元分析和非线性有限元分析，分别与试验结果进行了数据对比。分析结果表明，本文采用的分析方法基本满足工程上的精度要求。因此，在堆码工况计算时，若线性计算结果不超出材料的屈服强度，则不需要进行非线性计算，否则可以按照本文方法进行非线性计算，计算得到的残余变形满足设计要求即可。