基于单目视觉三维恢复算法的微观形貌原位测量方法研究

安奕同，周平，闫英

（大连理工大学 精密与特种加工教育部重点实验室，辽宁大连 116024）

0 引言

工件表面的微观形貌分析一直是机械加工及测量领域研究的热点，对优化工艺方法、提高工件表面质量发挥着重要作用[1]。现有的先进测量手段可以获取工件表面的三维形貌，实现更加直观的测量结果。例如激光共聚焦显微镜能够利用激光扫描获取工件表面三维形貌，并对表面进行参数分析[2]。但是这些技术设备不仅造价昂贵，还需要将零件拆卸或分解并在实验室环境中测量，难以应用于现场检测和原位测量，始终无法突破对表面微观形貌原位测量的壁垒[3]。

随着计算视觉技术的发展，计算机视觉技术在工件表面检测上的应用也越来越受到关注。计算机视觉技术克服了传统方法的不足，具有简单快捷、无接触、无变形等优点。基于单目视觉的SFS（shape from shading，从明暗恢复形状）方法和光度立体视觉技术是计算机视觉技术在三维形貌恢复的手段，可以获取工件表面法向量，还可以高精度恢复表面形貌，因而成为机器视觉领域研究热门。

本研究的目的是将SFS方法和光度立体法应用于工件表面微观形貌的三维恢复，分析其算法性能，提出一种通过二维图像进行三维形貌恢复的原位测量方法，为超精密加工在线测量提供新方法。

1 三维重构算法

1.1 Shape from shading

1970年，Horn[4]提出从明暗恢复形状算法（Shape from shading），最初目的是用于月球表面重建。该方法利用物体表面二维图像的灰度变化来恢复其表面各点的高度信息，从而实现对零件图像表面微观形貌的三维重建。

SFS方法可以划分成4种类别，包括最小化方法、传播方法、局部方法和线性方法[5]。为了满足算法简单易实现、快速、易收敛的要求，本文采用Tsai-Shah线性方法，详细介绍具体步骤。

首先将表面梯度进行离散估计。朗伯体表面的反射图函数如下：

假设初始高度为0，经过10次迭代后表面高度即可收敛平滑，整体算法流程如图1所示。

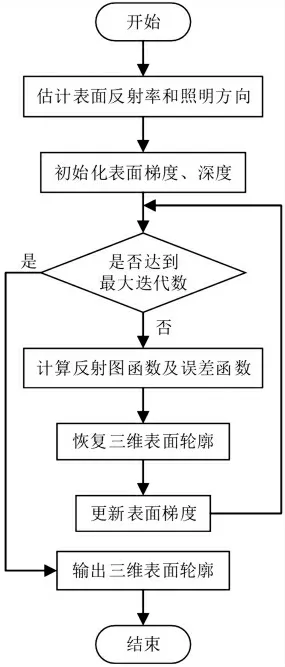
图1 本文SFS算法流程图

1.2 光度立体技术

1980年，Woodham[6]提出了光度立体法，在保持相机视野不变的情况下，利用不同方向光源，对光源添加约束，令上述问题存在唯一解。光度立体法原理可以描述为：在不同但可控的光照条件下，得到物体表面上同一视点的图像。基于这些图像和物体表面的反射模型，计算物体表面的法向量，然后恢复物体表面的三维形貌。

在恢复过程中，采用了朗伯体反射模型[7]。假设存在n个光源，它们的位置形成一个光源方向矩阵L=[L1，L2…Ln]T（理论上只需要3个方向的光源，但实际上会使用更多数量的光源消除误差），其中Ln表示第n个光源方向矢量。在n个光源的依次单独照明下，表面上同一点会得到n个表面亮度I=[I1，I2…In]，其中In表示在第n个光源照明下所得到的表面亮度。如果表面上一点的法 向 量 为N=[n1，n2，n3]T，则朗伯体模型可表示为

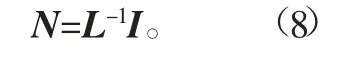
使用近点光源校准方法获得入射光的信息，包括入射光的强度和方向。同时，根据图像中每个像素点的灰度值，得到每个点的反射亮度，并根据式（8）计算出表面点的法向量，主要步骤如下：

第一步。如图4所示，使用具有12个圆形均匀分布光源的电子显微镜来获得工件表面的二维图像。图2显示了在12个光源的不同方向照明下的SiC工件表面图像。

图2 12个不同方向光源依次照射下获得的图像

第二步。计算物体表面的法向量。使用图2中的图像，工件表面上一点的法向量可以通过式（8）计算。以此类推，将上述算法应用于图像的所有像素即可得到工件表面图像所有点的法向量。

第三步。通过对向量域进行积分获得表面深度信息。将得到的法向量归一化，得到工件表面梯度域，最后通过对法向量积分来恢复表面的深度信息。表面深度的计算方法与Agrawal 所提出的方法[8]相同，本文光度立体法流程如图3所示。

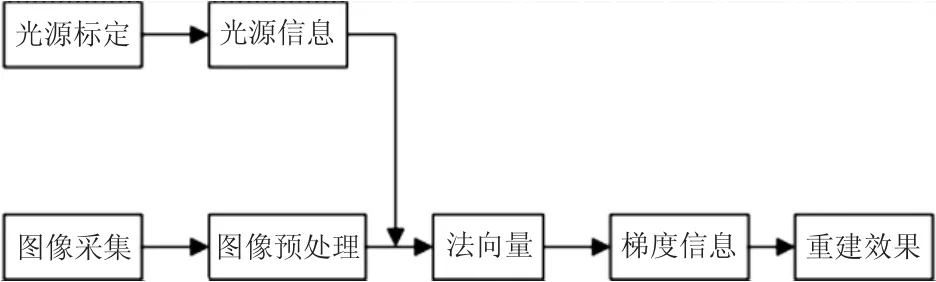
图3 本文光度立体法流程图

2 试验与分析

基于上文提及的微观形貌原位测量方法，设计了二维图像采集系统，并将其用于工件表面的检测，最后比较恢复结果与共聚焦显微镜扫描结果，验证所提方法的准确性。

2.1 图像采集系统

本文设计了微观三维形貌的原位测量系统，该系统包括FT-UMS1000电子显微镜头、一个 同 轴 光 源、12 个环形均匀分布的光源，如图4所示。

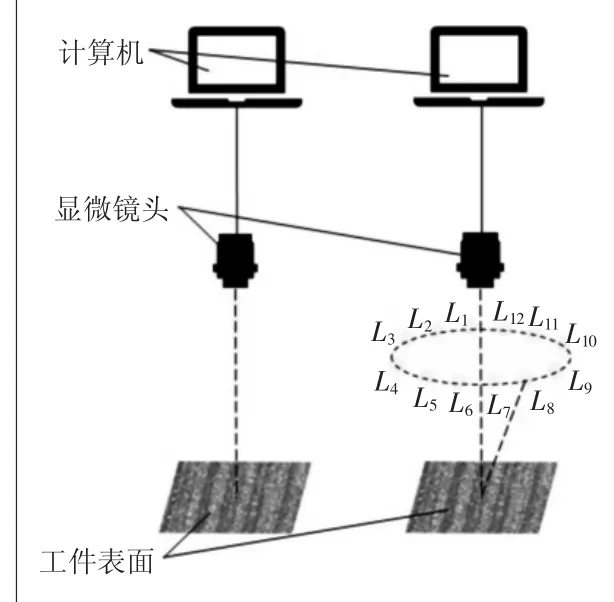
图4 SFS方法（左）及光度立体法（右）试验方案

系统工作原理为将显微镜头对准所测工件表面并对焦，通过同轴光源照明获取SFS 算法所需平面图像；然后关闭同轴光源，依次切换12个光源照明获得12幅单光源照明下的平面图像，接下来利用上文提及的恢复算法实现工件表面微观三维形貌的获取。

2.2 验证试验方案

本文的试验对象SiC为工件表面，利用SFS算法以及光度立体法对其微观表面进行三维形貌恢复与特征参数计算，同时利用激光共聚焦显微镜（Laser scanning confocal microscopy，LSCM）对同位置进行扫描，以验证两种三维形貌恢复方法的准确性。

为了验证两种恢复方法对表面三维形貌恢复结果的准确性，本文随机选择并标记了两处特征位置进行重构试验，同时也保证了两种方法与LSCM测量的可比性，试验工件及测量位置如图5所示。

图5 SiC工件试验对象及测量位置

使用两种方法与LSCM分别得到三维形貌后，分别比较高度图、特征位置截线及特征点、截线二维参数和三维参数，以验证两种方法对表面形貌恢复的准确性。

2.3 试验结果与分析

将SiC工件分别置于一般环境下电子显微镜头与试验室环境下的LSCM下，得到了两个测量位置的二维图像，如图6和图7所示。

图6 不同手段获得SiC工件表面测量位置1二维微观形貌

图7 不同手段获得SiC工件表面测量位置2二维微观形貌

2.3.1 SiC工件表面位置1测量

通过SFS方法和光度立体法分别对采集的二维图像进行三维重构恢复，并利用LSCM对相同区域进行激光扫描，获得三维形貌如图8所示，高度图如图9所示。

图8 不同手段获得测量位置1三维微观形貌

通过观察图9高度图，SFS方法得到的三维形貌高度分布一致性较差，光度立体法与LSCM的高度分布基本一致。分别选取高度图中标记截线处，绘制轮廓曲线，如图10所示。

图9 不同手段获得测量位置1高度图

通过观察截线对比图可知，SFS方法走势相差较大，故不再详细进行参数对比；而光度立体法与LSCM截线走势基本一致，峰谷基本对应；故接下来选择图10中光度立体法及LSCM截线上所示两组对应特征点，定量对比每组特征点之间的高度差、宽度差及绝对误差，如表1所示。

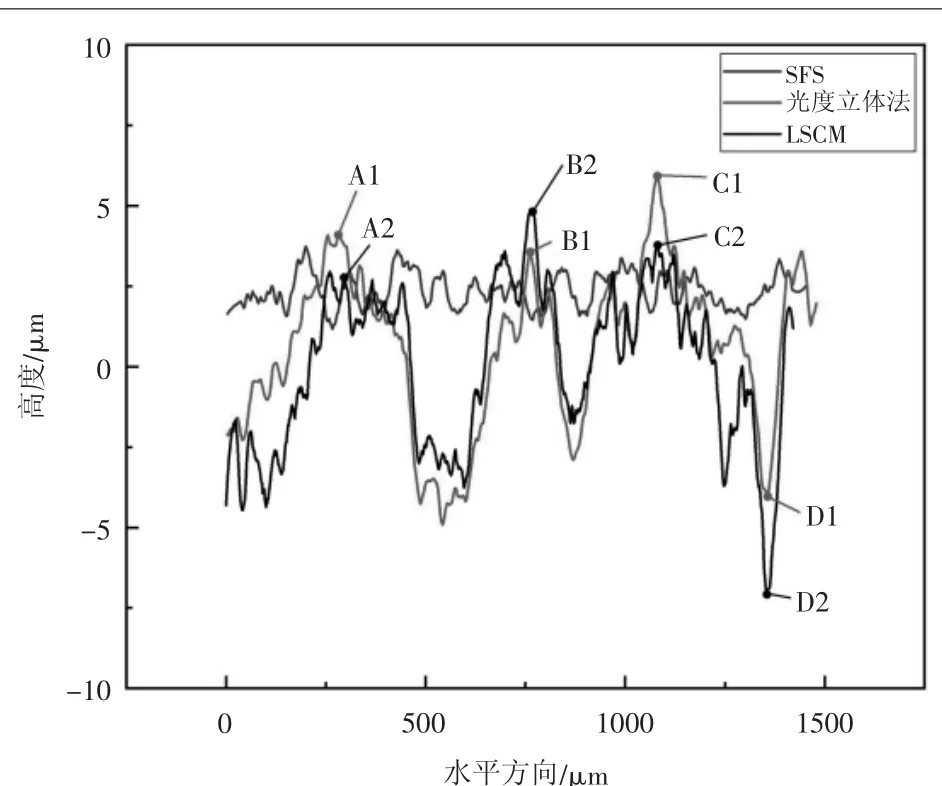
图10 不同手段获得测量位置1截线对比图

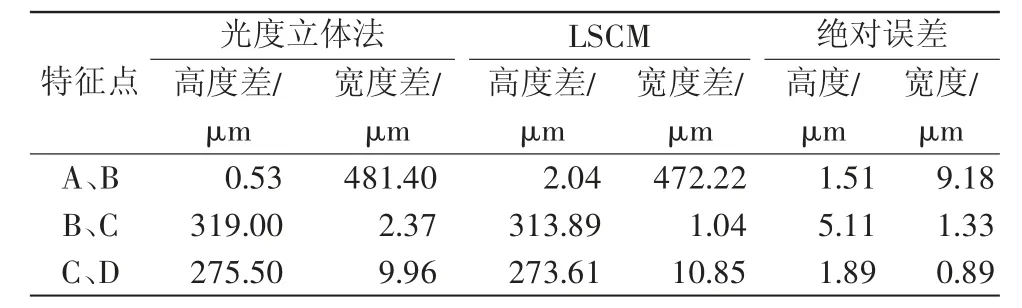
表1 测量位置1截线特征点对比

由表1可知，与LSCM相比，宽度差误差最大值为9.18 μm，其相对误差为1.94%，高度差误差最大值为5.11 μm，其相对误差为1.63%。

然后使用两种手段分别获取截线二维参数并比较，包括算数平均高度Ra、均方根高度Rq、最大峰高度Rp、最大谷深度Rv、最大高度Rz，反映截线高度分布的偏度Rsk、峰度Rku，结果如表2所示。

表2 测量位置1截线二维参数对比

由表2可知，相对于LSCM图像，光度立体法算术平均高度误差值为0.310 μm，其相对误差为13.6%；均方根高度误差值为0.291 μm，其相对误差为10.7%;最大高度误差值为5.282 μm，其相对误差为32.8%。Rsk都低于0，表明轮廓有较少的凸台和尖峰；Rku都低于3，截线高度分布均匀。

使用两方法对图9测量位置1的三维参数进行获取和比较，包括算数平均高度Sa、均方根高度Sq、最大峰高Sp、最大谷深Sv、最大高度Sz、反映表面高度分布的偏斜度Ssk、峭度Sku，结果如表3所示。

表3 测量位置1重构图像三维参数对比

通过观察表3可知，光度立体法所得表面三维算术平均高度误差为0.277 μm，其相对误差为13.2%；三维均方根高度误差为0.488 μm，其相对误差为19.6%；最大高度误差值为5.282 μm，其相对误差为8.03%。Ssk值都低于0，表示高度分布相对于平均面偏上，与特征位置三维形貌相符；Sku值都低于3，表示形貌高度分布均匀，与特征位置三维形貌相符。

综上分析，对于SiC工件表面位置1，与LSCM相比，SFS方法重构结果较差；光度立体法三维模型直观形貌、高度分布、取样截线走势均一致较好；各二维参数中，最大高度相对误差最大，为32.8%，峰度及偏度判断结果一致。各三维参数中，均方根高度相对误差最大，为19.6%，偏斜度及峭度判断结果一致。

2.3.2 SiC工件表面位置2测量

同样利用SFS方法、光度立体法LSCM分别对测量位置2采集二维图像；随后进行三维重构恢复，获得三维表面形貌，如图11所示。各方法高度图如图12所示，通过观察可以看出，SFS方法结果依旧不理想，高度分布不一致；光度立体法重构结果较理想，表面纹理、高度分布基本一致，各方法相似位置截线对比如图13所示。

图11 不同手段获得测量位置2三维微观形貌

图12 不同手段获得测量位置2高度图

由图13可以观察到，SFS方法所得截线符合度较差，故考虑不再参与后续参数对比；光度立体法与LSCM所得截线走势一致，符合度较好。接着选取光度立体法和LSCM截线上两组对应特征点，并比较每组特征点之间的高度差、宽度差及其绝对误差，结果如表4所示。

图13 不同手段获得测量位置2截线对比图

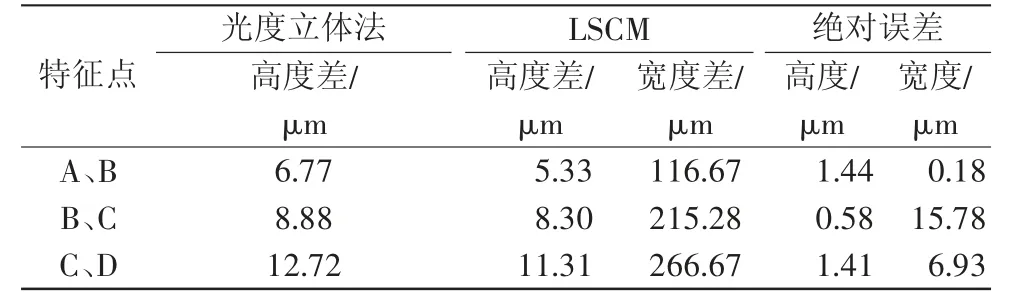
表4 测量位置2截线特征点对比

由表4可知，与LSCM相比，宽度差误差最大值为15.78 μm，其相对误差为7.33%，高度差误差最大值为1.44 μm，其相对误差为27.02%。

接着提取并对比截线的二维参数，包括算数平均高度Ra、均方根高度Rq、最大峰高度Rp、最大谷深度Rv、最大高度Rz，表示截线高度分布的偏度Rsk、峰度Rku，结果如表5所示。

表5 测量位置2截线二维参数对比

由表5可知，相对于LSCM图像，光度立体法算术平均高度误差值为0.336 μm，其相对误差为14.7%；均方根高度误差值为0.731 μm，其相对误差为25.3%;最大高度误差值为1.675 μm，其相对误差为13.4%。Rsk都低于0，表明轮廓有较少的凸台和尖峰；Rku都低于3，表明截线高度分布均匀，二维参数结果与直观观察相符。

最后对两种手段测量位置1的三维参数进行提取与对比，包括算数平均高度Sa、均方根高度Sq、最大峰高Sp、最大谷深Sv、最大高度Sz、反映表面高度分布的偏斜度Ssk、峭度Sku，结果如表6所示。

通过观察表6可知，光度立体法所得表面三维算术平均高度误差为0.471 μm，其相对误差为19.4%；三维均方根高度误差为0.220 μm，其相对误差为13.5%；最大高度误差值为1.641 μm，其相对误差为8.5%。Ssk值都低于0，表示高度分布相对于平均面偏上，与特征位置三维形貌相符；Sku值都低于3，表示形貌高度分布均匀，与特征位置三维形貌相符。

表6 测量位置2重构图像三维参数对比

综上分析，对于SiC工件表面位置2，与LSCM 相比，SFS方法重构结果较差；光度立体法三维模型直观形貌、高度分布、取样截线走势均一致较好；各二维参数中，均方根高度相对误差最大，为25.3%，峰度及偏度判断结果一致。各三维参数中，算术平均高度相对误差最大，为19.4%，偏斜度及峭度判断结果一致。

3 结语

本文将基于单目视觉的SFS方法和光度立体法应用至微观形貌的原位测量领域，提出了一种通过单目显微镜头采集二维平面图像恢复三维表面形貌的方法。该方法将SFS方法和光度立体法所得重构结果与激光共聚焦显微镜扫描结果比较，包括二维轮廓线、二维表面形貌参数、三维表面形貌参数，结果表明：SFS方法仅靠一张图像作为输入，深度信息丢失较多，同时在一般光照环境下，受阴影、噪声等影响，对SiC工件复杂表面重构结果不理想；光度立体法利用多角度光源拍摄，得到更多表面信息，求解得到更精确的表面法向量，可以获得较为精确的重构表面。

本文提出的方法能够应用于机械工件表面微观形貌的三维重构与参数分析，相比于传统的工件加工后拆卸并测量的方式，无需拆卸工件，可对工件加工状况提供及时的反馈，更加节约时间；同时测量设备经济、体积小，为解决机械零件表面微观形貌原位检测与三维分析难题提供了一种新思路。