基于扩张观测器的PMLSM非奇异快速终端滑模控制*

2022-12-21索宇超杨永宝牟明川

组合机床与自动化加工技术 2022年12期

索宇超，张博，周达，杨永宝，牟明川

(1.西安工程大学电子信息学院，西安 710600；2.南京国电南自维美德自动有限公司，南京 210000)

0 引言

永磁直线同步电机(permanent magnet linear synchronous motor，PMLSM)直接将电能转换成直线运动，其具备结构简单、响应速度快等优势，因此被广泛应用在自动化生产线，超精密加工机床，民航运输等领域[1-3]。然而，由于采用PMLSM直接驱动系统，缺少减速器和转换装置，使其控制系统的柔性变差，即对控制系统参数变化和负载扰动较敏感[4-5]。

滑模控制(sliding mode control，SMC)有响应速度快、对参数变化及扰动不灵敏等优点，尤其在电机控制领域有着广泛的应用。传统的SMC通过控制增益来确保鲁棒性，但较大的控制增益会带来抖振现象[6-7]。为了减少抖振，国内外学者提出了不同的控制方法。柯希彪等[8]设计积分滑模面来削弱抖振，系统的响应速度得到提高，但当负载扰动过大时，系统的精度会变差。丘永亮等[9]通过分数阶滑模的特性来降低系统的抖振，提高系统的动态性能，但分数阶仅存于理论研究。ZHAO等[10]提出了改进终端滑模控制方法，可以消除传统终端滑模算法奇异性问题，并能保证在有限时间内沿所设计的滑模面收敛到零，从而提高了系统的跟踪精度，然而，当系统受到扰动后，控制系统的动态响应并未得到改善。

采用非奇异快速终端滑模控制算法设计系统的控制器，不仅可有效削弱系统的抖振，还可以保证在有限时间内位置误差变量收敛到零。同时，提出采用扩张观测算法[11-13]控制系统的负载扰动，从而实现系统前馈补偿控制，以提高控制系统的动态性能。最后通过仿真，证明了本文提出方法的有效性。

1 PMLSM系统数学模型

PMLSM驱动系统是一种非线性、强耦合系统，为了简化，采用id=0的磁场定向控制，对三相PMLSM驱动系统，其电磁推力方程为[14]：

(1)

式中，Fe为电磁推力；kf为推力系数；iq为q轴的电流；τ为永磁体极距；np为电机的极对数；ψf为永磁体磁链。

PMLSM动力学方程为：

(2)

式中，M为电机的质量；B为粘性摩擦系数；v为动子的运动速度；Fd为系统的摩擦力、负载扰动和参数变化等不确定性的总和。

忽略系统摩擦，PMLSM系统的运动方程为：

(3)

(4)

式中，u为控制器的控制律：u=iq；y为系统的输出变量，为位置信号。同时，设xd为给定的位置参考信号，并给出如下的假设。

假设1：xd具有2阶连续可微且有界；

2 控制器设计

基于非奇异快速终端滑模和ESO相结合的复合控制PMLSM伺服系统框图如图1所示。设计位置控制器让PMLSM伺服系统在受负载扰动、参数变化等不确定时，电机实际位置信号x1号能够跟踪任意给定输出的位置信号xd。

图1 基于扩张观测器的非奇异快速终端滑模控制PMLSM伺服系统框图

定义位置和速度误差为：

e=x1-xd

(5)

(6)

2.1 滑模控制器设计

定义滑模面：

(7)

式中，∂1与∂2大于0；k1∈(1,2)；k2>k1。

当系统状态到达滑模面(s=0)时，式(7)满足：

(8)

由式(8)中可以得出：

(9)

假设系统的收敛时间是t。对式(9)两边微分：

(10)

(11)

(12)

从式(12)可以得出当确定了滑模面及其参数，系统的跟踪误差将在有限时间内沿滑模面收敛为零。

对式(7)求导得：

(13)

将式(6)和式(4)带入式(13)得：

(14)

控制律u：

(15)

式中，

2.2 时变控制增益设计

在电机实际运行中，系统不确定性ki是很难准确获得。本文以分段逻辑函数的形式来给出非奇异终端滑模控制增益ki。

逻辑函数(或逻辑曲线)对具有极限的指数增长建模的函数。它是一种常见的“S”形(S型曲线)，其方程为[15]：

(16)

式中，a表示较低的渐近线；L表示曲线的最大值；p表示对数增长率；tm表示S型曲线的中点。

(17)

2.3 系统稳定性分析

构建Lyapunov函数为：

(18)

对式(18)求导，并将式(13)和式(15)带入：

kisign(s))≤|s||ds|-ki|s|≤-|s|(ki-|ds|)≤0

(19)

3 复合控制系统设计

3.1 扩张状态观测器设计

为了提高系统的抗干扰能力，本文设计了ESO来观测负载扰动。将观测到的负载扰动用于滑模控制器当中。

假设：x3=ds。重写系统的状态方程：

(20)

式中，m(t)为负载ds的变化率。

系统的ESO设计如下：

(21)

式中，z1、z2、z3分别是x1、x2、x3观测值；λ是控制器的系数。

3.2 NFTSMC+ESO复合控制器设计

将3.1节设计的ESO应用于滑模控制器中，得复合控制器的输出控制量为：

(22)

式中，z3为ESO观测的负载扰动值。

4 仿真与结果分析

基于以上理论，设计出了基于ESO的非奇异快速终端滑模控制器，设计的控制器系统总框图如图1所示。

为了验证本文所提的控制策略的有效性，对PMLSM驱动位置控制系统设计仿真对比实验，PMLSM的参数如表1所示。

表1 电机参数

控制器参数为：

∂1=30；∂2=20；k1=1.5；k2=1.8；L1=5；
L2=17；p=1000；tm=0.13；ki(0)=18；λ=600。

(1)输入位置信号为阶跃信号。①位置给定信号为1.2 mm，保持其他参数不变的情况下，在t=3 s时突加60 N的负载扰动。本文提出的控制算法和非奇异终端滑模控制算法位置跟踪曲线如图2所示。本文提出的控制算法在电机启动过程中能平稳运行，最终在0.3 s跟踪到给定位置信号。而基于非奇异终端滑模控制算法在0.5 s后跟踪到给定位置信号，通过仿真实验对比分析，本文提出的控制算法动态响应快。②基于非奇异终端滑模控制算法和本文所提出的控制算法所设计的位置控制器，其位置误差曲线如图3和图4所示。从图3可知，当系统在3 s突加60 N外部扰动后，基于非奇异终端滑模的位置误差迅速增大到3.9 μm，在3.3 s时能跟踪到给定位置信号，平稳运行。图4可知，当系统在3 s突加60 N外部扰动后，本文提出的算法位置误差增大到3 μm，在3.09 s能跟踪到给定位置信号，平稳运行。通过图3和图4对比分析，可知本文提出的控制算法，在突加外部扰动时位置误差小、跟踪位置信号响应速度快，能快速达到稳定。

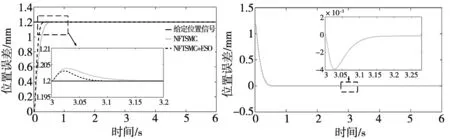
图2 控制系统位置跟踪曲线图3 NFTSMC位置误差曲线

图4 NFTSMC+ESO位置误差曲线

(2)输入位置信号为正弦波信号。为了验证控制器的跟踪性能，给定一个幅值为1.2 mm周期为2 s正弦波参考轨迹作为给定的位置输入信号，如图5所示。在3 s时突加60 N负载扰动，基于非奇异终端滑模控制算法和本文提出的控制算法误差曲线分别如图6和图7所示。从图6可知，当系统在3 s突加60 N负载扰动时，基于非奇异终端滑模的位置误差突然增加到3.8 μm在3.15 s左右达到稳定，但是稳定在0.5 μm附近；从图7可知，本文提出的算法位置误差突然增加到2.6 μm在3.08 s左右达到稳定并且在0附近。因此，本文所提出的控制方法非奇异终端滑模控制方法，其位置跟踪精度高，鲁棒性能强。