增强MCKD和增强EWT的轴承滚珠微弱故障检测*
2022-12-21陈小怡魏圣坤
陈小怡,魏圣坤
(泸州职业技术学院智能制造与汽车工程学院,泸州 646000)
0 引言
滚动轴承是机床设备的核心部件之一,轴承正常运行对于整机而言有重要意义[1]。滚动轴承的故障主要包括内圈故障、外圈故障、保持架故障和滚珠故障[2]。轴承滚珠处于轴承内部,振动信号传递路径复杂,发生故障时故障信息较为微弱[3]。目前,轴承滚珠故障检测方法主要基于数据驱动或物理模型。建立物理模型需要对设备深入了解,然而设备中与轴承关联的部件众多,因此难以建立轴承物理模型。因此本文采用主流的基于振动信号的数据驱动方法对轴承滚珠进行故障检测。
为了从采集到的振动信号中提取轴承滚珠故障特征,离散小波变换(discrete wavelet transform,WT)、经验模态分解(empirical mode decomposition,EMD)、集合经验模态分解(ensemble empirical mode decomposition,EEMD)、局部均值分解(local mean decomposition,LMD)等现代信号处理方法被提出,这些方法可以从振动信号中提取故障特征,但同时也存在着一些问题。DWT对信号的频谱进行二进分割,缺乏自适应性[4];EMD和LMD存在模态混叠和端点效应的问题[5];EEMD缓解了模态混叠问题,但添加的噪声参数难以确定,且计算量较大[6]。经验小波变换[7](empirical wavelet transform,EWT)结合了DWT和EMD的优势,通过对轴承振动信号的频谱进行自适应分割进而将复杂信号分离成一系列调幅调频分量(amplitude modulation-frequency modulation components,AM-FM)。EWT较好地缓解了模态混叠和端点效应等问题,在轴承故障检测领域得到了一定应用。李志农等[8]利用EWT对轴承振动信号进行分解,但是环境噪声使EWT分解得到的AM-FM分量过多,影响后续故障检测,且针对轴承滚珠微弱故障检测效果较差;唐泽娴等[9]研究了利用频谱聚类改进EWT的分解性能,但频谱聚类方法极易受噪声影响,分解效率低,对轴承滚珠故障检测效果差。在环境噪声条件下,EWT存在严重的过分解问题[10]。
最大相关峭度解卷积[11](maximum correlated kurtosis deconvolution,MCKD)以相关峭度最大为目标突出信号中被噪声淹没的周期性故障信息,对微弱故障成分有较好地提取效果。唐贵基等[12]研究了直接利用MCKD提取轴承滚珠微弱故障信息,但MCKD受滤波器阶数和冲击信号周期影响较大。
对在噪声环境下采集到的轴承滚珠故障振动信号,本文采用对噪声鲁棒性的功率谱熵(power spectrum entropy,PSE)作为评价信号故障成分所占比重的指标,采用PSE对MCKD参数进行自适应选取,免去了繁琐的人工选取参数的过程;然后提出一种新的EWT频谱有效边界划分方法,有效地缓解了EWT的过分解问题,并将振动信号自动分解为若干AM-FM分量;最后提出一种新的AM-FM分量筛选指标,综合考虑了峭度和相关系数两个指标,能更有效地选取主要的模态分量,试验验证了提出方法的有效性。
1 EMCKD降噪
滤波器阶数L和解卷积周期T是MCKD的两个重要参数,参数的选择决定了MCKD的性能。理论上T的表达式为:
(1)
式中,fs为采样频率;f0为故障特征频率。
实际工程中T的取值会与理论值略有差别,因此需要在理论值附近对T进行寻优。L的选择范围一般为0~500。由于L和T相互影响,因此研究两个参数的自适应选取对MCKD算法效果的提升有重要意义。轴承滚珠振动信号功率的不确定性越小,则功率谱熵越小,若功率在各个频率上分布均匀,则不确定性较大,功率谱熵也随之增大。因此可将功率谱熵作为评价信号故障成分所占比重的指标,功率谱熵越小,故障频率在功率谱上越明显,越能提高故障检测准确率。因此本文提出基于功率谱熵评价准则的参数自适应选取方法,以功率谱熵最小作为参数自适应选取的评价准则,参数寻优法采用网格搜索算法[13]。基于功率谱熵评价准则的MCKD参数自适应选取方法表述如下。
设信号采样频率为fs,采样点数为N,y(n)的功率谱密度计算如下:
(2)
式中,y(n)为振动信号;Y(wi)为y(n)的Fourier变换;其中,
(3)
将p(wi)进行归一化得到pi:
(4)
则功率谱熵计算如下:
(5)
设置L的搜索范围为[a,b],步长为n1,T的搜索范围为[c,d],步长为n2,将L和T可能的取值进行排列组合并生成“网格”,定义基于功率谱熵的参数优化评价准则如下:
(6)
2 EEWT降噪理论
2.1 EWT基础
EWT对信号f(t)的频谱进行自适应分割,然后构造正交滤波器组将f(t)分解为AM-FM分量。EWT的细节系数W(n,t)计算如下:
(7)

EWT的近似系数W(0,t)如下:
(8)

EWT的信号重建公式如下:
(9)
式中,*为卷积算子。AM-FM分量的表达式为:
f0(t)=W(0,t)*φ1(t)
(10)
fk(t)=W(k,t)*ψk(t)
(11)
式中,k为AM-FM分量的序号。
2.2 EWT有效边界划分方法
利用EWT分解轴承滚珠振动信号时,需要合理划分振动信号的频谱边界,只有频谱边界划分合理才能分离有效的AM-FM分量和噪声干扰。现场采集到的轴承滚珠振动信号会受到环境噪声影响,噪声的谱密度在整个频域均匀分布,且频率幅值比有效AM-FM分量的幅值小[14],因此可以根据信号的频谱幅值进行合理的边界划分。由于轴承滚珠振动信号的整个频带均受到噪声干扰,若直接分析振动信号频谱,则得到的极大值个数较多,极易引发边界误划分。Fourier频谱对噪声比较敏感,较容易出现伪“局部极大值”,但噪声能量在整个频域上是均匀分布的,因此本文首先采用Teager能量算子方法[15]对信号频谱能量进行集中,对于离散信号f(n),频谱进行能量集中计算为:
(12)

频谱能量集中后,本文分析轴承滚珠振动信号的频谱包络极大值,由于噪声的频谱包络极大值较小且相互接近,因此可将AM-FM分量的频谱包络极大值视为数据异常值,异常值即作为频谱划分的边界。本文提出一种新的有效频谱边界划分方法:四分差法。四分差法将数据按大小顺序4等分,3个分点处的数值分别为q1、q2、q3。q3与q1之差记作iq,根据iq可设定数据的上限和下限,在上下限之外的数据记作异常值,上下限计算为:
up=q3+1.5(q3-q1)
(13)
lo=q3-1.5(q3-q1)
(14)
本文提出的EWT有效边界划分方法具体步骤如下:
步骤1:对轴承滚珠振动信号作Fourier变换,得到信号频谱,采用Teager算子对频谱能量进行集中;
步骤2:信号频谱极大值记作h(s),利用三次样条插值得到包络线e(s),e(s)的极大值记作eh(s);

图1 四分差法频谱检测
步骤3:由式(13)和式(14)检测出eh(s)的异常值,进而完成边界划分,执行EWT分解。四分差法例子如图1所示,图中5个有效频带,up以上的极值也为5个。
2.3 分量筛选指标
峭度对冲击信号敏感,但忽略了轴承振动信号的循环平稳性,为有效保留信号的故障冲击信息,提出一种分量筛选指标IK用于有效AM-FM分量的选取,如下:
IK=η1Kw+η2Kc
(15)
式中,0<η1、η2<1为比例系数;η1+η2=1;Kw为加权峭度,综合考虑了峭度和相关系数两个指标,定义如下:
Kw=K·|C|
(16)
式中,
(17)
(18)
式中,K为信号x的峭度;N为信号x的长度;C为AM-FM分量与原始信号之间的相关系数;Kc为合成峭度,定义如下:
(19)
式中,se为信号包络谱;p为包络谱采样点数。η1、η2为确定采用网格搜索算法,以局部极小包络熵作为适应度值,搜寻η1和η2的最优组合。经过多次试验验证,选择IK值较大的前4个分量进行重构。
3 EMCKD- EEWT轴承滚珠故障检测方法
为解决噪声环境下轴承滚珠故障信号微弱的问题,本文提出了一种EMCKD-EEWT的轴承滚珠微弱故障检测方法,具体步骤如下:
步骤1:采集轴承滚珠故障振动信号;
步骤2:设定MCKD中L、T的搜索范围以及步长;
步骤3:对两个参数使用网格搜索法进行参数寻优,采用功率谱熵评价准则确定最优参数;
步骤4:使用EMCKD对信号进行初次降噪;
步骤5:利用EEWT将信号分解为AM-FM分量;
步骤6:利用分量筛选指标对AM-FM分量重构;
步骤7:对重构后的信号进行功率谱分析,进而检测轴承滚珠故障。
轴承滚珠故障检测流程如图2所示。

图2 轴承滚珠故障检测流程
4 试验验证-基于Spectra Quest试验台
4.1 试验装置及结果分析
为验证EMCKD-EEWT方法的有效性,采用Spectra Quest轴承试验台进行试验分析,轴承试验台如图3所示。

图3 Spectra Quest轴承试验台
轴承试验台由电机、负载、加速度传感器和转轴等组成,传感器测量方向为径向,采用文献[16-17]的策略,采用电火花技术对轴承滚珠加工单点损伤,损伤直径为0.15 mm(微弱故障)。试验轴承型号为SKF6205,电机转频约29.2 Hz,采样频率为12 kHz。轴承节径为39.04 mm,有9个直径为7.94 mm的滚珠。根据以上信息计算后,得到轴承滚珠故障频率约为141.1 Hz。轴承滚珠故障振动信号的时域波形和功率谱图如图4所示。

(a) 轴承滚珠振动信号时域波形 (b) 轴承滚珠振动信号功率谱图
图4a和图4b分别为轴承滚珠故障振动信号的时域图和功率谱图,可以看出时域信号杂乱无章,功率谱中难以找到有效故障信息。为了从微弱的故障信号中提取故障特征,首先采用EMCKD方法对信号进行初步降噪。首先根据式(1)计算得到T的理论值为85,T的搜索范围设置为[83,87],步长为1,L的搜索范围设置为[100,500],步长为5,基于功率谱熵评价准则,使用网格搜索法得到优化参数为[T,L]=[87,460],采用EMCKD处理后的功率谱如图5所示。
从图中可以发现故障频率的1/3倍频46.88 Hz和转频29.2 Hz,但是在图5中并没有直接发现故障频率,因此为了得到更理想的结果,将采用EEWT进一步处理。
首先利用EEWT将信号自动分解为AM-FM模态分量,EEWT谱边界划分如图6所示。

图5 EMCKD处理后的功率谱 图6 EEWT谱边界划分
各AM-FM模态分量的筛选指标值如表1所示。

表1 各AM-FM模态分量的筛选指标

图7 EEWT处理后的滚珠故障信号功率谱
利用筛选指标对AM-FM模态分量进行重构,重构后信号的功率谱如图7所示。
从图中可以明显发现转频的1/4倍频5.859 Hz,故障频率140.6 Hz及2倍频281.3 Hz,可以看出本文所提方法对滚珠微弱故障信号可以进行准确的提取。
4.2 对比分析

图8 EMCKD-AEWT处理后滚珠故障信号功率谱
为了验证本文所提EMCKD-EEWT算法的有效性,首先与文献[18]提出的自适应边界分割经验小波变换(AEWT)进行对比分析,降噪前处理都为EMCKD方法,EMCKD-AEWT算法处理后信号的功率谱如图8所示。
由图可知,经EMCKD-AEWT处理后的滚珠故障信号功率谱故障信号特征仍较为微弱。AEWT的谱边界划分如图9所示。
由图可知,AVMD方法的谱边界划分个数远多于EVMD,原因可能是AVMD受噪声影响较大导致错误划分。其次再与文献[19]提出的频谱包络改进的EWT方法(IEWT)进行对比分析,降噪前处理都为EMCKD方法,EMCKD-IEWT算法处理后信号的功率谱如图10所示。

图9 AEWT谱边界划分 图10 EMCKD-IEWT算法处理后的滚珠故障信号功率谱
从图中可以看出,经EMCKD-IEWT算法处理后的滚珠故障信号功率谱可以提取出1/4倍转频,以及故障频率140.6 Hz及其1/3倍频46.88 Hz,但是相较于图7可以看出,本文所提方法处理后的信号功率谱图中噪声的频率分量更少,而且故障频率及其倍频分量的提取效果更加明显。
5 试验验证-基于QPZZ-Ⅱ故障模拟实验台
为进一步验证本文提出方法对于提取轴承滚珠微弱故障的有效性,采用QPZZ-Ⅱ故障模拟实验台的轴承滚珠故障信号进行分析。轴承型号为N205,节径为39 mm,有13个直径为7.5 mm的滚珠,转速为1500 r/min,采样频率为12 kHz。轴承滚珠故障通过激光在滚动体表面加工直径为 0.1 mm,深度为 0.1 mm 的凹坑,经计算故障特征频率f0约125.2 Hz,转频fr约25 Hz。QPZZ-Ⅱ系统轴承故障实验台如图11所示。

图11 QPZZ-Ⅱ系统轴承故障实验台
轴承滚珠故障振动信号的时域波形和功率谱如图12所示。

(a) 滚珠振动信号时域波形图 (b) 轴承滚珠振动信号功率谱图
由图12a可以看出,时域波形中包含强烈的噪声干扰,没有明显关于故障信息的周期性成分,而在图12b的功率谱中,只有转频及转频的2倍频,其他频率分量幅值相对微弱,为了从微弱的故障信息中提取故障特征,采用本文所提方法进一步处理。
首先采用EMCKD方法对信号进行初步降噪。经计算得到T的理论值为96,因此设置T的搜索范围为[94,98],步长为1,L的取值范围为[100,500],步长为5,按照功率谱熵最小原则,得到优化参数为[97,175],采用EMCKD处理后得到的功率谱如图13所示。
由图13可知,幅值最大的频率分量为故障频率的1/3倍频,第2大频率分量为转频23.44 Hz。然后利用EEWT将信号自动分解为不同频段的AM-FM模态分量,限于文章篇幅,只列出利用分量筛选指标对AM-FM模态分量重构后的功率谱,如图14所示。

图13 EMCKD处理后的功率谱 图14 EEWT处理后的滚珠故障信号功率谱
由图14可知,经EEWT处理后的信号功率谱中,可以发现1/4转频5.859 Hz,故障特征频率123 Hz及2倍频246.1 Hz,从而可以对轴承滚珠故障进行准确的检测。
为进一步验证本文提出的EMCKD-EEWT算法的有效性,首先与文献[20]提出的基于能量熵优化的MCKD算法(SMCKD)进行对比,经SMCKD-EEWT算法处理后信号的功率谱如图15所示。
由图15可知,SMCKD-EEWT算法处理后的滚珠故障信号功率谱只能提取到转频,功率谱图中分布着大量噪声的频率分量,对于故障特征的提取没有太大帮助。
其次再与文献[21]提出的Shannon能量优化的MCKD算法(OMCKD)进行对比分析,OMCKD-EEWT算法处理后信号的功率谱如图16所示。
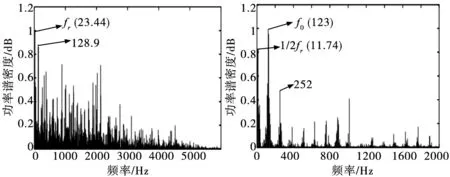
图15 SMCKD-EEWT处理后的滚珠故障信号功率谱 图16 OMCKD-EEWT处理后的滚珠故障信号功率谱
图16显示了经OMCKD-EEWT处理后的滚珠故障信号功率谱可提取到故障频率123 Hz以及1/2倍转频分量,但是对于噪声的抑制相对弱一些,而且对于倍频的提取效果并不理想,证实了本文所提方法的优越性。
6 结束语
本文提出一种EEWT结合EMCKD的轴承滚珠故障检测方法。首先利用EMCKD对振动信号进行处理;然后利用EEWT将信号分解为不同频段的AM-FM分量并利用分量筛选指标对分量进行重构;最后对重构信号进行功率谱分析,从而实现轴承滚珠微弱故障特征提取和故障检测。主要研究结论如下:
(1)本文所提EEWT方法通过四分差法有效划分轴承振动信号的频谱边界,一定程度上缓解了EWT的过分解问题;
(2)筛选指标综合考虑了峭度和相关系数两个指标,能有效筛选AM-FM分量;
(3)功率谱熵作为MCKD参数选取的评价准则,在考虑到实际与理论差异的情况下对滤波器阶数以及冲击信号周期进行了自适应选取,提升了MCKD算法对微弱故障信号增强的效果;
此外,下一步的研究方向是探索EWT更为有效的频谱边界划分方法和MCKD更有效的参数确定算法。
