面向轴承剩余寿命预测的自适应退化阶段辨识方法

2022-12-21邬世龙

组合机床与自动化加工技术 2022年12期

邬世龙

(重庆大学机械与运载工程学院，重庆 400044)

0 引言

近年来，国内外众多专家学者对滚动轴承的数据驱动式剩余使用寿命(RUL)预测方法进行大量的研究，其研究内容主要集中在轴承性能衰退指数(DI)的构建以及退化模型的建立方面，而对退化阶段的识别涉及不多。作为典型的数据驱动的DI构建方法，自编码器(Autoencoder)被广泛应用到轴承的DI构建中。HASANI等[1]通过自编码器(AE)构建了轴承的DI。KAJI等[2]提出一种基于卷积自编码器(CAE)的DI构建方法。HEMMER等[3]开发了一种利用条件变分自编码器(CVAE)构建低速轴承DI的新方法，该方法可以无监督的构建轴承的DI。尽管基于自编码器的重构模型能无监督地提取轴承退化特征，但其核心是对高维输入信号的非线性压缩，难以保证压缩特征对轴承退化状态的表征性能，且以最小重构误差为目标函数的重构模型往往对输入信号中的有用信息与噪声进行无区别重构，难以保证退化特征对退化状态的敏感性。

在轴承退化阶段辨识方面，大多文献采用了经验值、退化趋势观测及3σ原则等主观确定法，以及模型二分类法，将轴承退化阶段大致划分为正常状态阶段与退化状态阶段。张全德等[4]将VMD分解与隐马尔可夫模型(HMM)相结合，实现了轴承运行状态识别。WANG等[5]过形式化定义广义无量纲DI。ZHANG等[6]等采用波形熵来划分了轴承正常状态与退化状态。朱朔等[7]将小波核函数和支持向量数据描述(SVDD)相结合，实现了轴承退化状态的划分与评估。柏林等[8]通过3σ原则实现轴承退化阶段辨识。ZHU等[9]利用HMM根据观测数据预测其隐藏状态的能力，进行了轴承退化阶段辨识。要指出的是，上述文献中轴承退化阶段辨识方法存在较大的人为主观性，缺乏对工况环境变化的鲁棒性，且未涉及轴承失效阈值的设置。

针对以上问题，本文提出了基于互信息卷积神经网络 (mutual information convolutional neural network，MICNN)模型的DI构建方法与基于自适应超阈值波峰(adaptive peak-over-threshold，APOT)与失效概率逻辑回归的退化阶段辨识方法，并在此基础上对轴承RUL进行了全阶时间幂灰色预测，有效提高了轴承退化评估的科学客观性与寿命预测的工程可操作性。

1 基于MICNN的DI构建

基于数据驱动的轴承剩余寿命预测的关键之一在于构建能表征轴承性能衰退的退化指数。为了保证退化特征对轴承健康状态的表征能力及退化指数对状态演化的敏感性，本文提出了基于MICNN的轴承退化特征提取方法，并结合向量数据描述进行轴承DI构建。MICNN网络模型如图1所示。原始频域信号x经特征提取器C1压缩为16个通道8×1的隐层特征f，其中C1包含5个卷积层和5个池化层，第一层采用16×1的宽卷积核，步长设置为5，其余层卷积核大小均为3×1，激活函数采用LeakyRelu函数，池化层采用最大池化，步长为2；隐层特征f经特征提取器C2压缩为16维的退化特征z，其中C2包含2个卷积层和1个池化层，卷积核大小为3×1，激活函数为LeakyRelu函数，池化层采用全局最大池化。

MICNN模型可划分为两个子模块，第一个子模块为全局互信息最大化模块，即使退化特征z与原始信号x之间的互信息最大。通过洗牌操作[10]，即在大小为64的batch内将原始信号x随机打乱得到xs，然后通过与退化特征z拼接分别构建正例对[z,x]和负例对[z,xs]。鉴于原始信号x的高维度不利于网络的稳定训练和收敛且x最终被压缩为z，因此以z代替x来构建正、负例对[z,z]与[z,zs]。结合TAXD等[11]提出的基于判别网络的互信息最大化估计方法，采用全局判别器T1对正负例对进行判别，以实现全局互信息最大化，该模块的训练损失函数为：

L1=-max(EJz,x[log(T1(z,x))]+
EMz,x[log(1-T1(z,xs))])

(1)

式中，T1(*)表示引入的全局判别网络T1的输出；Jz,x与Mz,x分别表示z与x的联合分布与边缘分布乘积。

第二个子模块为局部互信息最大化模块，即使退化特征z与隐层特征f之间的互信息最大。并采用与全局互信息最大化模块相同的操作实现局部互信息最大化，该模块的训练损失函数为：

L2=-max(EJz,f[log(T2(z,f))]+
EMz,f[log(1-T2(z,fs))])

(2)

式中，T2(*)表示引入的局部判别网络T2的输出；Jz,f与Mz,f分别表示z与f的联合分布与边缘分布乘积。综合以上两个子模块，MICNN模型总的损失函数为：

L=αL1+βL2

(3)

式中，α、β为损失之间的权重。本文取α=0.1，β=1.0。整个模型采用Adam算法进行损失函数的优化，学习率和迭代次数分别为0.001与500。

图1 基于MICNN的DI构建

2 自适应退化阶段辨识与寿命预测

2.1 基于APOT的自适应退化起始点确定

POT(peaks-over-threshold)模型对观测值中超过某一较大阈值的极值数据进行拟合建模，可实现极端事件发生的风险概率评估。对i个独立同分布的随机变量X1、X2、…、Xi，总体分布函数为F(x)，则超过一定阈值u的随机变量X的超额分布函数，在u足够大时可以近似为一个广义帕累托分布(GPD)，即：

(4)

式中，ξ为位置参数；β为尺度参数。通过拟合GPD分布，可得到尾部概率为q下预警阈值：

(5)

由于工况环境的波动与轴承的性能会造成轴承的DI不具有一定短时趋势性，不满足独立同分布条件，因此可首先对退化指数序列进行滑窗去均值处理，令：

(6)

(7)

2.2 基于逻辑回归的阈值设定

逻辑回归是一种通过在底层逻辑函数估计事件发生概率的统计方法，常用于建立我们想要预测因变量和特征自变量之间的关系，其表达公式为：

(8)

式中，xi、yi分别为自变量与因变值，本文中分别指轴承DI指数与轴承的健康状态；yi=0为轴承处于健康正常状态；yi=1为轴承已进入退化或失效状态；Pi为事情发生概率，文中指轴承非正常状态的概率(取值在0～1之间)；α为回归截距；β为回归系数。式(8)给出了yi=1下的条件概率，因此在同等条件下yi=0的条件概率为Pi(yi=0|xi)=1-pi，则观测值的概率为：

(9)

取其对数似然函数作为逻辑回归模型的目标函数：

(10)

(11)

2.3 寿命预测

轴承的性能退化受多因素影响，每个因素对其RUL的影响是未知不确定的，其性能退化问题本身就存在于一个灰色系统中，本文以轴承各自的退化阶段指数为数据驱动，采用的全阶时间幂灰色预测模型[13]建立轴承退化模型并进行RUL预测，图2给出了自适应退化阶段辨识与剩余寿命预测流程图，具体步骤如下：

步骤1：DI滑窗去趋势处理：计算每个滑窗内DI均值mi，采用式(6)对DI序列进行去短时趋势处理，得到随机变量Xi。

步骤3：统计连续退化预警值数量，若数量小于5，则退回到步骤1；若数量大于等于5，则输出连续预警值的第一个值DIs，作为APOT设置的退化起始点。

步骤4：将各轴承DI序列输入APOT模型确定轴承退化起始点，从而将轴承划分为正常状态DI与退化状态DI，用于构建逻辑回归模型。

步骤5：基于构建好的逻辑回归模型，通过最大化目标函数式(10)求解出参数α，β。令P=0.95，表征轴承失效并反解出失效阈值DIe。

(12)

式中，a为发展系数；bi(i=1,2,…,h)为灰色作用量；h为时间幂项阶数；c为常数。这些参数可自适应地根据性能退化指数序列动态变化以适应退化轨迹的波动变化。

(13)

图2 自适应退化阶段辨识与RUL预测

3 实验验证

3.1 数据描述

为了验证本文方法的有效性，采用某大学提供的滚动轴承加速度寿命XJTU-SY数据集[14]进行验证。该数据集包含15个型号为LDK UER204的滚动轴承在整个使用寿命内的实际退化加速度数据，通过水平与垂直方向2个加速度传感器采集得到，采样频率为25.6 kHz，采样时间间隔为1 min，每次采样时间为1.28 s。本文利用水平加速度振动信号，选取轴承1_3、1_4、1_5、2_3、2_4、2_5、3_3、3_4、3_5共9个轴承的状态监测数据作为本文的验证数据集。

3.2 DI构建

选取每组采集数据的前2056个点作为信号样本，将各轴承样本信号的频谱作为MICNN模型输入，构建轴承各自DI序列，并采用长度l=10的滑动窗口进行平滑降噪处理。图3a给出轴承1_3的MICNN训练结果，可以看出随着迭代次数的增加，损失函数值逐渐减小，当迭代次数超过250时达到收敛。图3b给出了轴承1_3的DI构建结果，DI指数在轴承前期正常状态下无显著变化，后期进入退化阶段后，DI指数显著上升，较好呈现了轴承的性能退化规律。

(a) 损失函数收敛曲线 (b) 轴承1_3DI曲线

为了验证本文提出的MICNN模型在退化特征提取方面的优越性，在同等数据支撑条件下使用自编码器(AE)、卷积自编码器(CAE)、变分自编码器(VAE)3种常见的DI构建模型进行比较，并应用文献[15]中提出的单调性(Mon)、相关性(Corr)、鲁棒性(Rob)和综合指数(CI)4个评价指标对4种模型所构建的轴承1_3的DI进行进一步的定量评估，如图4所示。

(a) DI曲线对比 (b) DI得分对比

从图4可以看出基于MICNN模型构建的DI的单调性、相关性、鲁棒性和综合指数均大于AE、CAE和VAE模型。可以发现，MICNN模型通过最大化退化特征z和原始信号x间的互信息及退化特征z与隐层特征f间的互信息，能够最大程度保证退化特征与原始信号间的信息关联性，从而使得MICNN模型构建的DI更能有效地表征轴承的性能退化状态。

3.3 自适应退化阶段辨识

图5 不同方法退化起始点结果

根据2.3节中的步骤1～步骤3，采用APOT模型对图3b中的DI序列进行退化起始点检测，结果如图5所示，轴承在64 min进入退化状态。为了证明APOT模型的优越性，分别采用基于SVDD超球体半径、3σ原则、隐马尔科夫模型(HMM)对图3b中的DI序列进行退化起始点检测，结果如图5所示。从图5可以看出，采用APOT模型检测出的起始退化点早于其余3种方法检测的退化起始点，对轴承退化状态更敏感。根据步骤4～步骤5，可得测试轴承1_3的逻辑回归参数α和β的估计值分别为-31.13，44.93，对应的失效阈值为0.69。表1给出了采用本文方法得到的各测试轴承的自适应退化阶段辨识结果。由于轴承工况环境的不同，其退化阶段存在较大差距，即使是统一工况下的测试轴承由于个体退化轨迹的差异性，其退化阶段也不尽相同。可见，根据轴承自身退化规律进行无参考的退化阶段识别的必要性。

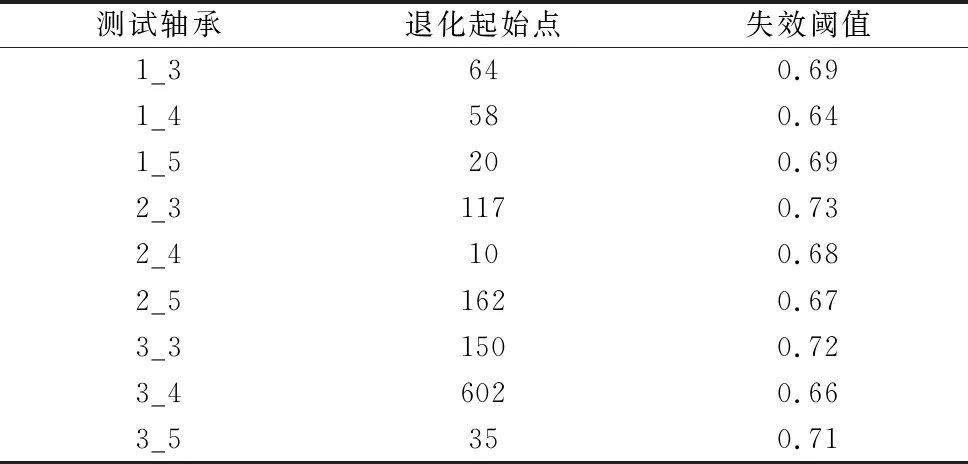
表1 测试轴承退化阶段辨识结果

3.4 RUL预测

为了验证本文自适应退化阶段辨识方法在轴承剩余寿命预测方面的有效性，基于以上4种不同退化阶段辨识方法，采用全阶时间幂灰色预测模型对测试轴承进行RUL预测。轴承1_3、2_5与3_5的剩余寿命预测结果如图6所示。

(a) 1_3 (b)2_5

从图6可以看出相较于另外3种方法，本文方法对轴承退化阶段辨识更加敏感，且基于本文方法得到的剩余寿命预测结果更接近真实值，说明本文方法对轴承退化阶段的辨识更加客观，且在轴承剩余寿命预测方面更具优越性。

为了进一步验证本文方法的优越，对所有测试轴承的预测结果进行打分：

Ei=actRULi-RULi/actRULi

(14)

(15)

(16)

式中，actRULi、RULi、Ei和Ai分别为第i个测试轴承的实际寿命、预测寿命、误差率和分数。将得分与文献[16]中采用的SAE+LSTM与SAE+BiLSTM方法进行比较，结果如表2所示。从表2可以看出，本文的得分与预测误差的标准差均优于文献[16]中的2种方法，说明本文方法对轴承剩余寿命的预测更具稳定性，且精度更高。