疫情冲击下中国股市投资策略构建——基于复杂网络视角

洪振木，赵 杰

（安徽财经大学金融学院，安徽蚌埠 233030）

股票市场由众多相互关联的个体构成，通常被认为是一个典型的复杂系统，股票市场中不同行业之间也存在着聚集现象，使得重大突发事件带来的风险迅速蔓延至整个股票市场。2019年12月新型冠状病毒开始在我国境内扩散，引发了金融市场的大幅震荡〔1〕。作为金融市场的核心组成部分，股票市场在疫情冲击下的整体结构变化以及投资组合优化无疑是众多投资者和投资机构最为关心的问题。

复杂网络理论自20世纪图论诞生以来被众多专家学者用来描述含有相互作用的实际系统，利用个体之间的某种联系将节点连接成一个网络，通过研究网络的特性来反映实际系统的特点和系统中个体之间的作用关系。这种描述方法早期更多地应用于描述实际系统整体的网络拓扑性质，揭示系统中的网络关系，关沫等〔2〕通过Internet监测数据和统计手段证实了Internet是一种同时具有“小世界”和“无尺度”网络特征的复杂网络。Onnela等〔3〕基于复杂网络的视角对股票关联网络的基本拓扑统计性质进行了分析。张来军等〔4〕通过分析股票关联网络特性得出股票指标之间的关联性。近年来越来越多经济管理领域的专家学者利用复杂网络对金融市场进行建模，分析投资风险在股票市场中的传导机制，优化投资组合。谢赤等〔5〕利用随机矩阵理论和相关系数动态演化模型对所选取的数据进行优化，利用阈值法解释风险在网络中的传染效应；陈超洋等〔6〕归纳了构建网络模型的算法和系统性风险的测度方法，并基于复杂网络视角对系统性风险的难点问题进行了展望。李爱忠等〔7〕分析了非系统性风险以网络形式进行传染、溢出和蔓延等现象。

在全球化影响下，世界各国在政治、经济等领域间的联系越来越密切，国家和地区间的资金流动存在着一定程度的相关性〔8〕，使得诸如金融危机和新冠疫情等重大突发事件能够迅速在世界范围内产生影响。对于2008年金融危机给我国股票市场带来的影响，Yan等〔9〕用复杂网络分析了美国次贷危机冲击下中国金融市场的稳定性；秦春雷等〔10〕分别从宏观和微观的角度分析金融危机影响下证券市场复杂网络特性随时间变化特点，采用移动窗口的方法对股票市场的变化进行动态研究；谢赤等〔11〕利用滑窗分析法构建关联网络，从网络节点和连边变化角度研究金融危机前后股票市场的变化，并利用仿真模拟冲击研究股票市场受到重大冲击时的变化和股票市场的稳健性；冯霞等〔12〕在分析航空网络鲁棒性时使用仿真攻击的方法；李延双等〔13〕则将仿真攻击应用到分析股灾的外生冲击对中国股市网络的影响；刘超等〔14〕利用复杂网络分析了金融危机期间中国同业拆借市场的相关特性以及在应对金融危机时同业拆借市场利率所表现出来的市场性和稳定性。对于此次新冠疫情对金融市场的影响，方意等〔15〕基于带有动态窗口期的事件分析法分析了新冠疫情会对金融市场的风险带来显著的影响，并结合系统性风险的理论框架，针对突发性政策事件提出政策建议；徐宏等〔16〕采用事件研究法分析了新冠疫情对中国股票市场的影响。目前已有的研究大多侧重于分析在疫情冲击下的股价波动性、利用复杂网络从理论层面研究股票市场或金融市场网络结构，缺乏对系统的分析和具体投资策略的研究。

本文在新冠疫情冲击背景下，从复杂网络视角出发构建投资组合。边际贡献主要有：（1）从疫情冲击前后股票收益率相关系数矩阵中提取每只股票与市场中其他股票之间的相关系数向量，计算两个时期同一股票对应的相关系数向量之间的欧氏距离，以此度量该股票在受疫情影响前后与其他股票之间连接性变化，进而反映股票市场受到冲击时各股票节点的稳定性；（2）利用GN算法对股票关联网络进行社团划分，将股票欧氏距离和社团划分相结合，以分散风险为原则进行投资策略的优化。

1 研究方法与模型设定

在股票关联网络中以股票个体作为网络节点，节点之间的连边代表股票收益率变动的相关性大小。由于股票收益率相关系数会存在负值，所以本文将相关系数转化为“距离”来表示节点之间的相关性，由此构造股票市场的关联网络。

1.1 复杂网络的构建 选取股票日度交易数据，股票i在第t日的收盘价为P（t），可以算出股票i在不同时期的对数收益率，记为ri（t）：

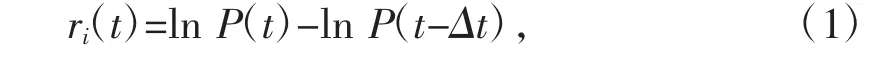
式（1）中Δt为计算收益率的时间周期（本文表示日间隔）。根据任意2只股票i和j的收益率序列计算在观测区间内股票价格波动的相关系数ρij：

式中，ri和rj分别为股票i和j的收益率序列，E［·］表示数学期望，ρij∈［-1，1］。如果2只股票之间完全正（负）相关，则ρij=±1；如果2只股票之间完全无关，则ρij=0。计算任意2只股票之间收益率相关系数构成相应的相关系数矩阵A。

相关系数矩阵A表示所选股票间收益率相关性，会出现负值元素，所以需要把相关系数矩阵转化为距离矩阵。用dij来表示股票i和j之间的距离：

由式（3）可知相关系数越大，股票之间距离越小。将距离作为构建网络的关联性指标，把距离矩阵导入Matlab软件中得到相应的MST网络。

1.2 投资组合构建

1.2.1 欧氏距离 欧氏距离也称“欧几里得度量”，它表示在M维空间中两个点之间的真实距离。本文将n个时期市场中股票对数收益率相关系数矩阵分别记为A1，A2，...，An。矩阵的每一行（或每一列）都代表着股票节点与网络中其他股票节点之间的相关关系，可以将其看作表示股票节点与整体网络的关系向量。以其中以1只股票G为例，每个周期T都有对应的向量表示股票G与网络的关系。记为G=（GT1，GT2，...，GTN），GTm=（xm1，xm2，...，xmk）在股票市场从周期Tm到周期Tm+1时，股票节点与市场之间的关系发生变化，本文引用欧氏距离来度量这种变化：

根据式（4）可求得股票相关系数向量在不同时期之间的变迁距离矩阵，通过提取矩阵对角线数据来衡量同一股票在相邻周期之间的距离变化（以下简称“股票欧氏距离”）。并以此反映所选股票相对市场中同时变化的其他股票价格变化是否敏感，是否会对市场波动产生明显的结构性变化。若某只股票欧氏距离大说明股票市场受到冲击时会给该股票带来较大的影响。在进行投资组合构建时选择股票欧氏距离小的股票来降低投资风险。

1.2.2 复杂网络社团划分 选用GN算法对股票网络进行社团划分，其基本思想是通过计算出网络中相对于源节点的各节点的介数，通过删减介数最大的边将网络中的点逐渐分离出去，在达到事先设定的社团数量时停止这一过程，从而将网络划分为分离的社团。同时引入模块度Q来衡量社团划分效果，Q值越大表示社团划分效果越好。本文构建的网络属于无向网络，其Q函数表达式如下：

式中，nc是社团数量，M是整个网络的边数，lv是社团v内部所包含的边数，dv是社团v中所有节点度值之和。

2 股票关联网络的构建

2.1 数据采集预处理 选取能够近似反映中国股市涨跌情况的沪深300成分股日收盘价数据，时间为2019年3月1日—2022年3月1日，数据来源于Wind数据库。从300只股票中剔除数据连续缺失超过10 d的股票，取最终剩余的270只股票作为观测样本。在观测期间沪深300指数收益波动情况见图1。

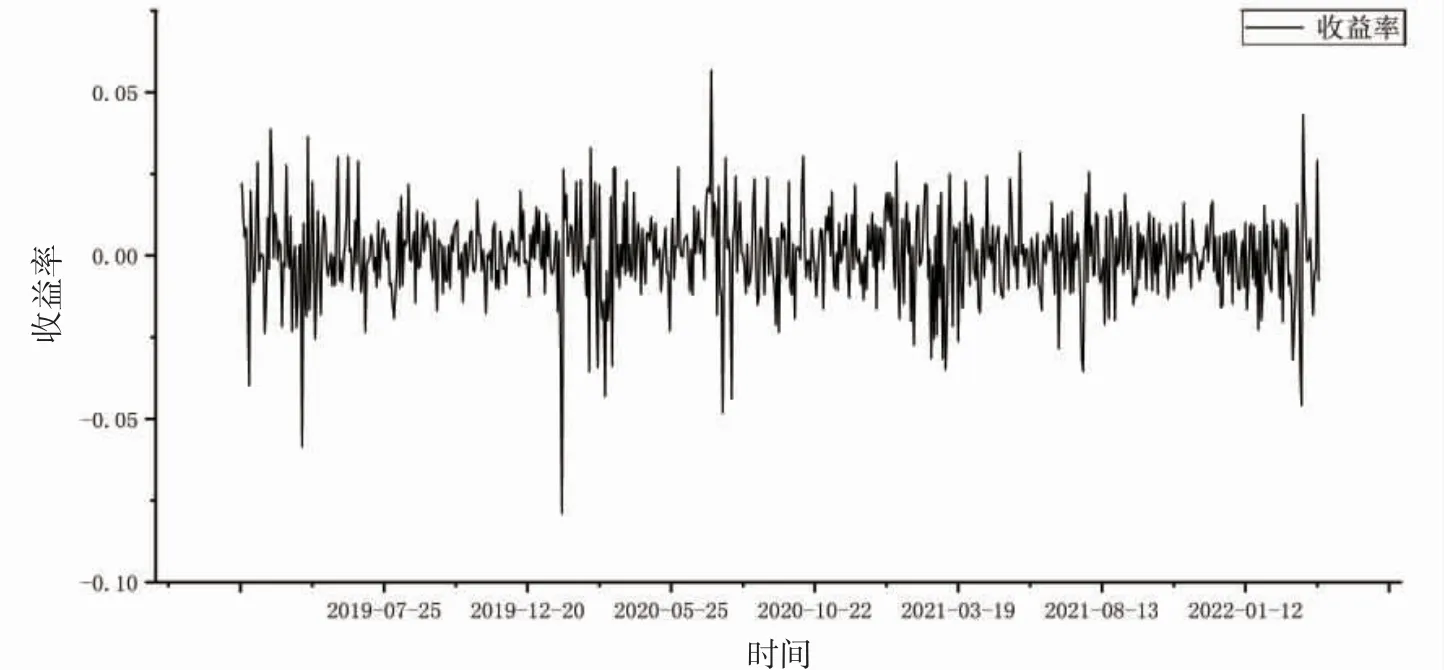
图1 沪深300指数收益率波动图

根据沪深300指数收益率波动，结合疫情发生前后产业发展情况将时间跨度模糊划分为4个阶段：第一阶段（2019年3月—2019年12月），股票市场还未受到疫情影响，投资者决策主要依据市场行情；第二阶段（2020年1月—2020年10月），疫情暴发各大产业均受到影响，投资者情绪低落，证券市场受到冲击；第三阶段（2020年11月—2021年8月），产业恢复期，产业开始复苏，投资者情绪开始好转；第四阶段（2021年9月—2022年3月），疫情基本得到控制，只在局部发生小规模的疫情感染现象，故本文将前3个阶段作为主要研究对象，利用2021年度数据来检验投资组合策略的效果。通过公式（1）、（2）和（3）对原始数据进行处理，以股票间的距离为连接依据生成对应各阶段的最小生成树网络，并通过股票欧氏距离来反映不同阶段股票的波动情况。

2.2 最小生成树形成与结构分析 利用Matlab和Pajek软件绘制复杂网络拓扑图，这里以疫情冲击后股票市场交易数据为例，得到最小生成树网络。见图2。

图2 第三阶段最小生成树网络

为了更清楚地看到股票市场关联网络的变化情况，本文对3个阶段进一步细分，将所选取的总样本时间划分为15个时间段，分别记为：P1，P2，…，P15。在计算股票相关系数的股票欧氏距离之前需要确定一个临界点，在疫情冲击影响下，该临界点前后股票市场的波动相对较大，从而消除因信息传递的时滞给研究带来的影响。分别选取2019年12月31日、2020年1月15日、2020年1月20日 和2020年1月31日作为临界点。考虑到股票市场在面对突发事件时具有一定的自我调节能力，为得到疫情冲击前后股票市场相对明显的变化，选取时间节点前后2个月的数据进行分析。分别计算4个时间节点前后不同股票欧氏距离段内对应股票数量分布情况。见图3。

图3 不同时间临界点各股票欧氏距离段内股票分布图

从图3可以看出以2020年1月20日为临界点下股票集中分布在股票欧氏距离较大的区域，反映出整个股票市场在此临界点前后波动较大。分别以4个时间节点作为临界点计算股票欧氏距离，对应均值分别为5.74、6.42、6.49和4.31，可以看出2020年1月20日为临界点时股票市场前后总体波动最为明显，且在该临界点之前股票欧氏距离呈现逐渐增大的趋势。综上所述，以2020年1月20日为临界点最能反映股票市场冲击前后变化。

3 投资策略设计与检验

3.1 股票欧氏距离分组 临界点后与临界点前的日收益率均值之差表示疫情冲击前后的收益率变化情况，以所选取时间内股票对数收益率标准差作为衡量风险的指标。为研究收益率和风险随股票欧氏距离变化的趋势，按照股票欧氏距离大小将其均匀分为10组，计算各组对数收益率的均值和标准差。结果见表1。

表1 收益率和标准差随股票欧氏距离变化表

从表1可以看出随着股票欧氏距离的增大收益率和标准差整体呈现出下降趋势，结果符合我们的预测，即股票欧氏距离越大对应股票相对于整体市场的变化就越大，所选股票对市场中同时变化的其他股票价格变化越敏感，受疫情负面影响所产生的结构性变化越明显。在股票市场受到负面冲击背景下构建投资组合时，投资者可选择股票欧氏距离小的股票来保证收益率的相对稳定。

3.2 股票关联网络社团划分 为了构建疫情影响下的股票投资组合，选取疫情突发时期（即第二阶段）的数据为依据，利用GN算法对选取的270只股票的最小生成树网络进行社团划分，得15个社团。根据式（5）求得所划分社团的模块度Q=0.879，表明利用GN算法对沪深300成分股最小生成树网络进行划分的社团结构非常清晰，经过筛选得到的270只股票较为均匀地分布在各个社团内。表2～3列举了其中2个社团。

从表2～3划分结果可以看出同一社团内会存在相同行业的股票，同一行业主营业务相近，归为同一社团，和传统按照行业进行分类有类似的地方。社团中还存在着不属于同一行业的企业，但处于同一地域或被同一股东控股。由于最小生成树网络中节点按照收益率相关性的距离进行关联，距离越小则节点之间关联性越强，最小生成树网络是由距离最小的节点之间连接而成，GN算法将网络中关联性较强的股票划分到一个社团，同一社团内股票在遇到风险时股票收益波动具有一定的协同性。所以在进行构建投资组合时，选取不同社团中的股票有利于分散投资风险。

表2 GN算法社团3划分情况

表3 GN算法社团13划分情况

3.3 投资策略与验证 综合上述实证分析结果，具体投资组合策略主要分两步：第一步，在投资者进行构建投资组合时，选择股票欧氏距离较小的股票组合；第二步，选取该股票欧式距离分组中处于不同社团的股票分散风险。当距离分组中出现多只股票位于同一社团时，选取对应股票欧氏距离最小的股票构建投资组合。以期在股票市场受到负面冲击背景下，降低投资风险。

为检验上述方法是否具有实际价值，以2019年11月20日—2020年3月20日期间的历史收盘价数据计算股票欧氏距离，根据上述方法构建投资组合A；选择股票欧氏距离较大的股票构建投资组合B；选择不同行业的股票构建投资组合C。B、C为对照组，3个组合的股票组成见表4。

表4 投资组合内股票组成情况

计算上述投资组合2021年度收益率与标准差，利用组合收益率与标准差的比值来衡量投资组合的效果，结果见表5。

表5 2021年度投资组合收益风险情况

表5结果显示，依据投资策略构建的投资组合A相较其他投资组合在一年中具有较高的收益和较低的风险，总体投资效果较好，能够在负面冲击背景下有效分散风险。

新冠疫情的暴发给中国股市带来了负面冲击。本文选取沪深300成分股为观测样本，运用最小生成树算法构建不同时期股票市场关联网络，分析了疫情冲击下中国股市的波动情况。基于股票相关系数向量的欧式距离和股票关联网络的社团划分提出一种投资策略，通过对比实验分析了该策略的有效性。研究结论如下：（1）股票相关系数向量的股票欧氏距离随疫情的发展先上升，后下降，前后波动最大的时间临界点是2020年1月20日，相较疫情被发现的时间约延迟了20 d，说明疫情对股市的影响是逐渐增大的，信息在股市中的传播存在时滞；（2）基于股票欧氏距离大小分组的投资组合收益具有明显的变化趋势，在该投资策略指导下所做的投资组合在未来能够获得较高收益。对比实验结果表明，在该投资策略指导下，相较股票欧氏距离大的投资组合，股票欧氏距离小的投资组合具有较好的投资效果，且基于历史交易数据所做的投资组合在未来能够获得较高收益，为投资者构建投资组合提供参考。