基于二维弹性波方程的高阶NAD-SPRK算法

陈 丽，朱兴文，张朝元*

（1.大理大学工程学院，云南大理 671003；2.大理大学数学与计算机学院，云南大理 671003）

开发精度高、效率高的模拟地震波计算方法是目前涉及地震波动方程开展反演的一个重要方向。过去的计算格式〔1-5〕在进行地震波模拟时会造成严重的数值频散现象而达不到当前规模大的地震波模拟效度，杨顶辉教授团队于2003年首次在地震波正演模拟中引入近似解析离散化（nearly analytic discrete，NAD）算子〔6〕，目前已获得系列NAD算子的数值算法〔7-10〕，这些算法的模拟频散效果均很不错，然而这些算法仅为四阶的空间精度。

为提高地震波计算模拟效度，本文针对具有哈密尔顿系统的二维弹性波方程，结合离散空间高阶偏导数的八阶NAD算子和离散时间导数的二阶辛分部Runge-Kutta算法〔4，11〕，得到了八阶NADSPRK算法。针对该方法，从理论和数值计算两方面研究了其稳定性条件、数值频散和计算效率。结果表明：同四阶NSPRK算法〔11〕、八阶Lax-Wendroff（LWC）算法〔12〕和八阶交错网格（SG）算法〔12〕相比，八阶NAD-SPRK算法压制数值频散的能力显著优于传统数值计算方法，且具有最小的数值误差和最高的计算效率。

1 方法推导

设二维弹性波方程为：

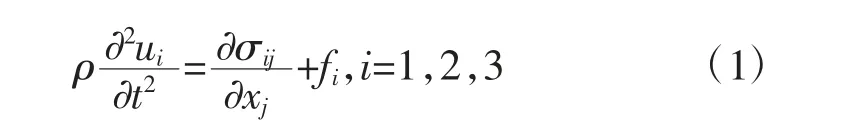
其中，j=1，3，fi和ui分别为i方向的力源分量和位移分量，ρ=ρ（x，z）为介质密度，σij为应力张量。

由应力与张力之间的物理关系，方程（1）式的向量方程为：

记vi=∂ui/∂t（i=1，2，3），则v=（v1，v2，v3）T，方程（2）式为：

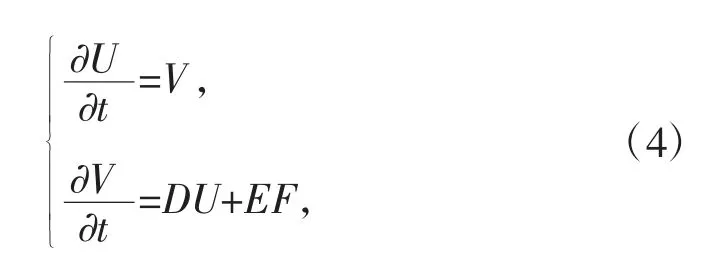
其中D称为偏微分算子矩阵，且

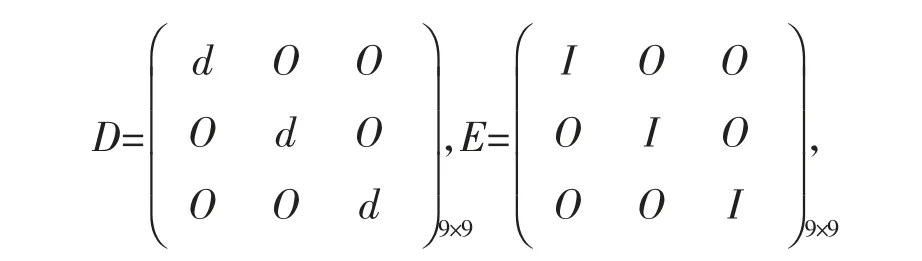
O为三阶零方阵，I为三阶单位矩阵。

此时，表达式（4）拥有哈密尔顿系统模式，故采纳哈密尔顿系统模式的求解流程对二维弹性波方程表达式（1）的对应方程（4）式进行求解。具体求解如下：

1）由于涉及位移u及粒子速度v的有关二阶、三阶等偏导数存在于高阶偏微分算子矩阵D中，因此首先需要对方程（4）式右边的D进行空间高阶偏导数离散化。逼近位移u和粒子速度v的二阶和三阶偏导数的计算公式详见文献〔12-13〕。

2）对D进行离散化处理后，表达式（4）成为关于时间的一个半离散化哈密尔顿系统模式。再采纳辛分部的二阶Runge-Kutta算法〔4，11〕对半离散化哈密尔顿系统表达式（4）进行求解，计算公式为：

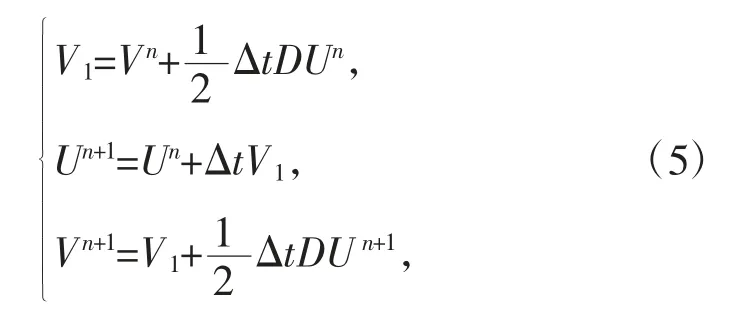
其中，△t表示时间步长，V1表示计算的中间变量。

为加快计算速度及减少存储空间，简化（5）式得到计算公式：

其中D2=D·D。

以上二维弹性波方程表达式（1）的对应求解表达式（5）和式（6）记为八阶NAD-SPRK算法。

为了揭示八阶NAD-SPRK算法在进行地震波场数值模拟时的数值频散和计算效率情况，下面从理论和数值计算两方面分析该方法的稳定性条件、数值频散关系和计算效率，并同四阶NSPRK算法、八阶LWC算法和八阶SG算法进行比较。

2 稳定性分析

在利用有限差分方法进行波场数值模拟时，为保证计算的稳定性，应该选取恰当的模拟参数，就是在选定空间增量h及波速c后，时间增量△t的选择也要达到相应的稳定条件。本文使用Fourier方法〔13〕推导出二维声波情形下八阶NAD-SPRK算法的稳定性，其稳定结果为：

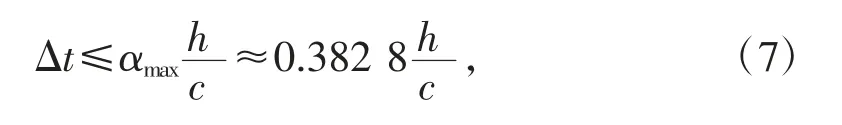
其中，h=△x=△z为空间步长，α=c△t/h为库朗数，αmax为最大库朗数。

对于弹性波情况，推导出弹性波方程数值方法的精确或解析稳定性条件通常是很复杂的〔5〕。当应

用八阶NAD-SPRK算法求解二维弹性波方程时，其稳定性条件由系数估计技术（Vichnevetsky，1979）不能直接确定，而是由声波情形下最大波速时的稳定性条件来近似代替。因此，估计时间网格尺寸应满足以下稳定性条件：

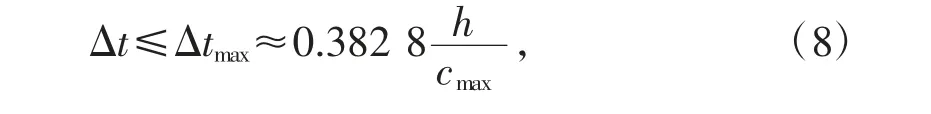
式中tmax为使八阶NAD-SPRK算法在二维弹性波情况下保持稳定的最大时间步长，cmax为最大纵波速度。

3 数值频散

下面通过模拟波场来研究八阶NAD-SPRK算法的数值频散情况。为此，本文挑选二维弹性波介质具有均匀各向同性特点的方程如下：

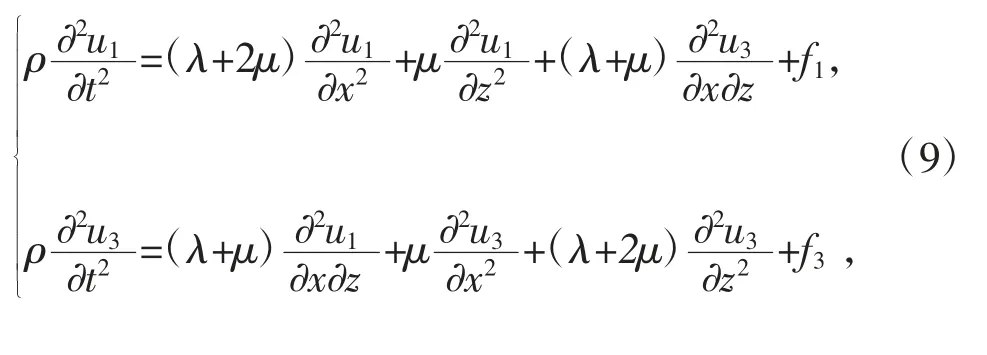
此处，u1，u3分别表示位移在方向x和方向z的分量，ρ为介质密度，λ，μ为Lame参数，f1和f3为震源函数在方向x和方向z的分量。

在数值实验中，选择模型的参数为λ＝6.0 GPa、μ＝24 GPa、ρ＝1.5 g/cm3。网格点数为301×301，空间网格步长和时间步长分别为△x＝△z=40 m和△t＝1×10-3s。震源位于计算区域中心，且Ricker子波为f0的震源函数，且f1=f（t）、f3＝0。接收器位于R（5.25 km，4.8 km）。其中，f（t）表达式为：

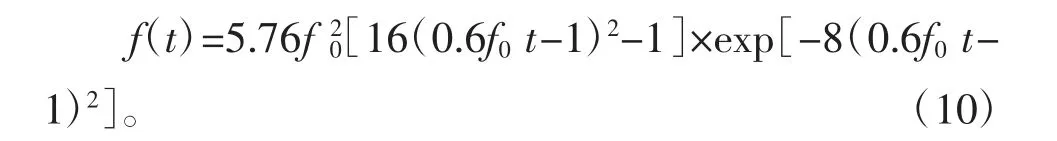
图1分别为由八阶NAD-SPRK算法、四阶NSPRK算法、八阶LWC算法和八阶SG算法通过模拟计算给出在Ricker子波频率为f0＝25 Hz下从时间t＝0 s到t＝0.68 s在接收点R处的波形记录。可以看到图1（a）、图1（b）和图1（d）的波形几乎相同，而由八阶LWC算法模拟产生的波形记录存在一定的数值频散，见图1（c）。

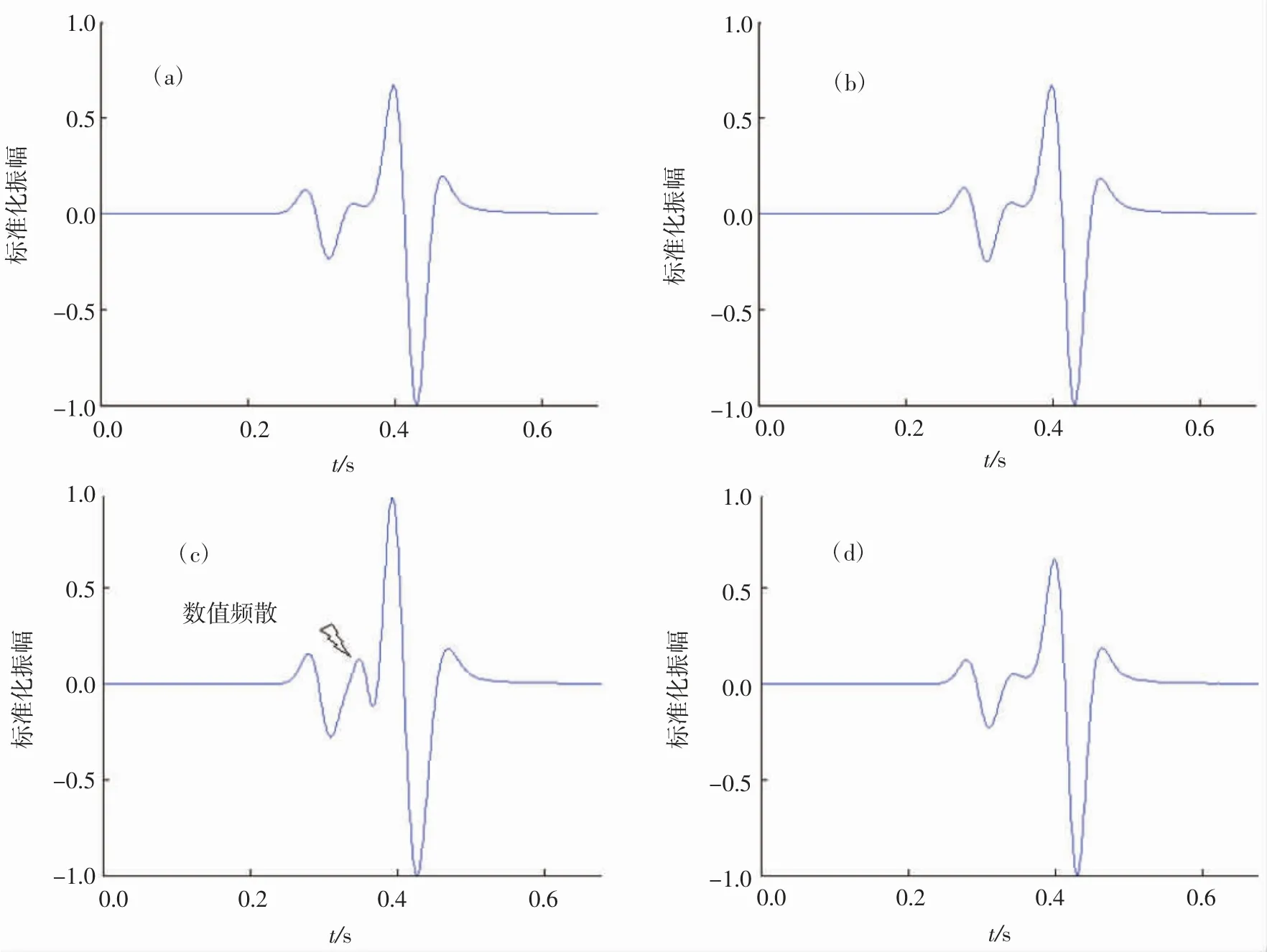
图1 4种算法模拟产生在均匀各向同性介质和频率为f0=25 Hz的Ricker子波下的波形记录

图2分别给出了由4种方法模拟产生在Ricker子波频率为f0=40 Hz下从时间t=0 s到t=0.68 s在接收器R处的波形记录。从图2（c）和图2（d）可了解到，经八阶LWC算法和八阶SG算法模拟计算出的波形记录出现严重的数值频散现象。而经八阶NAD-SPRK算法和四阶NSPRK算法计算得到的图2（a）和图2（b）的波形记录清晰，且在较高频率下数值频散不明显。尤其是由八阶NAD-SPRK算法计算得到的图2（a）在如此高的频率情况下几乎没有可见的数值频散。结果表明，八阶NAD-SPRK算法在抑制数值频散方面比八阶LWC算法和八阶SG算法更有效。

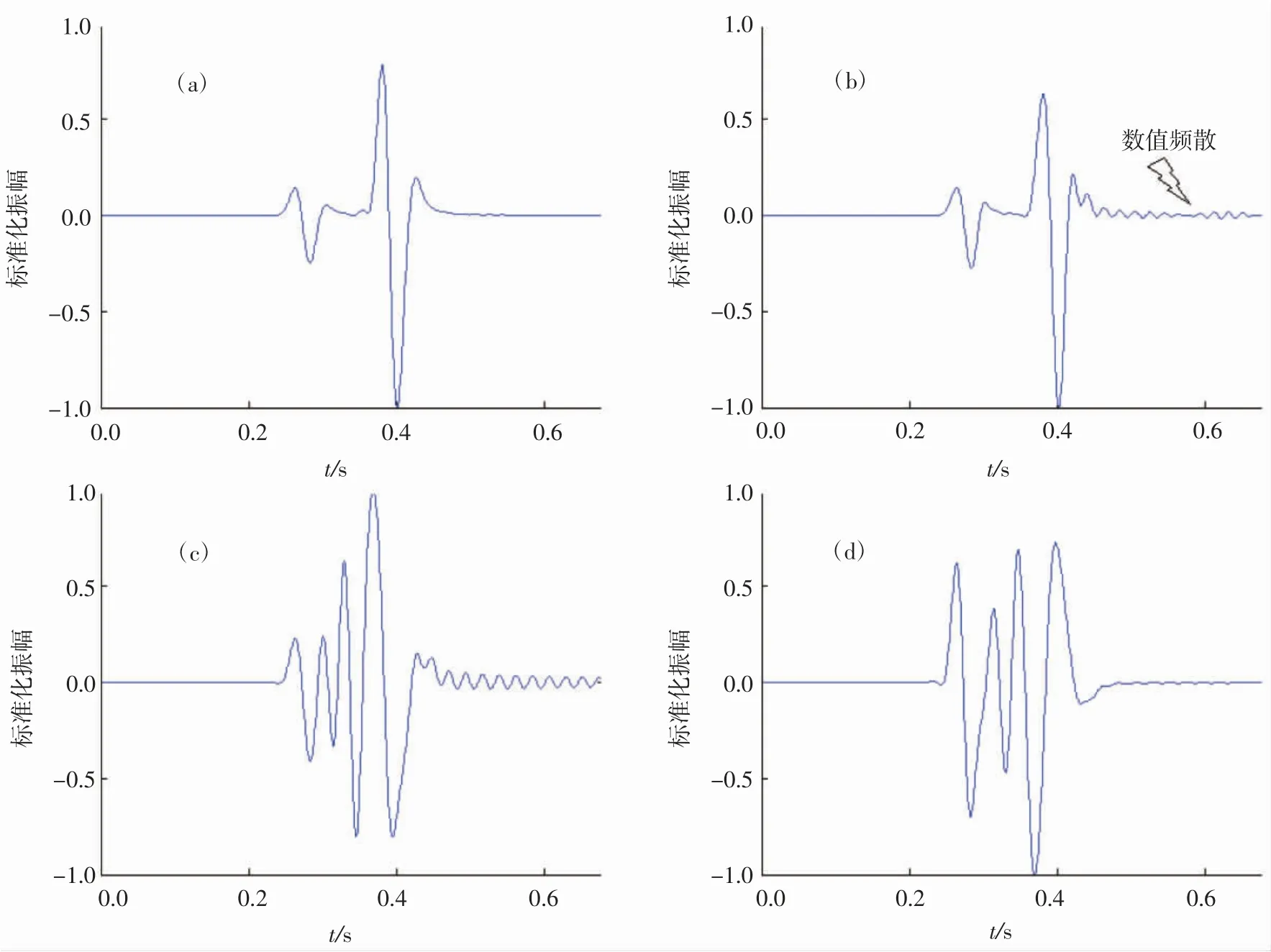
图2 4种算法模拟产生在均匀各向同性介质和频率为f0=40 Hz的Ricker子波下的波形记录

4 计算效率

此部分，将呈现八阶NAD-SPRK算法数值计算的模拟结果，也展示该方法数值计算的模拟效率。此处，同样选择介质具有均匀各向同性特点的二维弹性波表达式（9）。

此实验中，模型的参数为λ=4.704 GPa、μ=8.4 GPa和ρ=2.1 g/cm3。网格点数为301×301，空间网格步长和时间步长分别为△x=△z=40 m和△t=0.004 s。震源位于计算区域中心，震源函数为f0=12 Hz的Ricker子波，且f1=f（t）和f3=0。

图3分别为粗网格（△x=△z=40 m）下由八阶NAD-SPRK算法和八阶LWC算法在t=1.6 s时刻产生的水平位移方向和垂直位移方向的波场瞬时快照。从图3可知用这两种算法计算模拟弹性波给出的波前快照大致上是相同的。虽然在相同网格点数下，八阶NAD-SPRK算法的计算成本比八阶LWC算法高，这是由于八阶NAD-SPRK算法模拟计算时需要同时计算位移、粒子速度及其梯度等变量。但是，八阶NAD-SPRK算法模拟生成的波场快照（图3（a）（c））在空间步长为40 m时数值频散较小，而八阶LWC算法数值频散较严重（图3（b）（d））。结果表明，八阶NAD-SPRK算法能有效应用于粗网格大尺度情形下的数值模拟。

为了有效消除数值频散，在与图3有相同的库朗数条件下，由八阶LWC算法在细网格△x=△z=20 m和对应601×601的网格点数条件下在t=1.6 s时刻计算模拟出的波场快照见图4，此时没有可见的数值频散。在达到相同消除数值频散条件下，对于同一计算域，在△x=△z=40 m粗网格下，八阶NAD-SPRK算法的网格点数仅为301×301。可见，八阶NAD-SPRK算法模拟计算时所需的内存需求量约为八阶LWC算法的25.08%。

对比图3（a）（c）和图4（a）（b），本文所提出的方法在相同库朗数下，可以提供与八阶LWC算法在细网格上相同的精度，但它们的计算成本是不同的。八阶NAD-SPRK算法模拟得到图3（a）（c）所消耗的CPU时间约185 s，而八阶LWC算法模拟得到图4（a）（b）所消耗的CPU时间约293 s。这揭示在没有数值频散可见的状况下，八阶NAD-SPRK算法的计算效率约为八阶LWC算法在细网格下的1.6倍。以上实验均在Intel（R）Core（TM）2Duo CPU和内存为2.33 G的计算机环境下进行。

图3 粗网格△x=△z＝40 m下由八阶NAD-SPRK算法和八阶LWC算法生成的在t＝1.6 s时刻的波场快照

图4 八阶LWC算法在细网格△x=△z＝20 m下t＝1.6 s时刻的波场快照

为了进一步验证八阶NAD-SPRK算法的有效性，比较了八阶NAD-SPRK算法和八阶LWC算法在模拟二维弹性波方程的数值解。Dablain〔1〕的研究结果表明，在细网格条件下八阶LWC算法提供的数值结果近似等于解析解，并与伪谱方法模拟的结果相等。

八阶NAD-SPRK算法在空间网格步长和时间步长分别为△x=△z＝40 m和△t=0.004 s下模拟得到的结果与八阶LWC算法在空间和时间步长分别为△x=△z=20 m和△t=0.002 s下模拟产生的结果基本相等。图5为由八阶NAD-SPRK算法在粗网格（△x=△z=40 m）上和八阶LWC算法在细网格（△x=△z=20 m）上模拟得到的弹性波波形记录，其中图5（a）和图5（b）分别为在接收器R（6.6 km，7.6 km）处的水平位移方向和垂直位移方向的波形记录。结果表明，八阶NAD-SPRK算法针对均匀各向异性情形在粗网格条件下可以得到相等的模拟结果，并且计算量和计算机内存都大大地减少。

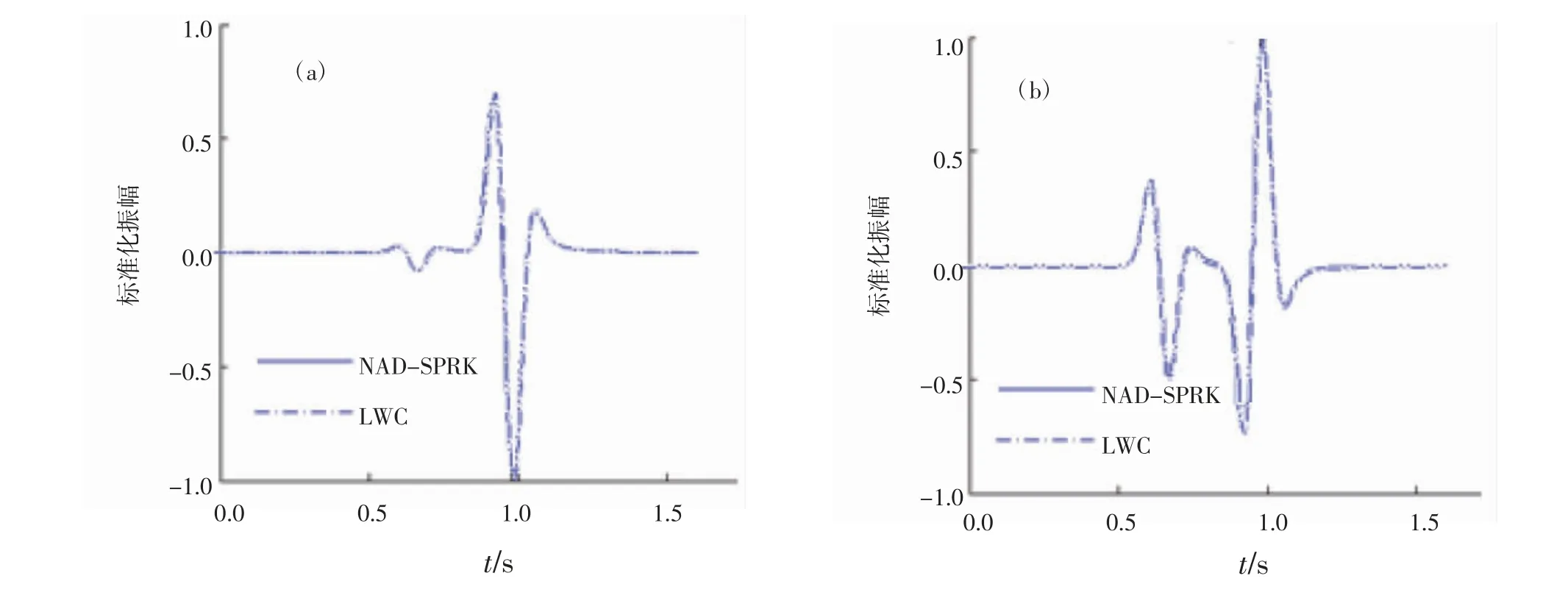
图5 细网格（△x=△z＝20 m，△t＝0.002 s）下的八阶LWC算法和粗网格（△x=△z＝40 m，△t＝0.004 s）下的八阶NAD-SPRK算法在接收器R（6.6 km，7.6 km）处位移水平方向对比的波形记录

5 结论

为使地震波数值计算的正演方法的精度更高和速度更快，本文在杨顶辉教师团队的研究基础上，针对拥有哈密尔顿特征的二维弹性波方程，结合离散空间高阶偏导数的八阶NAD算子和离散时间导数的二阶辛分部Runge-Kutta算法，推导出了一种八阶NAD-SPRK算法。结合理论和数值两角度进行了该方法的稳定性分析、数值频散探索和计算效率比较等工作。数值结果表明：同四阶NSPRK算法、八阶LWC算法和八阶SG算法相比，八阶NAD-SPRK算法在压制数值频散上明显好于传统的数值模拟方法，计算量和计算机内存也都大大地减少。在达到相同消除数值频散条件下，八阶NADSPRK算法模拟计算时所需的内存需求量约为八阶LWC算法的25.08%，计算效率约为八阶LWC算法的1.6倍。可见，八阶NAD-SPRK算法在全波形反演和波动方程的逆时偏移等问题上有望得到广泛推广和有效应用。