基于Opt LHD-RSM的汽车电连接器接触件优化

莫易敏，夏 凯，张 平

(1.武汉理工大学 机电工程学院，湖北 武汉 430070；2.中化农业生态科技(湖北)有限公司，湖北 江陵 434100)

随着汽车电气化不断发展，预估未来每辆汽车将使用600～1 000个电子连接器[1-2]。据统计，电子元器件中40%的失效是由于电连接器引起[3]。探究电连接器接触件插拔性能具有重大意义。

目前，国内外学者对电连接器接触件插拔性能进行了一定的研究。Price[4]建立了接触件插入力模型，通过试验研究了装配速度对插入力的影响规律；Angadi[5]等结合仿真与试验，研究了不同环境温度下接触表面粗糙程度、过盈量等加工参数对其接触性能的影响；Behzad[6]等运用了有限元仿真的方法，研究了振动频率、振动加速度、预应力对其接触性能的影响。孟圆[7]、骆燕燕[8]、勒方建[9]等对圆柱式电连接器接触件进行有限元仿真，研究了单次插拔下接触件各结构参数对其性能的影响规律。但是，针对汽车电连接器中常用的片式接触件的研究较少，且未考虑多次插拔循环对接触件性能的影响。此外，大多数优化仅针对某一结构参数进行，参数间耦合的研究较少。笔者以汽车片式悬臂型接触件为研究对象，建立接触件的力学模型与仿真模型，通过参数试验法研究弹片圆弧区半径、水平长度和宽度对接触件插拔性能的影响规律；采用最优拉丁超立方-响应面(optimal latin hypercube design response surface methodology，Opt LHD-RSM)联合的方法建立接触件多参数耦合模型，进行结构优化。

1 电连接器接触件模型

1.1 力学模型

针对某汽车片式悬臂型电连接器接触件，建立接触件力学模型。在接触件插合时由公端和母端弹片接触形成导通回路，并由弹片变形产生的弹力来保持接触件之间的接触。因此弹片的结构尤为重要。本文研究的接触件弹片分为圆弧上升区、圆弧过渡区以及倾斜下降区3个部分。接触过程中公端、母端受力如图1所示。

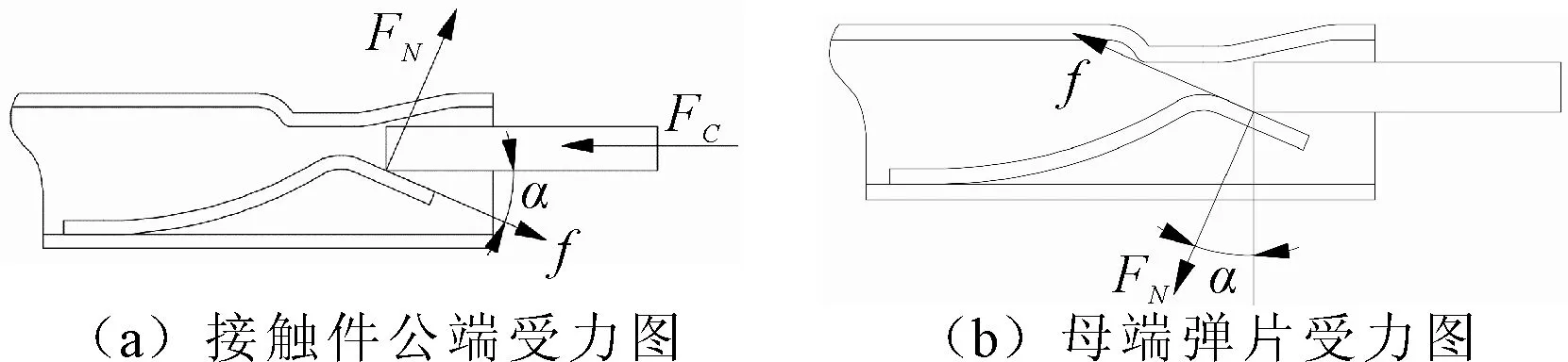
图1 接触件受力分析图

接触过程中公端、母端受力关系为：

(1)

式中：FC为公端受到的插入力；FN为母端弹片提供的支持力；f为公母端之间的摩擦力；F为母端弹片变形产生的弹力；α为弹片倾斜段的水平夹角。

在整个插合过程中，母端弹片因受力而变形，各区域的圆弧半径以及角度发生变化，其接触前后状态如图2所示。弹片产生的挠度ω为弹片倾斜段末端竖直方向的位移量，通过变形前后的几何分析，挠度与弹片倾斜角之间的关系：

Lx(sinα0-sinα)

(2)

式中：R1为接触前弹片前段圆弧的半径；β0为接触前弹片前段圆弧对应的角度；R2为接触前弹片后段圆弧的半径；α0为接触前弹片倾斜段的角度；Lx为弹片倾斜段的长度；α为接触件公端插入过程中弹片倾斜段的角度。

图2 接触件插拔示意图

将接触件母端弹片简化成悬臂梁结构，其所受压力与挠度之间的关系为：

(3)

式中：E为接触件的弹性模量；I为接触件母端弹片的截面惯性矩；c为弹片根部固定处到接触压力所作用点的长度；L为弹片根部固定处到弹片倾斜段末端的长度。

1.2 仿真模型

相较于力学模型，接触件仿真模型能更加直观地得出各部分的应力应变大小以及插拔循环产生的塑性变形积累。 笔者针对该汽车电连接器接触件进行ABAQUS插拔循环有限元仿真。

首先，建立电连接器接触件几何模型，由于模型精细化程度过高会导致计算时间过长、计算收敛困难等问题，模型略去接触件的压接部分。其次设置材料属性。该接触件材料为铜合金C19010，其性能参数如表1所示。设定边界条件，将接触件母端的后端面完全固定约束，在接触件公端的后端面顶部设置一个插入方向的位移来模拟插拔。最后整体采用四面体网格进行网格划分(近似全局尺寸设为0.02)，由于弹片起主要作用，采用更密的网格划分(近似全局尺寸设为0.01)，接触件模型如图3所示。

表1 接触件材料C19010性能参数及仿真参数

图3 接触件模型

1.3 模型准确性验证

为了验证仿真模型的准确性，对电连接器接触件进行插拔循环测试试验和仿真。考虑到连接器需要进行连接器厂的生产验证、线束厂的预装检验以及整车厂的装配，因此，在测试与仿真中进行5次插拔循环。

为避免偶然误差，挑选10个一致性较好的端子，在MTS 5 kN拉伸试验机进行测试，如图4所示。试验参照QC/T 1067.1-2017《汽车电线束和电气设备用连接器第1部分》进行，以50 mm/min匀速对插端子，然后以同样的速度分离，重复5次插拔，记录插拔力的变化值，其中，插到位所需的峰值力为插入力，稳定值为保持力。

图4 电连接器插拔循环测试图

按照上述测试条件进行接触件插拔循环仿真。设置10个分析步，每两个分析步代表一次插拔循环，得到5次循环过程中插拔力的变化值。

将仿真结果与10组样品试验结果的平均值进行比较，如图5所示。插拔循环仿真结果和试验结果在整体趋势上的变化是一致的。计算5次插拔循环中的插入力与保持力的最大相对误差均在10%以内，说明仿真模型准确度较好。此外，仿真结果与试验结果均表明，第一次插拔与多次插拔循环后的插入力变化较大。分析其原因可能是在插拔循环的交变应力作用下，接触件产生塑性积累，间隙增大，从而导致插入力减小。

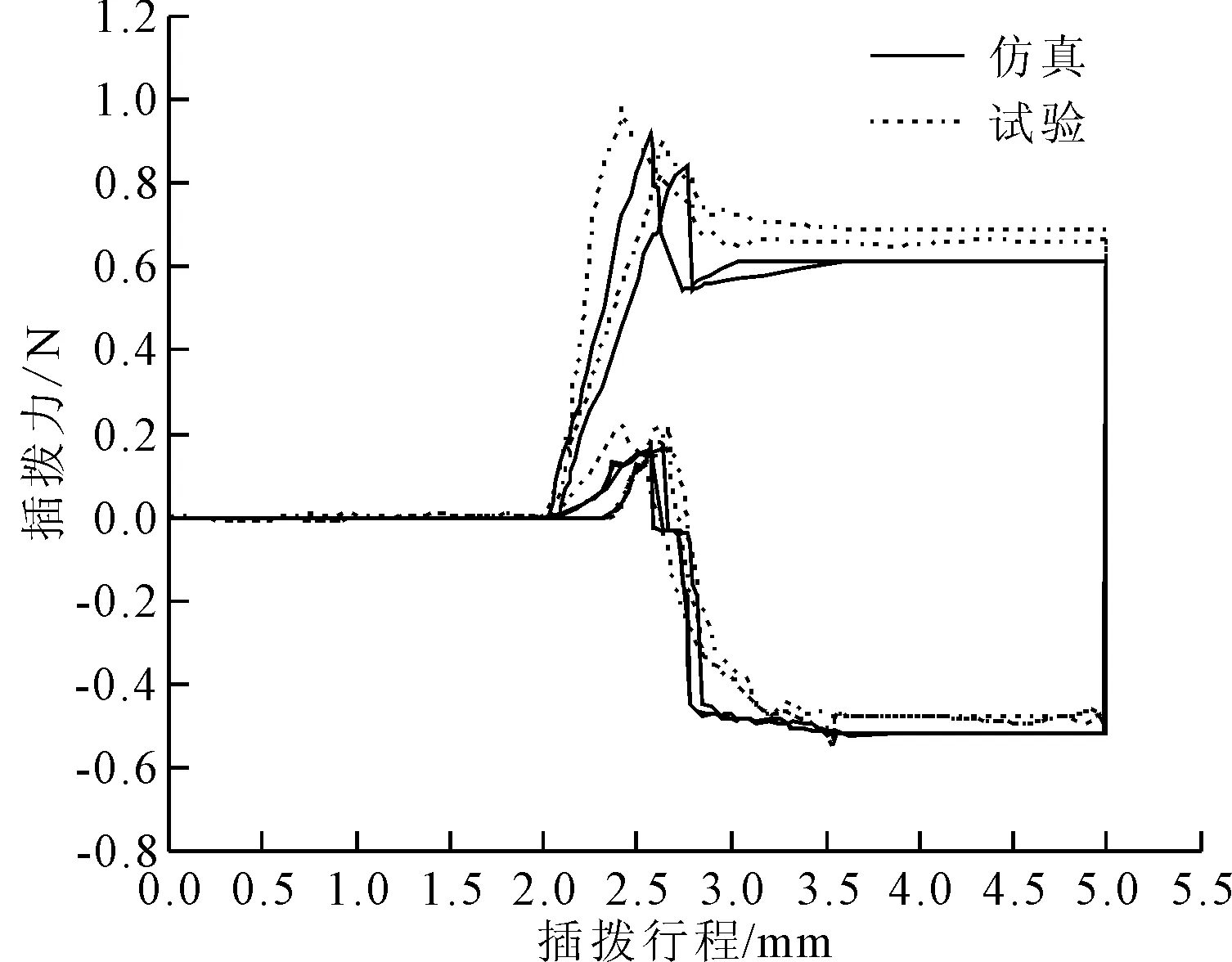
图5 插拔循环仿真结果与试验结果

2 接触件插拔性能单变量分析

由于弹片的结构参数(圆弧区半径R1、R2，弹片圆弧区水平长度L1、L2，弹片宽度b)对其插拔性能影响显著，为探究各参数对其插拔性能的影响规律，采用参数试验法(parameter study, PS)，设定3个样本组进行分析。由于R1与R2、L1与L2均为关联尺寸，b为独立尺寸，参数设定时，R1与R2、L1与L2需同倍率上下浮动，且需避免结构干涉问题。所设计样本参数如表2所示。

表2 设计样本点参数

2.1 弹片圆弧区半径对插拔性能的影响

在表2样本组Ⅰ的变化范围内，等间隔取9个样本参数，进行仿真求解，结果如图6所示。从图6可知，随弹片圆弧区半径的增大，接触件的插入力FC、保持力Fb、最大等效应力SMAX和间隙变化值Δh都会随之减小。两段圆弧区半径初始尺寸为5.97 mm和0.70 mm，当减小10%时，插入力增大22.75%，保持力增大15.33%，最大等效应力增大22.00%，间隙变化值增大446.81%；当增大10%时，插入力减小52.68%，保持力减小53.04%，最大等效应力减小19.17%，间隙变化值减小94.30%。可见弹片圆弧区半径对间隙变化值影响较大，较小的圆弧区半径会导致间隙变化值过大，从而导致接触松脱失效等问题。

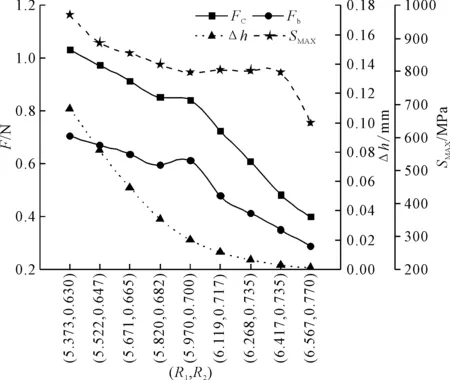
图6 弹片圆弧区半径(R1,R2)对插拔性能的影响

2.2 弹片圆弧区水平长度对插拔性能的影响

在表2样本组Ⅱ的变化范围内，等间隔取9个样本参数，进行仿真求解，结果如图7所示。从图7可知，随弹片圆弧区水平长度的增大，接触件的插入力FC、保持力Fb、最大等效应力SMAX和间隙变化值Δh都会随之增大。两段圆弧区水平长度初始尺寸为3.07 mm和0.36 mm，当减小10%时，插入力减小86.26%，保持力减小85.66%，最大等效应力减小69.68%，间隙变化值减小100.00%；当增大10%时，插入力增大29.82%，保持力增大4.39%，最大等效应力增大18.11%，间隙变化值增大733.80%。可见弹片圆弧区水平长度对间隙变化值影响较大，较大的圆弧区水平长度会导致间隙变化值过大，从而导致接触松脱失效等问题。

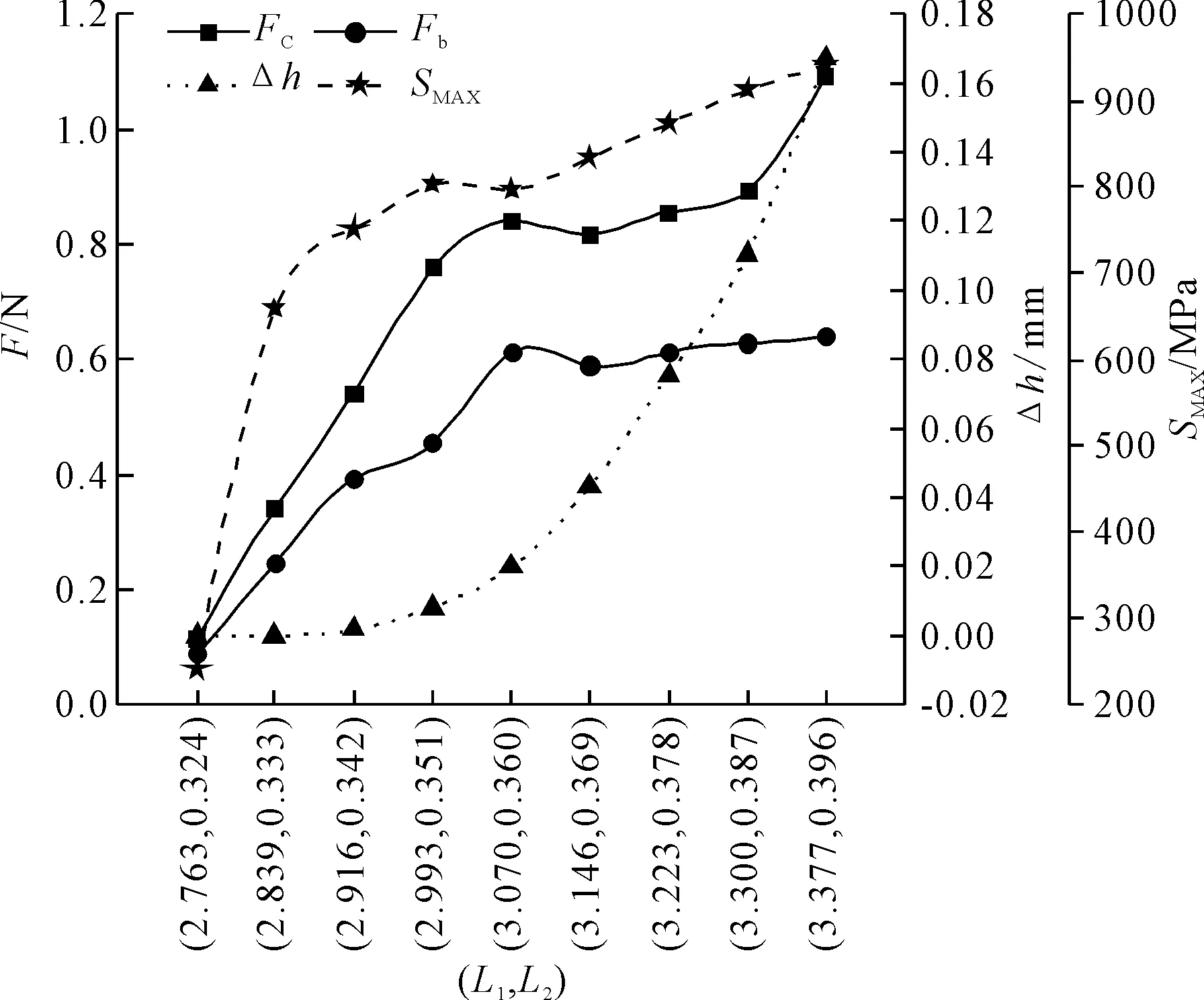
图7 弹片圆弧区水平长度(L1,L2)对插拔性能的影响

2.3 弹片宽度对插拔性能的影响

在表2变量组Ⅲ的变化范围内，等间隔取9个样本参数，进行仿真求解，结果如图8所示。从图8可知，随弹片宽度b的增加，插入力FC、保持力Fb和间隙变化值Δh都会随之增大，且趋于线性关系。弹片宽度初始尺寸为0.96 mm，当减小20%时，插入力减小18.61%，保持力减小18.63%，最大等效应力减小10.82%，间隙变化值减小17.87%；当增大20%时，插入力增大16.29%，保持力增大17.95%，最大等效应力增大12.09%，间隙变化值增大21.90%。最大等效应力SMAX随弹片宽度b的增加呈波动增长的趋势，其原因是因为宽度的增加，弹片的惯性矩增加，其接触压力升高，同时，宽度增加又导致其接触面积增加，使SMAX产生波动性变化，但其接触压力升高趋势更显著，因此具有略微上升趋势。

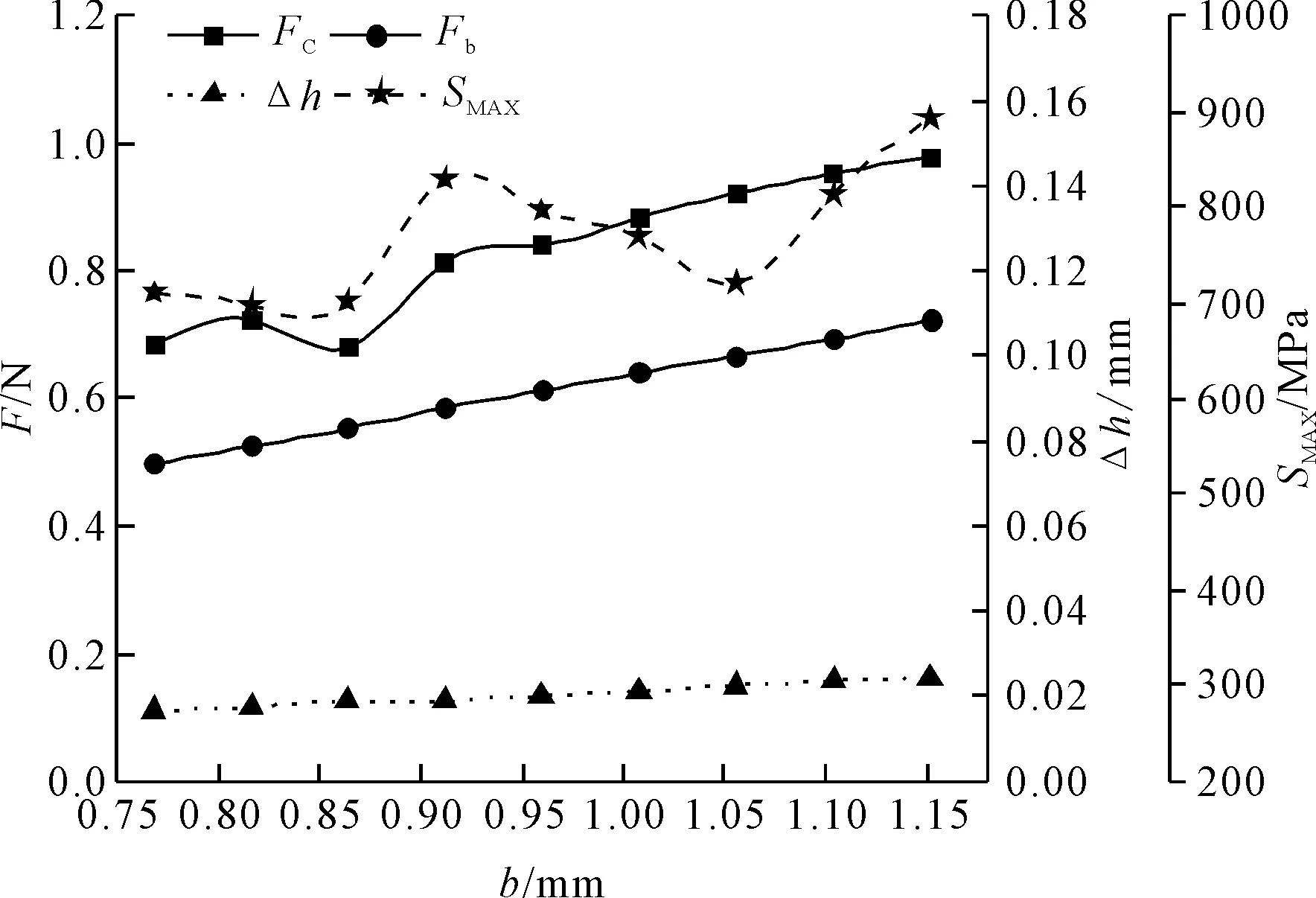
图8 弹片宽度b对插拔性能的影响

3 基于响应面模型的接触件插拔性能优化

应用单变量法分析得出弹片参数对插拔性能的影响规律，但是难以探究各参数间的耦合影响。为此，重新设计样本点进行仿真，建立接触件插拔性能响应面模型，对其结构进行优化。

3.1 最优拉丁超立方抽样

样本点的选取需均衡考虑拟合精度和计算成本。在满足模型拟合精度的要求下，尽可能使用较少的样本点。Opt LHD是一种分层采样方法，将所有变量都均匀选取相同数量水平，为某一变量随机选取各水平的值，并构建了相关系数矩阵Tij和相关系数ρmax，求取其他变量各水平的值，从而得到布满整个空间的样本点[10]。相比于蒙特卡洛、传统的拉丁超立方设计等采样方法，Opt LHD可以规避样本点集中现象，具有非常好的空间填充性和均衡性，且迭代次数较少。

采用Opt LHD在取样空间抽取40个样本点，其空间分布如图9所示。从图9可以看出样本点均匀性较好。通过仿真得到40个样本点的插拔性能，结果如表3所示。

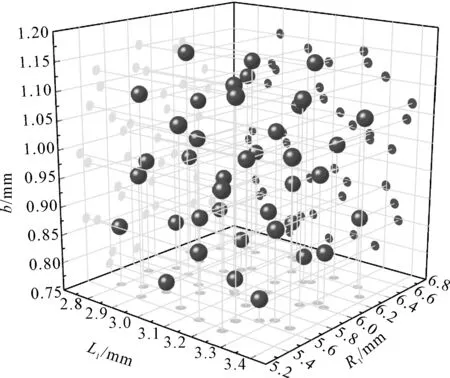
图9 Opt LHD样本点空间分布

表3 设计样本值与仿真结果

3.2 接触件响应面模型

响应面法(response surface methodology，RSM)可以建立多响应变量和多输入变量之间的数学模型。对于输入变量数目较少的问题，低阶响应面模型即可满足拟合精度[11]，高阶响应面模型精度提升相对较低，且计算量骤增，容易出现过拟合情况。因此，选用二阶响应面模型拟合接触件各参数对插拔性能的影响。

选取R1、L1和b为输入变量，接触件插入力FC、保持力Fb、最大等效应力SMAX、间隙变化值Δh为输出响应。二阶响应面方程为：

(4)

式中：xi、xj为输入变量；y是响应；β0为常数项；m为变量个数；ε为曲线方程误差；βi、βii、βij为系数，经多元线性回归确定。

基于PS抽样所建立的响应面近似模型(PS-RSM)如下：

(5)

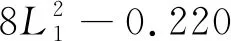
(6)

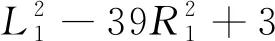
(7)

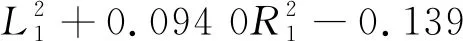
(8)

基于Opt LHD抽样所建立的响应面近似模型(Opt LHD-RSM)如下：

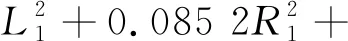
0.301 9b2+0.801 1L1R1+2.001 1L1b-0.439 6R1b

(9)

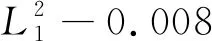
0.735 1b2+1.287 6L1R1+1.398 9L1b+0.149 4R1b

(10)

1 435.3b2+1 604.0L1R1+3 010.5L1b-1 034.2R1b

(11)

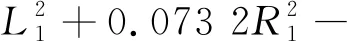
0.008 6b2-0.385 1L1R1-0.032 5L1b-0.015 8R1b

(12)

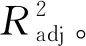
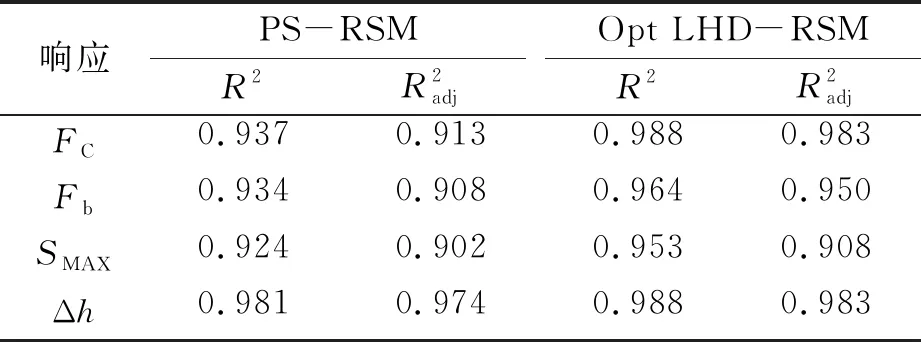
表4 响应面模型拟合可信度评估

对比两种响应面近似模型，发现各结构变量对响应的贡献程度不同。相比于PS-RSM模型，Opt LHD-RSM模型具有参数之间的相乘项，即考虑各参数之间的耦合，可以更准确地反映出接触件各参数对插拔性能的影响规律。

3.3 接触件参数优化及验证

接触件间隙变化值、插入力和最大等效应力越小，接触件越容易插入，但是会导致保持力过小，存在松脱风险。因此，需要综合考虑各性能指标。根据上述分析以最小间隙变化值Δh为目标，保证插入力FC在标准规定范围内，建立接触件优化模型：

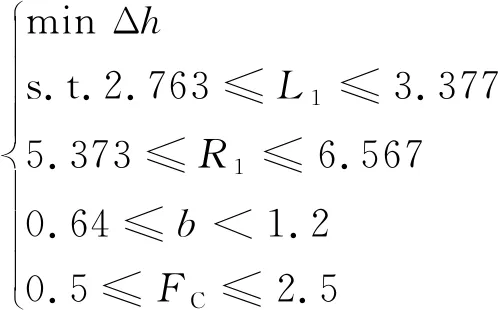
(13)

应用梯度优化法进行寻优。优化前后的接触件参数及插拔性能如表5所示。相比优化前，优化后接触件的间隙变化更小，降低182.2%，绝对值趋近于0，即5次插拔后接触件塑性变形量很小；插入力降低了34.38%，保持力降低了36.14%；最大等效应力降低了18.22%且符合标准规定的范围，保证了接触件具有一定的保持力，满足汽车连接器在多回路功能模块中的应用时不发生松脱。

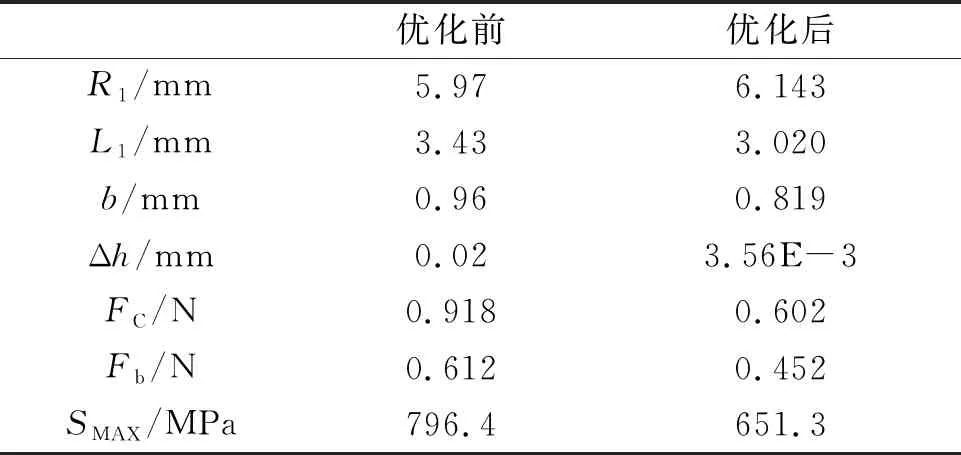
表5 优化前后接触件性能比较

为验证优化结果的可靠性，使用优化后的结构参数进行建模和仿真。比较优化结果和仿真结果，如表6所示。各插拔性能指标误差均小于±5%，优化结果可靠。

表6 优化结果与仿真结果比较

4 结论

(1)接触件多次插拔产生塑性累积应变，回弹量减小。仿真结果表明，5次插拔后，接触件插拔性能下降显著。在汽车连接器设计时，必须考虑多方预装检测导致多次插拔所带来的影响。

(2)通过研究接触件结构参数对插拔性能的影响规律，发现接触件弹片圆弧区半径和水平长度对间隙变化值影响较大，弹片宽度与插入力、保持力和间隙变化值趋近于线性关系。

(3)基于Opt LHD-RSM建立接触件弹片多参数耦合模型，优化其结构。优化后，接触件间隙变化值降低82.20%，插入力降低34.38%，塑性变形量减小，具有更好的插拔性能。