基于不连续脉宽调制永磁同步电机边带声振响应数值预测

张黎明，邱子桢，陈 勇，成海全，武一民，张志金

(1.河北工业大学 天津市新能源汽车动力传动与安全技术重点实验室，天津 300130；2.艾迪捷信息科技（上海）有限公司，上海 200120）

当前，作为电驱动系统的关键部件，永磁同步电机因其宽调速范围、高能量密度和高可靠性等优点，在电动汽车领域得到了广泛的应用。电驱动系统的噪声、振动与声振粗糙度(Noise，Vibration &Harshness，NVH)对于整车系统的性能开发至关重要。与传统内燃机汽车相比，由于缺少了发动机的掩蔽效应，永磁同步电机驱动系统所辐射的高频声振响应更为显著[1]，逐渐成为整车与部件级NVH 性能开发与优化的研究热点。

永磁同步电机逆变驱动系统通常采用空间矢量脉宽调制(Space Vector Pulse-width Modulation，SVPWM)策略，以实现较高的直流母线电压利用率[2]。然而，由SVPWM所引入的高频边带电流谐波主要集中在载波频率及其整数倍频附近，不仅对电驱动系统的声振特性造成严重影响，而且还会辐射出刺耳的高频电磁噪声[3]。因此，在电驱动控制系统设计开发阶段，对边带谐波成分进行快速、准确分析尤为重要，并且对边带声振响应抑制优化大有裨益。

为了研究边带电流谐波对电磁力的影响规律，文献[4]对PWM(Pulse Width Modulation，PWM)所引入的电流谐波特性进行了分析，并推导了相应的径向电磁力解析模型。文献[5-7]通过建立永磁同步电机边带谐波分量解析模型，揭示了径向电磁力的时空分布规律。文献[8]对比分析了SVPWM 内、外转子永磁同步电机的边带电磁力频谱分布，分析了不同极槽配合对边带电磁力的影响，为永磁同步电机的噪声识别与优化提供了理论基础。

为了研究脉宽调制技术对电机声振响应的影响，文献[9]研究了由逆变器驱动的感应电机电磁激励与电磁辐射噪声之间的关系，并对电流谐波与声振响应进行了频谱分析，结果表明电磁激励与辐射电磁噪声具有强相关性。文献[10]研究了在线与离线脉宽调制技术的基本特征及其对电机电磁噪声的影响，并通过变速工况实验验证了理论解析的准确性。文献[11]采用联合仿真的分析方法，研究了宽调速范围内，逆变器电流谐波对弱磁调速与恒转矩调速电机振动噪声的影响，结合仿真结果与实测数据得出逆变器供电永磁同步电机的振动噪声频谱增量主要体现在载波频率附近。文献[12]分析了不同载波频域的边带电流谐波与机械振动噪声之间的关系，为永磁同步电机的声振预测提供了理论依据。

上述有关电流谐波及声振响应的研究均基于连续脉宽调制(Continuous Pulse-width Modulation，CPWM) 策略[13－14]，对于不连续脉宽调制(Discontinuous Pulse-width Modulation，DPWM)策略产生的边带谐波特征规律研究尚不完善。DPWM能够显著提高逆变效率，已经广泛应用于高功率型电压源逆变器中[15－16]，然而其产生的边带谐波成分更加丰富。为此，本文以一台12 槽-10 极永磁同步电机为研究对象，对DPWM策略所引起的边带电流谐波及声振响应进行了特征识别与分析，基于DPWM的空间矢量原理与实现方法，建立了“机-电-磁-控”多物理场协同仿真模型，通过Simulink &JMAG 仿真预测了DPWM 策略对边带电磁力以及高频振动噪声的影响，分析了边带电流谐波及径向电磁力的频谱特征，并基于模态叠加与完全积分法计算了实验样机的声振响应。最后，通过搭建12槽-10极永磁同步样机边带电流谐波与声振响应实验，对边带成分的频谱特征进行分析，验证了理论解析与协同仿真模型的准确性。

1 DPWM原理与实现方法

1.1 DPWM基本原理

作为典型的CPWM 策略，SVPWM 的工作原理是根据U所在扇区的空间位置，确定要输出的基本空间电压矢量[17]。图1 为SVPWM 的电压空间矢量扇区图，以第一扇区为例，SVPWM的开关序列如图2(a)所示。在一个载波周期内，SVPWM将有效空间矢量居中放置，两个零矢量边沿对称放置，逆变器各相桥臂根据载波频率不断地进行开关切换。

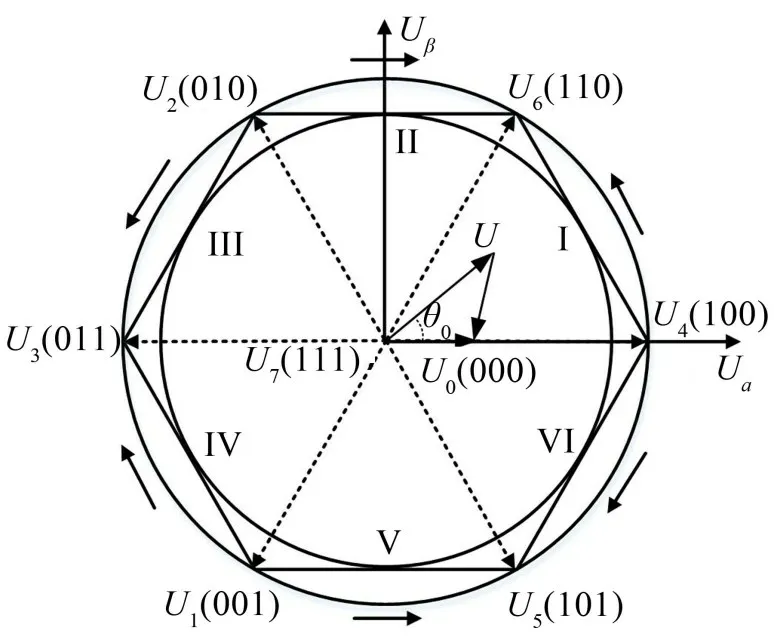
图1 电压空间矢量扇区图

由CPWM 转化为DPWM 最为直接的方式是将相邻半个载波周期内的有效空间矢量彼此相连，通过摒弃一个零矢量使得A 相桥臂被钳位在特定状态[18]，如图2(b)所示。通过不同的钳位方式，可以得到6 种典型的DPWM 方案，即DPWMMIN、DPWMMAX、DPWM0、DPWM1、DPWM2 和DPWM3。

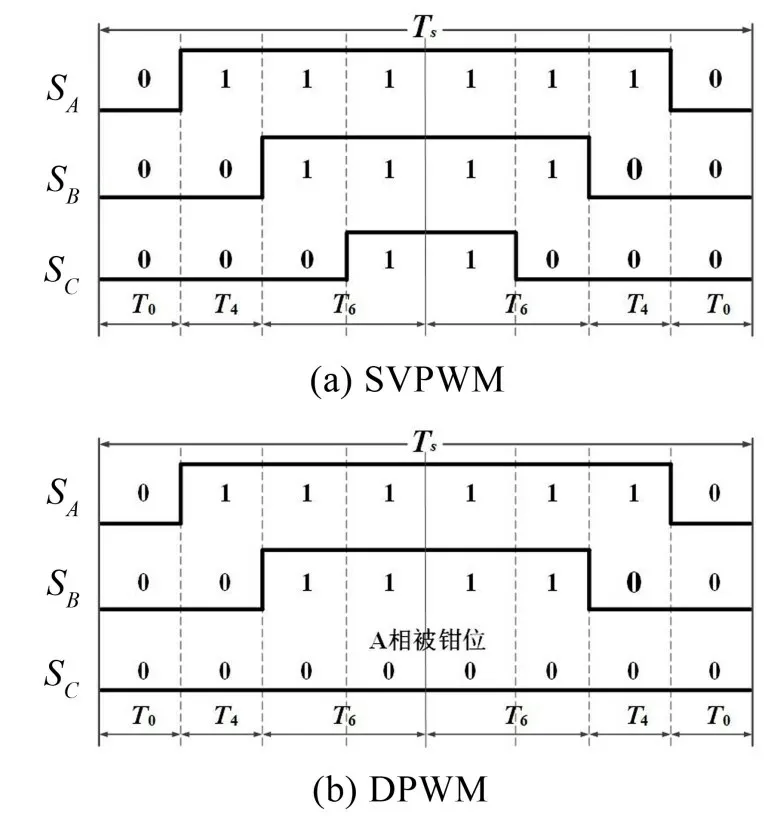
图2 开关序列图

1.2 DPWM实现方法

DPWM 的实现方式与SVPWM 类似，本质上都是通过对正弦调制波注入共模电压信号的方式来实现，其共模电压Uz计算公式为：

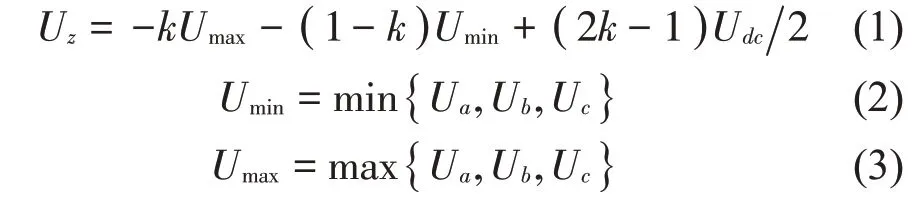
式中：Ua、Ub、Uc分别为三相相电压；Umax、Umin分别为最大和最小输出电压；k为零矢量分配因子，取值为0或1，具体取值如表1所示。

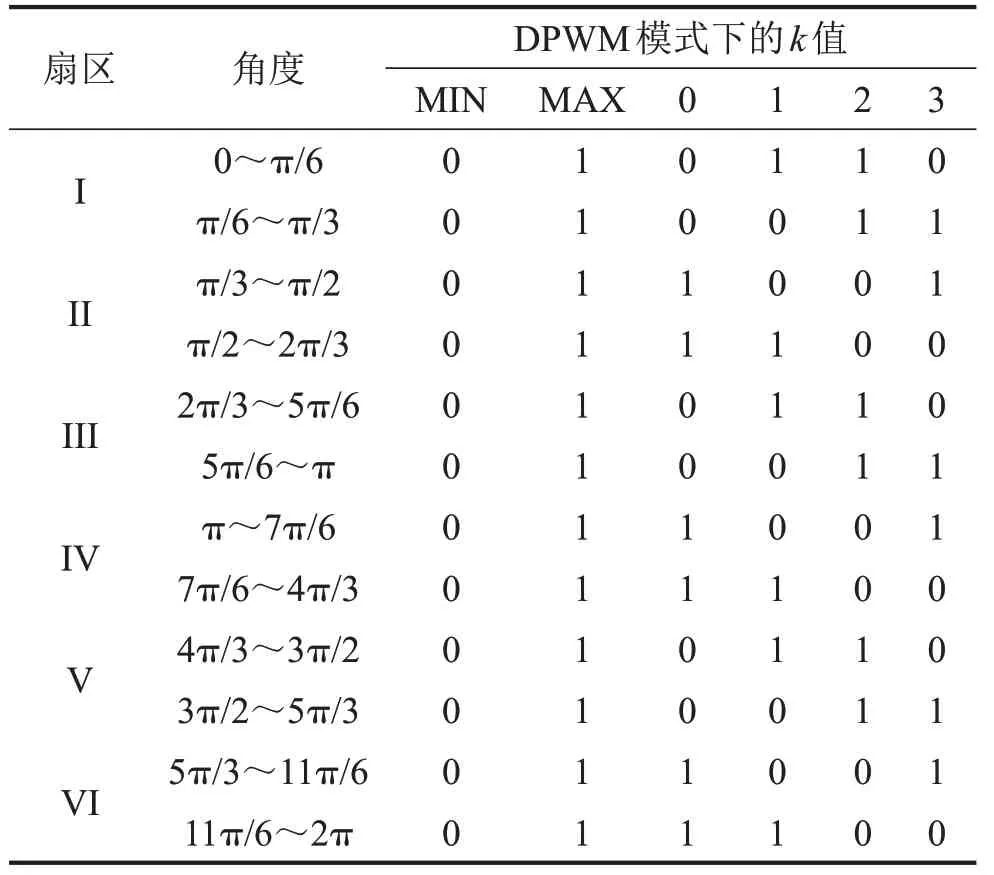
表1 不同DPWM模式下k的取值

(1)DPWMMIN和DPWMMAX

当整个开关周期满足k值恒取1或0时，即仅有一个零矢量U7(1 1 1)或U0(0 0 0)与相邻矢量进行组合，对应DPWMMIN和DPWMMAX模式，相应调制波波形如图3所示。各相桥臂依次被钳位到最大值或最小值，谐波性能较差。

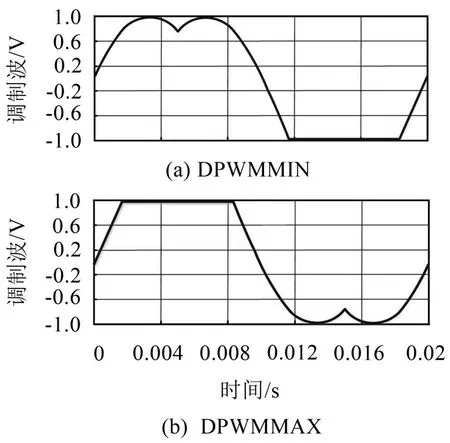
图3 DPWMMIN与DPWMMAX调制波波形

(2)DPWM0和DPWM2

当k在第一、三、五扇区值取为0，第二、四、六扇区值取为1 时，对应DPWM0 模式，调制信号在钳位区间内超前π/6输出电压峰值；反之则为DPWM2模式，相应调制波波形如图4 所示。相比于DPWMMIN/MAX 策略，该类型下的调制波波形趋于对称，谐波性能有所改善。

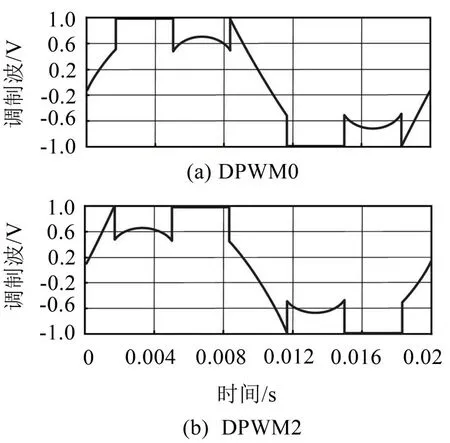
图4 DPWM0与DPWM2调制波波形

(3)DPWM1和DPWM3

将原始的6 个扇区对称划分成12 个扇区，各扇区零矢量U7(111)或U0(000)交替进行工作，将k的取值在每个扇区内分别赋予0 和1 两个值，即可获得DPWM1和DPWM3模式，相应调制波波形如图5所示。相比于其他类型DPWM，该类型下的调制波波形呈现对称性，谐波性能最优。

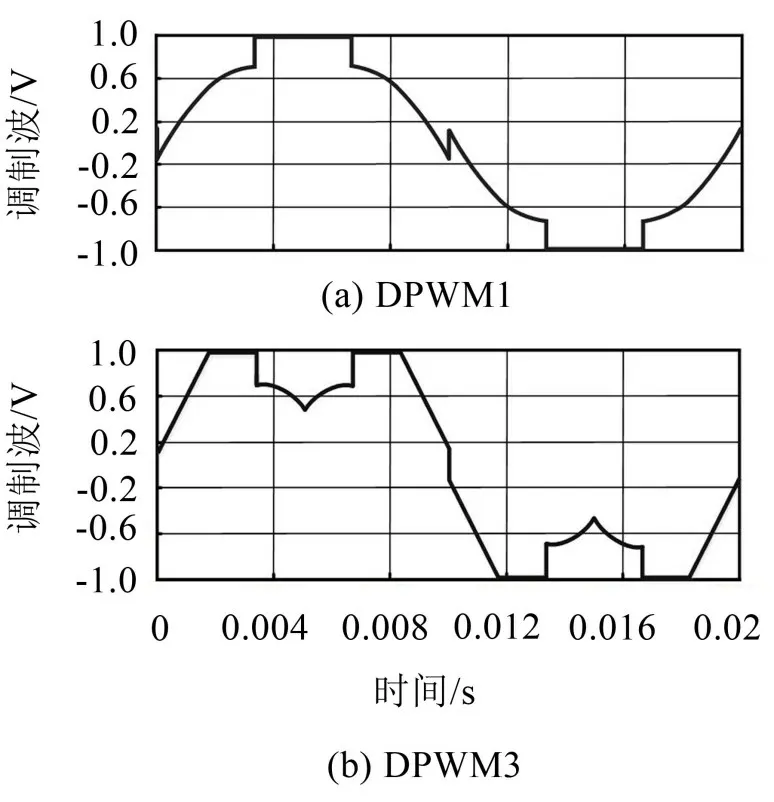
图5 DPWM1与DPWM3调制波波形

2 边带电磁成分特征解析

2.1 径向电磁力分析

在径向磁通永磁同步电机中，作用在定子上的径向电磁力是引起电机振动的主要因素。电磁力密度可由麦克斯韦应力张量法定义：

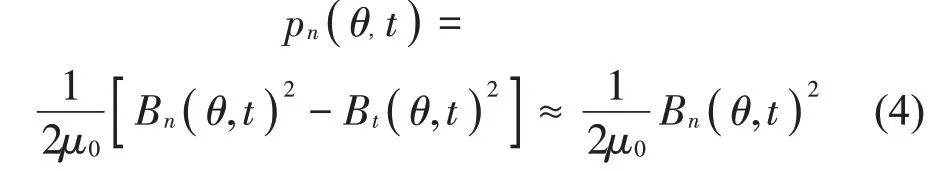
式中：Bn为径向气隙磁密，Bt为切向气隙磁密；μ0为真空磁导率；由于Bn远大于Bt，因此，忽略了切向气隙磁密所产生的电磁力影响。

由于基波电枢场与谐波电枢场的幅值较小，为简化计算，仅考虑永磁体磁场与谐波电枢场相互作用产生的边带电磁力[12]。因此，边带径向电磁力密度可以表示为：

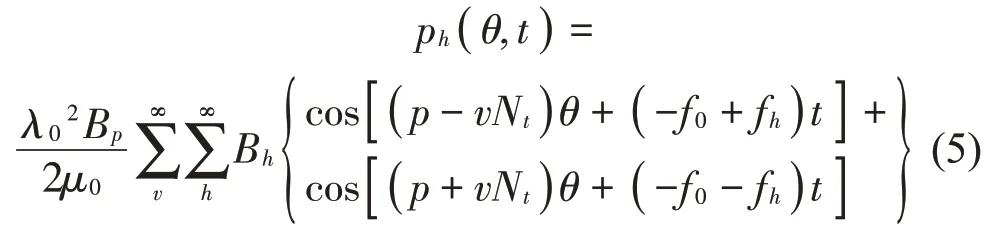
式中：Bp和Bh分别为永磁场磁密和谐波电枢场磁密。可以看出边带电磁力具有明显的空间阶次p±vNt和频率次数f0±fh，其共同决定了边带谐波分量的分布特征。为进一步解析载波频率附近的边带电磁力，还需对边带电流谐波进行分析。

2.2 考虑电流谐波的边带电磁力特征

DPWM 中的载波频率可以表示为fc，调制波频率可以表示为f0。边带电流谐波的解析表达式可以从转子和定子坐标系中推导得出[5]。主要边带谐波的频率分布可以表示为nfc±kf0，其中n和k由不同的奇偶校验组成。以第一载波频域为例，n为1。忽略幅值较小的高次谐波，DPWM中的边带电流谐波可以表示为：

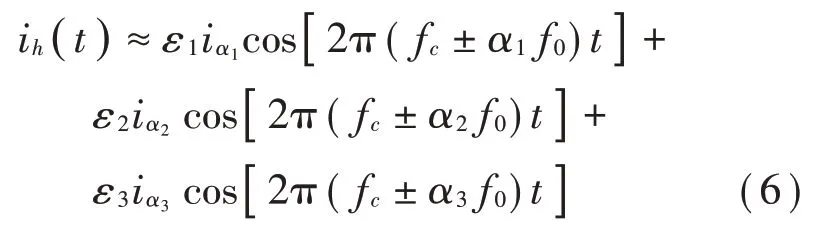
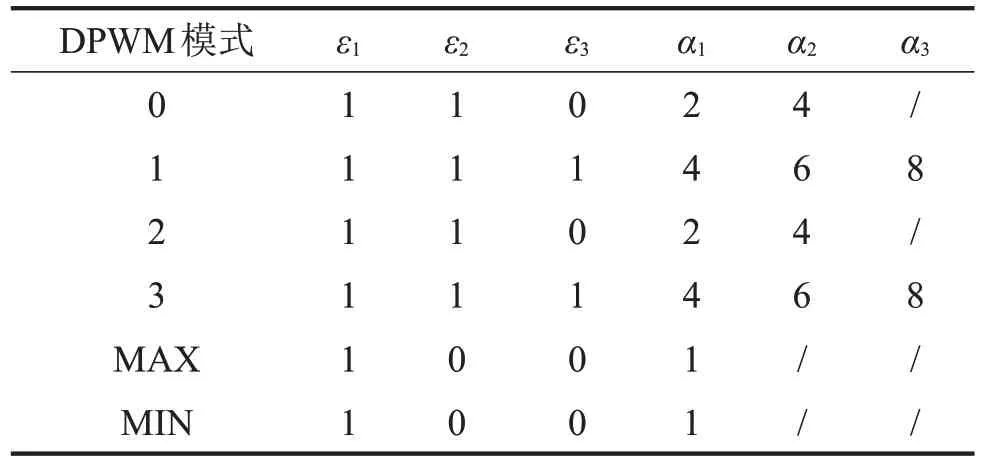
表2 不同DPWM模式对应的ε1、ε2、ε3、α1、α2、α3

边带电流谐波的幅值大小取决于电机的调制比与转速[6]。不同DPWM模式下的电流谐波分布可根据式(6)与表2得出。

为分析边带电流谐波引起的电磁力，可将边带电流谐波分量转化为对应特征频率的磁通分量，通过计算得出边带电磁力。以特征频率为fh=fc+2f0的电流谐波分量为例，其引起的边带电磁力特征频率可表示为：

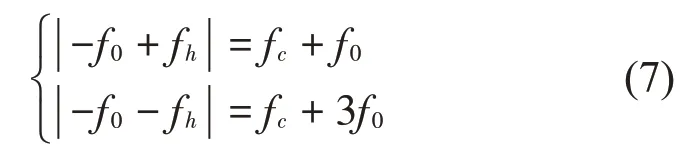
载波频域附近边带电磁力的频率分布如表3所示[19]。由此可进一步地对永磁同步电机声振响应进行分析与识别。

表3 DPWM边带谐波分量频率分析

3 电磁振动响应预测与验证

3.1 边带电流谐波分量

本文以一台12 槽10 极永磁同步电机为研究对象，分析了6种DPWM策略下电机的高频声振响应，电机主要参数如表4所示。

表4 永磁同步电机的主要参数

由于测试样机的工作环境为500 r/min～1 500 r/min 和2 N∙m～6 N∙m，故选择1 000 r/min 和4 N∙m作为稳定工况，对6种DPWM的边带成分进行特征频率识别与分析。图6为1 000 r/min和4 N∙m工况下6 种DPWM 策略的仿真与实测电流频谱，载波频率fc=8 000 Hz，电流基频f0=83.33 Hz。为验证电磁分析模型的准确性，对DPWM控制下的电机模型进行了仿真分析，并参照实验数据对模型进行修正。从图中可以看出，仿真结果相对实测数据幅值略低，但频率特征基本吻合且与上述理论分析一致，验证了电磁解析模型的准确性。

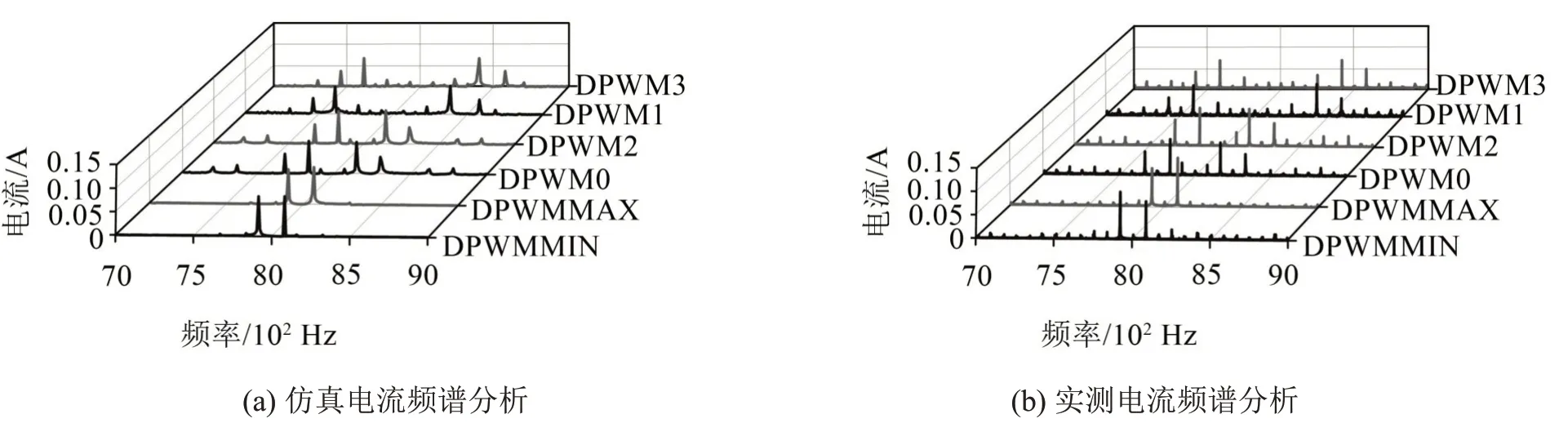
图6 DPWM边带电流谐波频谱分析

同一类型、不同模式的DPWM具有相似的频率特征。DPWMMIN与DPWMMAX主要边带分量集中在中心频率fc附近，位于fc±f0处。对于DPWM0与DPWM2，主要边带分量对应的特征频率为fc±2f0和fc±4f0。DPWM1 与DPWM3 的主要边带分量距中心频率fc较远，位于fc±5f0和fc±7f0处。

3.2 边带电磁力有限元分析

通过有限元计算，可以得出1 000 r/min 和4 N∙m工况下电机的径向电磁力密度。分解得到边带电磁力频谱如图7 所示。图7(a)为电机在DPWMMIN与DPWMMAX策略下的边带电磁力频谱，从图中可以看出，边带电磁力主要集中在中心频率fc与fc±2f0。对于图7(b)中的DPWM0与DPWM2，其主要边带成分特征频率为fc±f0、fc±3f0和fc±5f0。图7(c)中DPWM1与DPWM3主要边带成分位于fc±4f0、fc±6f0和fc±8f0。图7 中所示的边带电磁力特征频率与表3 中的结论相符，验证了边带电磁力理论分析的准确性。

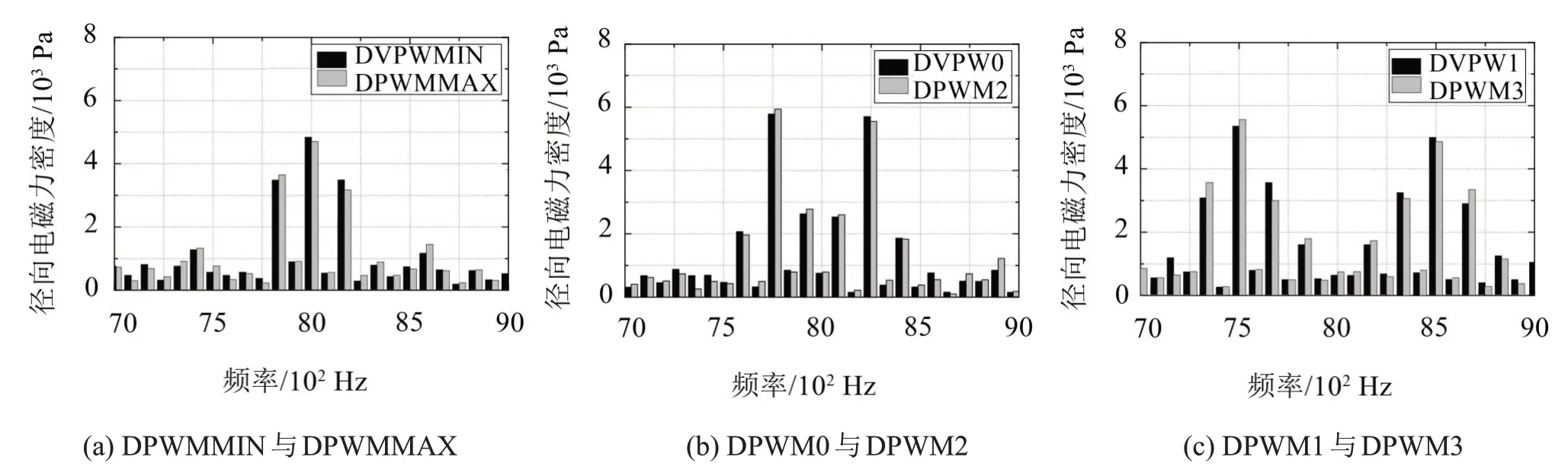
图7 边带电磁力频谱分析

3.3 模态分析

在JMAG-Designer中进行有限元分析以获取样机的模态参数。由于电磁力沿轴向几乎均匀分布，因此周向模态对振动的贡献量最大。为验证有限元模型的准确性，本文采用移动力锤法进行了模态实验。实验过程中，采用弹力绳将样机进行悬挂，同时放置了5个加速度传感器以获取壳体表面的振动响应。表5 列出了实测与仿真的模态振型及频率，并将仿真结果中的前端盖隐藏，以此来更加直观地体现各阶振型。结果表明，实测与仿真相对误差均在5%以内，表明了有限元模型的准确性。

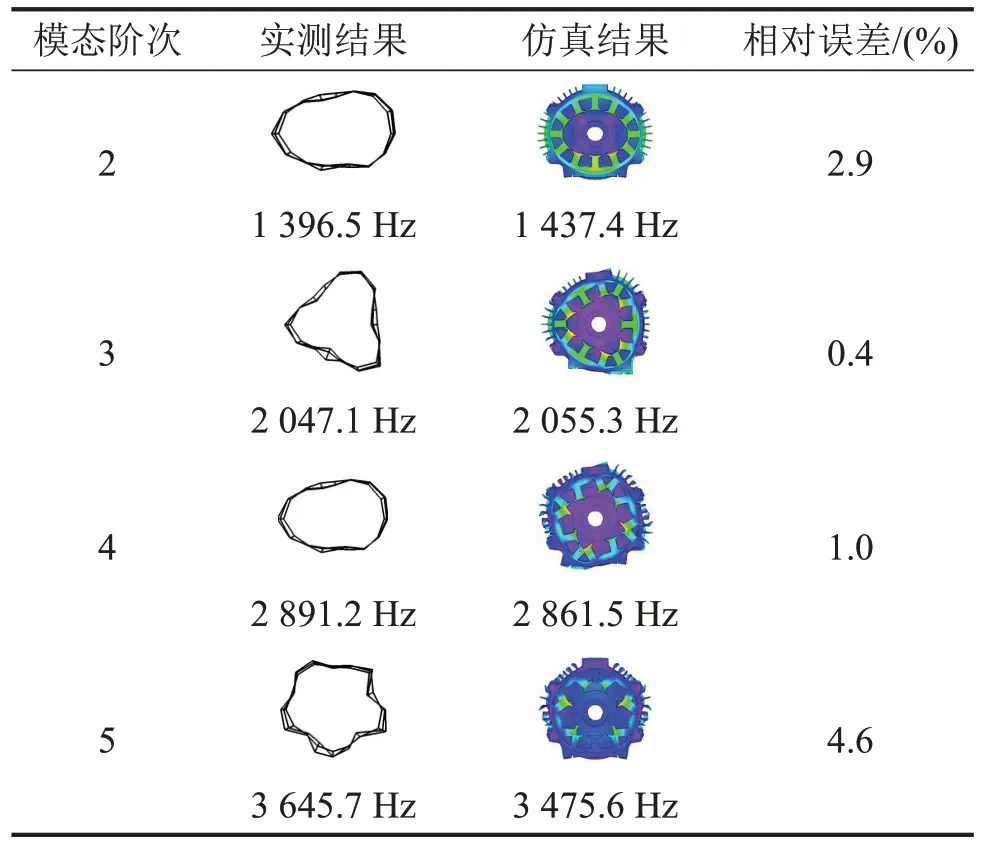
表5 模态参数实验验证

电机的结构特性对其振动噪声影响较大，当电磁力频率与固有频率接近时会引起共振，进而恶化电机的振动噪声[20]。本文主要分析高频部分，即载波频率附近的边带分量。结合图7 可知，边带电磁力的频率在8 000 Hz 附近，与结构的前5 阶固有频率相差较大，因此不易产生共振现象。

3.4 振动响应

为计算样机的振动噪声响应结果，建立了多物理场仿真模型，计算流程如图8所示。首先，基于二维电磁模型得到作用在定子齿表面的节点力，并将节点力映射到结构模型中作为激励，最后通过模态叠加法计算样机的振动响应。

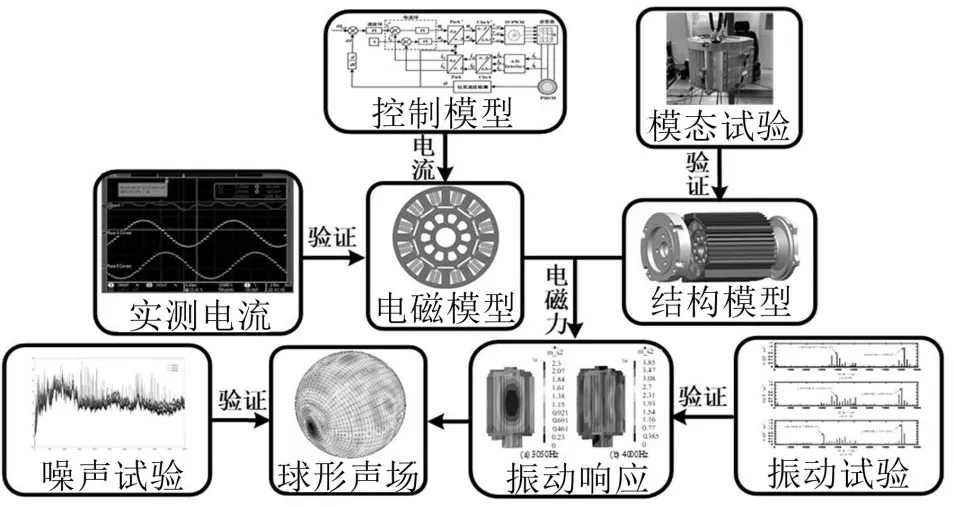
图8 电机振动噪声分析流程

模态叠加法的公式可表示为[21]：

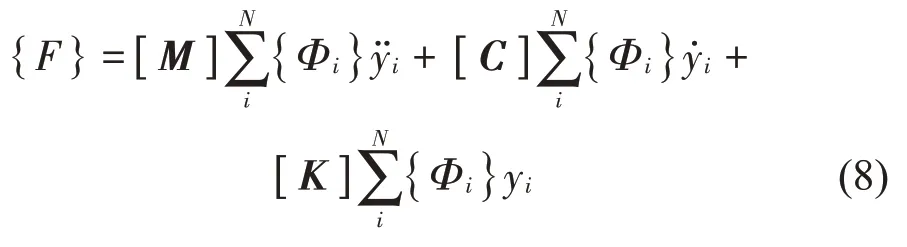
式中：[M]、[C]和[K]分别为质量、阻尼和刚度矩阵；N为叠加的模态阶次；Фi为第i阶模态振型；yi为节点模态坐标系中的位移。

为验证计算结果的准确性，本文进行了实验验证，振动噪声实验台架如图9所示。

图9 电机振动噪声实验台

基于dSPACE 半实物仿真系统，利用Simulink和电机控制器来实现PWM 信号发波及调制策略的实时切换。图10 为6 种DPWM 模式下样机的振动加速度频谱，可以看出,边带特征频率较为明显，仿真结果与实测数据基本吻合。DPWMMIN 与DPWMMAX 的振动峰值频率为fc，由于该类型DPWM的边带电流谐波幅值较大，导致电机的振动特性有所恶化。对于DPWM0与DPWM2，其峰值频率为fc±3f0，相比于DPWMMIN与DPWMMAX，该类型DPWM的振动特性有所改善。DPWM1与DPWM3的边带振动加速度峰值位于fc±6f0，相比于其他DPWM类型，其振动加速度幅值最低。结合边带电磁力频谱可知，边带振动分量与边带电磁力的频率特征基本一致，表明边带电磁力是产生电机高频边带振动的主要原因。

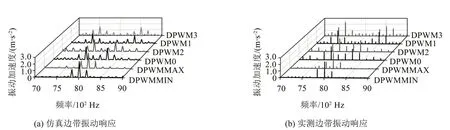
图10 1 000 r/min和4 N·m工况下DPWM边带振动响应分析

4 电磁噪声预测与验证

基于前文振动响应分析结果，预测了6 种DPWM 策略下的样机噪声。为更好地反映人耳对实验中所测噪声的真实感受，采用A 计权dB(A)法对实验所得声学结果进行处理。图11 所示为1 000 r/min和4 N∙m工况下，样机高频边带噪声A计权声压级的仿真结果与实测数据对比。可以看出，由边带电磁力所引起的高频电磁噪声具有明显的频率特征。DPWMMIN与DPWMMAX的边带噪声峰值为59.2 dB，对应特征频率为fc，其边带噪声幅值是6 种DPWM 中最高的。相比于DPWMMIN 与DPWMMAX，DPWM0 与DPWM2 的噪声特性有所改善，其边带噪声峰值为57.5 dB，对应特征频率为fc-3f0。DPWM1 与DPWM3 的边带噪声幅值最低，其值为56.1 dB，对应特征频率为fc-6f0。可以看出，这些边带噪声分量都是由边带电流谐波所引起的，验证了用于电磁噪声计算的多物理场协同仿真模型的准确性。由于仿真计算只考虑电磁力对振动噪声的影响，忽略了实验台架装配误差及控制器谐波丰富等非理想因素，进而导致部分频率的仿真结果略低于实验值。

图11 1 000 r/min和4 N·m工况下DPWM边带噪声响应分析

5 结语

本文研究了基于DPWM 策略的永磁同步电机边带振动声学特性，分析了边带电流谐波与径向电磁力之间的关系；建立了“机-电-磁-控”协同仿真预测模型，对6 种DPWM 策略边带声振响应的频谱分布与幅值特征进行了数值预测。通过12槽-10极的永磁同步样机稳态工况实验，验证了理论分析和协同仿真预测模型的准确性，得出结论如下：

（1）基于多物理场构建的协同仿真模型能够准确预测各DPWM方案的边带声振响应；通过模态试验获取了结构本身的固有特性并对有限元模型进行修正，实测与仿真振型及频率误差均在5%以内。

（2）6 种DPWM 策略中，DPWMMIN 与DPWMMAX策略的边带声振响应幅值最高，峰值集中在中心频率fc处；DPWM0与DPWM2策略的声振响应幅值相对DPWMMIN 与DPWMMAX 较低，峰值位于fc±3f0；DPWM1 与DPWM3 策略的声振响应幅值最低，峰值位于fc±6f0。

（3）本文所提出的分析方法可适用于多种PWM策略下永磁同步电机的边带声振预测分析，可为永磁同步电机的边带声振特征识别与优化提供新思路。