基于极点配置法的电磁分流阻尼优化设计
2022-12-20毛崎波
李 戈,毛崎波,王 永,谢 冉
(1.南昌航空大学 飞行器工程学院,南昌 330063;2.国网上海市电力公司特高压换流站分公司,上海 201413)
将电磁分流阻尼(Electromagnetic Shunt Damper,EMSD)用于结构振动控制是一种新发展的被动控制方法,其优点包括能产生较大控制力以及阻尼力,信号具有很宽的频率响应范围,传递力为非接触式等。EMSD的原理是利用线圈与永磁体的相对运动产生的电磁阻尼力[1]来降低系统的振动强度,并通过外接的分流电路消耗或者收集由系统的机械能转化而来的电能[2]。根据机电类比,当把LRC等2阶串并联电路作为EMSD 的分流电路时,可以将EMSD 视作一个附加在主系统上的调谐质量阻尼器[3],因此EMSD 等效于一个刚度、质量以及阻尼可以被方便地调节的调谐质量阻尼器,而对于参数可调的EMSD 来说,关键是要求解出分流电路的最优设计参数。Cheng 等[4]表明将EMSD 用于结构振动控制时,电磁耦合系数(即电磁系数)越大(线圈电感为预设值,因此电磁系数越大机电耦合系数也越大),控制效果越好。这种现象在Zhu 等[5]的论文中得到了详细的证明,即电磁系数越大,虚拟质量越大,就是质量比越大,EMSD 的控制效果越好。而目前在基于EMSD 分流电路优化设计的常见方法,比如定点理论(即H∞优化[6])和H2优化等(见Inoue 等[7]以及Tang等[8]文献),所得到的最优调谐比的解析表达式中,机电耦合系数的取值范围均被限制为0~2,而通过分析文献[3]的结论可知:利用H2优化考虑主系统阻尼时EMSD分流电路的设计参数,基于LRC串联分流的EMSD 的机电耦合系数将会小于0~2 中的某个数。比如当主系统的阻尼比为0.05 时,机电耦合系数被限制在1.709 9之内,而且主系统阻尼比越大,机电耦合系数被限制得越小。而实际上,对于文献[3,7-8]中的最优调谐比来说,当机电耦合系数接近1.709 9 或者2 时,最优调谐比将会趋近于0,此时按照这种最优设计所得分流电路的最优电容将变得非常大,从而很难实现最优控制。因此,传统的定点理论以及H2优化方法显然并不适用于机电耦合系数取较大数值时的EMSD的优化设计。
极点配置法是通过优化配置闭环系统的极点在复平面上的位置,使得系统的衰减系数最大化,是使得系统的暂态分量衰减最快的一种优化方法。国内的柳维玮等[9]针对压电分流阻尼电路提出了极点配置方法,她的研究表明运用极点配置方法设计的压电分流电路有着良好的抑制振动的效果。Belotti等[10]提出了一种称为“区域极点配置”的方法控制线性系统的振动,并验证了该方法的有效性。国外的Olanipekun 等[11]使用极点配置法改变了以平动模态为主的低频模态的极点位置,避免了行星齿轮系的共振。
由于不论研究对象是多少个自由度的系统,其响应一般是通过模态叠加法求得的,关键部分仍然还是单自由度系统的计算过程。因此本文针对机电耦合系数大于等于2 的情况,在采用EMSD 控制单自由度系统或者结构的单模态振动时引用定点理论和H2优化,对于基于EMSD的分流电路最优设计失效的问题,提出使用经典的极点配置法,解决在机电耦合系数大于2时基于EMSD分流电路的最优化设计问题。

1 机电耦合模型
如图1所示,R0为线圈电阻,R1为线圈外接的分流电路电阻;L0为线圈电感,电感值为固定值;为感应电动势[12-13],其中ϕ为电磁耦合系数(又称电磁系数),与线圈的匝数N、永磁铁磁场强度B、线圈长度l有关。k为主系统的刚度,m为主系统的质量,c为阻尼系数,主系统的阻尼比ζ0=c/(2mω0);图1中,电磁阻尼力fem=ϕI[13],与主系统受到的惯性力方向相反。假设R为分流电路等效电阻,则图1所示的机电耦合方程可表示为[14]:

图1 将参数可调的电磁分流阻尼用于单自由度振动控制模型
不考虑式(1)中的线圈电磁系数ϕ损耗,则机电耦合系数可以表示为ψ=ϕ2/(Lk)。再假设ω0=,分流电路振荡频率为ωd=,分流电路调谐比为,分流电路的频率比为,阻尼比为。文献[14]中推导了将EMSD用于有阻尼单自由度系统振动控制时的位移放大因子的无量纲表达式,如式(2)所示:

2 极点配置方法设计
在极点配置法中要考察系统衰减系数最大化的效果,因此首先要得到系统的传递函数,然后由传递函数得到极点特征方程,再按照实际需要来配置主导极点在复平面上的位置,使得主导极点距离虚轴最远,从而使系统的暂态分量衰减最快。考虑将系统的位移X作为输出量,激励力F为输入量,由式(1)可得传递函数如式(3)所示:

式中:s=σ+jω,令式(3)的分母为0,等式两边同时除以Lm可得极点特征方程,如式(4)所示:
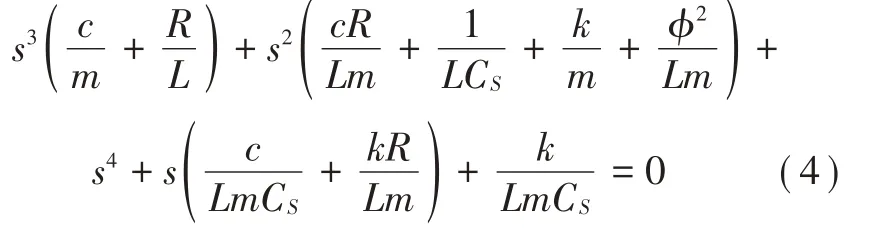
含有无量纲参数的式(4)表达式如式(5)所示:
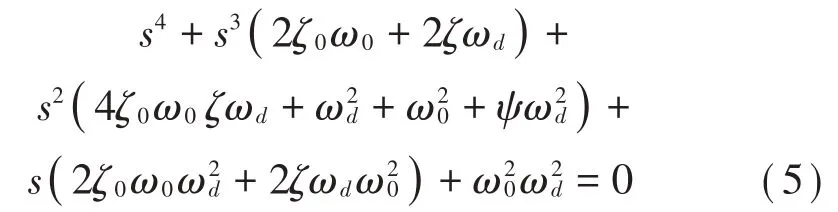
对暂态分量的衰减起主导作用的是离虚轴最近的极点。为此配置以上两对极点在复平面上重合,令A1=A2=A,B1=B2=B,则有:

因此将式(4)和式(5)表示为如式(6)所示的表达式:
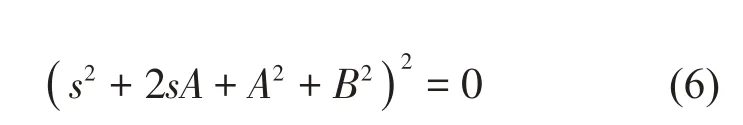
将式(6)展开后并合并s同类项后,可得式(7):
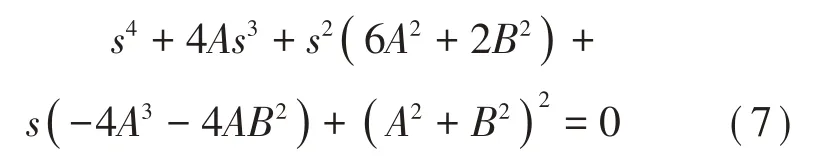
因此,根据待定系数法由式(4)、式(5)、式(7)得到4 个代数方程(电感L的数值是固定的),如式(8)所示,求解这4 个代数方程,即可得到最优等效电阻Ropt以及电容Copt、CS、分流电路的最优阻尼比ζopt、分流电路的最优振荡频率ωdopt。

求解式(8)得到最优参数的解析解如式(9)、式(10)所示:
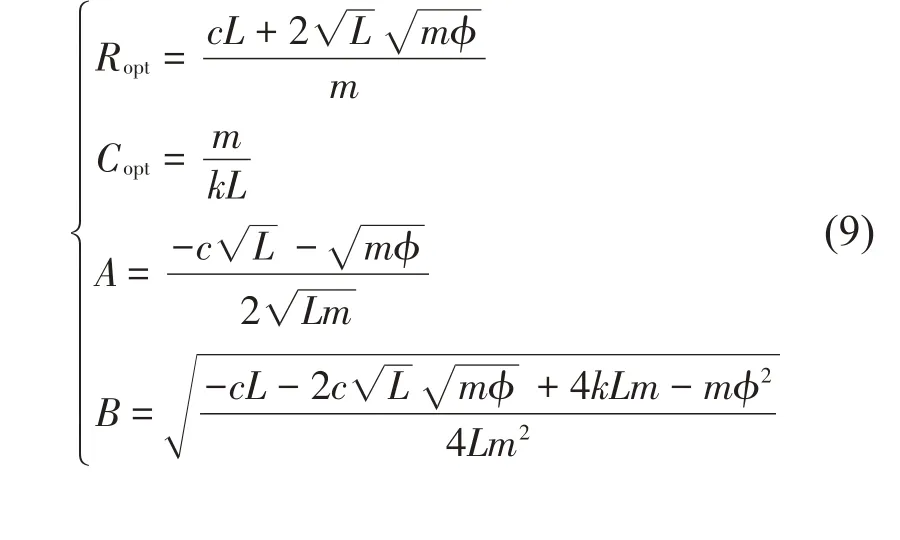

由式(9)可知:分流电路的最优等效电阻Ropt与线圈的电感L和电磁系数ϕ以及主系统的质量m、阻尼系数c有关;最优电容Copt与主系统的固有频率以及线圈电感有关;最优主导极点关于负实轴对称,其中A为最优主导极点的实部,即衰减系数(闭环系统的极点或特征根的实部即为衰减系数),B为最优主导极点的虚部。由式(10)可知:机电耦合系数越大,最优阻尼比越大;不论机电耦合系数取何值,最优调谐比均为1,即只有分流电路的谐振频率与被控结构频率相等时暂态分量的衰减速度是最快的。显然,对于极点配置法的参数优化设计,机电耦合系数的取值不受限制,因此极点配置法的优化设计能解决当机电耦合系数大于或等于2时基于EMSD分流电路参数的最优设计问题。这是其相比于H2优化以及定点理论的优势所在。
3 数值计算
3.1 控制效果对比
第1节中基于EMSD的参数优化所用到参数的具体数值来自文献[7],同时可以根据文献[14],假设主系统阻尼比ζ0=0.05,数值计算参数如表1所示。

表1 电磁分流阻尼器参数
在表1中,机电耦合系数ψ为0.666 7,等效电阻R和分流电路的电容CS为待优化变量,主系统阻尼c由c=算得。根据式(7)可以算出经极点配置法优化所得到的最优电容Copt以及最优电阻Ropt分别为:Copt=0.013 9 F,Ropt=1.738 63 Ω。
同时根据文献[14]提出的采用遗传算法优化EMSD分流电路的思路,根据表1,算得H∞优化条件下的阻尼比为γH∞=0.816 43、调谐比ζ=0.658 31。同时根据文献[3],算得H2优化条件下的最优调谐比以及最优阻尼比分别为:γH2=0.76127,ζH2=0.474 70,故可以算得RH2=0.513Ω,CH2=0.24 F。
若将表1中音圈的电机替换为Supt Motion公司的型号为VCAR0032-0050-00A的直线音圈电机,即将表1 中的线圈电感L设置为0.003 3 H,将电磁系数ϕ设置为7.1 N/A,此时EMSD的机电耦合系数ψ=2.874 6,大于2,结合式(10)可算得,当机电耦合系数大于2时,分流电路的最优阻尼比ζopt为1.733 5。
分别绘制采用上述优化法后的位移放大因子Xn的频率响应,如图2所示。

图2 极点配置法与H2、H∞优化法的控制效果
由图2 可知,定点理论和H2优化更适用于当机电耦合系数小于2 时EMSD 分流电路的优化设计。当机电耦合系数大于或等于2 时,将极点配置法用于EMSD 的分流电路的优化设计,可取得非常好的控制效果,而H2优化和定点理论无法实现。在机电耦合系数ψ=0.666 7时,绘制采用上述优化方法后所得极点复平面图如图3所示。

图3 采用H2、H∞极点配置等优化法后所得极点复平面图
由图3 可知,极点配置法所对应的主导极点距离虚轴最远,因此其衰减系数也最大。这就是说,相比于经典的H∞和H2优化法,经极点配置法优化的系统特征根的实部最大,即时间常数最小,暂态分量也衰减最快。由于H∞和H2优化法对应的衰减速度由它们各自的主导极点的实部所决定,可以算得,极点配置法对应的衰减系数分别大于H∞、H2优化对应的主导极点所决定的衰减系数76.96%、282.47%。
图4所示分别为采用极点配置法优化、H2优化、H∞优化后,系统在单位脉冲信号作用下的时域响应。
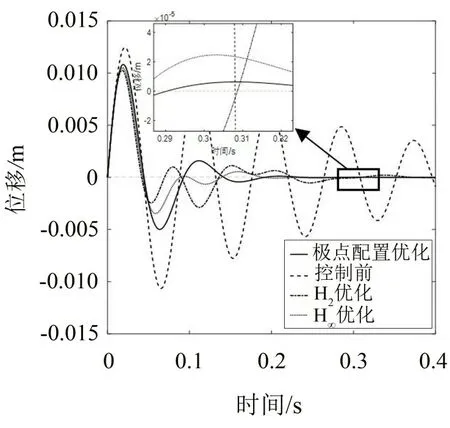
图4 分别采用极点配置法优化、H2优化、H∞优化后主系统在单位脉冲信号作用下的时域响应
给主系统施加一个单位脉冲信号,相当于给了主系统一个大小为1/m(m为主系统的质量)的初速度。由图3 可知,在施加初速度1/m后,经极点配置优化后的主系统的位移衰减最快,即闭环系统的暂态分量单衰减最快,这是极点配置优化法相比于H2优化、H∞优化的优势所在。
3.2 误差分析
将Ropt、Copt分别增加或降低20 %,并代入式(4)求解极点的数值解,然后分别绘制极点在复平面上的位置图,如图5所示。
由图5可知,最优电阻、电容的误差都会导致主导极点从最优主导极点的位置向虚轴方向偏离,这会导致衰减速率下降。

图5 最优电阻、电容增加或降低20%后极点的分布
图6 所示为在单位脉冲信号作用下最优电容、电阻的误差对主系统位移的时域响应曲线的影响。
由图6可知:最优电容、最优电阻的误差会降低主系统位移响应曲线的衰减速度,但是不会导致其发生明显改变;这也直接表明了将极点配置优化法用于电磁分流阻尼分流电路的参数优化,具有相当好的鲁棒性。
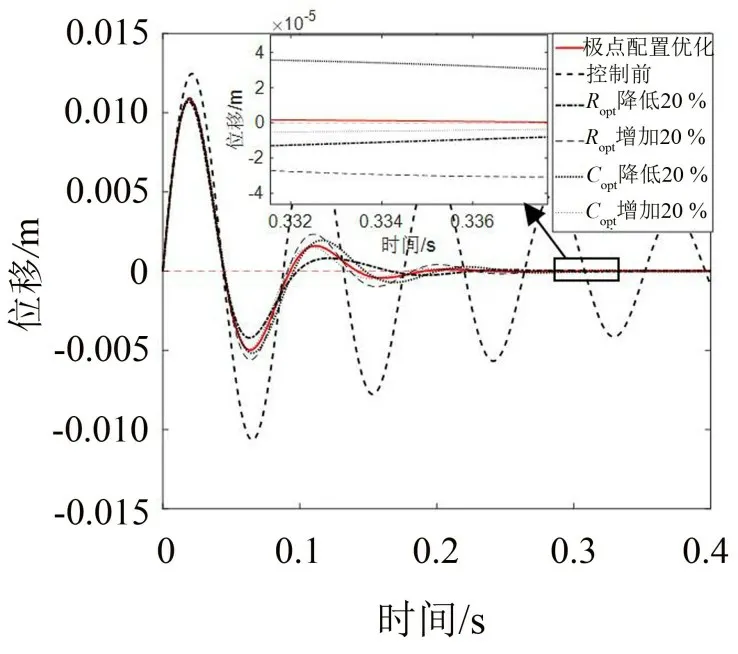
图6 在单位脉冲信号作用下最优电阻、最优电容的误差对时域响应的影响
4 结语
本文通过极点配置法推导出了将EMSD用于单自由度系统的振动控制时分流电路的最优设计参数的解析解。通过数值计算得到了以下主要结论:
(1)使用极点配置法解决了机电耦合系数大于等于2时EMSD分流电路的优化设计问题。
(2)采用极点配置法证明了把分流电路的谐振频率设置为与结构固有频率相等,才能使得系统的暂态分量衰减最快。
(3)相比于H2优化以及H∞优化,极点配置法对应的衰减系数大于H∞优化对应的主导极点决定的衰减系数76.96%,大于H2优化对应的主导极点决定的衰减系数282.47%,因此基于极点配置法的最优设计能使得系统暂态分量的衰减速度最快,这是极点配置法的优势所在。
(4)通过误差分析表明将极点配置优化方法用于EMSD分流电路设计具有正确性、可行性、良好的鲁棒性。
