石油化工装置控制性能监控系统设计和应用探讨
2022-12-20赵霄刘蕴文张晨韵
赵霄,刘蕴文,张晨韵
(1. 中国石化工程建设有限公司,北京 100101;2. 浙江中控技术股份有限公司,浙江 杭州 310053)
现代化大型石油化工装置,特别是千万吨级炼油和百万吨级乙烯工厂PID控制回路数量往往高达数千个,各工艺装置的自控投用率和平稳率直接关系生产的平稳、连续、可靠和安全运行。同时,由于现代企业人力精简,工厂开车调试和运行阶段,单纯依靠操作员人为对PID控制回路进行性能监测、评估与整定优化的工作量巨大,难以做到主动运维,无法满足工艺参数平稳控制的要求。如果PID控制回路无法投用自动、处于开环状态,则只能由操作人员手动调节,不仅劳动强度大、对人员水平和经验要求高,而且由于缺少科学和高效的维护手段,可能直接影响装置运行的平稳性,导致工艺产品质量下降,甚至发生安全事故。
鉴于此,各石化生产企业普遍迫切需要在DCS网络架构中配置功能相对完备的控制性能监控系统CPMS(control performance monitoring system),高效、便捷地实现PID控制回路实时检测、性能批量评估和PID参数整定优化功能,有效提升PID控制回路性能和自控投用率,提高装置整体自动化水平和运行平稳率。
1 典型网络架构
CPMS通常作为分散控制系统(DCS)的高级应用。在新建和改扩建石化工厂(或装置),CPMS通常部署在网络的L3层即操作管理层,考虑到CPMS对于不同品牌DCS的通用性,一般采用标准OPC接口与DCS进行通信。CPMS典型网络架构如图1所示。
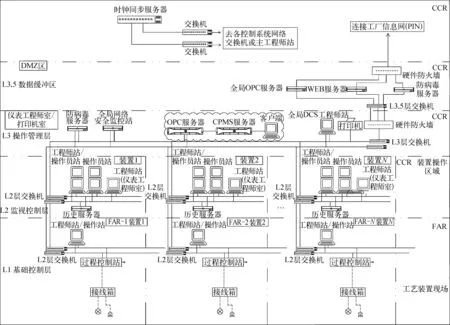
图1 CPMS典型网络架构示意
根据CPMS监控管理PID控制回路的规模,通常多套工艺装置可共用CPMS服务器及其OPC服务器,以尽可能提高软硬件配置效率并节省投资。
2 总体功能架构
CPMS是一套用于基础PID控制回路全生命周期闭环管理的系统,它能够利用控制回路的日常运行数据自动计算与评估其控制性能,使管理者能实时掌握全厂所有装置PID控制回路的运行状态和控制性能,及时发现、识别控制回路中的缺陷,针对评估结果为需要整定PID参数的回路,通过参数整定工具,优化PID参数。整定工具支持在线/离线多种场景的参数整定,充分利用生产过程数据,给出PID回路初始参数,同时采用交互式整定模式,实现闭环状态下的PID参数整定,具备实时性和互动性。CPMS的总体功能架构如图2所示。
相对完备的CPMS的主要功能如下:
1)数据采集与存储。数据采集接口支持OPC DA通信协议,可通过控制系统的OPC服务器实时采集DCS控制回路的实时值、设定值、输出值、状态值、PID参数等数据并高精度压缩存储;支持用户通过客户端登陆,按区域、装置、工段(单元)等不同范围对控制回路进行监控、管理。
2)用户组态配置。通过初始化向导,引导用户快捷地完成组态配置工作;性能评估组态软件提供回路信息管理、回路分组管理功能,评估计划管理与设备模板管理,提供包含组态信息在内的数据备份与还原功能。
3)回路实时监控。对控制回路性能及关键绩效指标(KPI)实施监控和统计分析,帮助管理人员实时掌握企业控制回路的运行情况,实现控制回路的精细化管理。
4)控制性能评估。回路控制性能批量评估,可提供数十种基于频域和时域的回路控制性能指标,并生成专业分析报告;辅助工程师实现控制回路批量管理,提高运维效率。
5)智能诊断分析。针对回路控制器参数,阀门仪表,回路耦合等典型问题给出智能诊断结果和回路运维建议,帮助企业工程师实现回路问题定义,给出运维的专家建议,为回路运维提供信息支持,减小不必要的停工检修,保障企业生产运行的效益。
6)参数常规整定。基于已经产生的过程数据,自动辨识选取有效数据段进行PID参数的整定优化,不对现场产生任何干扰,适用于历史数据中存在较强激励或现场不准添加测试信号的回路,安全智能地实现参数整定工作。
7)交互式参数优化。提供专家经验参数库,不依赖于数据,帮助新开工装置快速进行参数整定,并提供智能交互式整定模式,通过软件交互式迭代优化PID参数,降低整定工具的使用门槛,使得整定优化工作更高效。
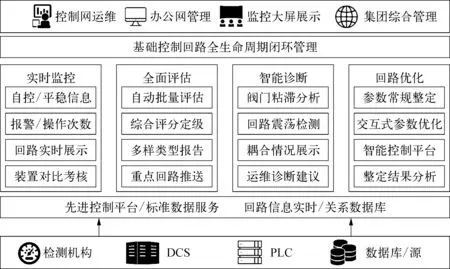
图2 CPMS总体功能架构示意
本文重点阐述CPMS中最为基础和核心的功能——控制性能评估和参数整定优化的基本原理。
3 控制性能评估原理
CPMS能够通过历史数据和实时数据,对控制回路进行在线或离线的性能评估,呈现过程性能综合指标;能够从多个维度对PID控制回路进行性能评估,通过统计计算,得出有关变量的好值率、开环率、饱和率、偏差均值、偏差绝对均值、方差、标准差等参数。
3.1 相关变量计算公式
好值率的计算如式(1)所示:

(1)
开环率的计算如式(2)所示:

(2)
饱和率的计算如式(3)所示:

(3)
偏差均值的计算如式(4)所示:
avg(Xi)=avg(Xi-1)(i-1)/i+
X(i)/ii=1, …,Ndat
(4)
式中:Xi——X中前i个元素;X(i)——X中的第i个元素;Ndat——数据总量。
偏差绝对均值的计算如式(5)所示:
avg(Xi)=|avg(Xi-1)|(i-1)/i+
|X(i)|/ii=1, …,Ndat
(5)
偏差绝对均值是用来计算整体偏差绝对值的均值,即观察偏差的幅度大小。
方差的计算如式(6)所示,采用递推法计算数据的方差:
var(Xi)=var(Xi)(i-1)/i+
(X(i)-avg(Xi))2/ii=1, …,Ndat
(6)
var(X)=var(XNdat)
式中:var——方差;avg——均值。
标准差的计算如式(7)所示:
(7)
PID控制器的控制性能评估,其原理是基于模型-视图-控制器(MVC)控制指标,通过建立最小方差控制器,使得理想地、期望地输出方差最小,作为评价实际控制性能的参考标准。如果实际控制效果的性能评估指标与最小方差控制器输出的参考曲线靠近,则认为控制效果良好;反之,则认为控制性能下降。
3.2 技术路线
CPMS在PID控制回路的性能评估与参数整定优化的技术路线如图3所示。

图3 CPMS控制回路性能评估与参数整定优化流程示意
3.2.1 闭环脉冲响应算法
本文阐述的CPMS主要采用了闭环脉冲响应序列和闭环频率响应曲线来表征控制器的控制性能,其基本原理: 闭环脉冲响应序列可直接用来衡量PID控制器的抑制干扰性能以及设定点跟踪变化情况。在工程实践中,脉冲响应一般是闭环回路的扰动阶跃响应模型,可用来分析闭环回路的性能,如超调量、阻尼比、调节时间、振荡时间等。通过子空间方法辨识得到闭环数据的状态空间模型,再根据该模型计算出闭环脉冲响应序列。状态空间模型形式如式(8)所示:
x(k+1)=Ax(k)+Ke(k)
y(k)=Cx(k)+e(k)
(8)
式中:x(k)——k时刻系统状态,x(k)∈Rn;y(k)——系统输出,y(k)∈Rn;e(k)——预测误差;A——系统矩阵,A∈Rnx×nx;C——输出矩阵,C∈Rny×nx;K——卡尔曼增益,K∈Rnx×ny。
将式(8)转化为式(9)所示预测模型形式:
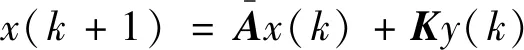
y(k)=Cx(k)+e(k)
(9)

3.2.2 闭环脉冲响应算法性能评估示例
以某PID控制回路FIC804的闭环脉冲响应曲线为例,如图4所示,其中实线为该控制回路的闭环脉冲响应曲线,虚线为闭环参考曲线(图4~图8虚线、实线定义均同)。通过MVC指标,建立理想的最小方差控制器,获得图4的虚线,而实线为实际控制器的性能评价曲线。通过对比,可以看出,实线没有及时地靠近虚线,其衰退至0值的时间相对较长,说明该回路在工况变化或者干扰克服上,响应很慢,主要原因是PID调节速度过慢导致。
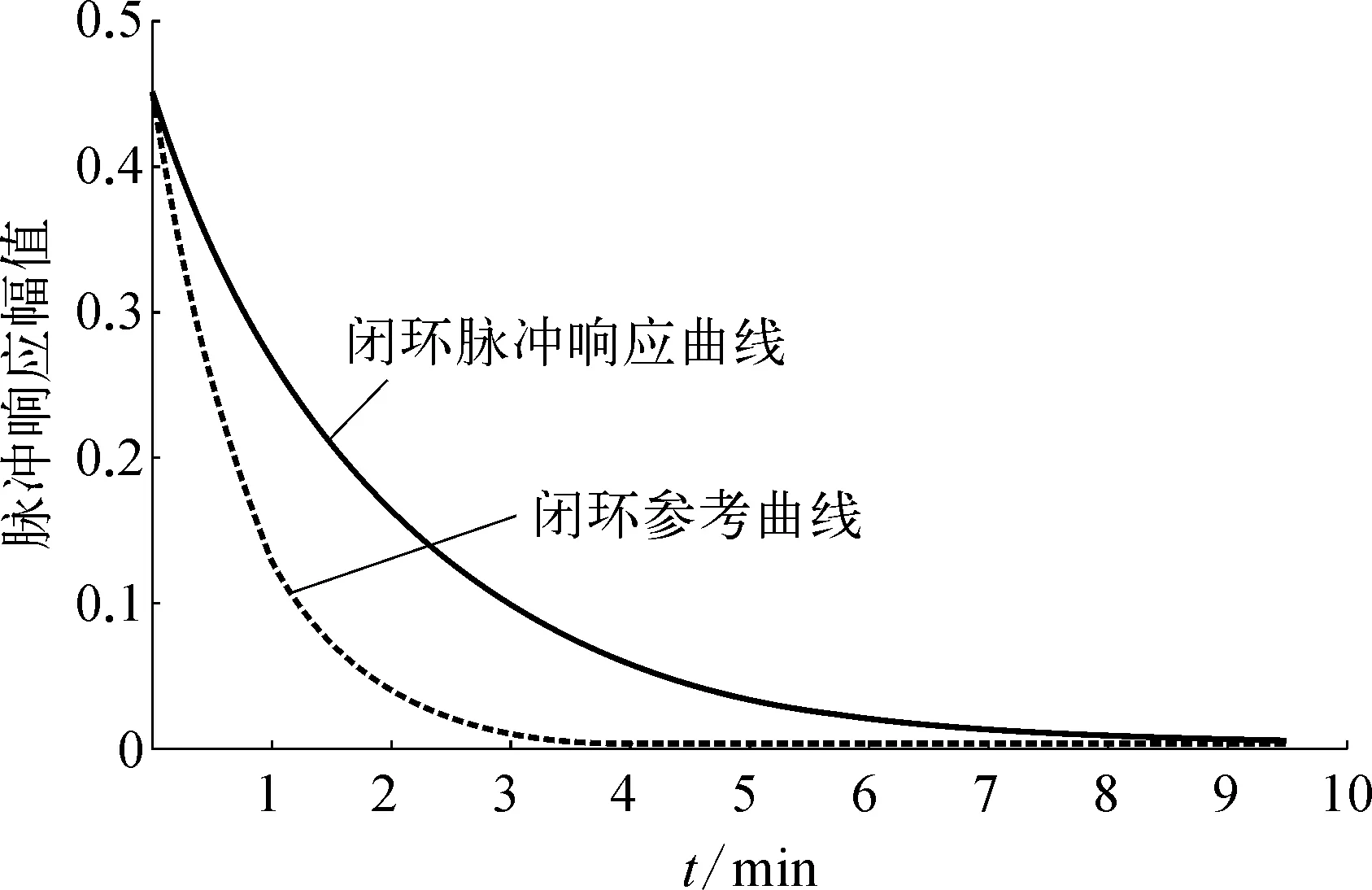
图4 PID控制回路FIC804的闭环脉冲响应曲线示意
以PID控制回路FIC805为例,阐述了PID调控过紧情况下回路所体现出的性能,如图5所示,与图4体现的回路性能相反。图5中,参考曲线体现了该控制回路理想的响应速度情况。当PID控制器调节过于积极时,回路的调节时间大幅减小,快速响应性能提高,但会加剧振荡,导致图5以实线表示的闭环脉冲响应曲线所表现的形式,相比虚线表示的理想控制器参考曲线,该控制器反映的控制性能,存在振荡和超调现象,这种现象可能是由于比例或者积分作用过大所导致。
3.2.3 闭环频率响应算法
CPMS还可通过利用闭环频率响应来分析控制回路PID参数的调节作用和调节强弱,该指标通常以最小方差控制响应图作为基准来进行对比,观察2条曲线在什么频域中相差较大,其基本结论是: 在低频范围内相差较多则通常意味着积分作用不够,或者比例作用较弱;在中频范围内出现大的尖峰波动,则意味着控制器调控过紧(参数调节过猛),或者有振荡扰动模型存在;在高频范围内存在较大差别则表示存在测量噪声。闭环频率响应的算法原理如下。
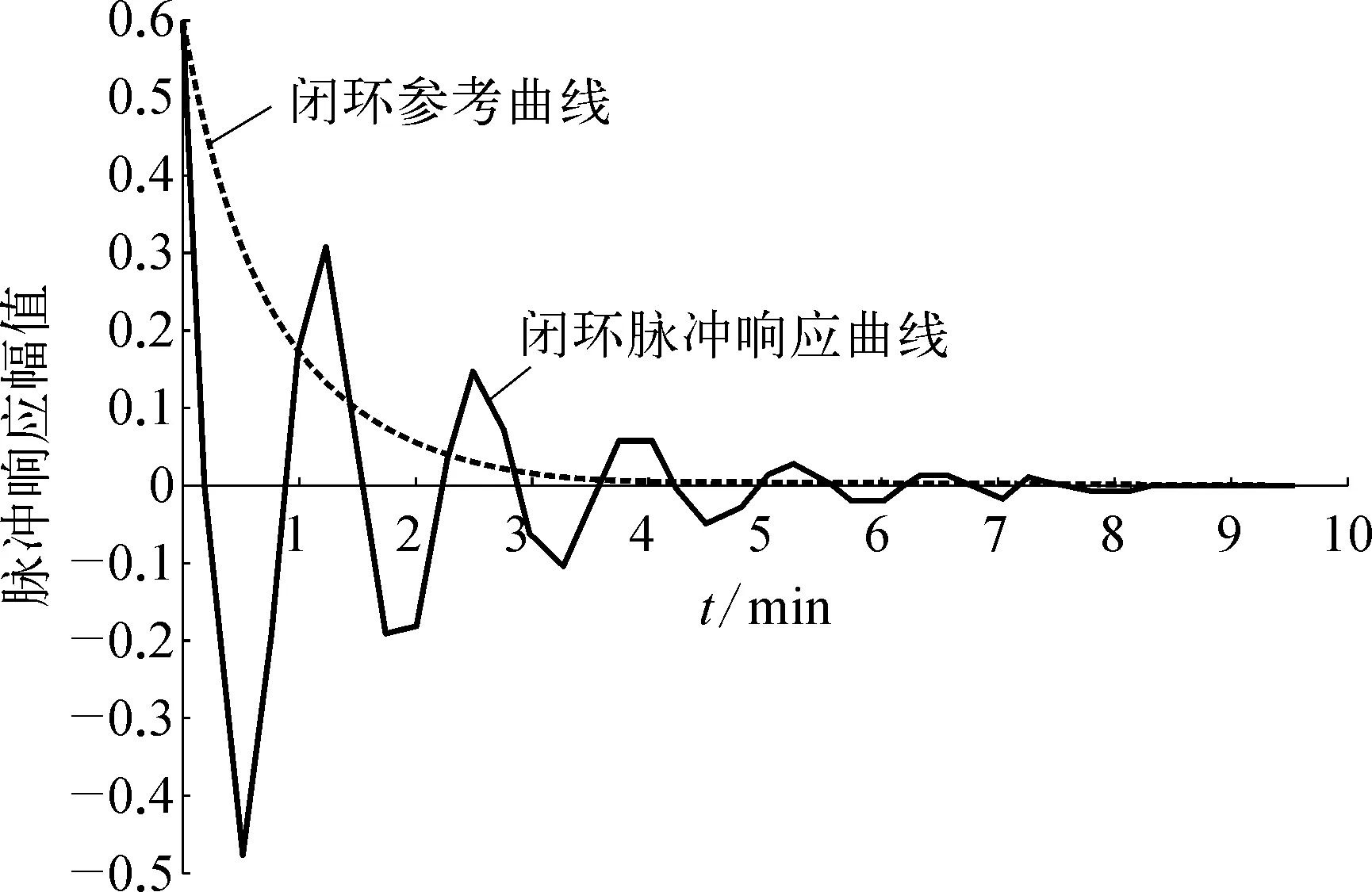
图5 PID控制回路FIC805的闭环脉冲响应曲线示意
对于线性时不变系统,可表示为式(10)所示的脉冲响应形式:
(10)
离散化可得:
G(z)=y(z)/u(z)=h(1)z-1+h(2)z-2+
h(3)z-3+…+h(N)z-N
(11)
频域表示为
G(w)=h(1)e-jTsw+h(2)e-j2Tsw+
h(3)e-j3Tsw+…+h(N)e-jNTsw
(12)
式中:Ts——采样时间。
进一步,化为正弦形式为
G(w)=a-jb
(13)
则有
(14)
3.2.4 闭环频率响应算法性能评估示例
低频段闭环频率响应曲线如图6所示。图6中的闭环频率响应曲线在低频范围内与最小方差控制响应曲线相差较大,说明控制器调控过松,过程过于缓慢,控制作用不够。图6图形右侧高频范围内的振荡是由噪声导致。
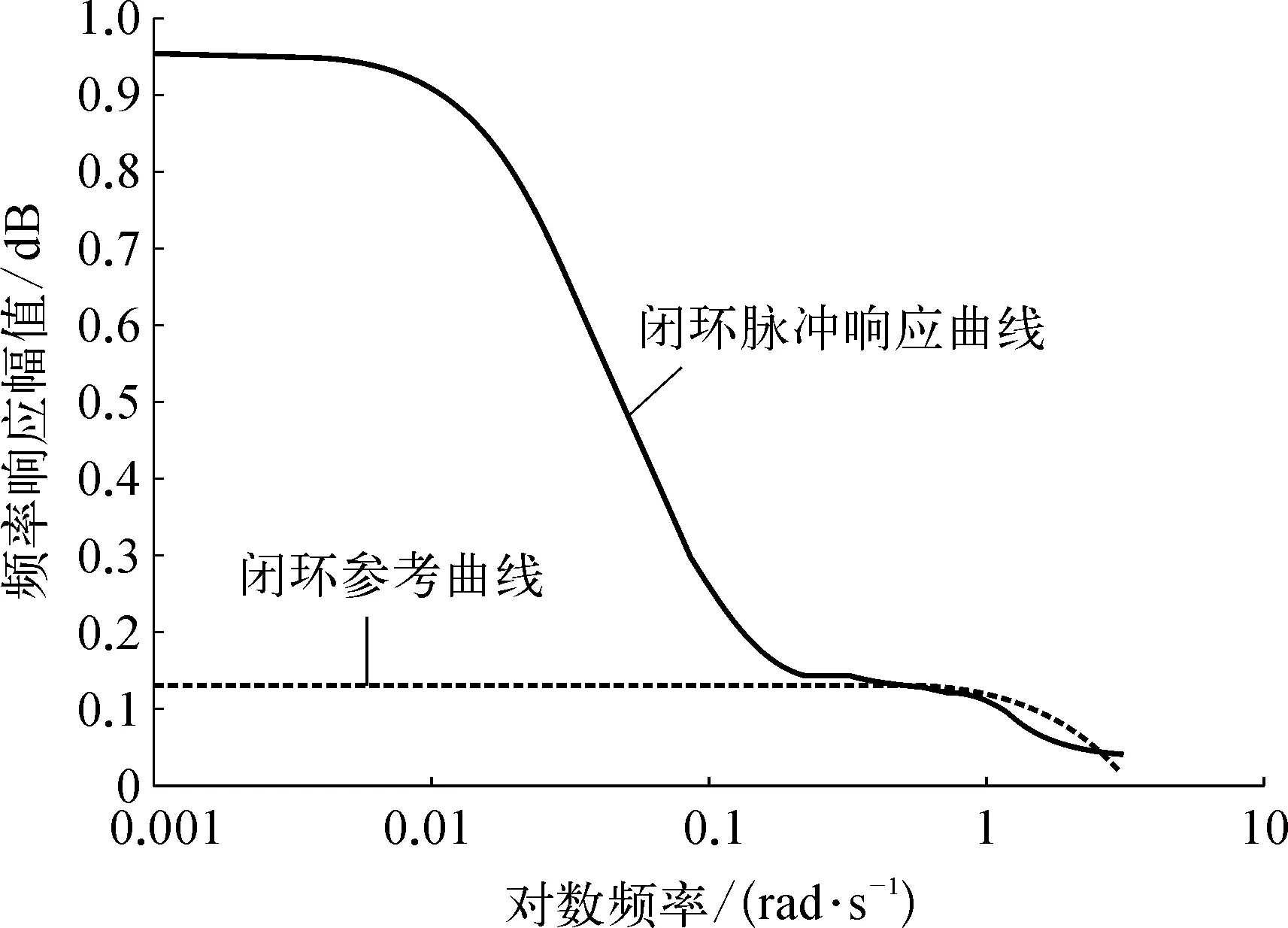
图6 低频段闭环频率响应曲线示意
中频段闭环频率响应曲线如图7所示。图7中的闭环频率响应曲线表示该控制器调控过于积极。该图形在低频范围内非常接近参考曲线值,但在中频范围内存在一个较大的峰值,表示调控过紧,峰值处标明了该点的周期参数值。

图7 中频段闭环频率响应曲线示意
较理想的闭环频率响应曲线如图8所示。图8中的闭环频率响应曲线较为接近参考曲线,控制较为理想。
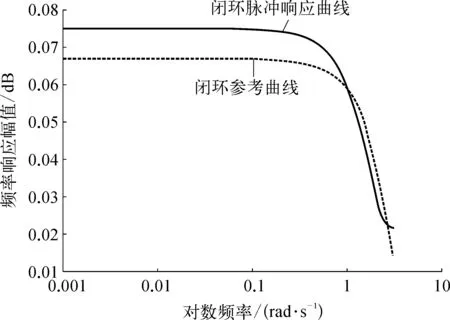
图8 较理想的闭环频率响应曲线示意
4 整定优化方法及原理
本文阐述的CPMS采用基于数据驱动的虚拟参考整定方法实现对PID控制回路参数的整定与优化,其原理如图9所示。
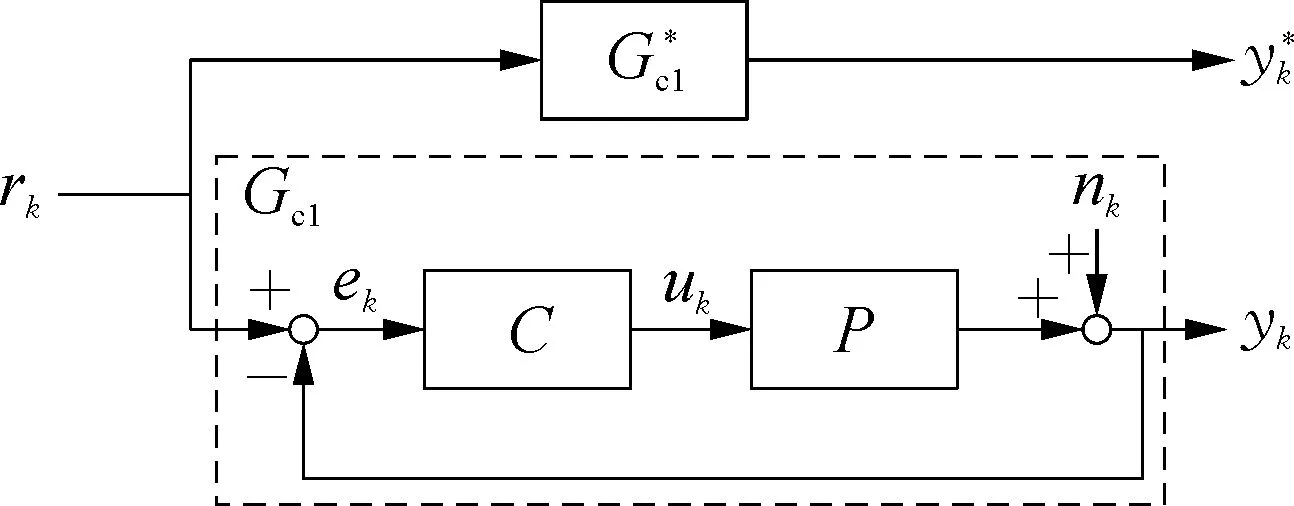
图9 基于数据驱动的虚拟参考整定原理示意
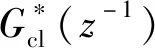
根据实际过程的输入输出测量值和控制器结构,可以推算出参考信号。参考信号通过参考闭环控制系统得到参考系统输出。通过调节控制器参数,期望参考系统输出与实际系统输出的偏差最小,由此考虑目标函数如式(15)所示:
(15)
式中:ε——收敛精度,默认为0.01。
针对标准PID控制器,离散化后,其表达式如式(16)所示:
(16)
式中:K——比例系数;Ti——积分时间;Td——微分时间。
下面定义一个滤波器,如式(17)所示:

(17)
则参考系统输出信号可表示为
(18)
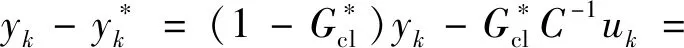
(19)
此处定义滤波信号如式(20)所示:
(20)
目标函数可表示为
(21)
可转化为
(22)
对于给定的f0,f1,f2与PID参数存在如下换算关系和约束范围,且存在唯一可行解:
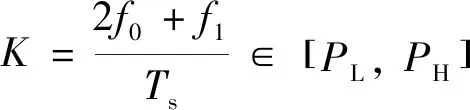
(23)
式中:PL,PH,IL,IH,DL,DH——比例系数约束下限、比例系数约束上限、积分时间约束下限、积分时间约束上限、微分时间约束下限、微分时间约束上限。
此外,合适的参考系统模型对于PID参数整定至关重要,需要能够结合实际动态指标进行设计,据此参考系统离散模型设计为
(24)
则滤波信号表示为
(25)
(26)
其中,参数p1,p2的取值为
(27)

(28)
式中:τ,T——实际系统的时滞时间和时间常数。
基于数据驱动的虚拟参考整定方法,无需迁移大量的历史数据进行学习,支持在线自动交互式整定;与传统通过历史数据的内模整定方法相比,可大幅提高自整定效率,传统方法单个回路整定时间通常为2倍的过渡过程时间。本文所述的方法,60%的回路仅需30%的过渡过程时间就可完成首次迭代整定。
5 典型工艺装置应用分析
以某工程中典型石油化工装置为例,被纳入考核的PID控制回路共计47个,PID控制回路参数整定优化前报告界面如图10所示,参数整定优化后报告界面如图11所示。
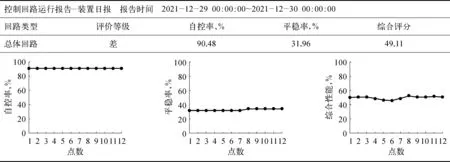
图10 典型工艺装置PID控制回路参数整定优化前报告界面示意

图11 典型工艺装置PID控制回路参数整定优化后报告界面示意
由图10可知,CPMS优化前评估有43个控制回路处于自动模式、4个控制回路处于开环状态,整体自控投运率为90.48%。自控投运率定义为每24 h内回路的手自动状态,CPMS每2 min进行1次记录采样,其计算公式如(29)所示:

(29)
式中:n——24 h内的采样数量720次。
从CPMS的评价分析得到,自动状态的回路控制性能有9.52%评价为“中等”、61.9%评价为“差”,尽管统计报告里自控投用率较高,但是实际控制效果评价并不好,自控平稳率只有31.96%,整体综合评分较低。为了改善该工艺装置整体PID回路的控制性能,需要对回路进行PID参数优化。
由图11可知,PID控制回路性能、自控投用率和平稳率均得到较大改善。CPMS的分析结果显示: 21个控制回路评价为“优秀”,占44.68%;18个控制回路评价为“良好”,占38.95%;5个控制回路为“中等”,占10.03%;2个控制回路为“差”,占4.21%;仅有1个回路因为工艺原因无法投运。
优化PID控制回路参数后的装置,自控投用率提高并稳定在98%左右,自控平稳率提高至88%左右,说明PID控制回路性能的改善对装置平稳、连续、可靠和安全运行有关键作用。部分回路在PID参数整定优化后,控制效果改善情况此处不再赘述。
6 结束语
针对流程工业控制系统操作回路多、操作负荷高的问题,在工程实践中设计并应用CPMS,能够实现对全厂控制回路的实时监控与批量自动性能评估,掌握每个控制回路的健康状况,针对缺陷回路提出维护性意见,提供有效工具整定优化PID参数,最终形成对每个控制回路全生命周期的可靠闭环管理。
通过将CPMS应用于大型石油化工企业,能够大幅提升各装置的自控投用率和平稳率,确保生产装置长期处于最优控制状态;有效减轻操作人员的劳动强度、提高装置的平稳运行和安全水平并降低报警率。未来通过进一步提升CPMS功能,可逐步实现工艺装置的自适应生产,为服务更大规模的流程工业打下坚实基础。
