多通道PID神经网络解耦有源控制算法

吴雪纯，王岩松，郭 辉，郑立辉，袁 涛，朱 瑞

（1.上海工程技术大学 机械与汽车工程学院，上海 201620；2.中国人民解放军陆军装甲兵学院 装甲兵工程学院，北京 100072）

车内噪声不仅影响人们的生活、工作和健康，且影响汽车的乘坐舒适性[1－2]。汽车有源噪声控制(Active Noise Control，ANC)技术在低频噪声控制方面具有明显优势，且具有主动性，可有针对性地控制噪声，对降低驾驶室噪声、提高驾驶舒适性具有明显意义。

有源控制算法是有源噪声控制系统的关键，控制算法的质量决定着整个控制系统的性能。最早的有源控制算法是基于随机梯度法的最小均方(Leastmean-square，LMS)算法，其特点是通过简单有效的递归计算找到最佳权向量。然而，由于忽略了次级扬声器与误差传感器之间的物理通道，导致了时延问题。为了克服次级通道产生的不利影响，Burgess[3]提出了滤波x 最小均方(Filtered-x LMS，FxLMS)算法。在该算法中，在初级噪声输入控制器之前，将次级通道传递函数插入通道中。FxLMS算法因其物理机制清晰，计算复杂度低，实现简单而成为ANC 系统的基础算法。针对FxLMS 算法，也有不同的改进方法，如归一化算法、变步长算法、滤波x滤波u 最小均方(Filtered-x Filtered-u LMS，FxFULMS)算法等[4－6]。改进的主要目的是便于其硬件实现，加快收敛速度，减少自适应稳态误差。

目前，有源控制技术的研究主要集中在单通道噪声的有源控制问题上。由于驾驶室内人员较多，单通道控制系统无法满足多目标区域的降噪要求，为了扩大降噪区域，提升降噪效果，多通道有源噪声控制系统成为研究的重点，即需要多通道自适应控制算法(Multi-channel FxLMS，MFxLMS)。在单通道FxLMS算法的基础上，增加了次级扬声器和误差传感器的数量，成为目前研究中最常用的算法。然而该算法有许多局限性，首先，随着通道数量的增加，算法的计算复杂度急剧增加。对于传统的多通道FxLMS 算法，当参考传感器、扬声器和误差传感器的个数为N时，计算复杂度与N4成正比，因此，随着通道数量的增加，控制系统的计算规模是巨大的。其次，随着通道数量的增加，通道之间的耦合会影响系统的稳定性，任何单一通道的不稳定性都可能导致整个系统的故障。为了克服上述问题，研究人员在多通道FxLMS 算法上取得了重大进展。多通道ANC 算法是针对多通道ANC 系统提出的，其中Chen 等[7]提出了一种新的非线性自适应算法，即对角结构双线性 (Diagonal Bilinear FxLMS，DBFxLMS)算法。仿真结果表明，该算法比2 阶(Volterra FxLMS，VFxLMS)算法具有更好的控制性能。Long 等[8]基于FxLMS 算法和无时延子带FxLMS(Sub-band FxLMS，SFxLMS)算法，提出了两种多输入多输出(Multiple-input and Multiple-output，MIMO)车辆道路噪声控制ANC 模型。仿真结果表明，随着算法所使用的子带数量的增加，基于SFxLMS 的系统与基于FxLMS 的系统相比计算复杂度更低。为了减少前馈多通道FxLMS(feedforward Multi-channel FxLMS，FFMCFxLMS)算法的计算量，Shi 等[9]提出了一种基于多并行折叠分支(Multi parallel folded branches，MPFB)的新架构，使分支被并行化，乘法器和加法器在每个折叠分支中重复使用，从而降低了计算复杂度。

虽然对多通道控制系统的研究多集中在算法复杂度和稳定性上，但通道耦合问题仍需进一步研究。高伟鹏等[10]将一种基于前馈补偿的矩阵解耦优化算法应用于多通道ANC 系统。在次级通道传递函数矩阵前插入解耦矩阵，实现控制信号与误差信号的一一对应。从而使控制系统等价于多个单通道系统，提高了系统的稳定性和收敛速度。矩阵解耦很大程度上依赖于被控对象的精确数学模型[11－12]。由于实际的噪声控制系统是一个非线性、时变的复杂多变量系统，矩阵解耦适用于少数通道，不能满足实际的控制要求。对于多通道控制系统，解耦矩阵的计算更为复杂，降噪效果无法得到改善[13]。因此，多通道ANC系统的解耦方法有待进一步研究。

自适应智能算法的应用是有源控制发展的新趋势，将神经网络算法、模糊算法和自适应算法结合，为振动噪声的有源控制开辟了一条新的途径。神经网络[14－17]以神经元为节点，利用一定的网络拓扑结构来描述几乎任意非线性关系的算法。PID(Proportion Integration Differentiation)神经网络控制方法具有结构简单、工作状态稳定、应用范围广以及可以处理非线性信息的优点，已应用于各种控制系统，如悬架控制系统[18]、轮式机器人[19]等，结果表明，该方法具有良好的动态特性、鲁棒性和抗干扰能力，能有效提高控制速度和控制精度。

以神经网络为代表的智能解耦方法不依赖被控对象精确的数学模型，可以将通道间的耦合问题视为干扰问题进行解耦。本文针对通道耦合问题提出了一种PID 神经网络解耦算法与FxLMS 算法相结合的算法。在传统FxLMS 算法的基础上，利用PID神经网络对ANC系统的控制参数进行调整，获得最优控制。同时，对多通道有源控制系统的解耦和控制问题进行并行处理。将仿真结果与传统FxLMS算法进行了比较。结果表明，本文所提出的方法收敛速度更快，降噪效果更好，更适用于多通道有源噪声控制系统。

1 FxLMS算法

在多通道有源噪声控制中，最常用的算法是多通道FxLMS算法，如图1所示。

图1 多通道FxLMS算法框图

根据前馈有源控制系统的结构，如果控制系统中有I个参考传感器、J个次声源和K个误差传感器，则主次通道数等于I×J和J×K，P(n)表示从噪声源传递到人耳的初级路径。x(n)是采集到的参考信号；假设I个参考传感器接收到的参考信号矢量为：

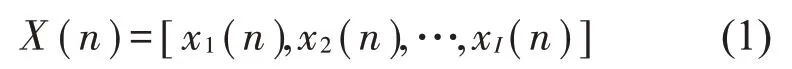
其中：第i个参考信号矢量为：

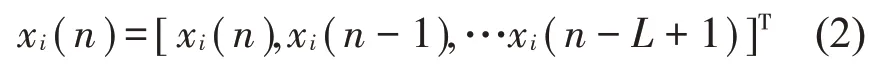
W(n)是控制滤波器，长度为L，其中，第j个滤波器的权系数为：

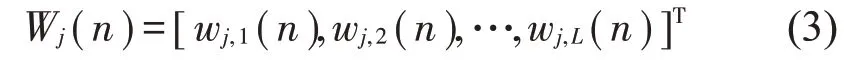
定义控制器输出的次级声信号为：

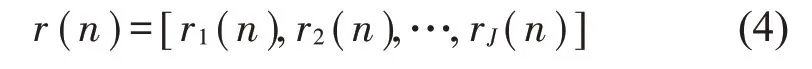
其中：第j个次级声源在第n时刻的输出信号为rj(n)，为了计算方便，这里仅列出系统中只有一个参考传感器的情况，通过计算得到：

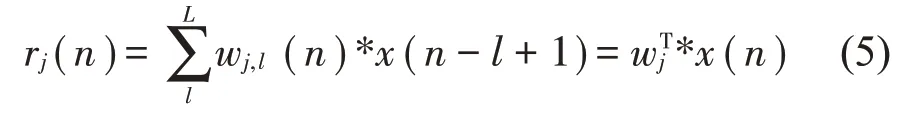
定义h(n)为次级路径传递函数，h′(n)为对次路径信道进行识别得到的h(n)的估计值。次级通道传递函数表示为LJ×K的矩阵：

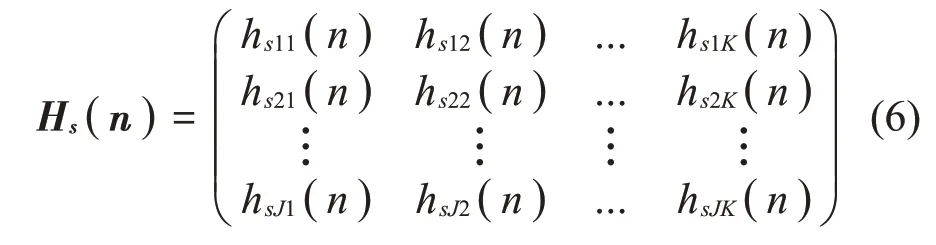
其中元素hsjk(n)可以看作长度为L的滤波器的权矢量，记作：

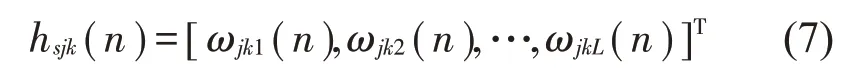
y(n)为输出次级噪声信号，定义y(n)为：

参观完柏林的博物馆岛，稍稍休息一下，我们就启程前往下一站——鲁尔区。鲁尔区曾经是德国重工业集聚的地区。得益于鲁尔区丰富的煤矿，这里上演过德国的工业神话，其单日产煤量曾居世界第一。随着更清洁的油气能源得到推广，煤矿业衰落，鲁尔区的煤矿也被废弃。鲁尔区的工业遗迹如今被改造成了公园，还被联合国教科文组织指定为世界文化遗产之一呢！如今我们漫步其中，一座座巨大的工业机械如同雄伟的纪念碑，给人恍若隔世的感觉。

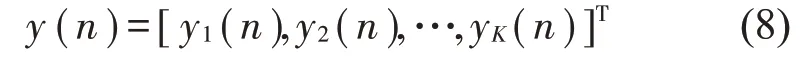
其中：yk(n)为第k个误差传感器接收的J个扬声器发出的声信号经次级通道后叠加信号，以卷积的形式表示为：

则次级声信号对各误差传感器的输入矢量可以写作：

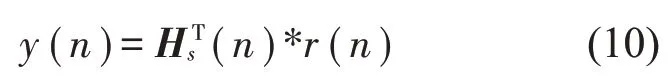
多通道系统通过控制K个误差信号平方和的最小化实现对初级噪声信号的抵消，次级噪声与期望信号相抵消后产生误差信号e(n)。将K个误差传感器的输出组成的权矢量记为：

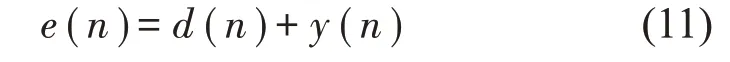
其中：d(n)为期望信号，滤波器权值为：

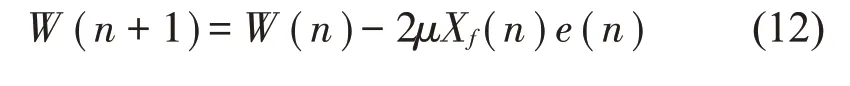
其中：μ为步长，Xf(n)为参考信号自相关矩阵：

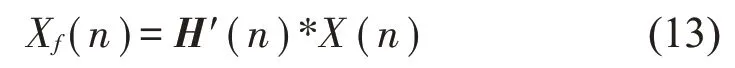
2 PIDNN-FxLMS解耦算法

传统解耦方法严重依赖于被控对象精确的数学模型，难以满足实际的控制要求。而智能解耦方法以神经网络解耦算法为代表，目标是使控制系统的传递函数矩阵为对角阵，将耦合问题作为干扰进行处理，实质上是采用最优控制的方法对目标函数进行参数寻优，由于神经网络结构多输入到多输出的非线性映射关系，可以对控制系统中的耦合部分进行更好补偿，更适用于时变、非线性的对象。因此，本文提出多通道FxLMS 算法结合智能解耦方法(PID neural network FxLMS，PIDNN-FxLMS)算法，解决通道间的耦合问题。图2 为PIDNN-FxLMS 算法框图，图3为PID神经网络结构图。

图2 PID神经网络解耦算法框图

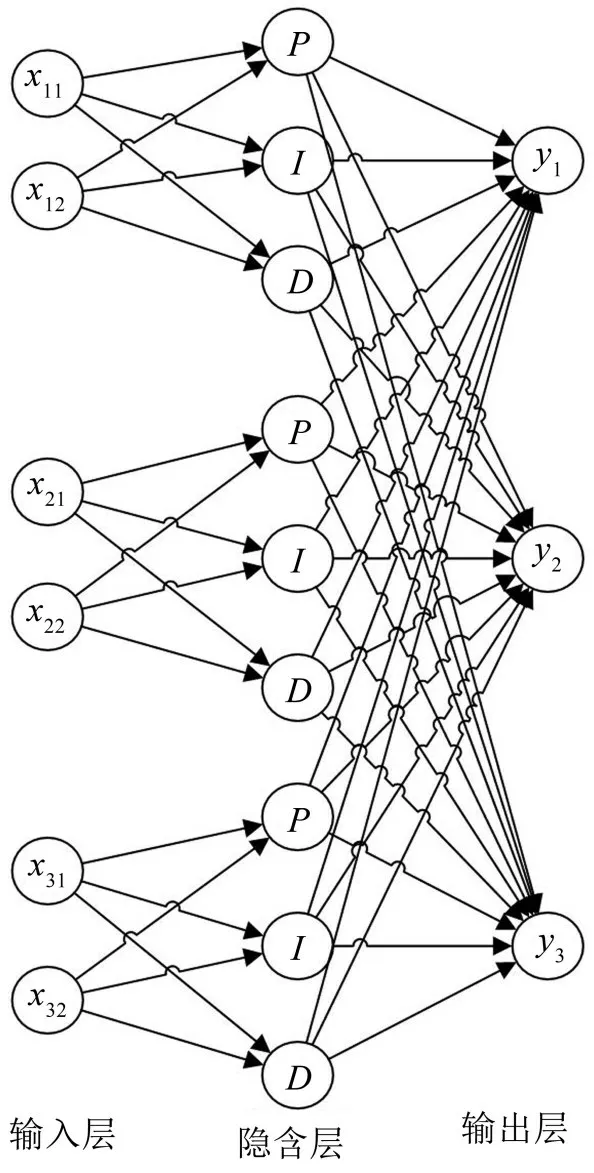
图3 PID神经网络结构图

如图3所示，PID神经网络可分为3层：输入层、隐含层和输出层。具有m个控制变量的PID神经网络包含m个平行的子网络。各个子网络相互独立，而且通过网络连接权重相互连接。

由图3可看出每个子网络的输入层有两个神经元，它们接收控制量的目标值和当前值。变量x11、x21和x31是控制量的目标值，变量x12、x22和x32为控制量的当前值。每个子网络的隐含层由比例单元P、积分单元I和微分单元D组成，分别对应PID控制器中的比例控制、积分控制和微分控制。隐含层中每个神经元的输出为u。每个子网络的输出层只有一个神经元，即y1、y2和y3。此外，s为并行子网络的序号，i为子网络中输入层神经元的序号，j为子网络中隐含层神经元的序号，k为子网络中输出层神经元的序号。对于多层神经网络，ωij是输入层和隐含层之间的权重，ωjk是隐含层和输出层之间的权重。

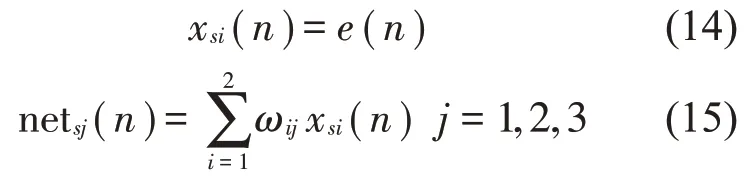
则比例神经元、积分神经元和微分神经元的输出为：

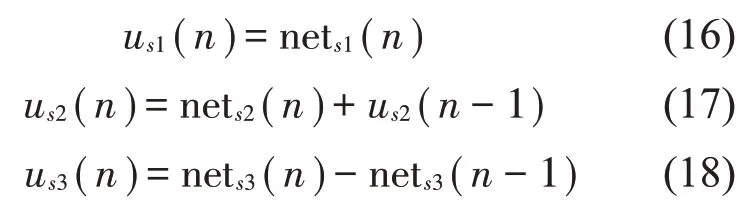
输出层计算的结果可表示为：

误差更新公式可以写成：

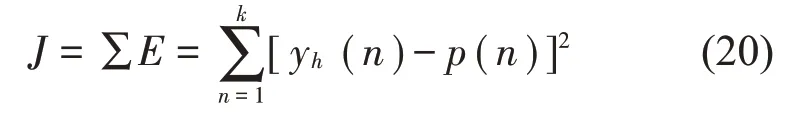
输出层到隐含层、隐含层到输入层之间的权值更新如下：

其中：η2为学习率。

PID 神经网络的计算过程可分为两个步骤：网络的前向计算和后向误差传递以及权值修正。重复这个过程，直到消除误差。输入信号通过一层时，利用输入信号根据当前节点的权值和函数计算出相应的权值。输出结果被转移到下一层。当网络输出与期望输出不一致时，将输出与期望输出之间的误差信号反向传输，将返回误差结果作为修改权值的依据。该控制系统可根据权重控制输出信号，实现最小的均方误差。

PID控制可以消除稳态误差，提高响应速度，而为了提高PID控制器的性能，需要调整比例单元、积分单元和微分单元之间的关系。然而，这并不是一个简单的线性关系，而是在一个不断变化的非线性组合中寻找最佳关系。神经网络可以逼近任何非线性函数，其结构和学习算法简单明了，可以通过网络找到PID 控制最优参数。因此PIDNN-FxLMS 算法具有参数可快速收敛的优点，利用最优控制原理可实现多通道解耦控制。

3 基于实测数据的算法仿真

本节采集怠速状态与静止状态下的汽车车内噪声与振动信号进行实验。试验车辆为国产某品牌家用轿车，采集数据时车窗处于关闭状态，应用的噪声采集设备为SIEMENS 生产的LMS SCADAS Mobile，实验采集时间为10 s。为确保采集数据包含原噪声中全部信息，进行数据采集时选择了一个较大的采样率16 384 Hz。采集时采用三通道结构，通道一为驾驶位右耳噪声，通道二为副驾驶位中间位置噪声，通道三为后排中间位置噪声。为提高仿真精度，可通过离线次级路径建模对次级路径传递函数进行拟合，可得到三通道次级路径传递函数如表1所示。

表1 三通道次级路径拟合结果

初级噪声时域以及频域图如图4、图5 所示，从频域图可以看出，3 个通道的低频噪声（20 Hz～500 Hz）幅值较大，通道一、二中频噪声（500 Hz～2 000 Hz）幅值较小，而通道三的中频噪声略大于前两个通道。

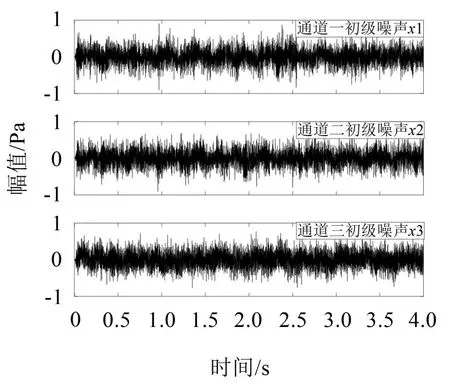
图4 初级噪声时域图

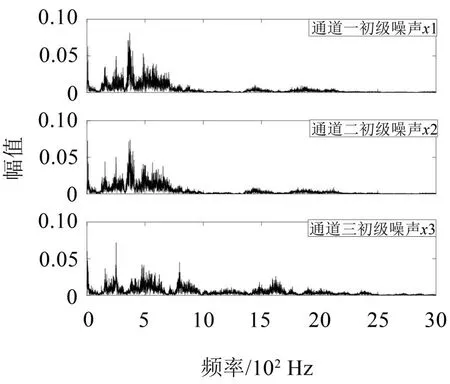
图5 初级噪声频域图

为了验证所提出的多通道有源控制算法的收敛性，利用Matlab进行仿真，将PIDNN-FxLMS算法与传统FxLMS算法进行对比，见图6至图11以及表2，比较控制后误差信号的幅值和控制过程中算法的收敛速度。在仿真中，设置滤波器长度为16，步长μ为0.01，学习速率η2为0.001。两种算法的控制结果如图6至图9所示。

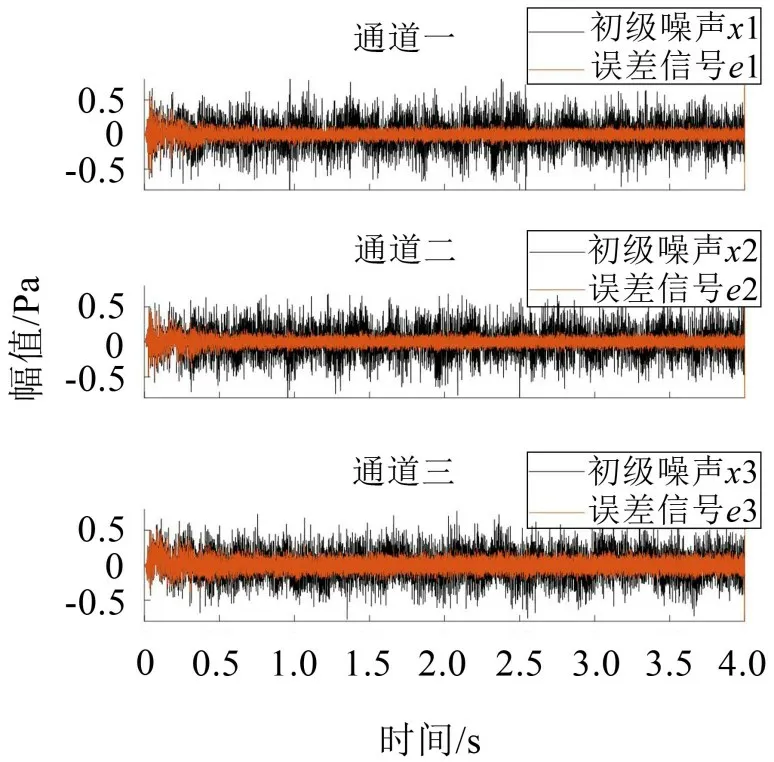
图6 FxLMS算法的噪声时域控制效果

图7 PIDNN-FxLMS算法的噪声时域控制效果

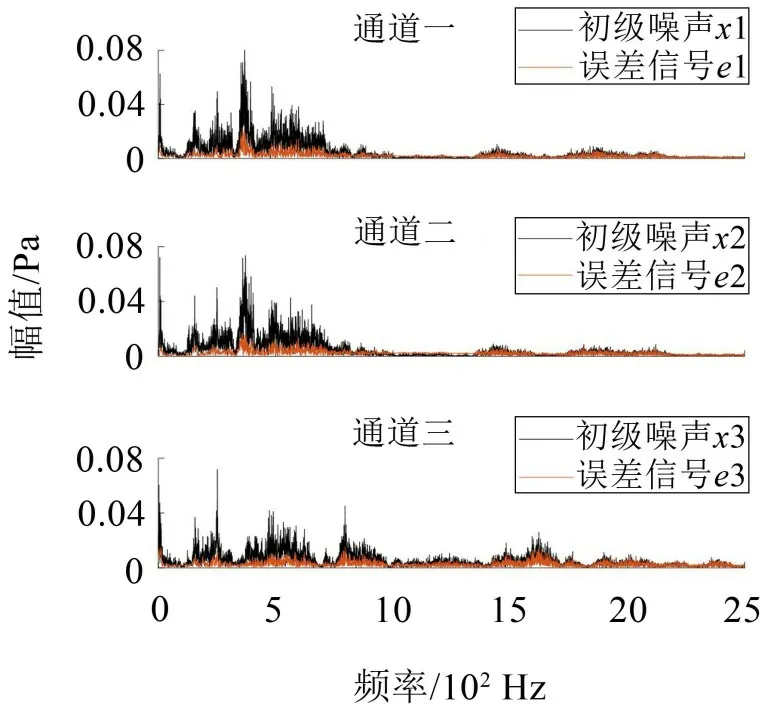
图8 FxLMS算法的噪声频域控制效果

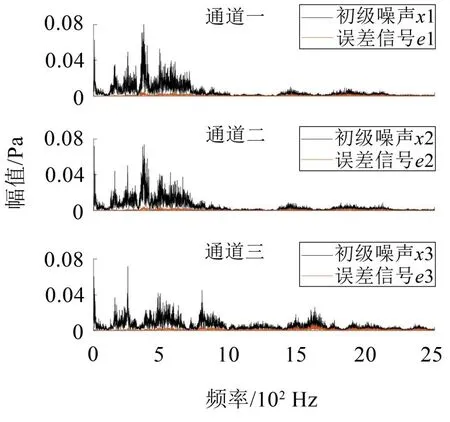
图9 PIDNN-FxLMS算法的噪声频域控制效果

图10 PIDNN-FxLMS算法与FxLMS算法的噪声控制时域对比

图11 PIDNN-FxLMS算法与FxLMS算法的噪声控制频域对比

图10 比较了两种算法的误差信号。两种算法控制前后的噪声信号幅值以及计算时间如表2所示。

表2 两种算法误差信号结果对比

图6、图7为FxLMS算法与PIDNN-FxLMS算法的噪声时域控制效果图，可以看出两种算法对噪声都具有良好的降噪效果，残余噪声信号幅值相比于原始信号都有很大程度降低。

图8、图9为FxLMS算法与PIDNN-FxLMS算法的噪声频域控制效果，可以看出对于低频噪声，传统FxLMS 算法具有一定的降噪效果，而对于中频噪声，降噪效果不明显，在800 Hz～1 500 Hz降噪幅度较小，频率大于1 500 Hz 时残余误差信号幅值接近初级噪声，而PIDNN-FxLMS 算法对低频噪声和中频噪声的降噪效果更好，残余误差信号幅值更低，且对于初级噪声幅值较高的频率也具有很好的降噪效果。

图10、图11为两种算法的噪声控制时域与频域对比结果，表2 为两种算法误差信号的平均幅值以及收敛时间、计算时间，由此可以看出传统FxLMS算法三通道误差信号幅值分别为0.06 Pa、0.07 Pa、0.12 Pa，且在约0.5 s时趋于收敛，而PIDNN-FxLMS算法三通道误差信号幅值分别为0.03 Pa、0.04 Pa、0.07 Pa，且在约0.1s时趋于收敛，收敛速度明显快于传统算法。从频域图可以看出，PIDNN-FxLMS算法对低频噪声都具有更好的降噪效果。这是由于传统FxLMS算法虽然考虑到通道间的相互耦合，但并没有解决此问题。神经网络具有较强的自适应和自学习能力，且能够以任意精度逼近非线性函数，并能处理非线性问题，消除通道间的相互干扰，以起到解耦的效果。因此，采用PIDNN-FxLMS 算法可以获得更好的控制性能。另外，PID控制器中的3个控制单元在比例控制的基础上相互补足，积分控制可以消除稳态误差，但会增加超调量，而微分控制可以提高系统的响应速度，减弱超调趋势。在计算时间方面，由于与PID 神经网络算法相结合，使得算法的计算量在一定程度上有所增加，计算时间相比于传统FxLMS算法也有所增加，但降噪效果不管是对于低频噪声还是中频噪声都得到了明显提升。因此，PIDNN-FxLMS算法具有更好的控制性能，收敛速度也更快，对于增强有源噪声控制系统的实时性控制更加有效。

4 结语

考虑到在多通道ANC系统中，随着通道数量的增加，多通道耦合的存在会影响控制系统稳定性，本文将PID神经网络算法应用于多通道ANC系统，提出了一种新的PIDNN-FxLMS。该算法将控制与解耦问题结合，一起进行求解，由于神经网络具有独特的非线性映射结构，几乎可以逼近任何非线性函数，可消除通道间的相互干扰，达到解耦的目的，同时提高降噪效果。此外，神经网络独有的并行神经元结构使得计算权值系数的时间较短，与PID 控制相结合，更是提高了控制系统的收敛速度。通过仿真计算与传统FxLMS算法对比分析，结果表明，PIDNNFxLMS 算法对于低频以及中频噪声都具有更好的控制效果即更小的残余误差以及更快的收敛速度，更适用于车内有源噪声控制，可为车内多通道有源噪声控制提供一种更有效的方法。