偏心旋转阀气动噪声产生及控制机理研究
2022-12-20郝娇山刘柏圻杨恒虎王伟波
廖 静,郝娇山,刘柏圻,杨恒虎,王伟波
(1.重庆川仪自动化股份有限公司 技术中心调节阀研究所,重庆 400707;2.重庆川仪调节阀有限公司,重庆 400707)
偏心旋转阀作为煤气化装置中的关键调节阀,在气化炉升压、泄压、保压运行、停车放空及氮气置换的工艺操作环境中,承担着背压调节、控制系统压力、安全放空等重要作用[1]。但其在功能实现过程中可能产生的噪声不仅对环境产生污染,还会影响阀门本身性能,同时,伴随噪声产生的结构振动将造成相邻管路和设备疲劳损伤,甚至可能导致安全事故,该阀门的高噪声问题在煤气化领域日益受到关注[2]。因此,研究偏心旋转阀气动噪声的产生机理,是实现噪声控制的重要基础。
近年来,随着计算机能力的大幅提高以及计算流体力学和工程声学软件开发日益成熟,国内外学者在阀门气动噪声问题上进行了大量数值模拟研究。气动噪声的数值模拟方法主要有气动声学方法(简称CAA)、莱特希尔声类比方法(Lighthill 声类比)和混合计算方法(Hybrid Method)[3]。Wei 等[4]采用基于宽带噪声源模型的直接模拟方法对高参数减压阀的内部流场和声场进行了数值分析,确定了射流产生的涡流和激波的交替形成和脱落是气动噪声产生的主要原因。孟令雅等[5]采用直接模拟方法和混合模拟方法计算气流流过球阀产生的气动噪声,结果表明阀门的噪声源为偶极子声源和四极子声源。徐号钟等[6]采用基于Lighthill 声类比模型的CFD/CAA 多步骤混合计算方法对截止阀腔内气动声学共振特性进行数值计算,得到了阀门腔内声共振特性对噪声的影响,以及小孔消声装置对阀门内流动声源的控制效果。孙长周等[7]通过Lighthill 声类比方法计算得到某型号流量调节阀内壁面处的声压,通过声振模型获得阀门外部声场以及外部监测点的声压级频谱曲线。综上所述,阀门气动噪声的数值模拟大多采用基于Lighthill声类比模型的混合计算方法,该模型对于低马赫数气动噪声的计算效果较好,但对于偏心旋转阀的高马赫数气动噪声的数值模拟需采用考虑了声源区域流体的可压缩性和声辐射区域流体的对流效应的Möhring 声类比模型。该模型已应用于在发动机和压气机的噪声预测[8-9],但有关其在阀门领域中的应用文献较少。
鉴于此,本文选取煤气化装置中用于合成气洗涤塔高压差压力调节的偏心旋转阀为研究对象,按照实际工况参数建立偏心旋转阀及附属管道的有限元分析模型,应用ANSYS Fluent 2020 R2 流体仿真软件和MSC Actran 15.0 声学仿真软件开展声流固耦合数值模拟计算。通过Conval 11.0阀门选型软件求解气动噪声标准值,验证数值模拟方法的可靠性。采用加装降噪孔板、减小流量和增大进口压力的降噪措施研究噪声控制机理,并为偏心旋转阀的高噪声问题提供合理的降噪设计方案。
1 多步骤混合计算方法
本文采用多步骤混合计算方法开展偏心旋转阀气动噪声的数值模拟计算,应用ANSYS Fluent计算流体力学软件中的SST-DDES模型进行瞬态流场计算,获得压力、速度、密度等流场信息,然后通过MSC Actran声学软件的Möhring声类比模型将流场信息转换为气动噪声源,通过网格映射将平均流场信息、气动声源和湍流壁面压力映射到声场流体域网格上,并采用傅里叶变换进行时域和频率间变换,如图1所示。
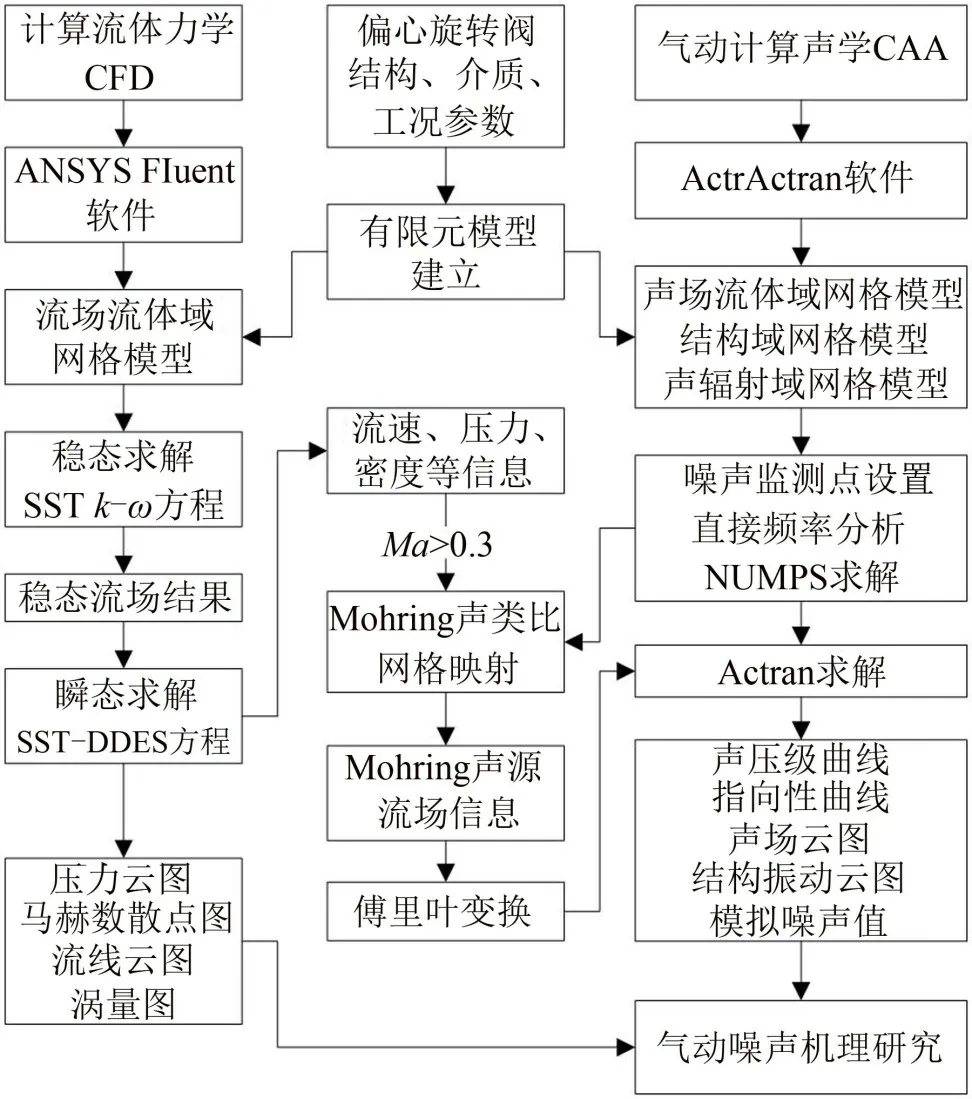
图1 多步骤混合计算方法流程图
1.1 控制方程
SSTk-ω湍流模型方程[10]如式(1)所示:
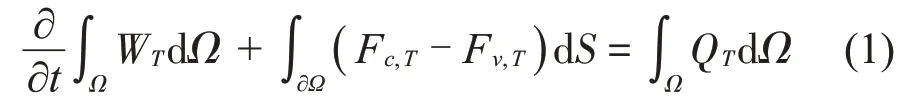
式中:WT为守恒变量;Fc,T为对流项;Fv,T为黏性项;QT为湍流运输方程的源项。
基于SSTk-ω两方程湍流模型定义DES 尺度,替换k方程中的耗散项实现SST-DDES模型[11],如式(2)所示:

式中:Δ为3 个方向上的最大网格步长;f1由湍流模型给出
声类比方法最初由Lighthill[12-13]提出,通过对N-S方程进行变换重组,将其写成波动方程格式,忽略了流动对声波的影响。Möhring[14]使用类似方法对此进行了扩展,提出了Möhring声类比模型,该模型考虑了声源区域介质的可压缩性和声辐射区域介质的对流效应,更适用于高马赫数(Ma>0.3)气动噪声计算[8]。Möhring声类比方程如式(3)所示:
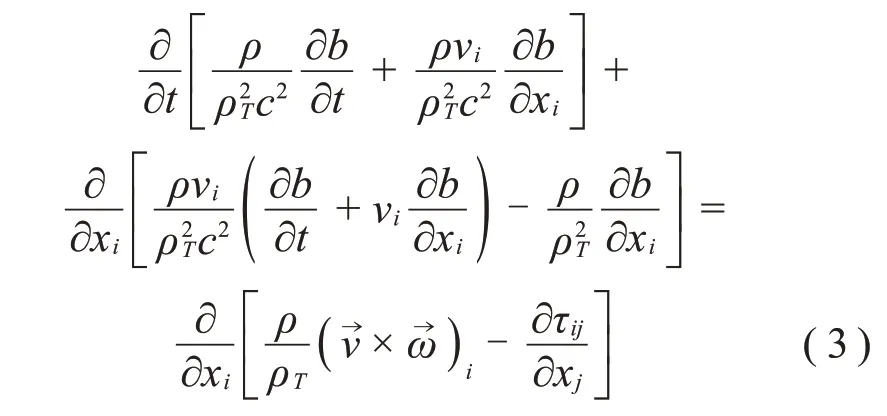
式中:ρ为密度;ρT为总密度;vi为速度;b为标量焓值;c2=为声速为旋涡。
式(3)中等式左边(LHS)为声传播项,右边(RHS)为声源项,对RHS 进行傅里叶变换,得到Möhring 声类比频率方程,然后应用有限元法、部分积分法及高斯定理得到有限元方程,如式(4)所示:


1.2 几何模型和工况参数
偏心旋转阀的几何模型由阀体、阀座、阀杆、V球、进口管道和出口管道组成,材料简化为结构钢,密度为7 850 kg/m3,泊松比为0.3,杨氏模量2.1×1011Pa。阀门公称通径为DN150,额定流量系数为380,流量特性曲线为近似等百分比,压差比系数为0.4,阀门类型修正系数为0.25,压力恢复系数为0.9,介质由阀座方向流入。建立几何模型时忽略了介质非流动区域结构,并简化填料部件、底轴、底盖等结构。考虑气动噪声监测点位置要求[15]和工业管道对阀门的影响,进口管道长度为2倍管道公称通径[16],出口管道长度为1.3 米[17],总长共计1 828.5 mm,如图2所示。

图2 偏心旋转阀几何模型
合成气洗涤塔的高压差压力调节用偏心旋转阀以合成气为介质[18],介质参数和实际工况参数均按某煤气化装置实际参数选定,摩尔质量为24.344 kg/kmol,进口压力为2 MPa(G),出口压力为0.5 MPa(G),流量为10 kg/s,温度为180℃,相应的等熵指数为1.38,操作密度为13.5 kg/m3,黏性系数为1.54×10-5kg/(m·s),声速为469.23 m/s。
1.3 网格模型
网格模型包括瞬态流场模拟所需的流体域网格和声场模拟所需的声流体域网格、结构域网格和声辐射域网格,如图3所示。

图3 声场网格模型
流体域网格采用poly-hexcore 网格划分技术进行划分,在近壁面的流动区域划分边界层,采用最小面网格尺寸Smin细化处理流动变化剧烈区域,采用最大面网格尺寸Smax控制网格数量。通常网格数量越多计算精度越高,但计算时间越长,网格单元达到一定数量后计算结果基本不变,这被称为网格无关化[19]。本文以流量值为网格无关化的衡量指标。如表1 所示,采用3 组网格尺寸建立40°开度的流场有限元模型a、b、c,基于上述介质和工况参数,选用SSTk-ω湍流模型开展稳态流场数值模拟,最大流量误差为0.05%。因此,考虑模拟计算精度、时间成本和工作量,本文认为模型b已达到网格无关化。
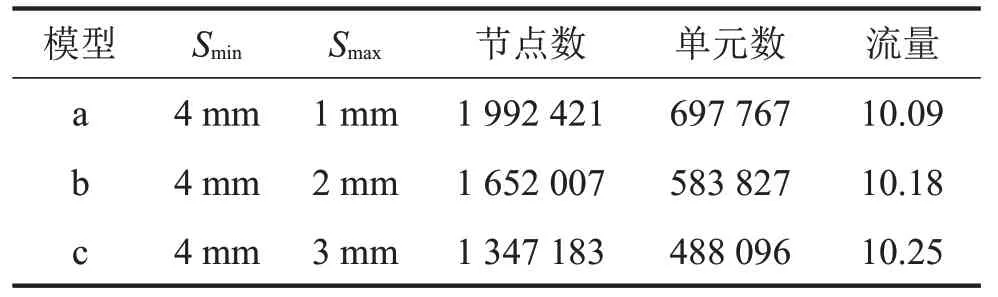
表1 流场流体域网格无关化模拟结果/(kg∙s-1)
声流体域网格和声辐射域网格采用MSC Actran软件的波长计算工具和网格划分工具进行处理,得到最高频率为5 000 Hz 的声场流体域网格单元大小为10 mm,单元数为399 130,节点数为89 976,声场辐射域网格单元大小为20 mm,单元数为514 739,节点数为119 417,满足了最高频率对应的声波波长内划分6~8 个单元的要求。考虑在气动噪声计算中结构域网格与声流体域的流固耦合,以及与声辐射域的声振耦合作用,结构域网格密度需满足振动波长内8~10 个网格单元的要求,本文采用ANSYS Meshing软件划分结构域网格模型,设置网格单元大小为5.5 mm,单元数为676 218,节点数为160 829。
1.4 数值模拟监测点
为了监测瞬态流场中压力、流量、马赫数等参数随采样时间的变化趋势,同时获得偏心旋转阀气动噪声模拟值和声指向性曲线,本文以偏心旋转阀阀体中心为原点,以介质流动方向为X轴正方向,以竖直向上的安装方向为Y轴建立坐标系。流场对称面为XZ平面,流场监测点“B”坐标为(1114.5,0,0)。气动噪声模拟值监测点“A”坐标为(1 114.5,1 084.15,0),符合文献[11]中的标准规定;以监测点“B”坐标为圆心,以1 084.15 mm 为半径建立360 个监测点,用以观察气动噪声在远离阀门出口1米处的声指向性,如图4所示。
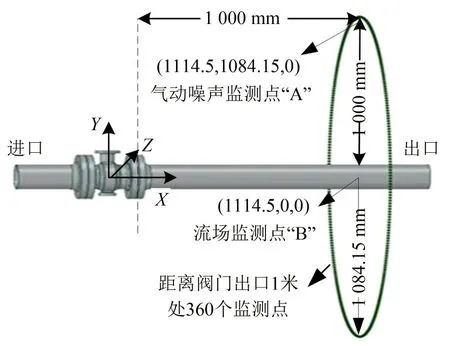
图4 数值模拟监测点示意图
2 数值模拟结果与分析
2.1 流场数值模拟结果与分析
采用多步骤混合计算方法建立40°开度偏心旋转阀及附属管道的有限元模型(简称为N 模型),以合成气为介质模拟稳态流场数值,以实际进出口压力为边界条件,开启能量方程,选用SSTk-ω湍流方程,将监测“B”坐标点的压力脉动曲线作为流场收敛性判断依据。将收敛后的稳态流场结果作为瞬态流场计算的初始值,选用SST-DDES模型,设置瞬态流场采样步数为800 步,采样步长为0.0001 s,根据Nyquist 采样定理可知,声场计算的最大频率为5 000 Hz,最小频率为12.5 Hz。
提取0.04 s 时XZ平面的马赫数,如图5 所示。合成气以2 MPa(G)进口压力流入进口管道,此时马赫数约为0.1,合成气处于低马赫数流动状态,因管道内面积不变,该区域内的马赫数基本保持恒定;随后,合成气进入阀体内腔区域,马赫数迅速上升至约1.7,到达出口管道后马赫数逐渐趋于稳定,马赫数约为0.35。由文献[12]可知,高马赫数气体所在的区域极容易产生冲击波、喷射流、旋涡流等凌乱流体,这种流体产生的气动噪声沿着出口管道传递到各处,严重时将因振动过大而破坏管道系统。
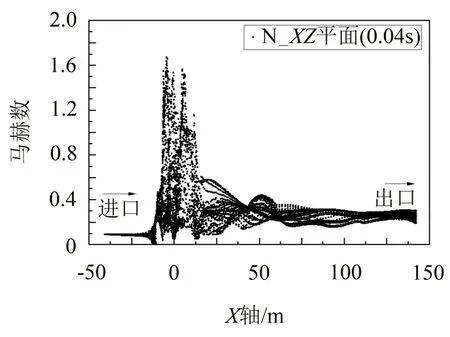
图5 0.04s时XZ平面的马赫数散点图(N模型)
N 模型在0.04 s 时的流线云图和涡量图如图6所示。流线云图采用150 条流线绘制,涡量图采用Q-Criterion方法进行绘制。流线以恒定流速进入阀座区域,V球的阻挡使得流动方向发生改变,因阀体内腔受限,在挤压效应的作用下,狭窄区域的流速迅速增加至533.6 m/s,V 球两侧位置均出现了冲击射流和回流现象,围绕射流的流线分布较混乱。大量的涡旋结构分布于阀体内腔和出口位置并呈脱落现象。这些涡旋对偏心旋转阀内部结构产生的不平衡力容易引起振动,涡旋中心容易产生气穴;涡旋脱离的频率与阀门及附属管道结构的固有频率接近或相同时容易产生共振现象,这些都是气动噪声源[20]。

图6 0.04 s时的流线云图和涡量图(N模型)
2.2 声场数值模拟结果与分析
提取2.1 小节瞬态流场的速度、压力和密度信息,采用Möhring 声类比方法将流场信息转换为声源。采用直接频率分析方法,分别设置声场流体域网格和声辐射域网格为有限域组件,结构域网格为固体域组件,声辐射域外壁面为无限域组件,流体域进出口面为自由模态管组件,在结构域进出口面设置位移约束,在声场流体域施加声源,以此实现阀门气动噪声的声流固耦合计算。
以2×10-5Pa 作为参考声压,绘制N 模型“A”监测点在频率内的A加权声压级曲线和1/3倍频程图,如图7 所示。声压级曲线呈上下波动状态,但总趋势是随着频率的增加而下降;声压级主要分布在500 Hz~3 000 Hz区间,而又以500 Hz~1 500 Hz为主,“A”监测点的最大声压级99.3 dB(A)对应于频率500 Hz,其次是99.3 dB(A)对应1 313 Hz,处于中低频区域;声压级在高频区呈明显的宽频特性。对频率内的A 加权声压级进行总声压级计算,获得距偏心旋转阀出口和管壁1 米处(“A”监测点)的气动噪声数值模拟值为114.6 dB(A)。
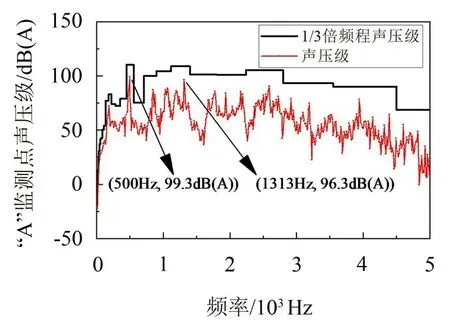
图7 N模型“A”监测点声压级和1/3倍频程声压级曲线
提取最大声压级对应频率500 Hz和1 313 Hz下距阀门出口1米处的360个监测点的声压级,并转换为极坐标的形式,其中Y轴正方向对应极坐标的0°,Z轴正方向对应极坐标的90°,如图8所示。

图8 N模型的最大声压级对应频率下的声指向性曲线
声压级曲线呈中心对称分布,500 Hz 的声压级曲线表现出显著的偶极子声源指向特性,最大声压级位于偏离Z轴45°方向;最小声压级位于偏离Y轴50°方向。1 313 Hz 的声压级曲线表现出显著的四极子声源指向特性,最大声压级分别位于偏离Y轴60°和150°对称轴;最小声压级分别位于偏离Y轴20°和110°对称轴。
提取声场流体域和声辐射域的声压和结构域的位移,采用Actran 软件后处理模块获得500 Hz 和1 313 Hz频率下XZ平面流体域声压云图、声辐射域声压云图和结构域位移云图,如图9 所示。声辐射压力云图和结构域位移云图基本对称;声辐射域的最大声压主要分布于出口管道附近,说明了阀体内腔和出口位置涡旋结构的形成和脱落引起的噪声沿出口管道传播到各处,500 Hz 的声辐射域的声压主要由偶极子产生,1 313 Hz 的声辐射域的声压主要由四极子产生。流体域声压明显高于声辐射域声压,这是由于噪声在穿过阀门和管道结构时产生了传递损失;结构域振动位移变化源自偶极子声源和四极子声源的共同作用。
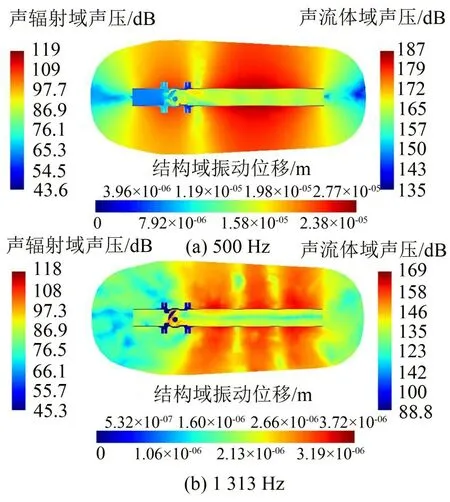
图9 N模型的声压云图和振动位移云图
综上所述,介质为合成气,进口压力为2 MPa(G),出口压力为0.5 MPa(G),开度为40°时偏心旋转阀在“A”监测点的气动噪声模拟值为114.6 dB(A),声压级主要分布在500 Hz~3 000 Hz 区间,并以中低频500 Hz~15 00 Hz 为主,最大声压级对应频率为500 Hz,其次为1 313 Hz。声辐射域的最大声压位于出口管道附近;此数值模型的气动噪声声源包含了介质与阀门和管道内壁的相互作用形成的偶极子声源,以及阀门和管道内涡旋结构形成的四极子声源。
2.3 数值模拟方法验证
Conval 软件是一款专业的阀门选型软件,其气动噪声标准值的算法来源于标准《IEC60534-8-3:2010》[21]。根据第1 节所述偏心旋转阀的结构参数、介质参数和工况参数进行气动噪声标准值计算,结果表明:偏心旋转阀产生的气动噪声处于Ⅳ状态,此时,马赫面形成、分子碰撞减少、激波紊流作用占主要因素;阀门计算流量系数为173.4,开度为40°,出口管道位置马赫数为0.32,节流位置最大马赫数为1.72,管壁外1 米处的A 加权声压级为117 dB(A)。与数值模拟结果比较可知:标准噪声值与气动噪声模拟值误差小于3 dB(A);阀门开度基本一致;出口管道位置处马赫数误差约为8%;节流位置的最大马赫数误差约为2%。基于以上结论判定该数值模拟方法具有可靠性。
3 气动噪声控制机理研究
3.1 阀后加装降噪孔板
在偏心旋转阀与出口管道间位置安装降噪孔板是一种常见的噪声控制方法,该方法基于声路处理法原理,在保持偏心旋转阀原有结构的基础上,降低从声源到监测点的传播声路的声压级[20]。本文对第2节所述N模型的气动噪声进行降噪处理,基于数值模拟阀门开度和边界条件一致性,在阀门出口位置加装厚度为10 mm、线性分布有345 个ϕ5 mm 小孔的降噪板,建立阀后加装降噪孔板后的有限元模型(简称“K 模型”),并按1.3 节网格绘制方法划分网格,在降噪孔板部分进行边界层划分及局部加密处理,流体域网格如图10所示。
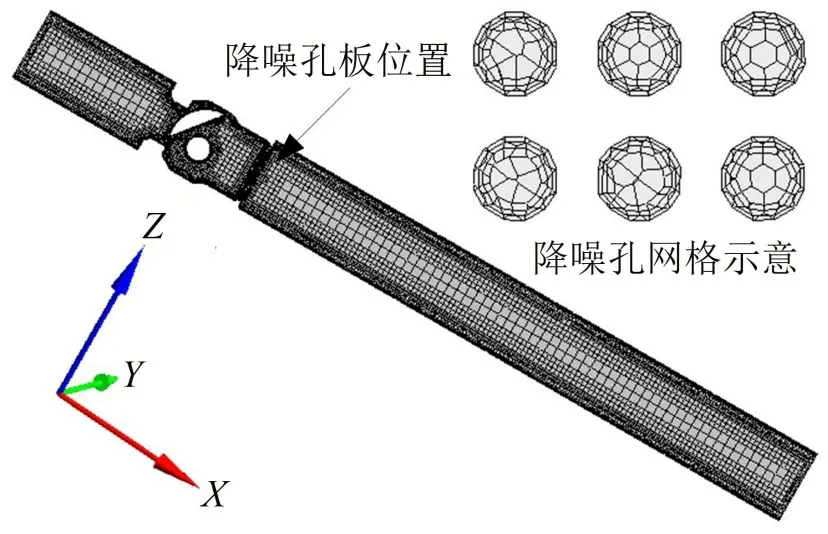
图10 K模型的流体域网格模型
绘制K 模型在0.04 s 时的流线云图和涡量图如图11 所示。比较图6 可知,阀后加装降噪孔板的K模型有效抑制了阀体内腔和出口位置的冲击射流和回流现象,流场的最高流速由526.2 m/s 减小到433 m/s,且最大流速位置转移至降噪孔板出口位置,有效保护了阀体内腔的零部件。K模型的涡旋结构主要分布于阀体内腔和降噪孔板的出口位置。涡旋结构的不断形成和脱落导致的压力脉动作用于阀体内腔和管道内壁,因此产生振动进而导致噪声的产生。
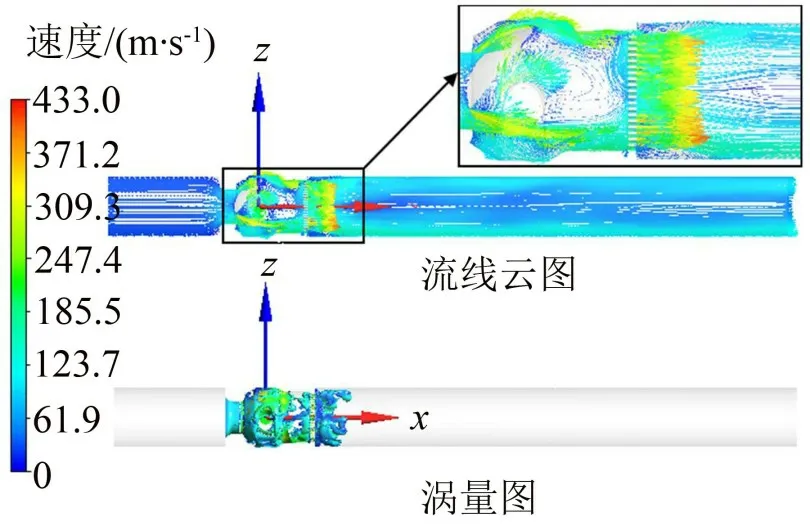
图11 0.04 s时的流线云图和涡量图(K模型)
提取K 模型在采样时间内瞬态流场监测点“B”的压力信息,以及采样频率内监测点“A”的声压信息,对比N模型绘制压力脉动曲线和声压级曲线,如图12所示。采样时间内N模型在监测点“B”位置的最大压差为6.9 kPa(G),K模型的最大压差为3.5 kPa(G)。因此,阀后加装降噪孔板可以通过抑制涡旋结构的形成和脱落,减小压力脉动而控制噪声的产生。采样频率内的声压级曲线均随频率呈整体下降的趋势,最大声压级对应频率由500 Hz转移到1 800 Hz,仍处于中低频区域;K 模型的声压级明显低于N 模型;对频率内的声压级进行总声压级计算,获得“A”监测点的气动噪声模拟值为106 dB(A)。因此,阀后加装降噪孔板通过抑制阀体内腔和出口管道内的涡旋结构的生成和脱落,降低压力脉动强度,从而实现降噪。
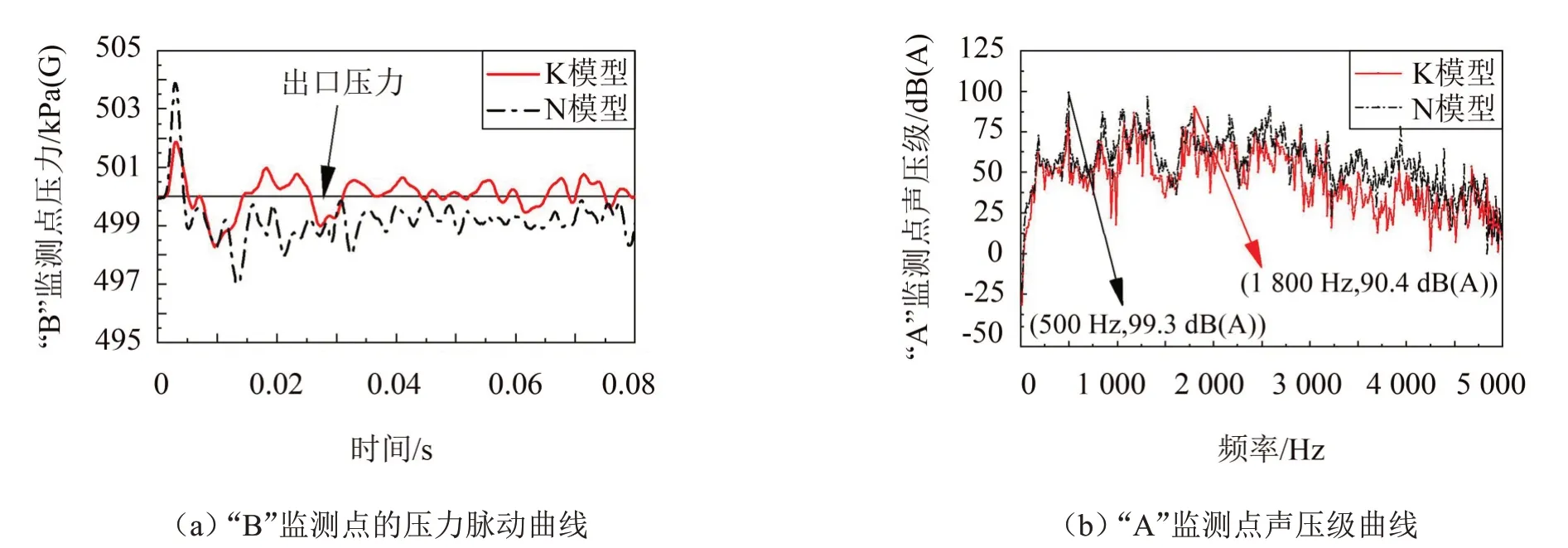
图12 K模型和N模型的压力脉动和声压级对比曲线
3.2 减小流量
以合成气为介质,进口压力为2 MPa(G),出口压力为0.5 MPa(G),以流量为10 kg/s、6 kg/s、2 kg/s 3种工况参数为边界条件,采用多步骤混合数值方法分别建立有限元模型(N 模型、O 模型、P 模型)并开展声流固耦合数值模拟。
提取O模型和P模型在采样时间内瞬态流场监测点“B”的压力信息,以及采样频率内监测点“A”的声压信息,对比N 模型绘制压力脉动曲线和声压级曲线,如图13 所示。N 模型的压力脉动曲线的最大压差为6.9 kPa(G),O 模型为4.8 kPa(G),P 模型为3.28 kPa(G),压力脉动随着流量的减小而降低。3种模型的声压级曲线趋势基本一致,最大声压级对应频率分别为500 Hz、1 325 Hz、1 938 Hz,均处于500 Hz~3 000 Hz 频率的中低频区域,且最大声压级随流量减小而降低。对频率内的声压级进行总声压级计算,获得“A”监测点的气动噪声模拟值分别为102.6 dB(A)和88.1 dB(A)。因此,流量减小后,压力脉动强度变弱,噪声也随之变小。
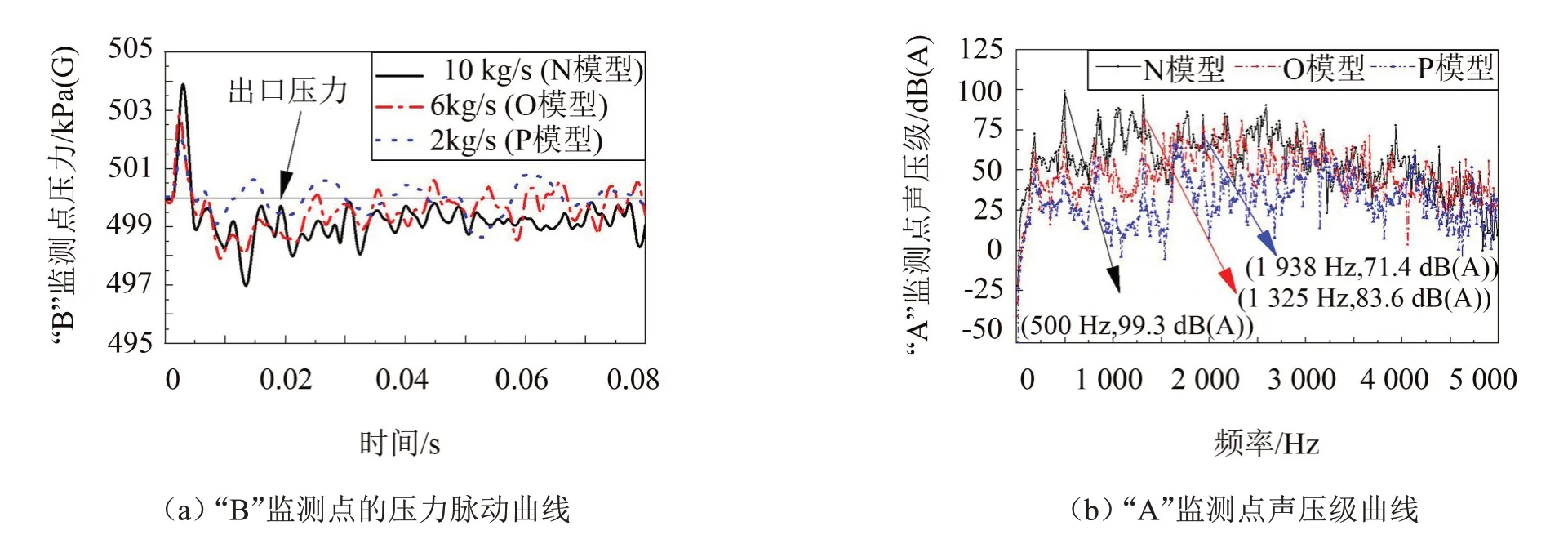
图13 不同流量下的压力脉动和声压级对比曲线
3.3 增大进口压力
以合成气为介质,出口压力为0.5 MPa(G),流量为10 kg/s,以进口压力分别为5 MPa(G)、3 MPa(G)、2 MPa(G)3 种工况参数为边界条件,采用多步骤混合数值方法分别建立有限元模型(L模型、M模型、N模型)并开展声流固耦合数值模拟。
提取L模型和M模型在采样时间内瞬态流场监测点“B”的压力信息,以及采样频率内监测点“A”的声压信息,对比N模型绘制压力脉动曲线和1/3倍频程声压级曲线,如图14 所示。N 模型的压力脉动曲线的最大压差为6.9 kPa(G),M 模型为15.6 kPa(G),L 模型为23.2 kPa(G),压力脉动随着进口压力的增大变强。3种模型的声压级在0~1 500 Hz频率区间无趋势变化,1500 Hz以上的声压级随着进口压力的增大而变大,趋势较明显。对频率内的声压级进行总声压级计算,获得“A”监测点的气动噪声模拟值分别为117.6 dB(A)和119.5 dB(A)。因此,增大进口压力,压力脉动强度变大,噪声也随之变大。
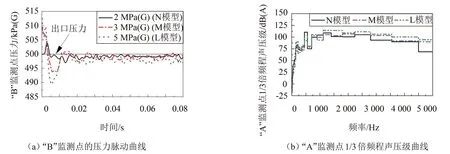
图14 不同进口压力下压力脉动和1/3倍频程声压级曲线
4 结语
本文以煤气化装置中合成气洗涤塔的高压差压力调节用偏心旋转阀为研究对象,根据实际工况参数,采用多步骤混合计算方法开展气动噪声产生及控制机理研究,结论如下:
(1)多步骤混合计算方法基于计算流体动力学CFD 和计算气动声学CAA 提出,应用ANSYS Fluent 计算流体力学软件中的SST-DDES 模型实现瞬态流场的计算,采用Actran 声学软件的Möhring声类比模型、网格映射、傅里叶变换方法实现流场与声场信息转换和噪声求解,获得了管壁外1 米处的气动噪声模拟值,以及瞬态流场和声场结果信息。
(2)介质为合成气,进口压力为2 MPa(G),出口压力为0.5 MPa(G),流量为10 kg/s 时偏心旋转阀在管壁外1米处“A”监测点的气动噪声模拟值为114.6 dB(A),流场和声场结果表明:偏心旋转阀的气动噪声来源于介质与阀门和管道内壁的相互作用形成的偶极子声源,以及阀门和管道内涡旋结构形成的四极子声源共同作用的结果,其声压级频率主要分布在500 Hz~3 kHz 区间。采用Conval 阀门选型软件计算得到的噪声标准值为117 dB(A),两者计算结果误差在±3 dB(A)内,证明了数值模拟方法具有可靠性。
(3)基于阀后加装降噪孔板、减小流量、增大进口压力3 种噪声控制方法进行噪声控制机理研究。研究结果表明:阀后加装降噪孔板削弱了阀体内腔和出口管道冲击波和回流的形成,以及出口管道内涡旋结果的形成和脱落,降低了压力脉动强度,“A”监测点气动噪声降低了9 dB(A);流量减小,降低了“B”监测点压力脉动强度,气动噪声随之减小;增大进口压力加强“B”监测点压力脉动,气动噪声随之增加。
