基于Stewart平台的光电吊舱隔振系统设计

方新文

（中国飞机强度研究所，西安 710065）

光电吊舱是光电侦察装备中的重要组件，也是机载侦察设备的核心部分，广泛应用于陆地、海洋、空中以及空间的侦察。光电吊舱在工作时会受到飞行器速度姿态变化以及发动机振动的影响，振动不仅影响到吊舱设备的使用寿命，还使得吊舱的成像质量严重下降。因此对光电吊舱的振动控制必不可少。光电吊舱的隔振系统的实现方法很多，例如加装不同类型的隔振器或者设计特殊的无转角隔振平台[1]。Stewart平台作为光电吊舱的隔振系统也是一种适宜的实现方法。

Stewart 平台机构是1965 年由美国学者Stewart首次提出并将其作为一种飞行模拟器[2]。平台具有大刚度、高精度和高载荷自重比的特点，适用于高精度、大载荷且对工作空间要求相对较小的场合。目前已经在航空、航天、地下开采、制造装配等行业有着较为广泛的应用。针对Stewart 平台的理论模型与动态力学行为，已有了不少研究。

杨剑锋等[3]设计了一种Stewart平台隔振系统用于某型空间光学载荷的在轨隔振，研究了系统的性能特点，得到了用于六维被动隔振的最佳构型。Lu等[4]研究了一种高静刚度、低动刚度的Stewart平台，实现了6 自由度方向振动的降低；同时基于刚体动力学和非线性弹性理论得到了1阶主振的传递率和功率输出的频响函数。Zheng 等[5]也建立了一种带有Stewart平台的隔振系统，研究了支撑杆的刚度特性，建立了包括几何非线性和刚度非线性在内的非线性动力学模型，并评估了非线性对隔振性能的影响。Wu 等[6]则研究了一种Stewart 平台的理论模型并进行了试验验证，以6 个X 形结构的支撑杆实现了6 个方向的良好性能可调节的隔振系统。Yun等[7]、Yi等[8]、沈慧平等[9]也都基于工程实际设计了不同的Stewart平台并研究了其动态力学性能，取得了不同程度的进展，但是针对被动Stewart隔振平台的解耦隔振设计方法以及等刚度设计方法还少有研究[10－22]。

本文通过建立Stewart平台的理论数学模型，研究被动Stewart 平台隔振系统的解耦设计以及等刚度设计方法。通过有限元仿真以及虚拟试验对设计方法进行验证与分析对比。

1 Stewart平台理论分析

1.1 数学模型的建立及分析

典型的Stewart平台由上安装平台、下安装平台以及平台之间的阻尼连杆组成。平台与阻尼连杆之间采用柔性铰接，可以相互有限度地自由活动。整个系统通过阻尼连杆的伸缩与变形达到振动隔离的目的。图1 所示为Stewart 平台的数学模型，在上安装平台与设备组成的整体的质心处建立Oxyz笛卡尔坐标系。

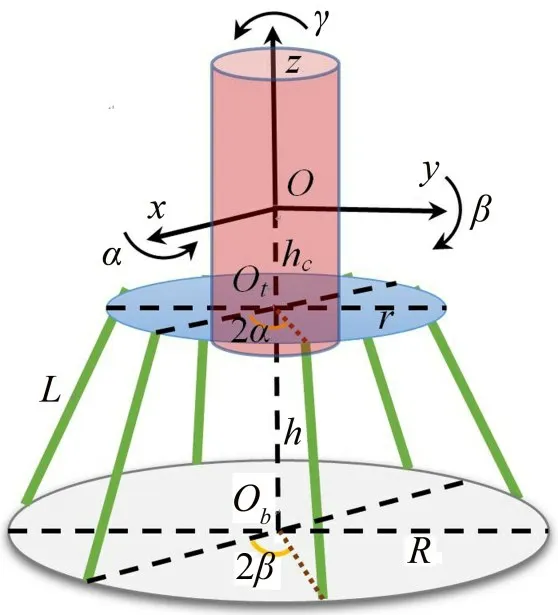
图1 Stewart平台数学模型

图1 中：上安装平台的直径为r；下安装平台的直径为R；上安装平台的圆心为Ot，下安装平台的圆心为Ob；两个平台之间的高度为h；平台之间通过6根支撑杆连接，支撑杆的长度为L；支撑杆连接点与上安装平台之间的夹角为2α；支撑杆连接点与下安装平台之间的夹角为2β；O点与Ot点之间的距离为hc。由以上参数即可以建立起一个Stewart平台。

在微幅振动的条件下，含有基础位移激励的Stewart平台的动力学方程如式（1）所示[23]：

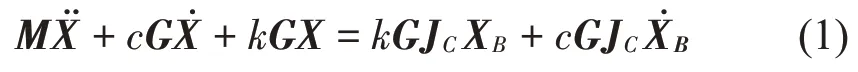
式中：M为上安装平台的质量矩阵；G为Stewart平台的系统构型矩阵，G=JTJ，J为系统Jacobian矩阵；X为上安装平台的位移矩阵；JC为下安装平台到上安装平台的Jacobian 运动传递矩阵；XB为基础位移激励矩阵；c为支撑杆的阻尼；k为支撑杆的刚度。

上安装平台的质量矩阵M，如式(2)所示：

式中：m为包括载荷在内的上安装平台的总质量；I是其惯性张量矩阵，且I=Diag[Ix Iy Iz]。

上安装平台的位移矩阵X，如式(3)所示：

基础位移激励矩阵XXB如式(4)所示：

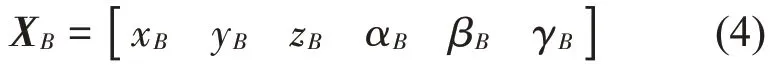
Stewart平台的Jacobian矩阵J如式(5)所示：

式中：L为支撑杆的长度，且有：

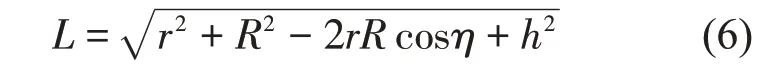
矩阵中其余的参数分别为：

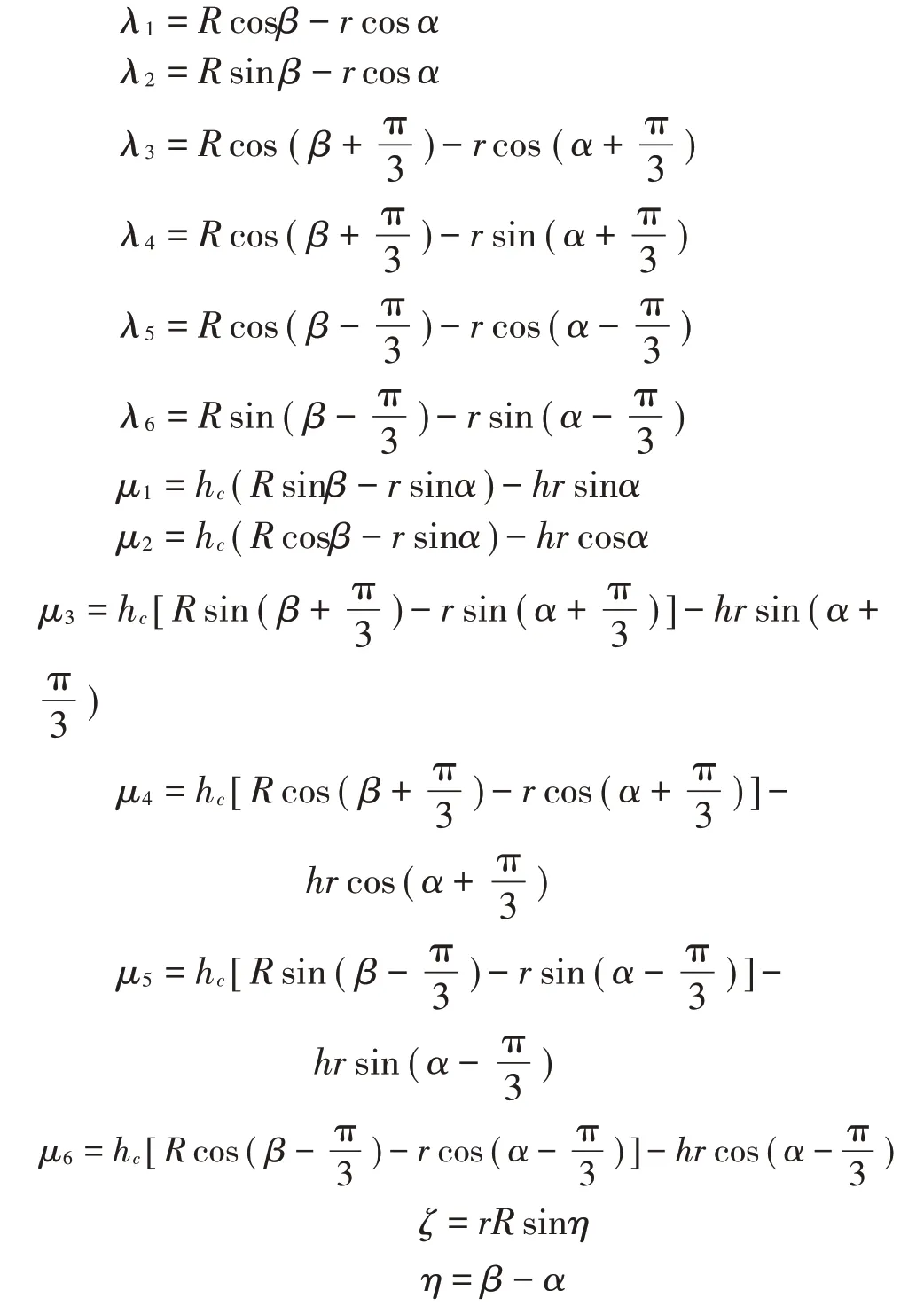
下安装平台到上安装平台的Jacobian运动传递矩阵JC如式(7)所示：

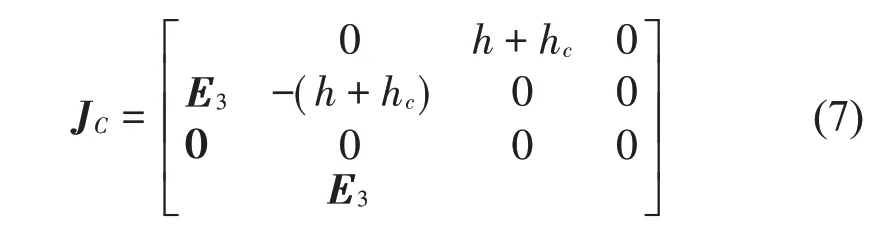
根据系统的Jacobian矩阵J，可以计算得其构型矩阵G矩阵如式(8)所示：

式中各项参数分别为：

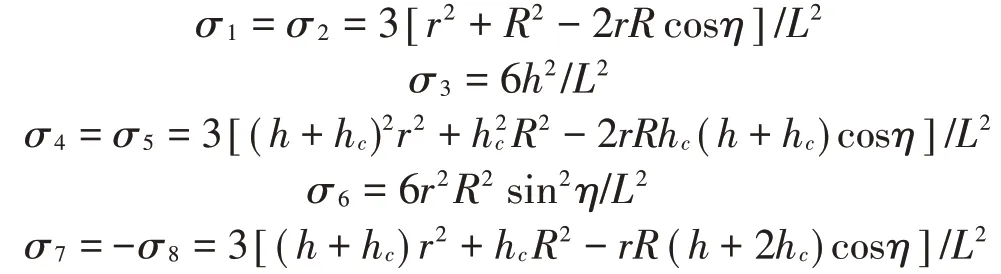
容易看出Stewart平台的动力学方程中，x与β耦合，y与α耦合，z与γ均独立。因此可以将矩阵方程进行分解，得到4个相互独立的动力学方程。

计算得x-β方向耦合动力学方程如式(9)所示；yα方向耦合动力学方程如式(10)所示；z方向动力学方程如式(11)所示；γ方向动力学方程如式(12)所示：

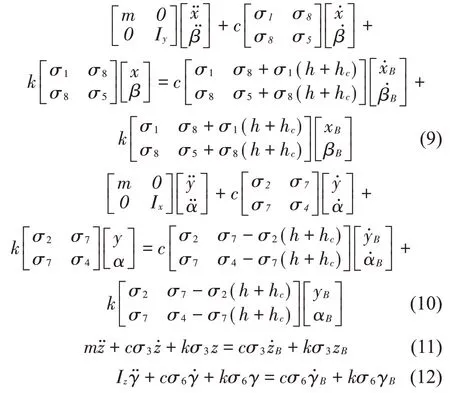
1.2 等刚度解耦设计分析

先考虑一种最简单的情况，即当上下安装平台半径相同，负载的质心位于上下安装平台正中心，并且支撑杆的张角为90°(π/2)时Stewart平台的动力学响应。此时有：

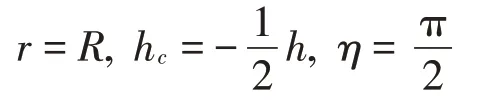
易计算得σ7=σ8=0，在这种安装情况下Stewart平台不会发生耦合振动，各个方向的动力学方程均相互独立。事实上这种结构即为Geng 设计的立方体Stewart 平台[24－26]，其特点是所有支撑杆两两相互垂直，设备质心安装于平台的几何中心处。由此可以保证所有方向完全解耦。当然对于立方体Stewart平台而言，因为必须保证设备的质心在几何中心并且支撑杆两两垂直才能解耦，不仅安装难度较高，占用空间也很大，在很多场合中都难以应用。因此在实际工程应用中还需要考虑其他情况时Stewart 平台的动力学状态分析。

从式(9)及式(10)的耦合方程分析中可以得出：倘若要使平台不发生耦合振动，即各个方向的动力学方程完全解耦，则需要满足：

计算式(9)可以得到系统分别沿x与β方向的模态频率如式(14)所示；计算式(10)可以得到系统分别沿y与α方向的模态频率如式(15)所示：

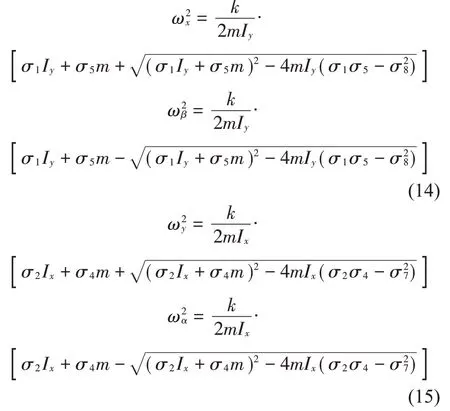
计算式(11)得到沿z方向的模态频率为：

计算式(12)得到沿γ方向的模态频率为：

从计算结果可以看出如果要实现x向与y向等刚度，即x向与y向模态频率相同，则应保证：Ix=Iy，即平台及设备都应该关于z轴对称。由前述分析，为了保证平台不发生耦合振动，应保证σ7=σ8=0，同时为了实现平台在x向与z向等刚度，令ωx=ωz。代入式(14)与式(16)中，则有：

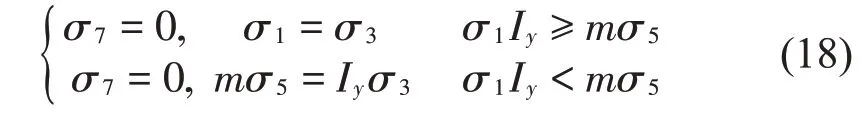
计算式(18)可得：

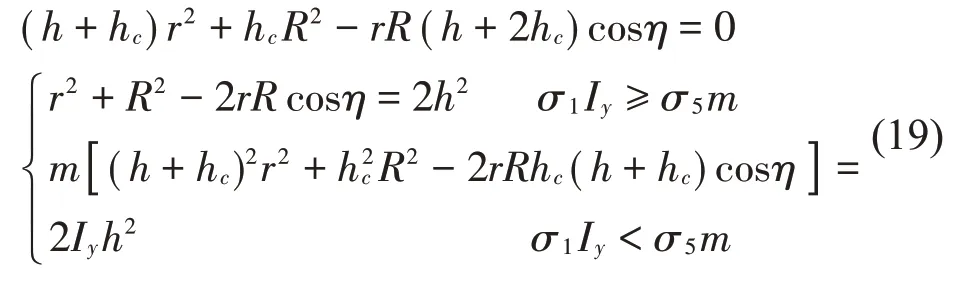
由此得到了各个方向解耦且三向等刚度的Stewart平台设计准则，即在设计时应使Stewart平台的结构参数满足式(19)。

2 Stewart平台设计分析

2.1 隔振系统参数设计

以某型光电吊舱为例研究Stewart 平台参数对整个隔振系统性能的影响。吊舱的质量为9.37 kg，其惯性特性如表1所示。

表1 某型光电吊舱惯性参数

在设计Stewart平台时，一般平台的最大安装直径2R以及安装高度h会因为工程要求受到限制。此吊舱要求最大安装直径不超过0.5 m，安装高度不大于0.1 m，设计R=0.24 m，h=0.1 m。同时设计上下平台的支撑杆安装角度分别为20°与50°。

将这些值代入式(19)中，通过计算可以得到Stewart平台的各项设计参数如表2所示。

表2 Stewart平台设计参数

2.2 隔振系统模态分析

依据计算所得设计参数建立光电吊舱隔振系统有限元分析模型，如图2所示。

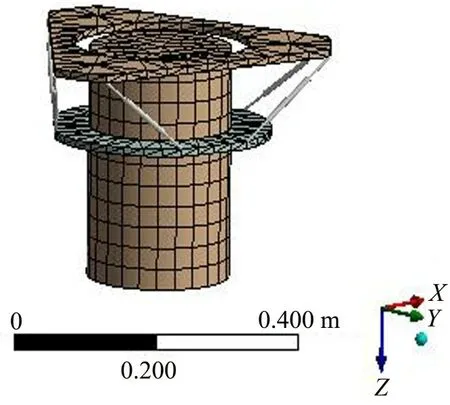
图2 隔振系统有限元分析模型

分别根据式(14)至式(17)计算隔振系统的各个方向的模态频率，并与有限元仿真分析结果进行对比，结果如表3所示。前6阶有限元仿真结果如图3所示。

图3 隔振系统有限元分析结果

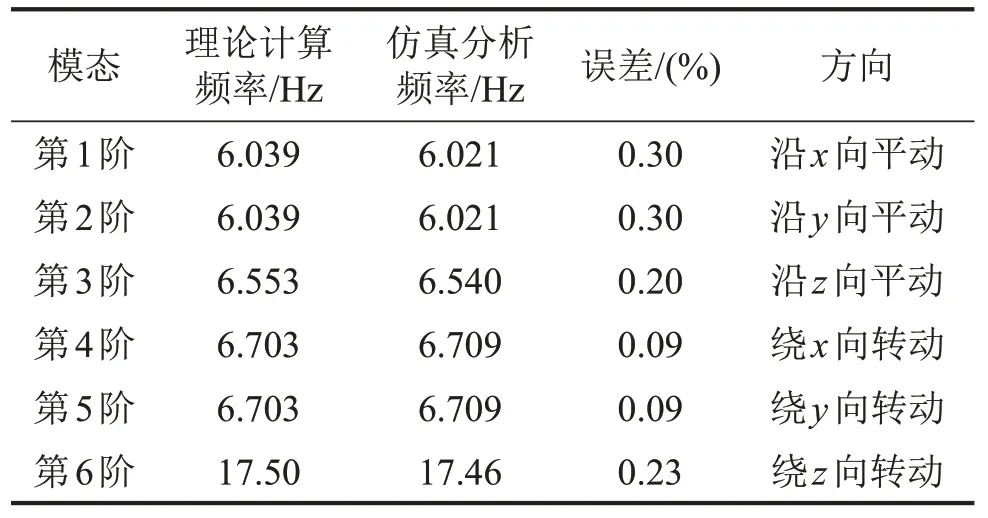
表3 隔振系统设计结果

结果显示理论计算所得模态频率与有限元仿真结果相吻合，二者之间最大误差不超过0.30%.有限元结果显示隔振系统在前6 阶振动均相互独立，没有发生线振动与角振动的耦合现象。同时隔振系统前3 阶模态频率基本一致，实现了三向等刚度设计要求，三轴向的模态频率差别不大于7.8%。

2.3 隔振系统的传递函数分析

在有限元模型的轴向(z)与径向(x、y)分别施加正弦激励，分析隔振系统在各个方向上的传递函数。计算结果如图4所示。

图4 隔振系统传递函数曲线

有限元分析结果显示：隔振系统沿着轴向(z)与径向(x、y)的共振频率接近，基本实现等刚度设计。径向(x、y)已实现解耦设计，传递函数没有角振动(β、α)带来的2阶响应。

3 Simulink仿真分析及验证

3.1 光电吊舱质心对隔振系统的影响

光电吊舱与Stewart平台共同组成隔振系统，吊舱的质心位置对系统的性能有较大影响。系统完全解耦时，即使在共振时线振动也不会引起系统的角振动响应。例如在Simulink 模型中在系统x向施加与x向共振频率相同的定频激励(频率为5.96 Hz，幅值为10 mm)，隔振系统的分析结果如图5所示。

图5 隔振系统正弦响应结果(5.96 Hz,10 mm)

从分析结果可以看出：系统在5.96 Hz处振幅被放大；线振动响应幅值为37.7 mm，放大倍数为3.77倍，同时角振动的幅值不超过1.5×10-5rad。可以认为线振动激励没有引起角振动响应。当进一步调整吊舱的质心位置hc时，计算相应的角振动响应如图6所示。

从图6 可以看出：吊舱的质心位置对隔振系统的解耦影响较大，质心位置改变可以引起较大的角振动响应。如果要使角振动响应小于0.01 Rad(34.4′)，则质心的位置公差不应超过±2 mm。

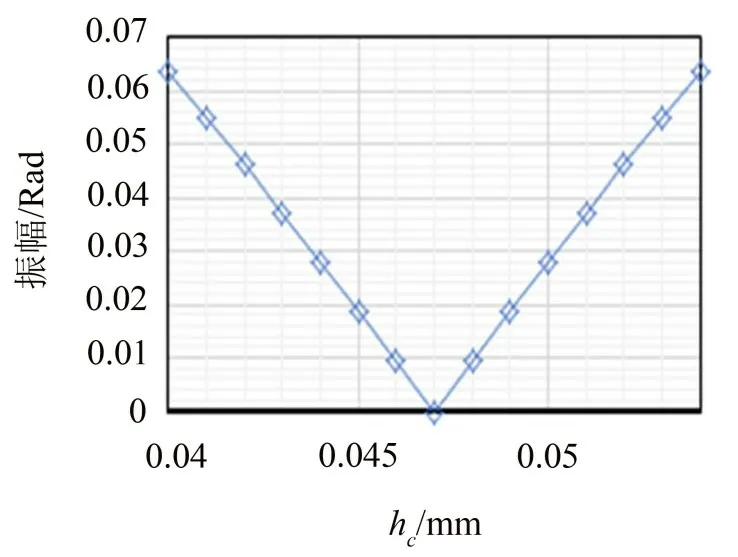
图6 hc对角振动振幅的影响

3.2 白噪声中隔振系统的振动响应

给Simulink 模型施加白噪声随机激励时，计算的结果如图7所示：其中图7(a)为隔振系统径向的振动响应，图7(b)为隔振系统轴向的振动响应。图中的灰色线条为白噪声激励，蓝色线条为线振动响应，红色线条为角振动响应。

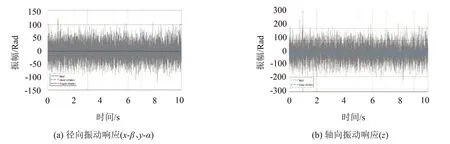
图7 白噪声激励下隔振系统的振动响应

从图中可以看出：系统的角振动响应基本为0，说明系统已经完全解耦，线振动激励不会引起相应的角振动响应。隔振系统性能良好，隔振后系统的振幅已经被很大程度地减弱了，衰减幅度超过78%。

4 结语

通过理论计算研究了Stewart 平台隔振系统的设计方法，采用有限元仿真分析以及虚拟试验对设计方法进行分析对比与验证。

(1)经过等刚度解耦设计之后的隔振系统可以有效地实现3 个方向上模态频率相同且完全解耦。三轴向的模态频率差别不大于7.8%，线振动引起的角振动的幅值不超过1.5×10-5rad。理论模型与仿真分析吻合度很高，验证了模型的工程应用价值。

(2)光电吊舱的质心位置对隔振系统的解耦影响较大，质心位置公差不超过±2 mm 时，耦合产生的角振动响应可以基本满足要求。

(3)所设计的隔振系统性能良好，可以有效地使振动衰减，振动衰减幅度超过78%，研究对光电吊舱隔振系统的设计具有一定的指导意义。由于目前试验条件的限制，隔振系统的性能没有在真实试验中被测试，需要在今后工程实践中进一步验证。