近10年我国民爆物品爆炸事故统计及预测*

张飞燕，张念思，韩 颖，何 鑫

(1.河南理工大学 a.安全科学与工程学院；b.能源科学与工程学院，焦作 454003；2.煤炭安全生产与清洁高效利用省部共建协同创新中心，焦作 454003；3.中原经济区煤层(页岩)气河南省协同创新中心，焦作 454003；4.深井岩层控制与瓦斯抽采国家安监局科技支撑平台，焦作 454003；5.河南省瓦斯地质与瓦斯治理重点实验室——省部共建国家重点实验室培育基地，焦作 454003)

“十四五”时期是推进民爆行业安全、高质量发展的关键时期。民爆行业是推进现代化基础设施体系建设、保障国民经济建设和社会发展的重要基础性行业[1]。随着民爆行业的发展，民爆物品的需求量也快速增大。由于民爆物品本身就具有高危险性，在其生产、运输、贮存和使用等过程都不利于安全管理[2-4]，因此，许多学者针对民爆物品的安全管理进行了研究。高海松等指出我国民爆物品安全管理存在管理模式粗放、缺乏专业技术、安全意识淡薄和监管不到位4大问题[5]；刘治兵认为管理失误是造成民爆物品爆炸事故的直接原因[6]。郑德明从民爆行业市场进行分析[7]，认为民爆物品的流向和使用存在监管盲区，建议有关部门加强管理。民爆物品安全管理问题突显，安全事故时有发生，由民爆物品爆炸事故所带来的人员伤亡和经济损失不容小觑[8,9]。因此，统计我国的民爆物品爆炸死亡事故，科学研判民爆物品安全形式，对预防民爆物品爆炸死亡事故的发生十分重要。

目前，我国许多学者对灾害事故的统计进行了大量研究，主要包括煤矿瓦斯、煤矿水害、粉尘爆炸、交通事故等[10-13]。但是对于民爆物品事故的统计相对较少，不能够直观地看到民爆物品爆炸所带来的危害。基于此，通过中国爆破网和安全管理网，搜集统计了2012—2021年我国发生的民爆物品爆炸死亡事故。从事故发生年份、发生省份、发生环节和死亡人数等进行统计分析，并采用灰色马尔可夫预测模型对未来两年我国的民爆物品爆炸事故起数和死亡人数进行预测，以期加强对于民爆物品的安全管理，有效改善民爆物品爆炸事故频发的局面提供参考。

1 近10年我国民爆物品爆炸事故统计

1.1 基于事故年份的统计

为了保证民爆物品爆炸事故的真实性和准确性，数据全部来源于中国爆破网和安全管理网[14,15]。2012—2021年我国发生了102起民爆物品爆炸伤亡事故，死亡479人。近10年来的民爆物品爆炸死亡事故统计见表1，民爆物品事故伤亡趋势如图1所示。

表 1 2012—2021年民爆物品爆炸事故情况统计表

由图1可以看出：2012年、2014年、2016年我国发生民爆物品爆炸伤亡事故数最多，分别占事故总起数的14.7%；2018年和2021年发生的事故起数最少，分别占事故总起数的5.9%。2012年事故造成的死亡人数最多，死亡90人，占总死亡人数的18.79%；2018年因民爆物品爆炸事故造成的死亡人数最少，占总死亡人数的4.8%。2017—2021年所发生的事故起数相对于2012—2016年的事故起数有所减少，事故造成的死亡人数总体有下降趋势。

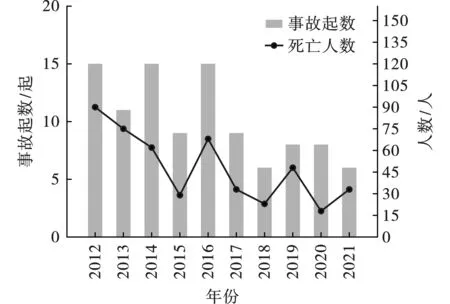
图 1 2012—2021年民爆物品爆炸死亡事故趋势图Fig. 1 Trend chart of civil explosive articles explosion casualties from 2012 to 2021

1.2 基于事故等级的统计

按照我国《生产安全事故报告和调查处理条例》[16]，可将事故等级根据死亡人数划分为特别重大事故(造成30人以上死亡)、重大事故(造成10人以上30人以下死亡)、较大事故(造成3人以上10人以下死亡)、一般事故(造成3人以下死亡)。2012—2021年我国发生特别重大民爆物品爆炸事故1起，2013年的山东保利民爆济南科技有限公司“5·20”特别重大爆炸事故[17]，造成33人死亡，占总死亡人数的6.9%；重大事故15起，占事故总数的14.7%，死亡178人，占总死亡人数的37.2%；一般和较大事故86起，占事故总数的84.3%，死亡268人，占总死亡人数的55.9%。具体情况见表2。

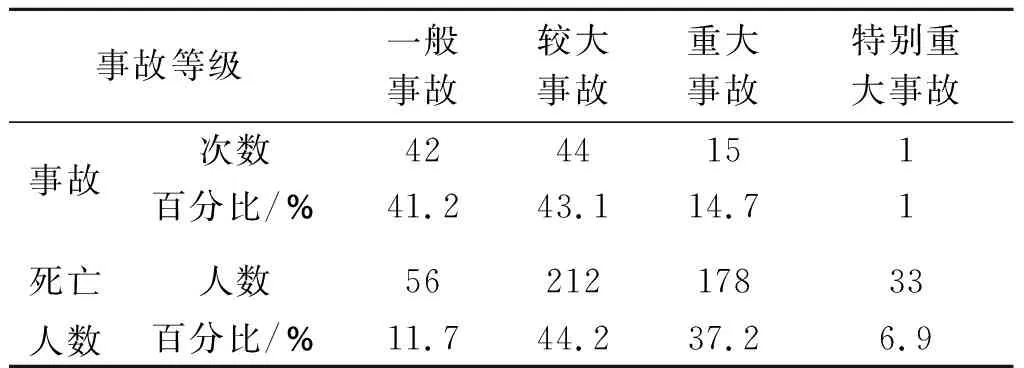
表 2 2012—2021年我国民爆物品爆炸事故等级统计

1.3 基于事故发生区域的统计

2012—2021年我国共有24个省份发生国民爆物品爆炸死亡事故，其中发生民爆物品爆炸死亡事故起数最多的省份为湖南省，发生了17起，造成87人死亡；其次是河北省，发生了11起民爆物品爆炸事故，造成76人死亡；陕西、河南、山西等地也发生多起民爆物品爆炸事故，造成多数人员死亡。具体情况见表3。

表 3 2012—2021年我国民爆物品爆炸事故区域统计

1.4 基于爆炸事故环节的统计

我国民爆行业发展迅速，在民爆物品的生产、运输、贮存和使用等过程爆炸死亡事故时有发生。根据爆炸事故发生的环节对我国2012—2021年的民爆物品爆炸事故进行了统计，见表4，其中生产环节发生的事故起数最多，占事故总数的47.1%，造成的死亡人数为213人，占总死亡人数的44.5%；其次是爆破作业环节，发生了18起爆炸事故，占事故总数的17.6%，造成76人死亡，占总死亡人数的15.8%；贮存环节发生了15起事故，占事故总数的14.7%，造成55人死亡，占总死亡人数的11.5%；销毁环节发生了9起爆炸事故，占事故总数的8.8%，死亡33人，占总死亡人数的6.9%；装卸环节发生了6起爆炸事故，占事故总数的5.9%，死亡64人，占总死亡人数的13.4%；运输环节发生6起爆炸事故，占事故总数的5.9%，死亡38人，占总死亡人数的7.9%。其中，数据统计显示民爆物品的生产和爆破作业环节发生的事故起数相对最多，主要是因为民爆物品生产企业作业环境不安全、管理缺陷等风险因素以及爆破作业单位从业人员专业能力不足[18]、作业现场安全监管不到位而导致爆炸事故发生[19]。

表 4 2012—2021年我国民爆物品爆炸事故环节统计

1.5 基于事故原因的统计

民爆物品发生爆炸产生的冲击波会引起相隔一定距离的炸药爆炸，而爆炸产生的爆炸冲击波又是造成人员伤亡的最主要因素。在此主要把民爆物品爆炸事故原因分为三类：静电/火花、机械作用撞击或摩擦以及违章作业。静电/火花导致爆炸事故是因为在生产过程中机械之间的接触、摩擦使电荷聚集而产生静电火花或者在爆破作业时产生的明火飞溅引燃其他民爆物品而发生爆炸。机械撞击、摩擦导致爆炸事故是因为在民爆物品生产和运输过程中，生产车间机械之间的摩擦、运输过程中民爆物品与车厢之间的撞击摩擦发热，热量积聚导致民爆物品燃烧爆炸。违章作业主要包括在爆破施工时违反国家规定、销毁炸药时操作不当等。对2012—2021年的民爆物品爆炸事故原因进行了统计分析，其中因机械撞击、摩擦而引发的爆炸事故占51%，静电/火花引发的爆炸事故占22.5%，违章作业引发的爆炸事故占26.5%，如图2所示。

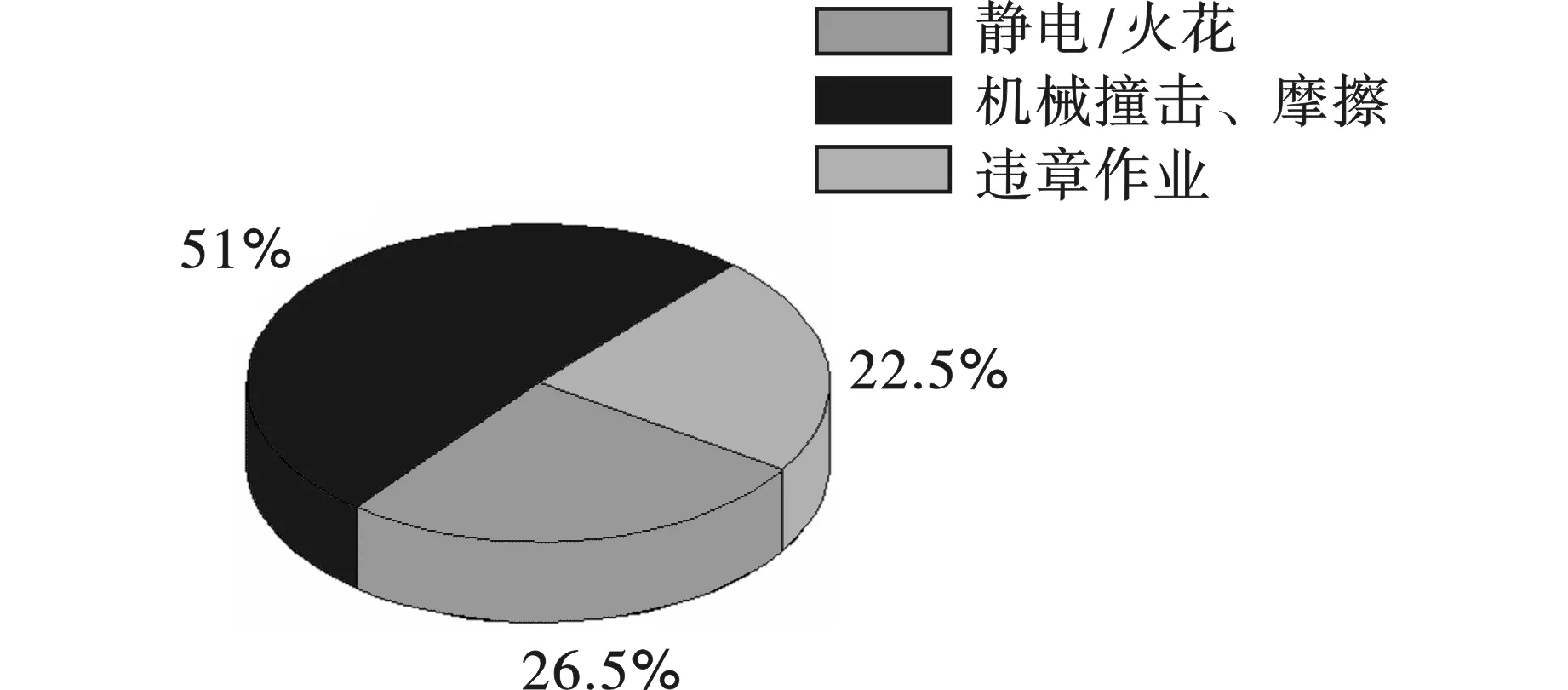
图 2 2012—2021年我国民爆物品爆炸事故原因Fig. 2 Causes of civil explosive articles explosion accident in China in 2012—2021

2 安全措施

加大我国各省份民爆物品的安全监管力度。2012—2021年我国的民爆物品爆炸事故涉及各个省份，其中湖南、河北和陕西三省是民爆物品爆炸事故的主要发生地。各省份民爆物品爆炸事故的发生反映出当地政府对于民爆物品的监管不到位，因此，国家应加大对各省份民爆物品的安全监管力度，落实危险品的安全管理制度。

健全民爆物品生产企业的管理制度，强化生产企业的管理责任。根据数据统计，我国近10年的民爆物品爆炸事故主要发生在民爆物品的生产和爆破作业环节，另外，由于民爆物品具有易燃易爆高危特性不易贮存，也增加了民爆物品爆炸事故发生概率[20]。为了提高民爆物品的安全生产水平，企业必须要健全管理制度，建立具有专业知识水平的安全管理队伍，加强对从事民爆行业人员的专业培训，提高安全管理人员的专业水平，同时加强对民爆物品储存库的监管。

3 事故起数和伤亡人数预测

目前，经过许多学者的研究，出现了大量的预测方法，主要有非线性回归预测、时间序列预测、贝叶斯网络预测、人工神经网络预测等[21-24]。但是，这些预测方法如果想要得到稳定的预测结果，需要有大量的样本数据进行支持[25]，但是民爆物品爆炸事故往往是突然发生的，趋势随机波动且样本数据有限。所以，为了提高预测的精确度，采用灰色马尔可夫预测模型对未来两年的我国民爆物品爆炸事故起数和伤亡人数进行预测。灰色马尔可夫预测模型是灰色模型与马尔可夫模型的结合，融合了这2种模型的优点，比较适用于数据波动大、样本数量小的系统预测[26]，如今在建筑、火灾、危化品、交通等领域的事故预测都有应用[27-30]。

3.1 模型建立

3.1.1 灰色GM(1，1)预测模型

灰色GM(1，1)预测模型基于灰色系统理论[31]，根据事故发展的不规律性，运用累加序列将数据变得具有明显的规律性[32]。

(1)

(2)

称为一阶灰色微分方程，记为GM(1，1)，式中a和u为待辨识参数。

设参数向量

由下式求得最小二乘解

(3)

得到响应方程式为

(4)

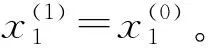
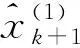
(5)

3.1.2 灰色马尔可夫模型

(1)状态划分

运用灰色GM(1，1)模型得到的民爆物品爆炸事故起数和伤亡人数的预测值，将其与实际值做差得到误差，用误差除以实际值得到相对误差，将序列以相对误差值为标准划分状态，记为E1,E2,L,En。Ei=(φ1,φ2)，其中Ei为系统所处于的第i种状态，φ1,φ2分别为状态区间的上下限。

(2)状态转移概率

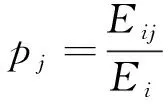
(6)

Eij为状态i到j的一步转移次数，Ei为i状态的数量。根据状态划分的数据，可得到转移概率矩阵为

(7)

式中，p11是指数据从状态1一步转移到1的概率。

(3)预测值的计算

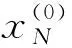
(8)

式中：X(0)为灰色模型预测值；φ1n,φ2n为状态区间的边界值，当大于实际值时取正号，当小于实际值时取负号。

3.2 模型在民爆物品爆炸事故中的应用

以2012—2021年我国民爆物品爆炸事故为原始数据，预测2022和2023年我国民爆物品爆炸事故起数及死亡人数，先通过灰色模型进行预测，然后再对预测结果进行马尔可夫预测优化。2012—2021年我国民爆物品爆炸事故和死亡人数见表1。

3.2.1 事故起数预测

将原始数据x0=[15,11,15,9,15,9,6,8,8,6]代入式(1)～式(4)，得到离散响应方程为

根据式(5)的累减还原，得到民爆物品爆炸事故的预测值，见表5。

根据表1中结果显示，近10年民爆物品事故的灰色预测值与实际值之间的相对误差范围为(-0.50，0.33)，将其划分为3种状态：E1=(-0.50，-0.23)，E2=(-0.23，0.06)，E3=(0.06，0.33)，得到2012—2021年我国民爆物品事故起数各年所处的状态，见表5。

根据各年所处的状态，由式(6)和式(7)可知，一步转移概率矩阵为

由表5可知，2012年的民爆物品爆炸事故起数预测值的状态为E2，则2013年的民爆物品爆炸事故起数的预测值最有可能处于E3状态，故2013年的民爆物品爆炸事故起数为

同理，根据转移矩阵对其他年份的灰色预测值进行修正，并对2022和2023年的民爆物品爆炸事故起数使用灰色马尔可夫模型进行预测，最终得到的修正预测结果见表6。

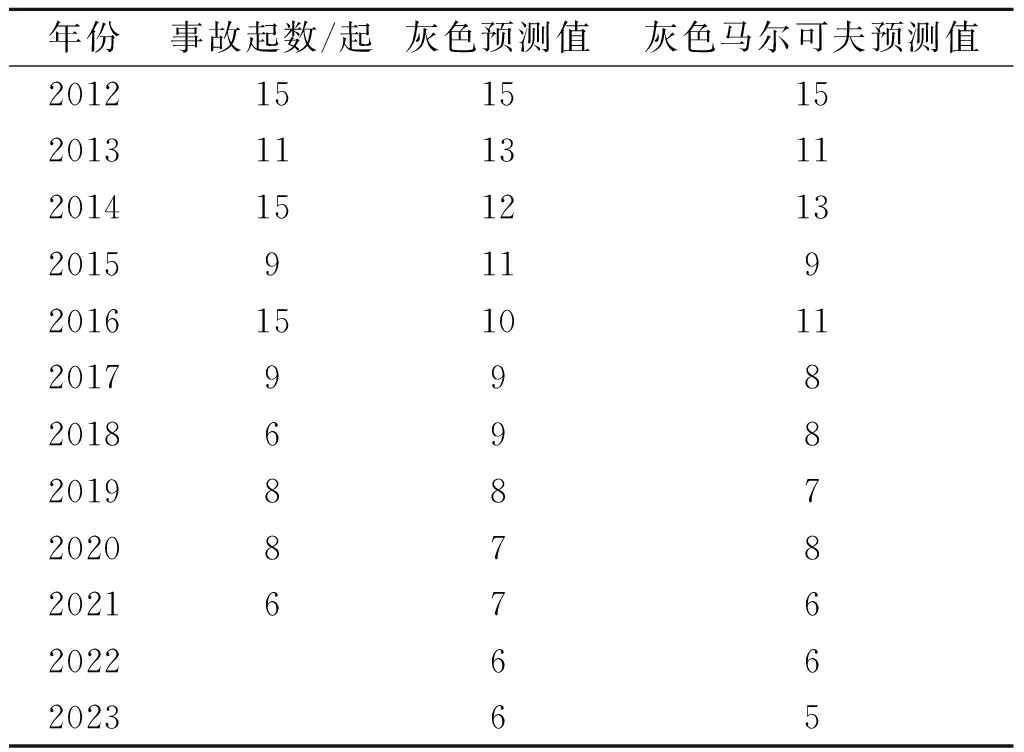
表 6 灰色马尔可夫预测结果

3.2.2 民爆物品爆炸死亡人数预测

将原始数据x0=[90,75,62,29,68,33,23,48,18,33]代入式(1)～式(4)，得到离散响应方程为

根据式(5)的累减还原，得到民爆物品爆炸事故死亡人数的预测值，见表7。

表 7 事故死亡人数灰色预测、相对误差和状态

根据表7中的数据结果显示，近10年民爆物品爆炸死亡人数的灰色预测值与实际值之间的相对误差范围为(-0.83，0.33)，将其划分为3种状态：E1=(-0.83，-0.44)，E2=(-0.44，-0.05)，E3=(-0.05，0.33)，得到2012—2021年我国民爆物品爆炸死亡人数各年所处的状态，见表7。

由式(6)和式(7)可知，一步转移概率矩阵为

由表7可知，2012年的民爆物品爆炸死亡人数预测值的状态为E3，则2013年的民爆物品爆炸死亡人数的预测值最有可能处于E3状态，故2013年的民爆物品爆炸事故起数为

同理，根据转移矩阵对其他年份的灰色预测值进行修正，并对2022和2023年的民爆物品爆炸死亡人数使用灰色马尔可夫模型进行预测，最终得到的修正预测结果见表8。

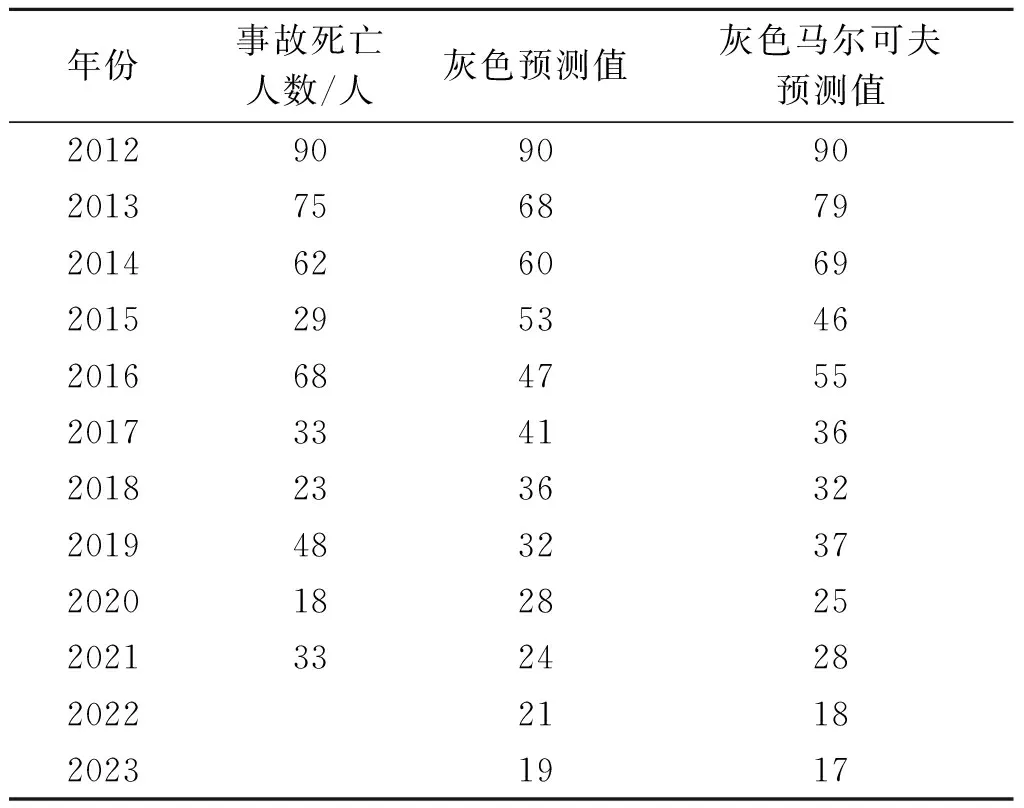
表 8 灰色马尔可夫预测结果

由表6和表8可知，灰色马尔可夫预测值比灰色预测值更接近实际值，所以运用灰色马尔可夫模型来预测2022和2023年的民爆物品爆炸事故起数和死亡人数。2022年我国民爆物品爆炸事故起数预测值为6起，死亡人数为18人；2023年的民爆物品爆炸事故起数预测值为5起，死亡人数为17人。预测结果符合我国民爆物品爆炸事故起数和死亡人数逐渐下降的总体趋势。

4 结论

(1)2012—2021年我国民爆物品爆炸事故起数和死亡人数总体呈下降趋势，安全形式总体比较平稳。

(2)我国民爆物品爆炸事故发生地多在湖南、河北和陕西省份，要因地制宜开展民爆物品的安全管理工作；民爆物品爆炸事故主要发生在民爆物品生产和爆破作业环节；而发生爆炸的主要原因是生产和运输过程中的机械撞击和摩擦，导致热量积聚从而引发爆炸，要强化生产企业的安全管理制度，提高从事民爆行业人员的安全意识。

(3)采用灰色马尔可夫预测模型对2022和2023年的民爆物品爆炸事故起数和死亡人数进行预测，预测2022年我国民爆物品爆炸事故起数为6起，死亡人数为18人；2023年的民爆物品爆炸事故起数预测值为5起，死亡人数为17人。预测结果表明：我国未来两年的民爆物品爆炸事故起数和死亡人数呈下降趋势。但需要说明的是：预测结果的准确度还需时间和事实验证。