基于HJC本构模型的石灰岩冲击破坏形态数值模拟方法研究*

2022-12-19娄乾星陶铁军田兴朝谢财进

爆破 2022年4期

娄乾星，陶铁军，田兴朝，谢财进

(贵州大学土木工程学院，贵阳 550025)

HJC模型是由T J Holmqusit等为解决高应变率及高压荷载下混凝土的大变形问题提出的一种本构模型，目前在岩石材料的动态冲击破坏过程中应用广泛。由于岩石种类不同和地质条件的差异性，该类材料的物理力学性质较难统一。然而，其材料本构模型的参数直接影响数值模拟结果的可靠性，因此对石灰岩材料HJC模型参数的确定和验证是必要的。

目前，国内外学者针对HJC模型参数方面的研究较多，任亮等通过数值模拟和实验分析了HJC模型强度参数A与参考应变率之间的相关性[1]，并对参数进行了优化。米振国等通过ANSYS-LS-DYNA优先软软件研究了适用于130 mm穿甲侵彻混凝土靶的HJC本构模型参数，并以加速度为变量进行了研究[2]。张嘉凡等把HJC本构模型运用到煤岩中，通过数值模拟的方式确定液态CO2爆破效果[3]。刘锦等采用ANSYS/LS-DYNA有限元软件中的HJC本构模型结合实验的方式重现了煤岩的动态压缩的破坏过程[4]。孙玉祥等采用58 mm火炮加载技术和多普勒探针系统测速技术对不同抗压强度的混凝土进行了平板撞击实验的数值模拟[5]，确定了HJC本构模型状态方程参数。汪衡等研究了LS-DYNA软件中HJC本构模型的损伤参数Fs,并通过动能弹侵彻深度和弹体的剩余速度进行了校准[6]。苏伟林等通过HJC本构模型研究了盾构刀具切削混凝土材料时的阻力大小及变化规律[7]。张社荣等结合静动态力学实验确定了HJC本构模型参数[8]。姚本余等通过静力学实验确定了HJC本构模型的基本参数[9]，采用LS-DYNA程序模拟了不同速度冲击煤岩的破碎程度。凌天龙等通过静力学实验与SHPB室内实验确定了砂岩的HJC本构模型的参数[10]，对室内实验与数值模拟的应力-应变曲线进行了对比。李成武等采用LS-DYNA有限元软件对煤岩SHPB实验进行了数值模拟,重现了室内实验过程中的应力波[11]。闻磊等采用HJC本构模型研究了花岗斑岩SHPB动态冲击过程中的力学性能[12]。方秦等通过理论研究确定HJC本构模型参数[13]，采用数值模拟研究了Salem石灰岩的弹体侵彻实验。

目前，HJC本构模型的研究多集中在混凝土冲击破坏方面，也有部分学者将HJC本构模型引入岩石材料的动力学分析中，数值模拟效果较好。但对于我国西南地区常见岩石——石灰岩HJC本构模型参数的研究却鲜有报道，同时在HJC本构模型参数确定方法方面，基本通过传统的室内试验和经验公式确定，不具有适用性及推广性，无法还原石灰岩的SHPB动态冲击破坏过程。

本文以石灰岩静力学试验、三轴围压实验、Hugoniot实验[14]、Hopkinson压杆实验[15]、石灰岩极限面参数A与帽盖模型参数的关系为基础，确定了石灰岩HJC本构模型参数，基于确定的石灰岩模型参数，采用LS-DYNA有限元分析软件再现了石灰岩SHPB冲击破坏的全过程，将该数值模拟岩石破坏过程中的应力-应变曲线与试验进行对比分析，验证该HJC本构模型取值的合理性及有效性，并以动态峰值应力为目标函数，对21个参数进行了敏感性分析，为石灰岩动力学分析提供一种简单可行的数值模拟方法[16-18]。

1 HJC本构模型

HJC本构模型是由T J Holmqusit等为解决高应变率及高压荷载下的大变形问题提出的一种率相关本构模型[19]，适用于拉格朗日与欧拉算法，模型主要包括屈服强度函数、状态方程及损伤演化方程三部分。

屈服强度模型由标准化等效应力表示

(1)

σ*=σ/f′c

(2)

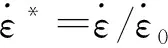
图 1 HJC屈服面方程Fig. 1 HJC yield surface equation

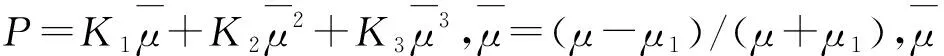
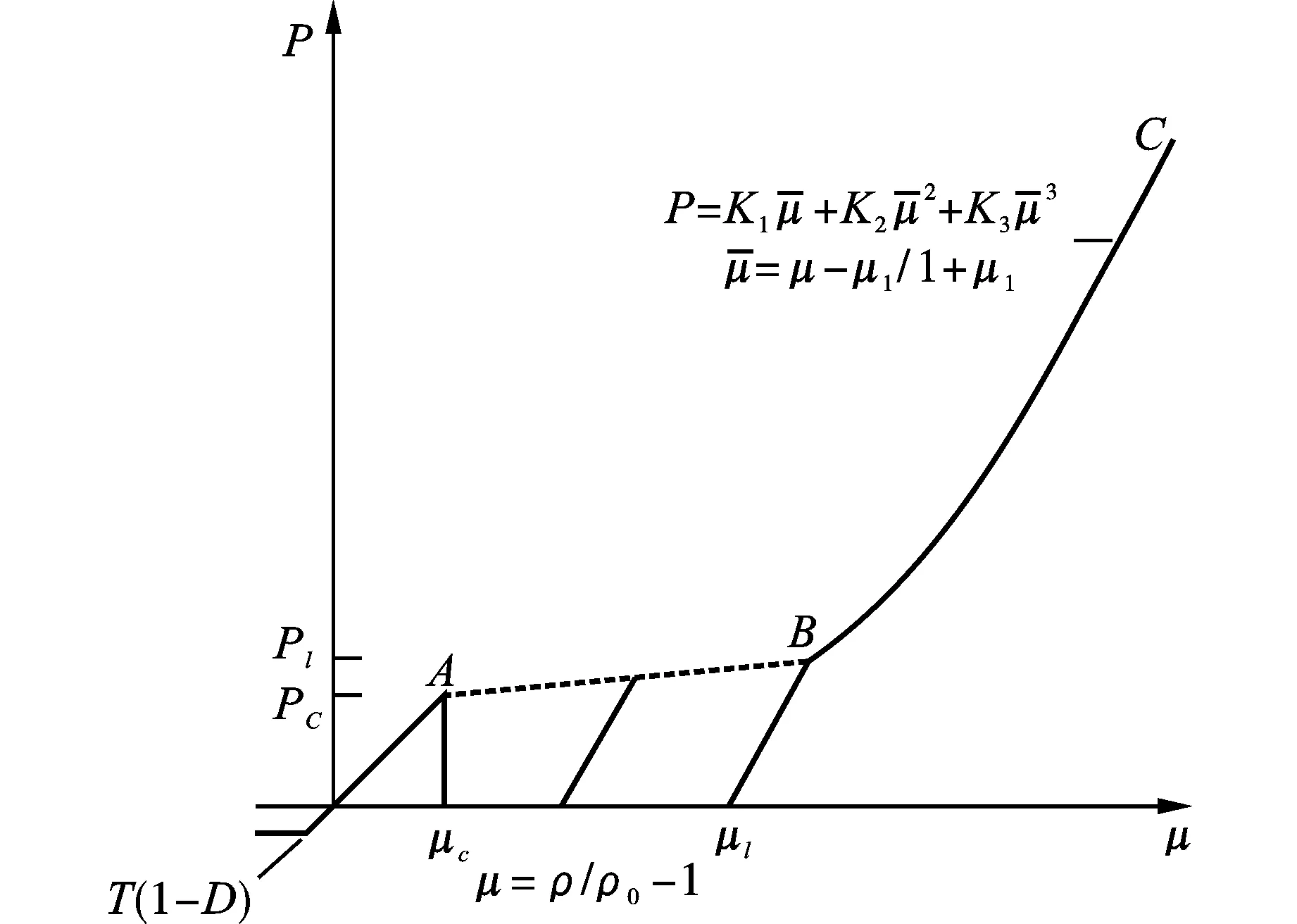
图 2 HJC状态方程Fig. 2 HJC state equation

损伤模型由等效塑性应变和塑性体积应变表征，演化方程为

(3)

(4)

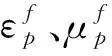
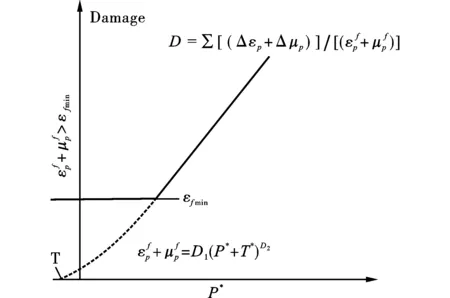
图 3 HJC损伤模型Fig. 3 HJC damage model

2 石灰岩HJC本构模型参数确定

2.1 静力学参数确定

石灰岩试样取自桐梓隧道施工现场，为减小试样的离散型，避免岩石试样组成成分和结构差异对试样结果的影响，所有岩石试样均取自同一岩块。根据国际岩石力学学会(international society for rock mechanics，ISRM)对岩样在力学试样中尺寸的要求[17]，将静力学岩石试样加工打磨制成直径50 mm、高100 mm的标准圆柱体岩样，试件两端面平整度误差不超过0.02 mm，侧面应光滑笔直，满足垂直度要求，如图4所示。

图 4 标准圆柱体岩样Fig. 4 Standard cylindrical rock samples

静力学试验采用中国科学院武汉岩土力学研究所研制的RMT-301岩石与混凝土力学试验系统开展，如图5所示，由静力学试验得到石灰岩试样的静力学参数如表1所示。

图 5 静力学实验Fig. 5 Static experiment

表 1 石灰岩静力学参数

2.2 HJC本构模型参数确定

根据Holmquist等提出的理论[19]，石灰岩的强度大于48 MPa，在不考虑应变率和损伤效应的基础上。

σ*=A+BP*N

(5)

根据帽盖模型与HJC模型的关系式，由方秦等建立的特征化黏性强度参数与帽盖模型参数之间的关系[13]。见图6。

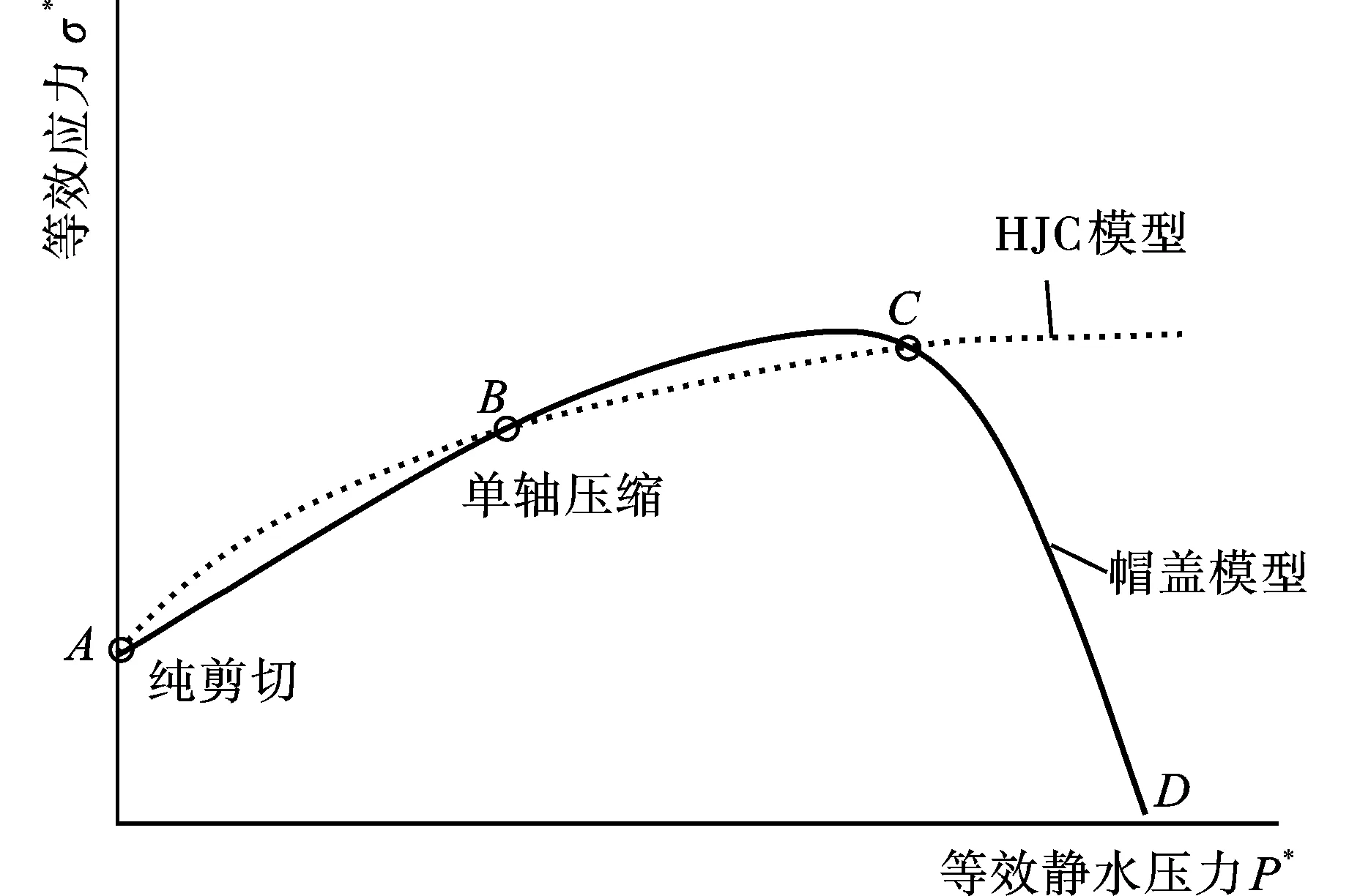
图 6 帽盖模型与HJC模型的关系Fig. 6 The relationship between the cap model and HJC model

AC面剪切破坏面函数为

(6)

CD面帽盖面函数为

(7)

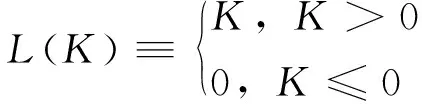
(8)

式中：J1为第一应力不变量；J2为第二应力偏量不变量；α、β、γ、θ、R为材料参数；帽盖面与第一应力不变量J1的交点表达式为

X(k)=k+RFf[L(k)]

(9)

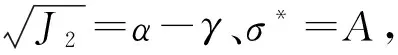
(10)

(11)

根据Fossum等研究的试验数据可得[16]：α=270 MPa,γ=251 MPa，由静力学实验得fC=105.82 MPa，求得A=0.31。

由三轴围压实验数据拟合

(12)

(13)

P*=P/fC=2σ1+σ3/3fC

(14)

根据在不同围压条件下的三轴压缩结果，得到对应的第一主应力σ1，第三主应力σ3，将式(13)、(14)进行归一化，得到每一个相对应的(σ*,P*)，通过公式σ*=0.31+BP*N拟合曲线得到B和N的值，B=1.74、N=0.76，Sm取对应于σ*不再增大时的值，Smax=15 GPa，可以得到HJC模型强度，见图7，表达式为

σ*=0.31+1.74P*0.76

(15)

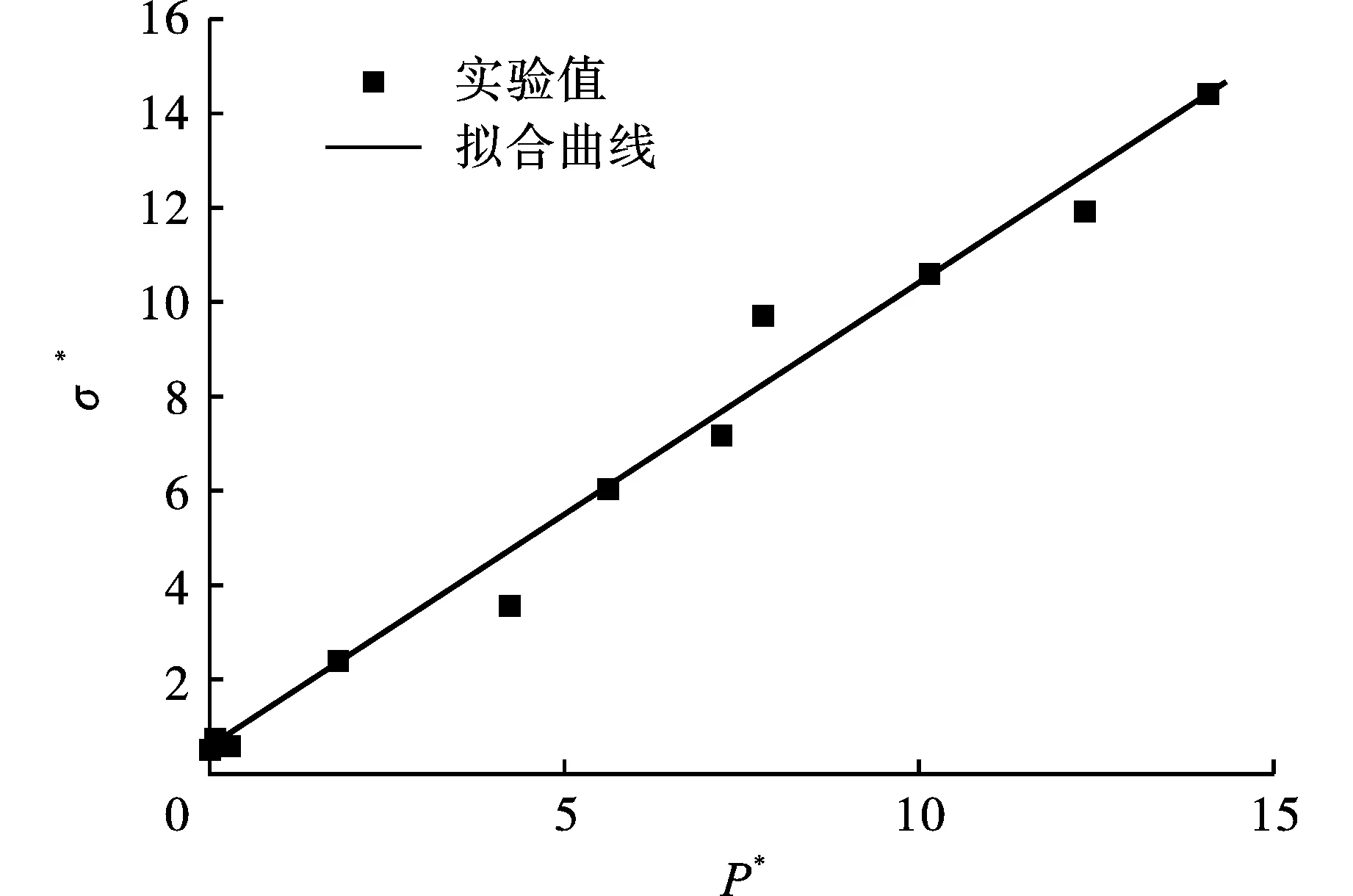
图 7 参数B和N的取值方法Fig. 7 The determination method for the parameter of B and N

体积模量K=PC/μC，岩石的剪切模量G和体积模量K可由下式确定

G=E/[2(1+v)]

(16)

K=E/[3(1-2v)]

(17)

式中：E为弹性模量；v为泊松比，见表1。由公式(16)、(17)求得G=7.65 GPa、K=12.75 GPa。PC、μC为单轴压缩实验测得的静水压力和体积应变，PC=FC/3=0.035 GPa[1]、μC=PC/K=2.7×10-4。μ1=ρ/ρ0-1，ρ为材料的即时密度，ρ0为材料的初始密度，由实验数据得μ1=0.163。

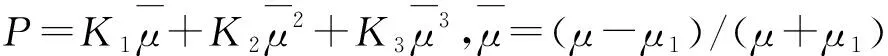
图 8 参数K1、K2、K3取值方法Fig. 8 The determination method for the Parameter of K1,K2,K3

通过SHPB压杆实验，得到了不同应变率下石灰岩单轴动态强度，结合准静态单轴压缩强度，得到不同应变率下的特征化强度σ*，通过拟合应变率与无量纲特征化强度的关系，拟合斜率C=0.017。见图9。

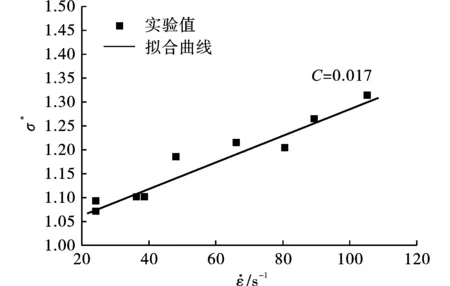
图 9 参数C取值方法Fig. 9 Parameter C value method

Holmquist指出损伤参数与材料强度无关[1]，损伤参数D1根据文献[19]公式D1=0.01/(1/6+T*)=确定，其中T*=T/FC，求得D1=0.045，D2=1、εfmin=0.01。HJC模型参数如表2所示。

表 2 石灰岩HJC模型参数取值

3 参数验证

3.1 模型建立

SHPB动态冲击数值模型的建立采用Hypermesh建立，子弹长度400 mm，入射杆和透射杆长度为2000 mm，子弹、入射杆及透射杆材料模型采用LS-DYNA软件中001号MAT_ELASTIC本构模型，直径均为50 mm，材料模型选择LS-DYNA软件中111号MAT-JOHNSON-HOLMQUIST-CONCRETE本构模型。数值计算模型如图10所示。

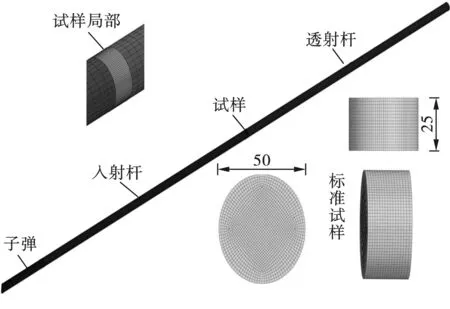
图 10 SHPB数值模拟模型图Fig. 10 SHPB numerical simulation model

采用表2的HJC本构模型参数进行数值模拟计算，为确保岩石计算的精确，对岩石的横向、环线网格均进行了精细化划分，通过在k文件中定义材料、子弹、入射杆、透射杆属性，材料、子弹、入射杆、透射杆均采用面面接触(CONTACT_AUTOMATIC_SURFACE_TO_SURFACE)，在k文件INITIAL_VELOCITY_GENERATION对子弹水平方向添加了和试验对应10 m/s和12 m/s的冲击速度两次冲击入射杆，并在k文件中添加关键字MAT_ADD_EROSION表征岩石的拉伸失效准则。

3.2 SHPB试验

本实验采用阿基米德工业科技有限公司研制的分离式Hopkinson压杆测试系统ALT100进行冲击动力学实验，如图11所示。压杆密度为7.81 g/cm3，弹性模量为210 GPa，泊松比为0.28，纵波波速为5410 m/s，数据采集系统由黏贴在压杆上的应变片、惠斯通桥路(应变片接线桥盒)、超动态应变仪以及高速采集系统组成。

图 11 分离式 Hopkinson 压杆测试系统 ALT100Fig. 11 Split Hopkinson pressure bar test system ALT100

3.3 结果分析

3.3.1 应力-应变曲线

(18)

(19)

(20)

式中：A、L分别为试样的横截面积和长度；E、A0分别为压杆的弹性模量和横截面积;C为压杆的纵波波速。

根据图12可以看出，岩石动态破坏的峰值应力随冲击速度的增大而增大，基于上述确定的参数，10 m/s和 12 m/s的不同速度冲击时，数值模拟得到的应力-应变曲线与室内试验应力-应变曲线都基本吻合，但由于数值模拟默认岩石为各向同性材料，数值模拟得到的曲线为一条光滑的曲线，而实际试验的岩石为各向异性，岩石内部结构的不规整性，岩石破坏过程表现不均匀，导致试验得到的曲线出现凹凸现象。

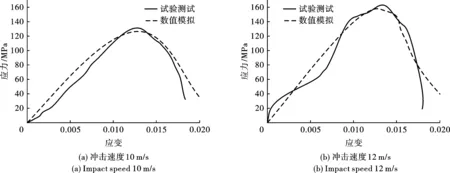
图 12 数值模拟曲线与试验应力应变图Fig. 12 Numerical simulation curves and experimental stress-strain curve

3.3.2 破坏过程

试验过程利用FASTCAM SA1.1型高速摄影仪记录石灰岩在10 m/s速度动态冲击作用下裂纹的扩展过程及最终破坏过程，如图13所示。图14根据相对应10 m/s冲击速度数值模拟得到的裂纹扩展情况及其破坏过程，裂纹的扩展方向大部分沿轴线60°方向，由于应力波在岩石内部多次透射反射，岩石侧面出现拉伸破坏裂纹，并在动态压缩作用下压缩破坏，在拉伸和压缩裂纹共同作用下产生破坏。

根据试验与数值模拟分析可得，数值模拟与SHPB动态冲击试验的应力-应变曲线、破坏模式基本吻合。

4 石灰岩HJC参数敏感性分析

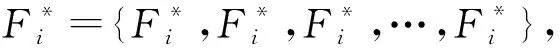
影响冲击后岩石的峰值应力σmax i参数变化率δFij表达式为

(i=1，2，3,…,n；j=1，2，3,…,n)

(21)

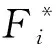
图 13 岩石试验破坏过程Fig. 13 Failure process of rock test

δFij(j=1，2，3，4)对应-40%、-20%、20%、40%。

峰值应力变化δσmax ij表达式为

(i=1，2，3,…,n；j=1，2，3，4)

(22)

式中：σmax ij表示HJC本构模型第i个参数在第j个参数变化率状态下模拟所得的峰值应力。

图 14 岩石数值模拟破坏过程Fig. 14 Numerical simulation failure process of rock

根据在LS/DYNA软件中SHPB数值模拟采用HJC本构模型对21个参数调整所计算的峰值应力变化率结果如图15所示。

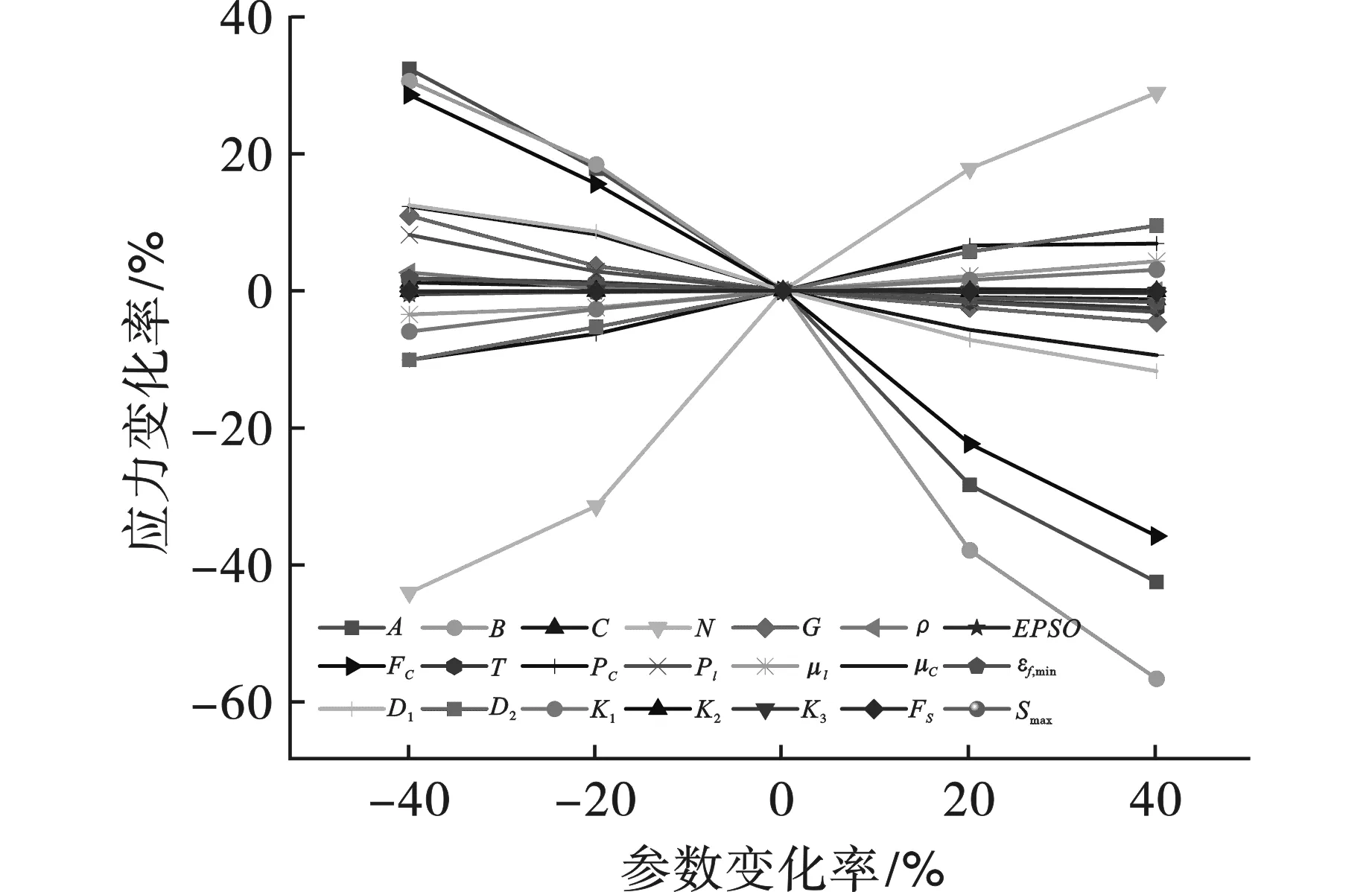
图 15 峰值应力对HJC参数敏感性分析Fig. 15 Sensitivity analysis of peak stress to HJC parameters

由图可得，根据文献[18]，采用剩余峰值应力变化率绝对值|δσmax ij|=10%为参数敏感性分析标准，即岩石峰值应力变化率|δσmax ij|≥10%即认为该参数对峰值应力影响较大，参数A、B、N、FC对峰值应力变化率影响较大，B值的变化使峰值应力变化率接近60%，其他参数对峰值应力变化率在10%之间，说明参数A、B、N、FC对石灰岩破坏时的峰值应力是敏感的。