冰岩耦合体爆炸应力波传播特性分析*
2022-12-19李萍丰王婷婷唐春安张兵兵
李萍丰,王婷婷,唐春安,张兵兵
(1.宏大爆破工程集团有限责任公司,广州 510623;2.东北大学 资源与土木工程学院,沈阳 110819;3.大连理工大学 海岸和近海工程国家重点实验室,大连 116024)
随着西部能源建设兴起,矿产资源开发已逐步延伸至西北地区。岩体中存在着节理、裂隙等缺陷,岩体强度受其影响十分显著[1-3]。在降雨和地下水作用下,裂隙中将会聚集水分,高原寒区特殊地质环境条件诱使裂隙水结冰形成冻结岩体。高寒地区矿产资源开发以及基础设施施工过程中经常会遇到冻结岩体,由于冻结岩体结构的复杂性,其物理力学特性与常规岩石有差异性。而爆破是高寒地区工程项目中较为有效的一种方法。随传播距离扩增,炸药爆炸后所产生的冲击波迅速衰减为应力波,节理、裂隙的存在造成炸药与岩体之间复杂的耦合作用,既削弱了应力波作用,又对岩体破坏模式产生影响,同时爆破效果也发生变化。因此爆破施工过程中应力波在冻结岩体中的传播机制需要深入研究[4-7]。
目前国内外学者针对应力波在节理裂隙中的传播规律从理论[8,9]、试验[10-13]、模拟方面展开研究[14-18]。理论和实验分析不能重现爆炸应力波在节理裂隙中传播全过程,而数值模拟却很好地解决此问题,目前针对应力波传播过程研究主要采用离散元方法UDEC、不连续变形分析方法DDA、连续—非连续单元方法CDEM等。赵坚等将UDEC和Auto-dyna-2D结合[14],分析了爆炸波在非充填节理岩体中传播规律;Zhao等研究了应力波垂直入射线性与非线性节理的传播[15],并与理论解验证UDEC模拟应力波垂直入射节理处传播的可行性。基于UDEC,杨风威等通过计算应力波在含倾斜节理岩体中的传播[16],得出透射、反射系数及波型转换规律。刘婷婷等利用UDEC[17],分析了应力波在平行充填节理岩体中的传播规律,得出节理特性与透射系数之间存在联系;结合DDA程序,张秀丽等计算了应力波在节理裂隙岩体中传播模型[18],得出应力波透射强度随节理数量增加而削弱,反射强度与其相反;运用CDEM,赵安平等研究了节理强度、节理刚度、节理刚度/强度、节理间距、节理倾角等因素扰动爆破效果的规律[1]。
以上相关研究工作主要针对应力波在节理、裂隙岩体中传播特性分析较多,而低温下爆炸应力波在饱冰裂隙岩体传播规律研究略有涉及。鉴于此,笔者针对高寒地区露天矿山爆破开采过程中爆炸应力波传播机制这一科学问题,先界定了冰岩耦合体的定义,探究了应力波在冰岩耦合体中透、反射机制,借助数值实验方式重现了应力波在冰岩耦合体中传播过程,分析了饱冰裂隙及空气裂隙对爆炸应力波传播的影响,并且讨论了爆炸应力波幅值与裂隙冰数量、间距和厚度之间关系,为指导高寒地区露天矿山开采爆破参数设计以及灾害的预防提供理论研究基础。
1 冰岩耦合体定义
广义的冻土泛指温度低于零度且含有冰的岩土体,为冻结土体和冻结岩体的总称。通常所说的冻土是狭义的冻土,仅指冻结土体。而冻结岩体随着寒区基础设施及矿产资源逐步发展,引起人们广泛关注。经过长期地质构造作用,岩体内部孕育了如裂纹、孔洞、节理、弱面以及夹层等缺陷,受低温影响裂隙水将会发生相变成为冰。冻结土体和冻结岩体特性对比如表1所示,二者最大区别是冻结岩体具有各向异性特性,造成外部作用下的响应行为即本构关系有所不同,所以不能将冻土的相关理论直接应用于冻结岩体工程,若仍采用广义冻土的概念易混淆视听。为了更直观体现冻结裂隙岩体的特性,给出了冰岩耦合体的定义。冰岩耦合体意指天然存在或人工形成的岩体、未冻水和裂隙冰的共存体,如图1。

表 1 冻结土体和冻结岩体特性对比

图 1 现场冻结岩体[19]Fig. 1 In-situ frozen rock mass
受高原寒区气候及地质条件影响,露天矿山爆破开采常遇冰岩耦合体区域,爆炸应力波在冰岩耦合体中传播特性与常规岩石存在差异性,因此需要深入探究。
2 冰岩耦合体应力波传播数值模拟
2.1 计算模型建立
为探究应力波在冰岩耦合体中透、反射机制,结合数值模拟手段来重现应力波传播过程。采用RFPA2D-Dynamic建立岩棒模型来讨论应力波在完整基岩、冰岩耦合体、含空气裂隙基岩中传播特性[20],不考虑损伤破坏的影响,因主要研究爆炸应力波在冰岩耦合体中的传播规律,将基岩和裂隙冰假设为均质材料,便于分析。
模型长5 m,高为0.5 m(图2),网格尺寸为1 cm,共计5万单元,节理裂隙厚度为0.05 m,模型右侧为无反射边界,左侧、上下两侧为反射边界,将入射波简化为三角波,在模型左侧施加载荷,幅值为2 MPa(图3),持续时间为1000 μs,单步加载时间为1e-5 s。基岩、冰及空气裂隙参数如表2所示[21]。

图 2 应力波传播数值计算模型Fig. 2 Numerical calculation model of stress wave propagation
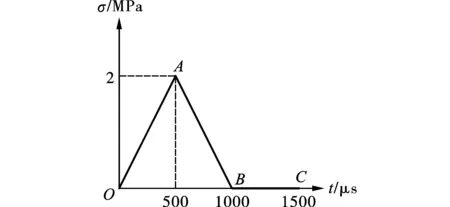
图 3 输入的应力波Fig. 3 Input stress wave

表 2 模型材料参数
2.2 不同裂隙材料应力波传播特性分析
2.2.1 应力波传播形态分析
由图4的应力波传播形态可知:在完整基岩中,应力波在水平方向(X方向)不断向前推进,直至最右端无反射边界逐渐衰减。

图 4 X方向应力波传播形态Fig. 4 Propagation pattern of stress wave in X direction
在含有空气裂隙的基岩中,应力波在近加载端不断推进,在4e-4 s到达空气裂隙处停止向前传播,出现了完全反射,与迎面而来的入射波相撞,应力波符号逐渐发生变化,反向传播至入射端。在含有饱冰裂隙的基岩中,应力波到达裂隙冰处,有部分应力波穿过裂隙冰中继续向前蔓延,形成透射波;另一部分应力波发生在界面处反射,形成反射波,与迎面而来的入射波相撞,应力波符号逐渐发生变化。
数值模拟结果可准确定位应力波传播的具体位置,波峰运移过程可视化,可为工程爆破实施提供一种新的预测方法。
2.2.2 不同测点应力波幅值变化情况
在所建立的模型中取测点A和B来分析应力波幅值随加载时间变化情况。A测点坐标为(1.25,0.25),B测点(3.75,0.25),A测点与B测点之间的距离为2.5 m,计算总时间取2e-3 s。
图5(a)是完整基岩应力波传播情况(X方向),A测点靠近加载端,自3e-4 s受到应力波的影响,5.2e-4 s达到波峰,9.6e-4 s应力波扰动接近尾声;而B测点较加载端远,自8.2e-4 s受到应力波的影响,1.08e-3 s达到波峰,1.32e-3 s结束。A测点应力波幅值为1.946 MPa,B测点应力波幅值为1.828 MPa,衰减系数为0.0472 MPa/m,衰减程度6.1%。右端为无反射边界,应力波在右端逐渐消散殆尽。
图5(b)是含有空气裂隙模型应力波传播情况(X方向),A测点位于空气裂隙左侧,在计算时间2e-3 s内(总计算为200步),X方向应力波变化呈先上升后下降再上升的循环变化趋势。自1.8e-4 s到 7.5e-4 s应力波逐步穿过A测点,因为输入的加载波形为三角波,应力波呈先上升后下降的趋势,此过程中峰值为1.946 MPa;自7.5e-4 s至1.3e-3 s,入射波逐渐到达空气界面,A测点受到空气裂隙界面反射波作用,应力波幅值逐渐变为-1.816 MPa;自1.3e-3 s至1.83e-3 s,空气裂隙界面反射波到达入射端发生二次反射,二次反射波继续作用于A测点,应力波幅值逐渐变为1.906 MPa。上述过程在后续计算中持续循环,这里不做过多阐述。B测点在空气裂隙右侧,应力波没有通过空气裂隙,计算全过程没有受到应力波扰动。
图5(c)是冰岩耦合体内应力波传播情况(X方向),A测点位于裂隙冰左侧,在计算时间2e-3 s内(总计算为200步),X方向应力波变化呈先上升后下降再小幅度波动的变化趋势,与空气裂隙不同之处在于A测点应力波幅值在第二个循环中大幅下降。自1.8e-4 s到7.5e-4 s应力波逐步穿过A测点,峰值为1.946 MPa;自7.5e-4 s至1.08e-3 s,入射波逐渐到达裂隙冰界面,一部分形成折射波通过裂隙冰,另一部分形成反射波又重新到达A测点,削减了正向应力波的能量,应力波幅值为-0.232 MPa;自1.17e-3 s至1.72e-3 s,裂隙冰界面的反射波到达入射端发生二次反射,二次反射波继续作用于A测点,应力波幅值为0.261 MPa,后续循环此过程。B测点在裂隙冰右侧,主要受到透射波的影响,峰值为1.808 MPa,随着计算过程,右端为无反射边界,应力波在右端逐渐消散殆尽。
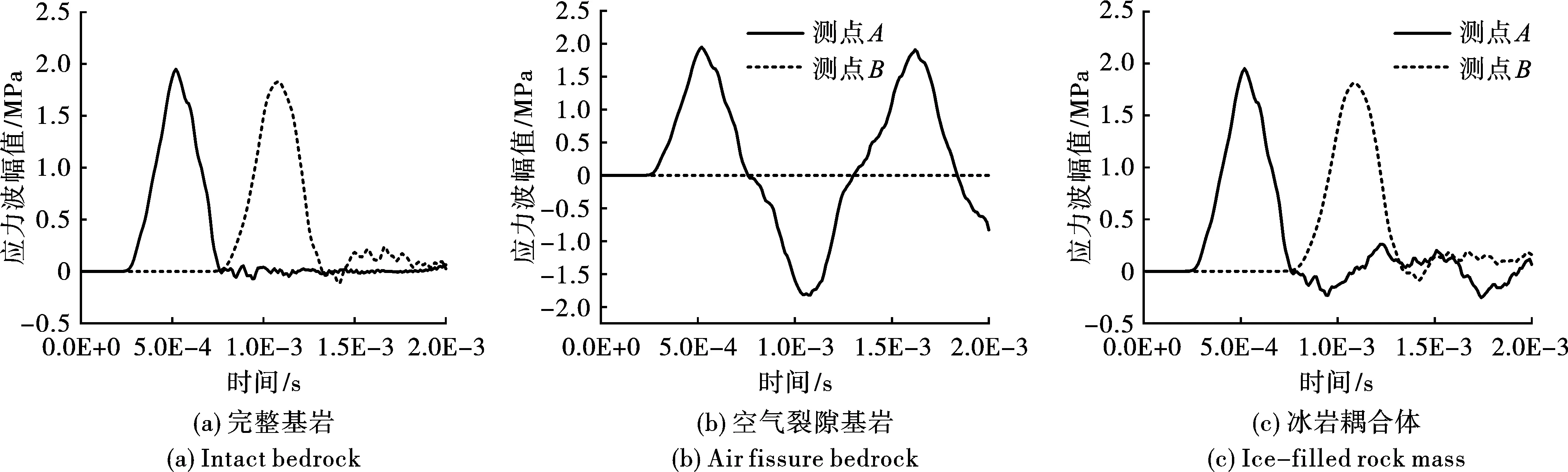
图 5 A测点和B测点应力波变化情况Fig. 5 The variation of stress wave at Point A and B
通过上述分析,可得出与空气裂隙相比,裂隙冰的存在促进了应力波在裂隙岩体中传播,此现象解释了高原岩体爆破施工过程中应力波在冰岩耦合体中传播效果更好,但与完整基岩相比,应力波幅值会有小幅度衰减。
2.3 冰岩耦合体内应力波传播特性影响因素
为了深入探究裂隙冰数量、间距、厚度对应力波传播特性的影响,同样采用图2的岩棒模型来进行影响因素讨论研究,边界条件与加载条件相同,取裂隙冰数量N为1,2,3,4,裂隙冰间距为0.2,0.5,0.8,1.1 m,裂隙冰厚度为0.05,0.1,0.2,0.4 m,同时取应力波衰减程度=(入射波幅值-透射波幅值)/入射波幅值×100%,取应力波透射系数=透射波幅值/入射波幅值。
2.3.1 裂隙冰间距对应力波幅值影响
以裂隙冰厚度为0.05 m,数量为2条为例来分析裂隙冰间距影响,从图6可以看出,应力波在冰岩耦合体中传播,透射应力波幅值都出现了不同程度的衰减,衰减程度维持在7.5%,透射系数维持在0.925。当裂隙冰间距为0.2 m时,A测点于5.2e-4 s达到峰值1.946 MPa,于7.6e-4 s应力波幅值出现负值,其主因受裂隙冰反射波的干扰,后续裂隙冰产生的反射波到达入射端发生二次反射,二次反射波继续作用于A测点,应力值逐渐变为正值,应力波幅值为0.312 MPa,与单裂隙冰作用效果类似;B测点于1.09e-3 s达到峰值1.801 MPa,衰减程度7.5%,透射系数0.925。当裂隙冰间距为0.5 m时,A测点于5.20e-4 s达到峰值1.946 MPa,应力波在后续传播过程中也出现上下波动状态;B测点于1.09e-3 s达到峰值1.802 MPa,衰减程度7.4%,透射系数0.926。当裂隙冰间距为0.8 m时,A测点于5.20e-4 s达到峰值1.946 MPa;B测点于1.09e-3s达到峰值1.792 MPa,衰减程度7.9%,透射系数0.921。当裂隙冰间距为1.1 m时,A测点于5.20e-4 s达到峰值1.939 MPa;B测点于1.09e-3 s达到峰值1.791 MPa,衰减程度7.6%,透射系数0.924。
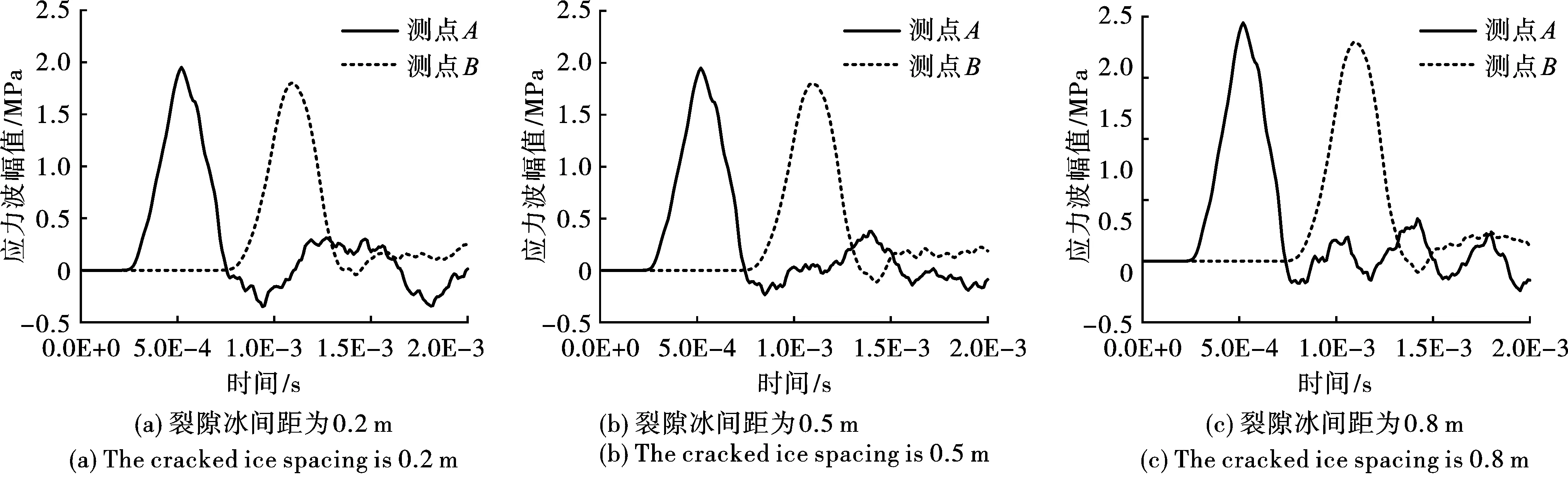
图 6 不同裂隙冰间距A、B测点应力波对比Fig. 6 Comparison of stress wave at Point A and B with different cracked ice spacing
从图7不同裂隙冰间距B测点应力波幅值变化情况可以看出,裂隙冰间距对应力波透射性质影响较小,应力波幅值变化区别不大。

图 7 不同裂隙冰间距B测点应力波幅值Fig. 7 Stress wave amplitude at Point B with different cracked ice spacing
2.3.2 裂隙冰厚度对应力波幅值影响
以裂隙冰数量为1条为例来分析裂隙冰厚度影响,从图5(c)和图8可得出:当裂隙冰厚度为0.05 m时,入射波幅值为1.946 MPa,B测点于1.11e-3 s达到峰值,透射波幅值为1.808 MPa,衰减程度7.1%,透射系数0.929;当裂隙冰厚度为0.1 m时,A测点于5.20e-4 s达到峰值,入射波幅值为1.946 MPa,B测点于1.1e-3 s达到峰值,透射波幅值为1.755 MPa,衰减程度9.8%,透射系数0.902;当裂隙冰厚度为0.2 m时,A测点于5.20e-4 s达到峰值,入射波幅值为1.946 MPa,B测点于1.11e-3 s达到峰值,透射波幅值为1.613 MPa,衰减程度17.1%,透射系数0.829;当裂隙冰厚度为0.4 m时,A测点于5.20e-4 s达到峰值1.946 MPa,B测点于1.12e-3 s达到峰值1.369 MPa,衰减程度29.7%,透射系数0.703。
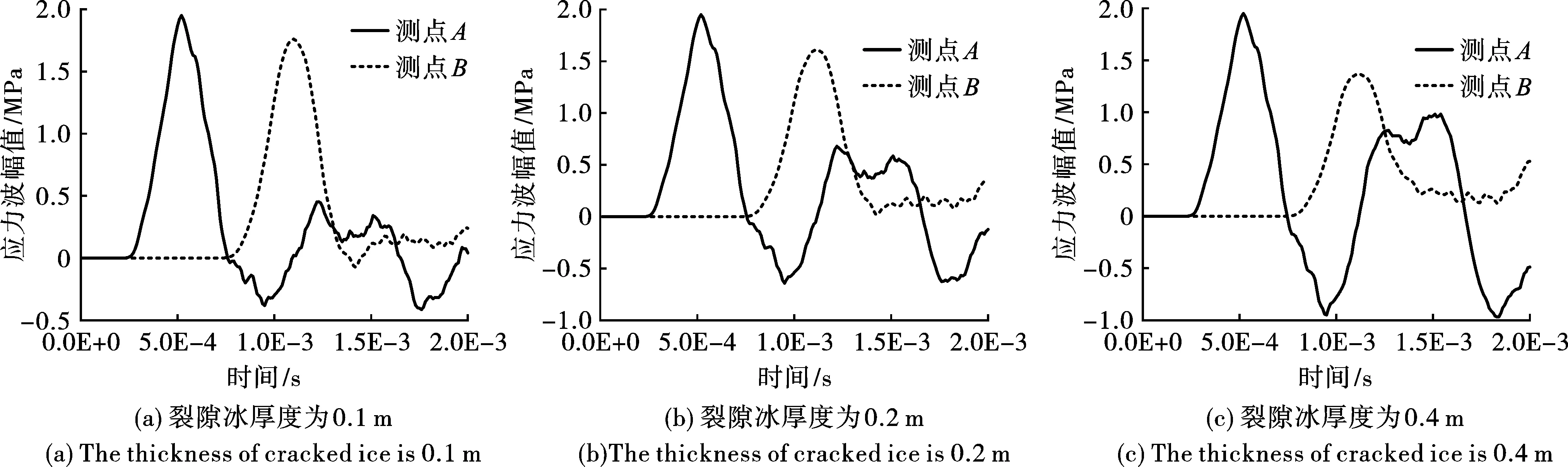
图 8 不同裂隙冰厚度A、B测点应力波对比Fig. 8 Comparison of stress wave at Point A and B with different cracked ice thickness
从图9可得出应力波在不同裂隙冰厚度的冰岩耦合体中传播时,透射应力波幅值出现了大幅度衰减,衰减程度随裂隙冰厚度增加而升高,而透射应力波幅值随裂隙冰数量增加而降低,透射系数也逐渐降低,裂隙冰厚度对应力波透射性质影响较为明显。
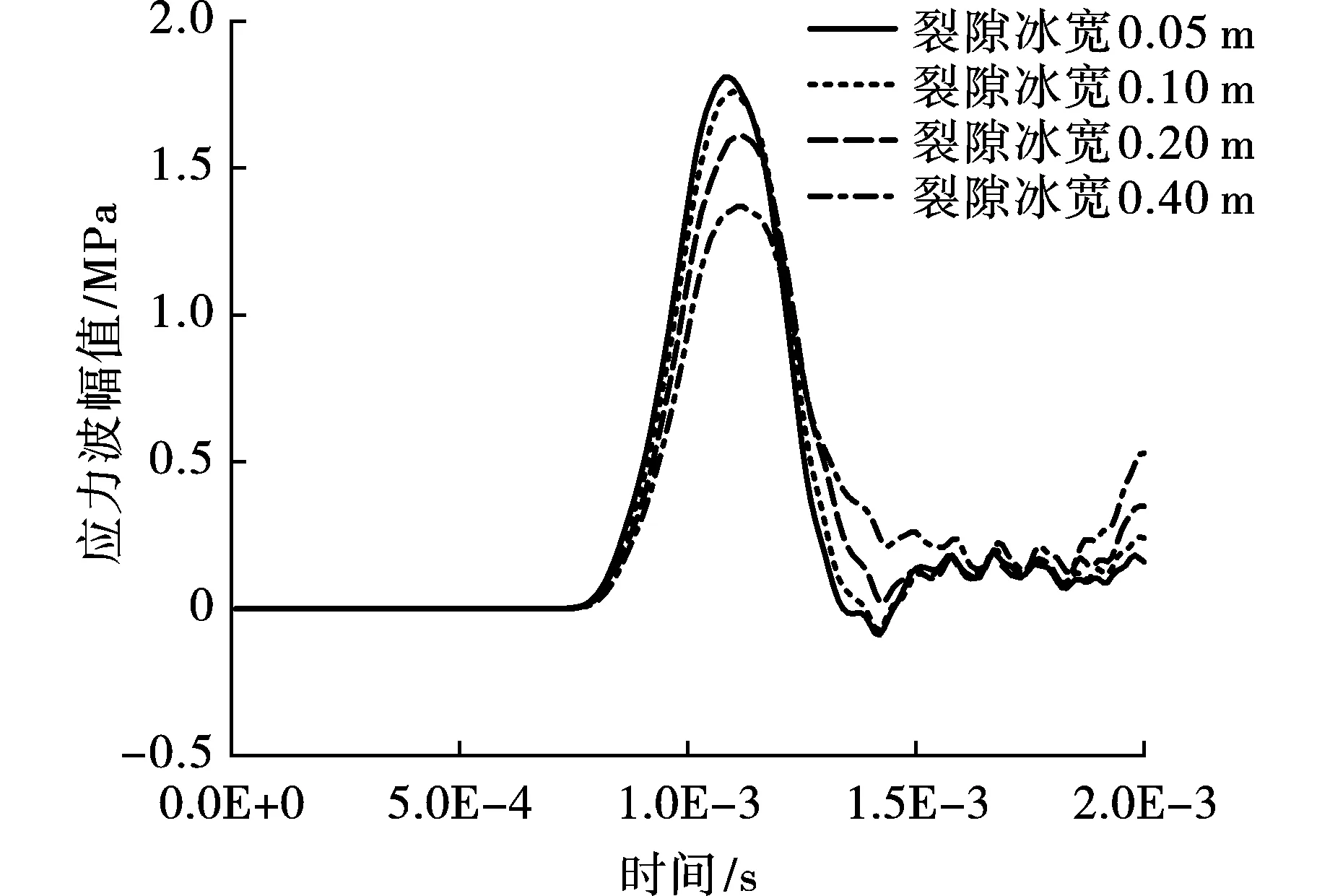
图 9 不同裂隙冰厚度B测点应力波幅值Fig. 9 Stress wave amplitude at Point B with different cracked ice thickness
将应力波衰减程度和裂隙冰厚度进行拟合处理,如图10所示,可得出衰减程度y和裂隙冰厚度x满足:y=0.6527+0.03687x(x取正数)。

图 10 裂隙冰厚度与应力波衰减程度拟合结果Fig. 10 Fitting results of cracked ice thickness and attenuation degree of stress wave
2.3.3 裂隙冰数量对应力波幅值影响
由于考虑裂隙冰数量对应力波幅值影响,分析数据时A测点的选取要避免受到裂隙冰反射波的影响。主要考虑裂隙冰数量为1,2,3,4时透射应力波变化情况,以裂隙冰厚度为0.05 m,间距为0.5 m为例来分析,A测点取值坐标为(0.75,0.25),B测点取值坐标为(4.25,0.25)。
从图11可以看出,当裂隙冰数量为1时,A测点于4.2e-4 s达到峰值,入射波幅值为1.950 MPa;B测点于1.2e-3 s达到峰值,透射波幅值为1.806 MPa,衰减7.4%,透射系数0.926。当裂隙冰数量为2时,A测点于4.2e-4 s达到峰值,入射波幅值为1.950 MPa,B测点于1.21e-3 s透射波幅值为1.800 MPa,衰减7.7%,透射系数0.923。当裂隙冰数量为3时,A测点于5.2e-4 s达到峰值,入射波幅值为1.950 MPa;B测点于1.22e-4 s达到峰值,透射波幅值为1.795 MPa,衰减7.9%,透射系数0.921。当裂隙冰数量为4时,A测点于4.2e-4 s达到峰值,入射波幅值为1.950 MPa,B测点于1.24e-3 s达到峰值,透射波幅值为1.791 MPa,衰减8.2%,透射系数0.918。
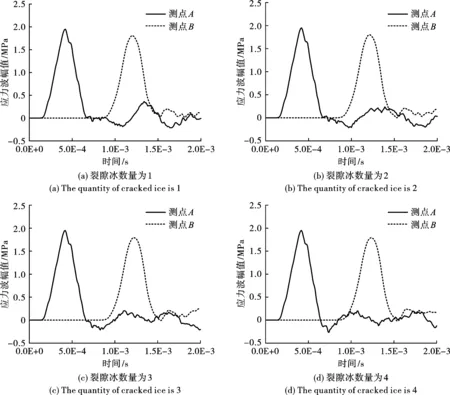
图 11 不同裂隙冰数量A、B测点应力波对比Fig. 11 Comparison of stress wave at Point A and B with different cracked ice quantity
从图12可以看出,应力波在不同裂隙冰数量的冰岩耦合体中传播时,透射应力波幅值都出现不同程度的衰减,应力波衰减程度随裂隙冰数量增加逐渐升高,透射应力波幅值和透射系数随裂隙冰数量增加而逐步降低。
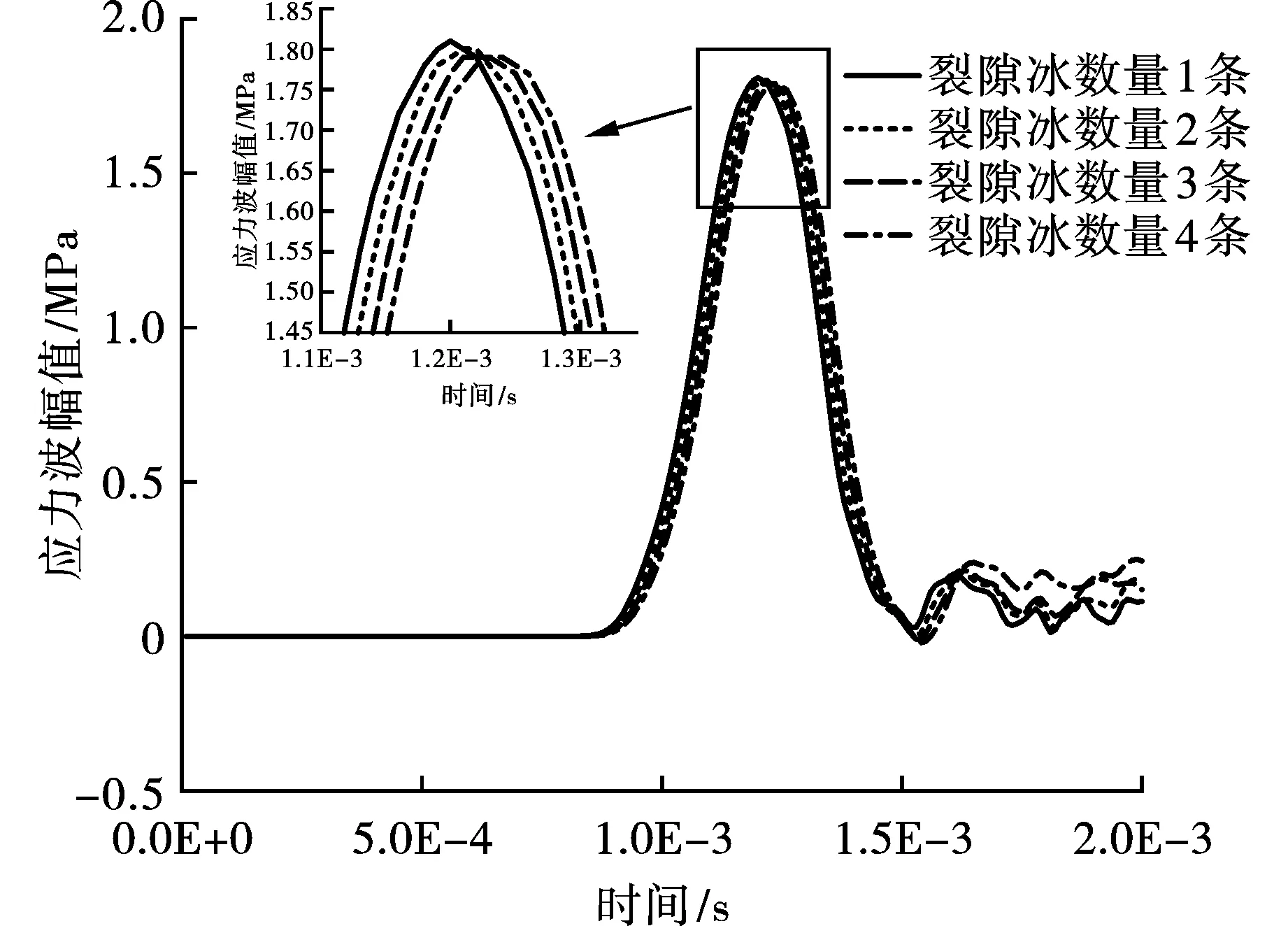
图 12 不同裂隙冰数量B测点应力波幅值Fig. 12 Stress wave amplitude at Point B with different cracked ice quantity
将应力波衰减程度和裂隙冰数量进行拟合处理,如图13所示,可得出衰减程度y和裂隙冰数量x满足:y=0.0715+0.0026x(x取正数)。
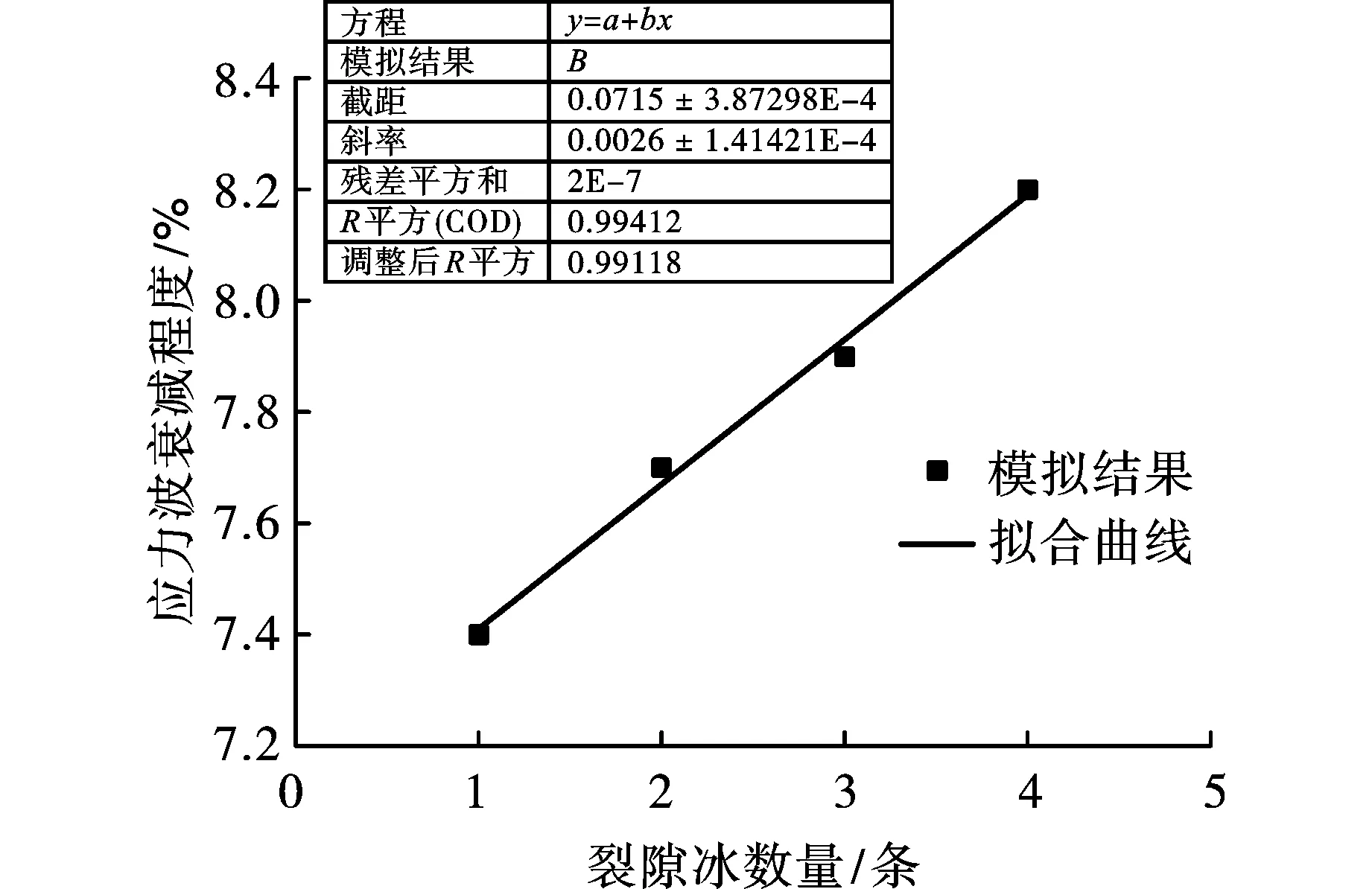
图 13 裂隙冰数量与应力波衰减程度拟合结果Fig. 13 Fitting results of cracked ice quantity and attenuation degree of stress wave
3 结论
(1)与空气裂隙相比,裂隙冰的存在促进应力波在裂隙岩体中传播;与完整基岩相比,裂隙冰的存在削减应力波幅值,应力波衰减程度从6.1%变成7.1%。
(2)若裂隙冰数量、厚度相同,裂隙冰间距对应力波透射效果影响较小,应力波衰减程度稳定在7.5%,透射系数稳定在0.925。
(3)若裂隙冰数量、间距相同,透射应力波幅值及透射系数随裂隙冰厚度增加而逐步降低,而衰减程度逐步升高;应力波衰减程度y与裂隙冰厚度x之间可用函数表示为:y=0.6527+0.03687x(x取正数)。
(4)当裂隙冰间距、厚度相同,透射应力波幅值及衰减程度随裂隙冰数量增加而逐步降低,透射系数也逐步降低;应力波衰减程度y与裂隙冰数量x之间可用函数表示为:y=0.0715+0.0026x(x取正数)。
