家庭医生签约背景下竞争机制引入对医生行为影响的实验研究

李心言

首都医科大学公共卫生学院 北京 100069

1 研究背景

2016年6月，原国务院医改办、国家卫计委等六部门共同发布《关于印发推进家庭医生签约服务指导意见的通知》，提出到2020年力争将签约服务覆盖全人群，鼓励和引导居民就近签约，建立有序竞争机制。目前，我国家庭医生签约覆盖面已得到大幅提升，但国内居民对家庭医生签约认可度不高，获得感不强[1]，引导居民基层就医，有序竞争的机制尚未有效建立。2022年3月，国家卫生健康委等部门联合印发《关于推进家庭医生签约服务高质量发展的指导意见》，明确强化签约服务内涵，健全签约服务激励和保障机制的高质量发展总体思路。如何在增加供给的基础上建立适当的签约服务激励机制，如何建立有效的竞争机制是亟待探索的研究内容。

经济学理论认为竞争会对传统市场产生积极正向的影响，买卖双方拥有完整信息是竞争机制发挥有效作用的假设之一。由于医疗服务市场信息不对称等特点，有关竞争机制发挥作用的理论与实证研究结论存在一定的争议。[2]由于支付方式和全科医生行为的实证研究无法精确测量医疗市场竞争对患者效益的影响[3]，且难以控制医患特征、疾病种类[4]，学者将实验经济学研究方法引入支付方式和竞争机制的研究。

本研究在以往实验研究基础上，结合我国改革实践，优化了实验设计。一是按照绩效分配模式设计竞争场景下的患者分配规则；二是支付方式参数对称式设计下，通过费舍尔组合检验探讨竞争机制与不同支付方式结合是否具有差异；三是以医学生作为主要被试群体；四是通过被试内设计验证不同实验情景转换时医生行为的变化，在大规模实施政策改革之前进行科学评估，为政策实施提供新的理论和证据。

2 研究方法

2.1 实验设计

按项目付费(Fee-For-Service，FFS)是最为常见的医疗服务支付方式。[5]按人头付费(Capitation，CAP)是国外家庭医生签约服务首选的支付方式[6]，国内部分试点地区已探索家庭医生签约服务的CAP模式。[7]本研究选取CAP与FFS两种支付方式，参考Brosig-Koch等[8]、Han设计[9]，以医生竞争辖区内有限患者的方式设计竞争场景，通过实验研究模拟竞争与不同支付方式下的医生决策，分析竞争机制引入的政策效应。

实验采用被试内设计，每名被试只参与一个实验局。实验任务为医学生扮演家庭医生，为两种疾病类型(j)为轻病(x)、重病(z)患者j∈[x,z]，选择提供的服务量qi∈Q=[0, 1, 2, 3, 4……10]。考虑实验顺序效应及控制其影响[10]，每个实验局共分为两部分(表1)，场景1与场景2前、后两部分实验场景完全相同，均为不竞争(No-competition，NC)、竞争(Competition，C)场景，场景3与场景4前、后部分实验场景不同，分别为竞争—不竞争(NC-C)、不竞争—竞争(C-NC)。每部分实验根据场景设定进行15轮，每轮患者的数量和类型保持不变，实验前确定患者顺序，依次为先重、后轻。

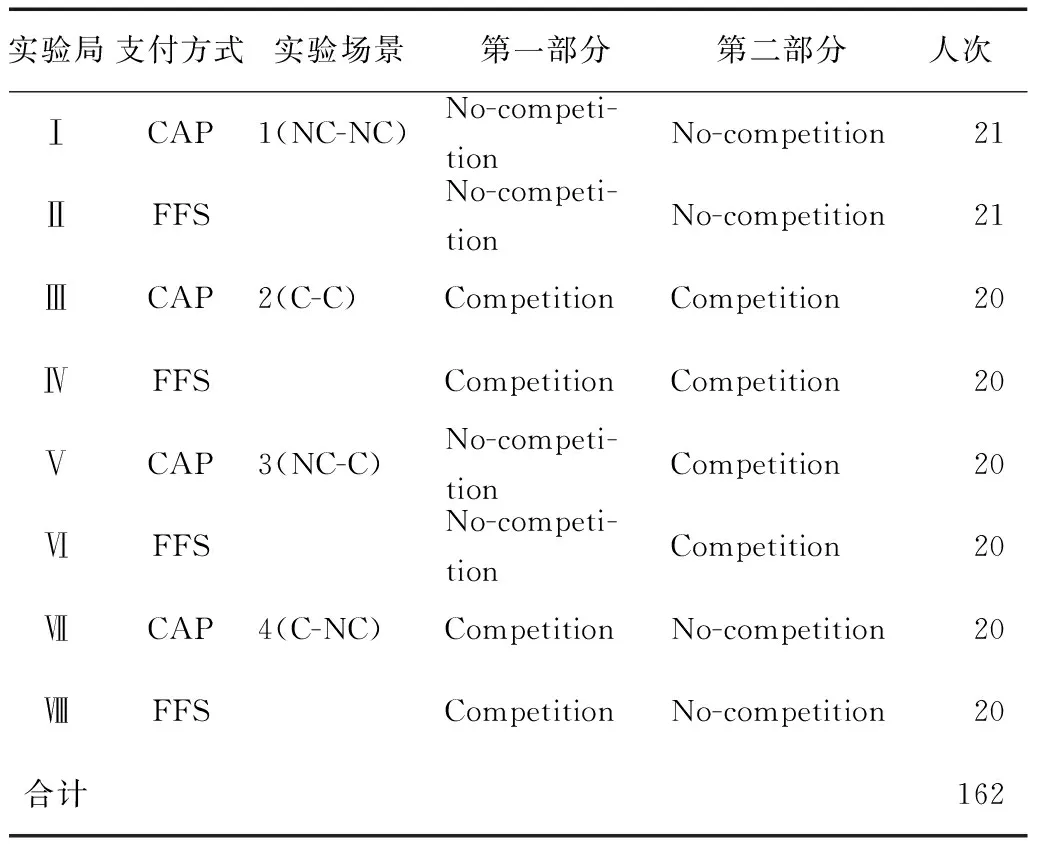
表1 实验局设置

在不竞争场景(NC)，每个医生单独决策，医生决策的服务数量qi，同时决定了医生自身收益π(qi)，及患者健康效益B(qi)。

在竞争场景(C)，两名医生角色(医生1和医生2)同时竞争市场内有限的4名患者，医生1(医生2)各自的决策qi，不仅决定其各自收益π(q1,q2)，患者健康效益B(q1,q2)，而且决定患者数量n(q1,q2)。患者分配规则参考杜学鹏等构建的家庭医生绩效考评机制，根据医生提供服务量所对应的患者健康效益分为五个等级[11]：患者健康效益最大值等级为最优，其余等级按照患者健康效益数值依次递减两个单位，设置为较优、中等、较差、最差。获得较高患者效益等级的医生，将获得4名患者中的3名，另1位医生获得1名；若两名医生提供的患者健康效益等级相同，则各获得2名患者。医生每轮每个决策，提供服务量带来的(总)利润=(单个患者的诊疗费用-成本)*吸引到的患者数量。为了方便被试进行决策，竞争场景两名医生各自提供服务量对应的医生总收益与患者效益矩阵表在实验全程展示。

受试者样本量根据2022年1月预实验数据通过G*power3.1.9.7软件计算确定效应量EffectSizedz=0.9304，每实验局被试人数等于12人(双侧α=0.05)可以使检验效力Power=0.8。在需要交互的实验场景设定双数20人，不需要交互的NC场景设定单数21人进行实验，每实验局被试人数均大于12人满足较高检验效力。实验局Ⅰ、Ⅲ、Ⅴ、Ⅶ为CAP，实验局Ⅱ、Ⅳ、Ⅵ、Ⅷ为FFS(表1)。

2.2 实验参数

2.2.1 医生利润参数

FFS下医生每单位服务量的支付价格p=2。[13]成本参数c的设定采用凸成本函数c(q)=0.1*q2。[14]FFS下医生利润π=pq-c(q)，随着卫生服务数量的增多而增加。CAP下医生支付额R设为固定值10[15]，医生提供的服务数量越少，其收益π=R-c(q)越多。

2.2.2 患者健康效益参数

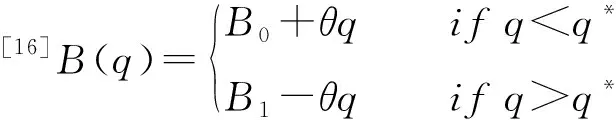
B0为初始的健康效益，疾病严重程度越重，该值越小。θ为患者健康效益函数的斜率，设定θ=1。对于每位患者来说，存在唯一的医疗服务数量q*，即最优服务量使患者健康效益最佳，q*仅受疾病严重程度的影响，疾病严重程度为轻、重的患者分别在医生提供3、7个医疗服务数量时获得其最佳健康效益B1=10。最终两种支付方式下，服务量qi∈Q=[0, 1, 2, 3, 4……10]对应的医生利润以及患者健康效益参数安排如图1。

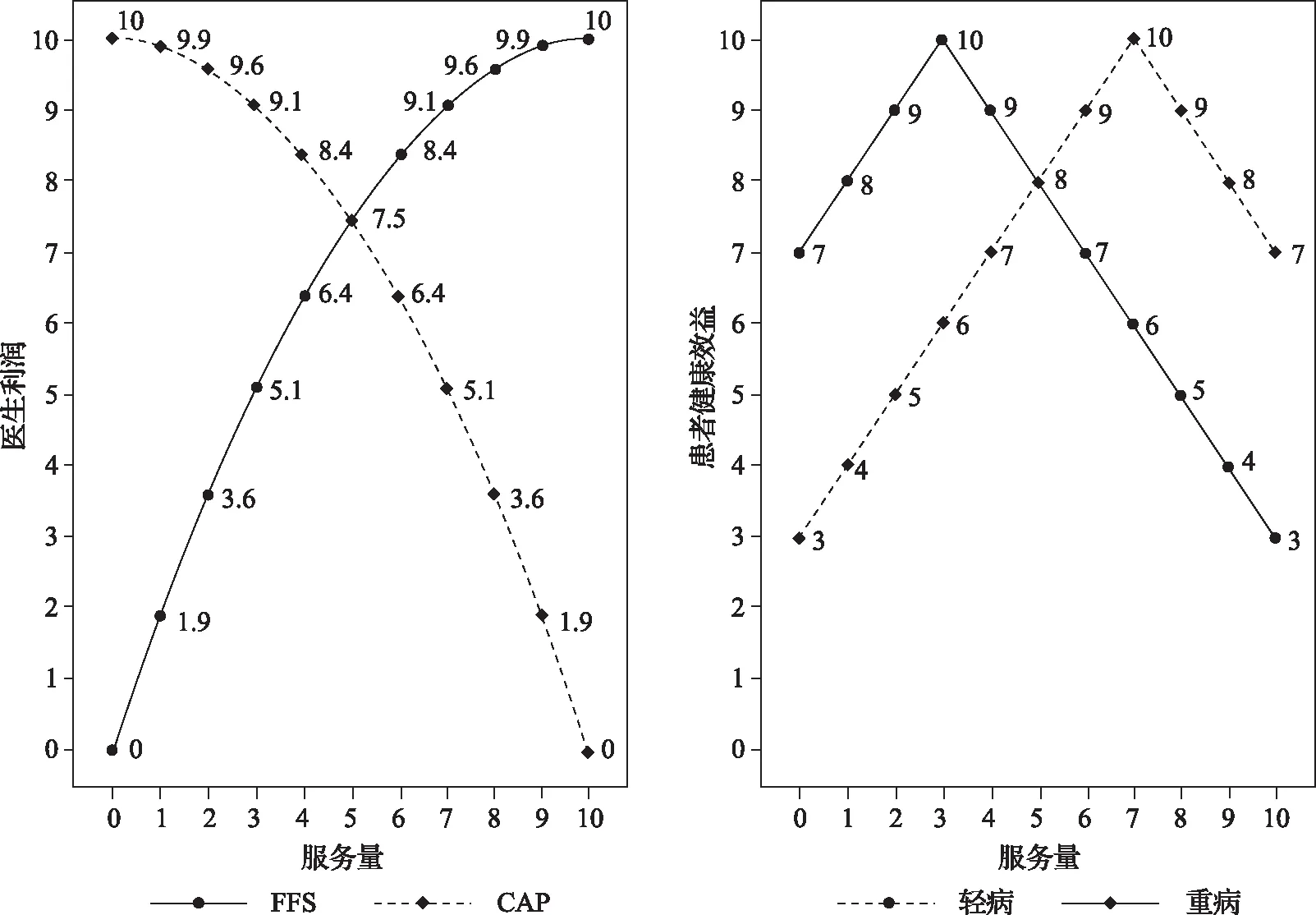
图1 不同支付方式及病情轻重情况下医生利润和患者健康效益

2.3 实验实现与流程

实验采用在线实验形式进行。[17]实验借助“蒲公英”软件实现局域网搭建，实验程序基于预设参数采用Z-tree软件编写[18]，包括主程序Z-tree和子程序Z-leaf。正式实验于2022年5月开展，通过网络宣传形式招募162名医学相关专业三年级及以上本科生和研究生，随机分配到8个实验局。在招募过程中控制本科生与研究生、男性与女性的配额，保证不同教育程度与性别分布均匀。受试者三年级以上本科生85人，研究生77人，男性63人，临床专业105人(判断标准为是否具有规范化培训和执业医师考试资格)，平均年龄23岁。人口统计学特征卡方检验结果显示，受教育程度、性别、是否临床专业、年龄在8个实验局中分布无差异(P>0.312)。

在实验开始前，需要被试提前于个人电脑上，配合下载蒲公英软件与Z-leaf软件。为方便被试操作，需提前录制指导视频、制作操作手册，在实验开始前安排5分钟强制观看指导视频时间。观看完毕，实验员统一测试Z-leaf进入与退出情况，以上操作无误后，为被试发放实验材料，介绍实验任务，被试阅读实验材料并在线签署知情同意书。为保证独立的决策环境，被试不允许相互交流，如有问题示意实验员单独解答。之后，通过先导实验测试被试是否已充分了解实验内容，待所有被试通过先导实验后方可进入正式实验。实验中被试利用个人电脑屏幕上显示的信息进行决策。竞争场景下，首先进入角色分配界面，确认后进入决策界面。两种场景决策完成后，均进入反馈界面。第一部分实验结束后，进入第二部分实验，每部分实验重复15轮，每实验局产生实验记录9 720(15*2*162*2)条。

2.4 实验支付

实验过程中医生决策对应的自身收益π(q)和患者健康效益B(q)，均以实验代币(Taler)表示。为了确保随机分配到任一场景下的受试者拥有相同的平均收益，参考不同市场下区别设置实验代币转换比例的方式。[9]通过预实验发现竞争场景下代币转换比例约为不竞争场景下的2倍水平，最终设定不竞争场景1代币=0.5人民币、竞争场景1代币=0.9人民币。在实验结束后，随机抽取一轮决策的代币按照比例转化为人民币作为实验报酬。顺利完成实验每名被试获得30元基础费用，外加实验决策产生的实验报酬。医疗决策实验的患者健康效益按照相同比例折算捐赠给中国红十字会。为了确保捐赠的真实性，实验员随机抽取一名被试对捐赠成功的结果进行公示，监督者将获得额外的50元。本研究受试者平均实验报酬为119元，累计捐赠金额为8 919元。

2.5 质量控制

为保证决策的匿名性，研究过程中对被试序号进行随机编码。在参与过程中，反复向被试强调实验需要在一个不被打扰的环境进行，每场实验设置2名监督员。

3 研究结果

考虑排除学习与经验效应的影响[19]，将第一部分实验首轮、第二部分实验末轮分别与其他轮次进行比较。各实验局均未发现首轮效应(first-round effect)与终轮效应(end-game)的影响(P>0.288,双侧Mann-Whitney U检验)。实验场景的随机交叉设计，可以有效控制顺序效应的影响。[20]

3.1 非竞争与竞争场景医疗服务量

3.1.1 医生医疗服务量组间比较

在相同实验场景，相同支付方式下第一部分实验平均医疗服务量差异均不显著(P>0.267，双侧Mann-Whitney U检验)。场景1与场景3不竞争场景，CAP下医生提供的平均服务量为3.26(标准差：2.03)，FFS下为6.55(标准差：2.00)。场景2与场景4竞争场景下，CAP下医生提供的平均服务量为4.86(标准差：2.05)，FFS下为5.14(标准差：2.06)。CAP下提供的服务数量均显著低于FFS下服务量(P<0.001,双侧Mann-Whitney U检验)。

与不竞争场景(场景1与场景3)相比，竞争场景(场景2和场景4)医生提供服务量q与最优服务量q*偏差减小。偏差大于0(小于0)代表服务量供给过度(供给不足)。CAP下，轻病下偏差由-1.13减少到-0.01，重病下偏差由-2.34减少到-0.26(P<0.001,双侧Mann-Whitney U检验)；FFS下，轻病下偏差由2.25减少到0.20，重病下偏差由0.87减少到0.09(P<0.001,双侧Mann-Whitney U检验)(图2)。

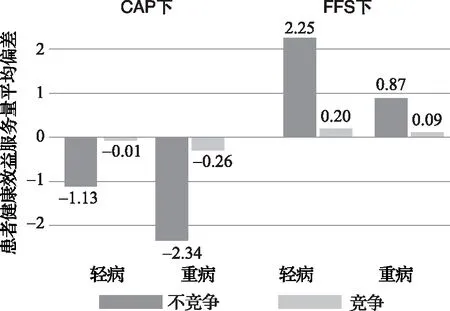
图2 第一部分实验患者健康效益最优服务量平均偏差

第二部分实验与第一部分实验趋势相近，在相同实验场景，相同支付方式下平均医疗服务量差异均不显著(P>0.315，双侧Mann-Whitney U检验)。与不竞争场景(场景1与场景4)相比，竞争场景(场景2和场景3)两种支付方式医生提供服务量与最优服务量偏差均减少(P<0.001,双侧Mann-Whitney U检验)。

3.1.2 医生医疗服务量组内比较

将第二部分与第一部分实验数据组内比较显示，场景1NC-NC(P>0.673,双侧Wilcoxon signed-rank检验)、场景2C-C(P>0.250，双侧Wilcoxon signed-rank检验)，平均服务量并未出现差异。

场景3NC-C、场景4C-NC实验场景变换后，两部分服务量组内比较出现显著差异(P<0.021,双侧Wilcoxon signed-rank检验)。场景3和场景4竞争场景相较于不竞争场景，CAP下医生提供的服务数量增加；FFS下医疗服务数量减少(表2)，两种支付方式竞争场景最优服务量偏差均缩小(P<0.001,双侧Wilcoxon signed-rank检验)。

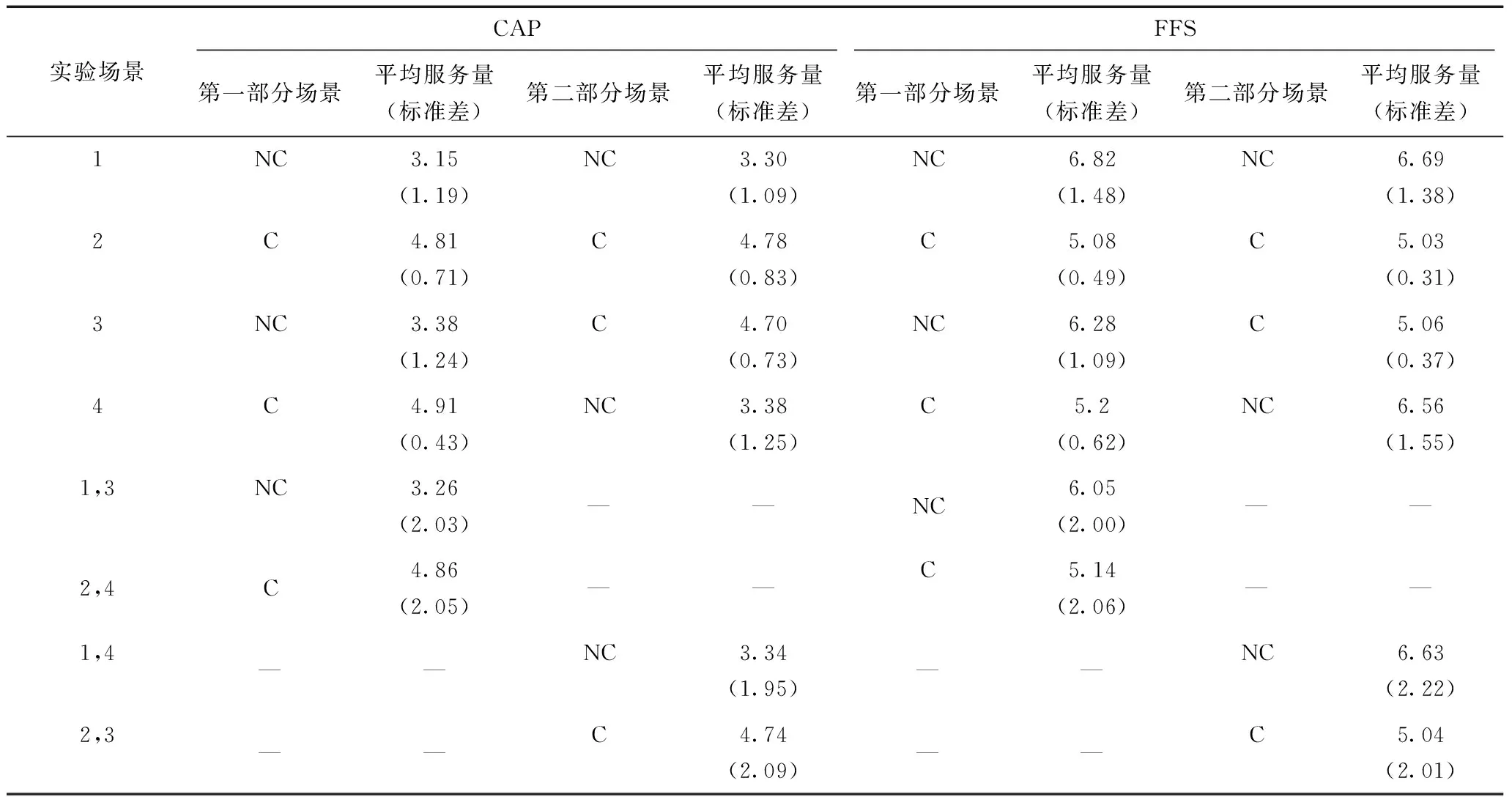
表2 各实验场景平均服务量

利用被试组间与组内比较，发现引入竞争机制纠正不竞争场景下CAP(FFS)服务量供给不足(供给过度)，对医生医疗服务行为带来明显的改变。

3.2 不同疾病种类竞争机制影响

为了比较不同支付方式，不同疾病种类引入竞争机制对医生服务行为带来的改变，以服务量q作为因变量，以竞争场景为自变量(0不竞争，1竞争)，通过随机效应回归模型进行分析。控制变量为教育程度、性别、专业和年龄。通过费舍尔组合检验(Fisher’s Permutation test)获得经验分布，计算经验P值(empirical P-value)，分析各模型间竞争变量系数(竞争机制)之间的差异。

模型1与模型2(模型3与模型4)为轻病(重病)下两种支付方式随机效应回归模型。各模型下竞争变量系数，代表相比于不竞争场景，竞争机制对医疗服务量的影响程度，CAP(FFS)模型1与模型3(模型2与模型4)竞争系数为正(负)，代表相比于不竞争场景，竞争场景医疗服务量增加(减少)，改变不竞争场景下CAP(FFS)供给不足(供给过度)。通过经验P值判断，在轻病下，FFS下竞争变量关联系数1.79个单位大于CAP下1.01个单位(经验P值<0.001，费舍尔组合检验)；在重病下，CAP下竞争变量关联系数1.84个单位大于FFS下0.79个单位(经验P值<0.001，费舍尔组合检验)(表3)。

表3 服务量q不同疾病种类随机效应模型回归

综上，健康状况好的患者FFS下竞争机制影响力度更大，健康状况差的患者CAP下竞争机制对医生行为改变力度更强。

3.3 竞争机制与患者健康效益

研究采用患者健康效益损失比Lj=|B(q*)-B(q)|/B(q)表示相对于患者健康效益最佳医疗服务时患者效益损失(表4)。两种支付方式参数对称式设计下，不竞争场景，相同支付方式和疾病严重程度下患者健康效益平均损失比差异不显著(P>0.393，双侧Mann-Whitney U检验)。

表4 平均患者健康效益损失比

采用患者健康效益损失比为因变量，以竞争场景为自变量(0不竞争，1竞争)，利用面板数据回归进行推断性分析。模型1、3、5为CAP支付方式，模型2、4、6为FFS支付方式，通过费舍尔组合检验分析各模型间竞争机制之间的差异。

模型1-6结果均表明，竞争变量关联系数与患者健康效益损失比呈负相关且具有统计学意义，说明竞争机制引入减少患者健康效益损失。进一步比较CAP轻病与FFS重病(模型3与模型6)，CAP下竞争变量系数略低于FFS下(-0.09vs-0.06,经验P值<0.1，费舍尔组合检验)，提示CAP轻病下竞争机制减少患者健康效益损失程度更大。CAP重病与FFS轻病(模型4与模型5)下竞争系数并未发现统计学差异(经验P值=0.409，费舍尔组合检验)(表5)。相比于FFS，“CAP+竞争机制”减少患者健康效益损失效果更佳，略显制度优势。

表5 患者健康效益损失比随机效应回归模型

3.4 不同场景顺序下医生行为变化趋势

场景3NC-C与场景4C-NC两种支付方式下，两实验场景的竞争场景平均服务量出现差异(P<0.001，双侧Mann-Whitney U检验)，提示不同场景顺序会造成医生行为趋势的改变。

进一步比较各实验局每轮次服务量与最优服务量偏差|q-q*|平均值，在非竞争与竞争场景之间波动情况。CAP下场景1NC-NC与场景2C-C|q-q*|组间变化幅度为1.57,场景3NC-C|q-q*|组内变化幅度为1.36,场景4C-NC|q-q*|组内变化幅度为1.48；FFS下场景1NC-NC与场景2C-C|q-q*|组间变化幅度为1.69,场景3NC-C|q-q*|组内变化幅度为1.21,场景4C-NC|q-q*|组内变化幅度为1.25。

两种支付方式下，各实验场景|q-q*|变化幅度出现统计学差异(P<0.002，双侧Kruskal-Wallis H检验)。相比于场景3NC-C，场景4C-NC不竞争场景与竞争场景服务量偏差变化幅度更大。实验局每轮次|q-q*|折线图可以清楚看出这一趋势(图3)。相比于不竞争转为竞争场景，竞争场景转为不竞争场景医生服务量与最优服务量偏差程度增加，医生医疗服务质量出现降低趋势。

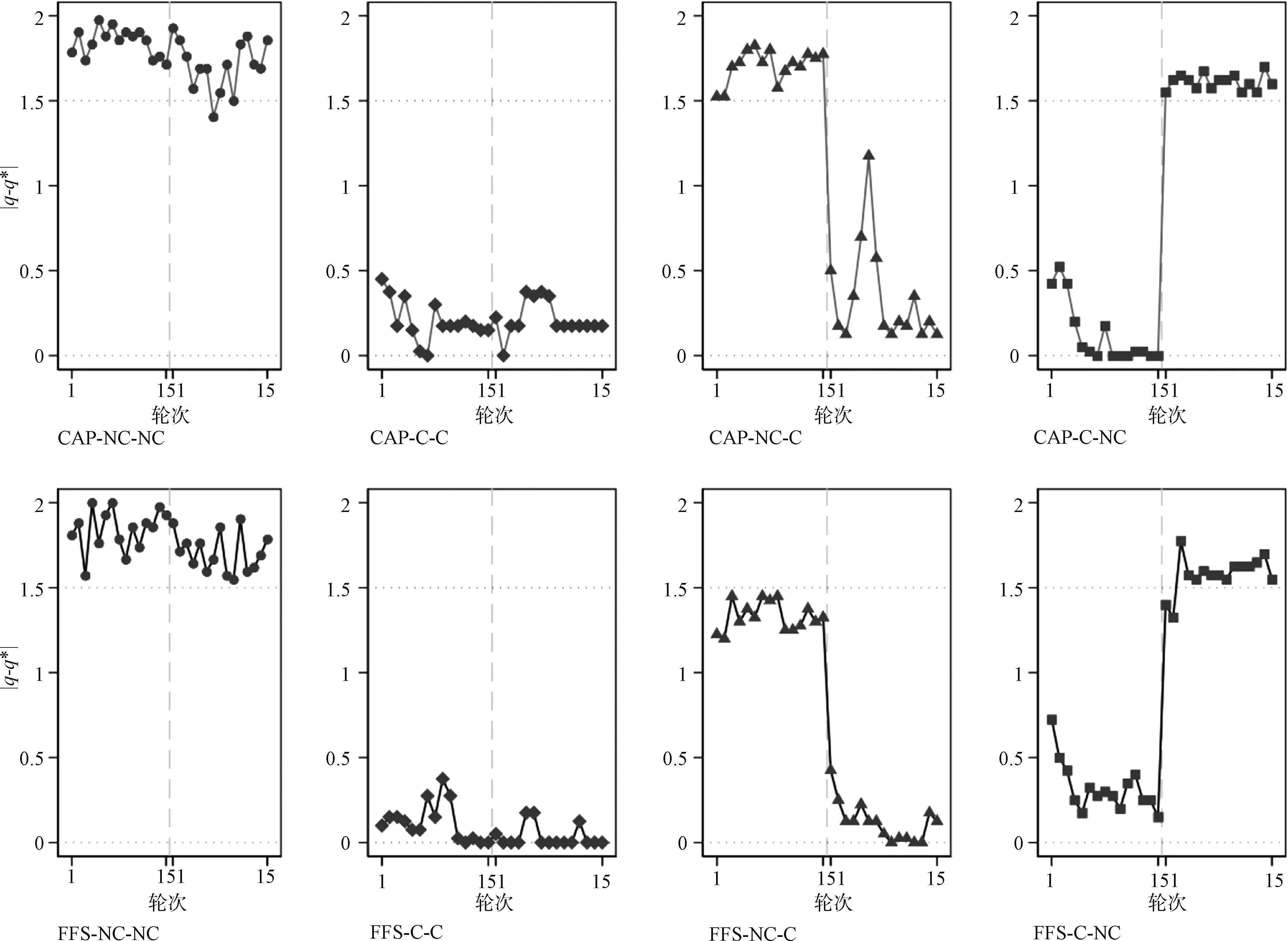
图3 不同实验场景服务量与患者健康效益最优服务量|q-q*|平均偏差折线图

4 讨论

4.1 单一支付方式对家庭医生激励不足，有待探索新机制

家庭医生支付制度方面，国际采取较为通行的CAP支付方式。国内家庭医生签约处于探索阶段，根据目前试点地区与传统模式，在研究设计中将CAP和FFS结合不同场景分别进行探讨。单一支付方式下医生行为研究结果与以往研究保持一致[21-24]，CAP(FFS)不竞争场景下会导致医生服务量的供给不足(供给过度)。因此，目前实验设计可以较好体现不同激励机制下医生行为，在此基础上可以进一步讨论引入竞争机制的影响。

4.2 竞争机制引入家庭医生，提升医疗服务质量

与传统商品市场竞争不同，家庭医生竞争机制多体现于取消患者对家庭医生选择的限制，使得患者拥有更多选择权，形成医患双方相互依赖的组合。2022年《关于推进家庭医生签约服务高质量发展的指导意见》提出优化服务模式允许居民弹性签约，给予患者更多的选择权力。意见明确将服务质量及签约居民满意度等作为评价指标，将考核结果与绩效分配挂钩。推进患者自由选择的竞争机制，促进家庭医生提供有价值的签约服务吸引居民进行签约成为目前的政策方向。

以政策为导向，可以在前期实验研究基础上，模拟患者根据医疗服务质量选择签约的模式，在支付方式基础上探讨竞争机制对医生行为的影响。目前研究结果表明，竞争机制引入会纠正医生行为提高医疗服务质量，与Brosig-Koch等结果一致。[8]

4.3 应注意引入竞争机制配套政策应用情景

区分疾病严重程度，CAP(FFS)竞争机制出现不同效果。非竞争场景下，CAP(FFS)在重(轻)病下较易引起医生提供服务量与患者健康效益最优服务量偏移[23]，引入竞争机制后纠偏效果更佳。两种支付方式结合竞争机制比较中，可以发现“CAP+竞争”机制表现出一定的制度优势。以服务量q作为因变量以及患者健康效益损失比为因变量的分析模型均显示，相比FFS下，“CAP+竞争”制度优势更为显著。另外，不同实验场景顺序对医生行为趋势方面产生一定影响，这也提示在政策制定前，应当衡量政策效果之后决定实施顺序。

4.4 本研究的不足与未来研究方向

考虑到实验研究目的的单一性，本研究以竞争机制引入作为分析重点，选择最常用的两种支付方式进行实验设计，对现实情况进行了适当的简化。现实中家庭医生签约的支付更为复杂，例如家庭医生收入采取事业单位岗位工资与CAP、FFS结合，辅以绩效付费的模式[25]，以及CAP转诊的支付问题在本次设计中尚未涉及。后期研究将逐步纳入这些因素以更加贴合我国家庭医生改革的实际情况。

访谈中发现一些医学生注意到合谋点，但考虑声誉、道德问题的影响，并不会为了追求个人利润而放弃患者效益，体现出医生利他性在医疗决策中的重要意义。应当进一步基于医生效用函数等模型，对医生利他性进行量化分析。