一种简单的精确捕捉接触间断的黎曼求解器
2022-12-19胡立军杜玉龙
胡立军, 杜玉龙
(1.衡阳师范学院 数学与统计学院,衡阳 421002;2.北京航空航天大学 数学科学学院,北京 100191)
1 引 言
基于Godunov型数值格式[1]的有限体积法由于其良好的守恒性和网格适应性,已经成为求解双曲守恒律系统最具代表性的数值方法。通过求解局部黎曼问题来得到网格界面的数值通量是实现有限体积方法的关键步骤。从物理角度来看,采用迭代方法求解黎曼问题的精确解似乎是最合理的,但是由于其效率低且实现难度大,在实际问题的计算中精确黎曼求解器很少使用。因此构造性能良好的近似黎曼求解器一直都是计算流体力学研究的热点问题。
过去几十年,研究人员构造了许多不同性能的近似黎曼求解器。根据捕捉接触间断的能力,可以将其分为两类。非全波求解器,如Rusanov格式[2]、HLLE格式[3]和HLL-CPS格式[4],过高的耗散行为在计算中不能精确分辨接触波或者剪切波;全波求解器,如Roe格式[5]、Osher格式[6]和HLLC格式[7],在计算中能够精确捕捉接触间断和剪切波。但是,在计算强激波问题时,这些低耗散的求解器会遭遇严重的不稳定现象,这大大限制了它们在高超声速流动问题中的应用。
研究人员尝试在保留全波求解器精确分辨接触间断优点的同时来消除它们的激波不稳定性,其中最流行的方法是根据当地流场在耗散格式和低耗散格式之间进行切换的混合方法[8-12]。尽管混合格式可以成功地抑制激波失稳现象,但是对于复杂的流动问题,不恰当的开关函数可能会影响接触间断的分辨率,并且两种格式间的突然切换也可能会影响到格式的收敛速度[13]。此外,增加多维耗散也是抑制全波黎曼求解器激波失稳现象的一种常用方法,主要通过增加格式的剪切粘性[14,15]、构造旋转黎曼求解器[16,17]或者法向速度重建技术[18]来实现。旋转格式在每个网格界面处需要计算两次数值通量,因此计算效率低。而单纯地增加剪切粘性在某些情形下并不能完全消除激波异常现象[19]。最近,Chen等[20]通过在动量通量中引入剪切粘性构造了一种具有良好激波稳定性的HLLC+格式。
此外提高非全波黎曼求解器的接触捕捉精度也是构造性能良好的数值格式的一种策略。本文利用双曲正切函数[21]来重构界面两侧的密度值,并且结合边界变差递减算法[22]来减小单波Rusanov格式耗散项中的密度差,从而提高格式分辨接触间断的能力。数值结果表明,本文构造的黎曼求解器比全波的HLLC格式具有更高的接触分辨率和更好的激波稳定性。
2 背景知识
守恒形式的二维欧拉方程组为
(1)
式中
(2)

(3)
本文的比热比γ取1.4。
采用有限体积法对式(1)进行空间离散,可以得到半离散方程为
(4)
式中Ui,j为守恒向量U的单元平均值,Fi +1/2,j和Gi,j +1/2为数值通量。式(4)可以改写成ODE系统为
dU/dt=L(U)
(5)
2.1 时间离散
采用优化的三阶TVD龙格-库塔格式[23]来进行时间离散,
U(1)=Un+ΔtL(Un)
(6)
式中Δt为时间步长。
2.2 五阶WENO格式
采用五阶WENO格式[24]重构得到界面左右两侧的状态值为
(7)
(8)
非线性权重系数定义为
(9)

(10)
式(7)的线性加权系数为
(11)
而式(8)的线性加权系数为
(12)
为防止分母为0,取ε=10-6。
利用WENO重构得到界面左右两侧的状态值,然后利用近似黎曼求解器求解局部黎曼问题,从而得到每个网格界面处的数值通量。
2.3 Rusanov求解器
最简单的单波Rusanov黎曼求解器[2]的数值通量函数为
(13)
波速S定义为
S=max(|uL-aL|,|uR-aR|,|uL+aL|,|uR+aR|)
(14)
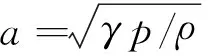
2.4 HLLC求解器
全波的HLLC黎曼求解器的数值通量函数为
(15)
式中
(16)
波速估计为
(17)

3 一种精确分辨接触间断的Rusanov黎曼求解器
Rusanov格式的通量函数式(13)可以改写为
(18)
式中右端第一项为中心差分项,D1/2为耗散项,其表达式为
(19)
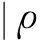
(20)
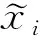
(21)
为了计算方便,本文直接给出网格界面左右两侧密度重构值的计算公式为
(22)
式中


(23)
式中β为控制密度跳跃大小的参数,本文取β=1.6。
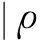
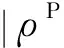
(24)
将由式(24)确定的界面两侧的密度值代入式(19)计算耗散项D1/2,从而得到一种低耗散的Rusanov格式(命名为LD -Rusanov,Low Diffusion Rusanov)。此外,本文为了提高非线性波的分辨率,采用Roe平均值来计算波速,

(25)
在计算多维问题时,采用算子分裂方法来逐维计算数值通量。因此本文所述的一维算法可以直接应用于每个坐标方向。双曲正切重构作为一种代数方法,在进行多维计算时不会涉及到任何的几何重构,因此实施起来比较简单。此外,与HLLC格式通过修改HLL格式的波系结构来提高接触波的分辨率不同的是,LD-Rusanov格式采用代数方法而不是修改原Rusanov格式的波系结构来提高接触间断的捕捉能力,因此其很好地保留了原Rusanov格式的激波稳定性。接下来,通过一系列的数值实验来证明LD-Rusanov格式的高分辨率和强鲁棒性。
4 数值结果
通过一些典型的数值算例来验证LD -Rusanov格式的表现。
4.1 孤立的接触间断
首先考虑一个孤立的慢行接触波,计算区域为[0,1],其初始条件为
(26)
计算中使用网格数为100的均匀网格。从 图1 可以看出,本文构造的LD -Rusanov格式不仅可以更加精确地捕捉该接触间断,而且还消除了原Rusanov格式在间断附近出现的过冲。图2展示了取不同β值的LD -Rusanov格式计算该算例时的计算结果。可以看出,β=1.3,1.6和1,9都可以得到精确的结果。为了定量分析不同β值对于结果的影响,采用式(27)来计算间断的厚度,
(27)


图1 孤立的接触间断在t =3时的密度分布
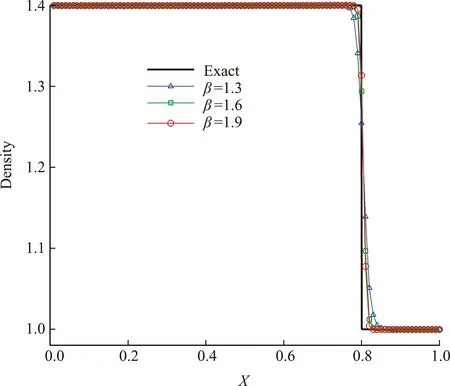
图2 取不同β值的LD -Rusanov格式的密度分布
由表1可知,β值越大,间断的厚度越小,其分辨率也会越高,但是过大的β会卷起平行于速度方向的界面[21]。本文发现1.2~2.0的β值可以得到令人满意的结果。
4.2 一维爆轰波问题
计算区域为[0,1],初始条件为
(28)
计算中使用网格数为200的均匀网格。该算例的解由两个相互作用的爆轰波形成的复杂间断结构构成。从图3可以看出,相比原始的Rusanov格式和全波的HLLC格式,本文构造的LD -Rusanov格式能够更加精确地捕捉各个波系。
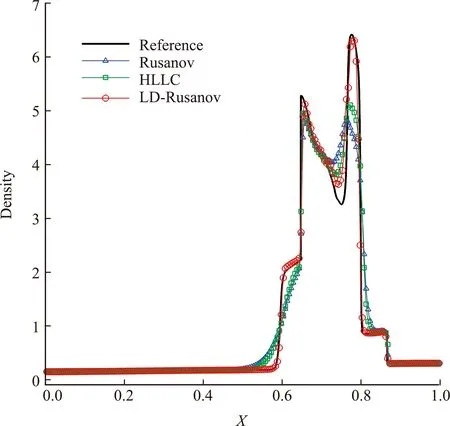
图3 一维爆轰波问题在t =0.038时的密度分布
4.3 Titarev-Toro问题
考虑Titarev等[24]提出的激波-熵波相互作用问题。计算区域[-5,5]均匀划分成500个网格,初始条件为

(29)
该算例涉及到高频振荡的正弦波和激波的相互作用。从图4可以看出,Rusanov格式的计算结果具有较大的数值耗散,而本文构造的LD -Rusanov格式得到了更加精确的解,在捕捉高频波时比全波的HLLC格式具有更高的分辨率。

图4 Titarev-Toro问题在t =5时的密度分布
4.4 二维爆炸问题
二维爆炸问题是一维Sod问题的推广,计算该算例来检验格式捕捉不同波系的能力。计算区域[-1,1]×[-1,1]均匀划分成101×101的正方形网格,初始条件为

(30)
计算时间为t=0.25。此时,该算例的解由一个向外运动的圆形激波和接触面以及向中心运动的稀疏波构成。图5展示了时间t=0.25时沿径向y=0的密度分布。可以看出,本文构造的 LD -Rusanov 格式能够精确地捕捉各个波系,特别是对接触间断的分辨率明显优于原始的Rusanov格式和HLLC格式。

图5 二维爆炸问题在t =0.25时的密度分布
4.5 移动的圆形接触面问题
计算区域[0,1]×[0,1]划分成100×100的均匀网格,其初始分布为

(31)
该算例的解由一个以匀速(u,v)=(1,1)运动的圆形接触面构成。在t=0.3时刻该问题的精确解为

(32)
从图6可以看出,相比于原始的Rusanov格式和全波的HLLC格式,本文构造的LD -Rusanov格式对于该圆形接触面具有更高的分辨率。

图6 移动的圆形接触面问题的计算结果
4.6 奇偶失联问题
本文数值实验表明,在捕捉接触间断时LD -Rusanov格式比HLLC格式具有更高的分辨率。文献[8-20]曾报道精确分辨接触间断的数值格式(如HLLC格式)在计算多维强激波问题时会出现严重的不稳定现象。接下来,计算几个典型的强激波问题来检验LD -Rusanov格式的鲁棒性。
首先,计算Quirk[8]提出的奇偶失联算例来评估格式的激波稳定性。马赫数为20的平面运动激波从左向右传播,其初始位置为x=5。右侧的波前状态为(ρ,u,v,p)R=(1.4,0,0,1),左侧的波后状态由Rankine-Hugoniot关系式计算得到。计算区域[0,600]×[0,20]分割成600×20的矩形网格,且y-方向的网格中心线上存在±10-3的奇偶小扰动。图7展示了t=20时的密度等值图,为了全面比较格式的激波稳定性,本文还展示了两种稳定版本的HLLC格式(HLLCM[13]和HLLC+[20])的计算结果。可以看出,HLLC格式表现出了明显的激波失稳现象,而LD -Rusanov格式和另外两种稳定版本的HLLC格式均得到了稳定的激波面。

图7 奇偶失联问题的密度等值图
4.7 稳态斜激波问题
接下来考虑稳态斜激波问题[26]。计算区域[0,50]×[0,30]划分成50×30的正方形网格,沿着直线y=2(x-12)有一个稳态激波,其波前状态为(ρ,u,v,p)L=(1,447.26,-223.5,3644.31),波后状态(ρ,u,v,p)R=(5.444,82.15,-41.05,207725.94)。图8展示了时间迭代1000步的计算结果。可以看出,全波的HLLC格式出现了明显的激波不稳定现象,而LD-Rusanov格式保留了原始Rusanov格式的稳定性,得到了清晰的激波面。
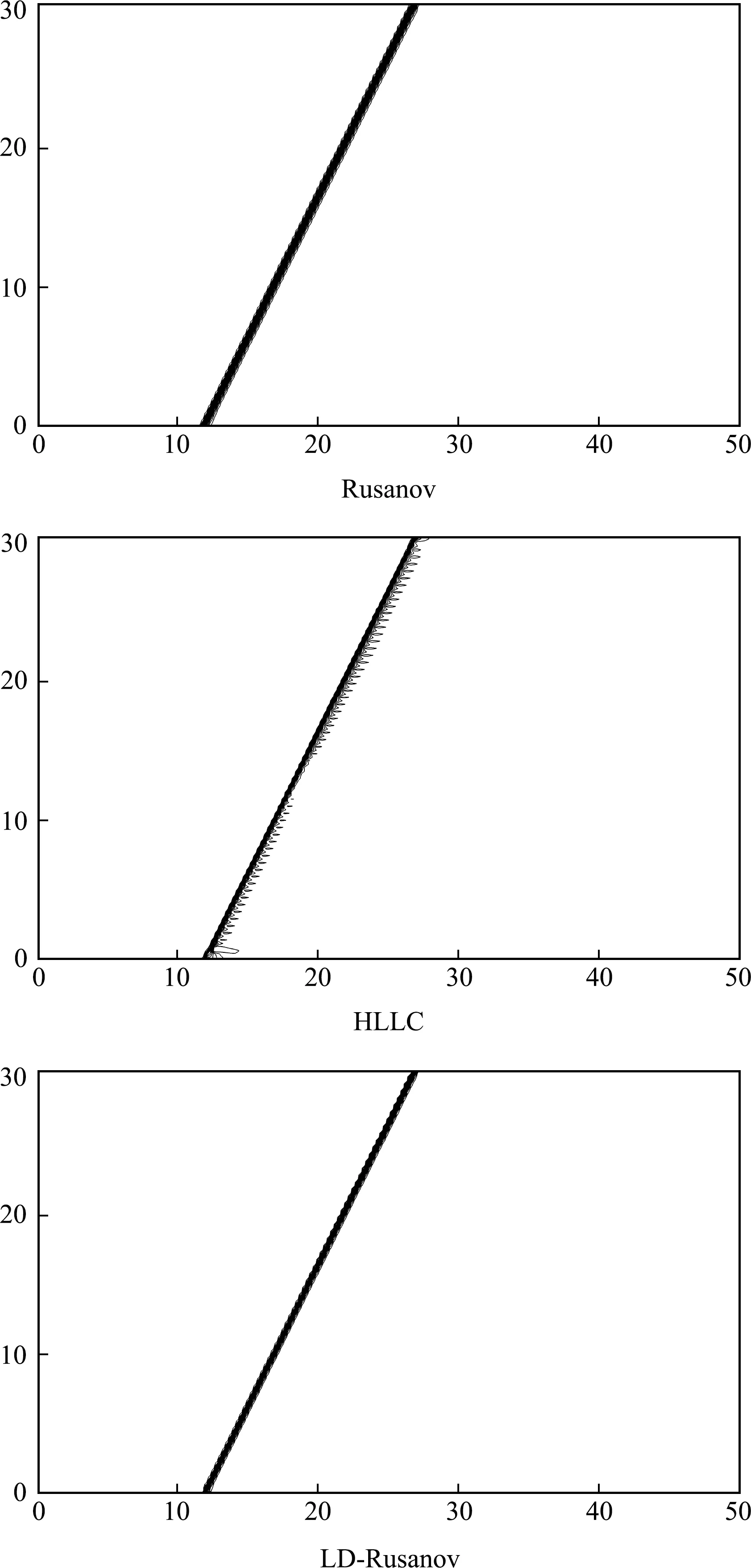
图8 稳态斜激波问题的密度等值线
4.8 圆柱绕流问题
计算马赫数为20的无粘圆柱绕流问题来评估不同数值格式在高超声速流动问题中的激波稳定性。该算例具体的计算区域和初边值条件的描述参考文献[12]。本文采用40×80的非规则结构四边形网格来划分计算区域。图9展示了t=4时的密度等值图。可以看出,HLLC格式表现出明显的激波失稳现象,出现了严重的红玉现象,而LD -Rusanov格式和另外两种稳定版本的HLLC格式均得到了稳定的数值解。
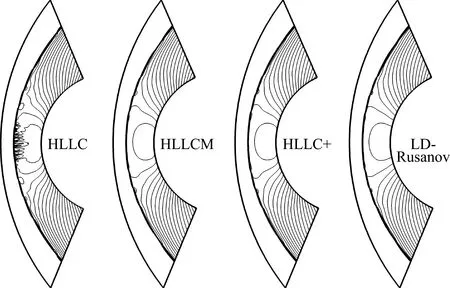
图9 无粘圆柱绕流问题的密度等值图
4.9 正激波绕射问题
计算马赫数为5.09的正激波绕射问题来验证格式的鲁棒性。采用200×200的均匀网格来划分计算区域[0,1]×[0,1],其中角点位于(x,y)=(0.05,0.6)处。初始时正激波右侧静止流体的密度为1.4,压力为1。角点上方左侧的入口边界条件可以由Rankine -Hugoniot关系式计算得到,区域底部和角点下方左侧设置为反射边界条件,在右边界所有变量的梯度设置为零,区域顶部的边界条件会随着激波的运动而调整。图10展示了t=0.15 时的密度等值图。可以看出,HLLC格式在正激波的上方出现了明显的激波失稳现象,而LD -Rusanov格式和另外两种稳定版本的HLLC格式均得到了稳定的正激波。值得注意的是,在该算例中本文构造的LD -Rusanov格式表现出了最好的稳定性。

图10 正激波绕射问题的密度等值图
5 结 论
基于单波的Rusanov求解器构造了一种低耗散的LD -Rusanov黎曼求解器。使用双曲正切函数和五阶WENO格式来重构界面两侧的密度值。利用边界变差下降算法从密度重构值的不同组合中挑选出使界面两侧密度差最小的密度值,从而最大限度地减小Rusanov求解器耗散项中的密度差,进而提高格式对于接触间断的分辨率。全波的HLLC格式通过修改HLL格式的波系结构来提高接触间断的分辨率,因此无法保留HLL格式的激波稳定性。本文构造的LD -Rusanov格式使用一种代数方法来提高接触间断的捕捉能力,并没有修改原Rusanov求解器的波系结构,因此很好地保留了Rusanov的激波稳定性。一系列数值实验表明LD -Rusanov格式比全波的HLLC格式具有更好的接触间断捕捉能力和鲁棒性。本文构造的低耗散数值格式展现出了良好的应用前景,因此将其应用于复杂流动问题(如可压缩湍流和化学反应流)的数值模拟值得未来进一步的研究。
