圆锥曲线中最值问题的破解策略

许发君

(广西柳州市第一中学)

圆锥曲线中的最值问题一直是历年高考中命题的热点之一,是解析几何中的综合问题,各种题型都有,命题角度很广,备受命题者青睐.破解圆锥曲线中的最值问题总体概括起来有两大策略:一是利用几何方法,通过利用圆锥曲线的定义、几何性质以及平面几何中的定理、性质等合理转化,再根据数形结合思想方式巧妙求解;二是利用代数法,通过把要求最值的几何量或代数表达式表示为某个(些)参数的函数(解析式),然后利用函数以及不等式等方法分析与求解.本文结合历年高考中最常见的圆锥曲线最值问题,从几何法或代数法的角度分析与处理问题,总结规律,归纳技巧方法与策略,以期引领并指导备考.

1 几何法——利用定义性质转化法求最值

定义性质转化法是指利用圆锥曲线的定义和性质求最值,常用它解与圆锥曲线上的点到焦点的距离(抛物线还涉及曲线上的点到准线的距离)有关的问题.

利用几何法破解此类求最值问题的关键需过好四关:一是方程(组)关,即会利用方程(组)求出参数的值;二是公式关,即会利用过两点的直线的斜率公式,求出直线的斜率;三是转化关,如本题,把证明三点共线转化为证明任意两点的连线所在直线的斜率相等,当然也可以转化为向量共线;四是最值关,会利用基本不等式等方法求最值.

2 代数法——利用目标函数法求最值

目标函数法就是通过设参及坐标运算建立关于所求问题的函数解析式,进而根据已知条件求出变量的取值范围.破解此类题的关键点如下.

1)定变量,即根据题意确定变量及其取值范围(目标函数的定义域).

2)建立目标函数,即利用定义或公式(点到直线的距离公式、两点间的距离公式、斜率公式等),通过坐标运算,建立目标函数.

3)定最值或定范围,即根据目标函数解析式的结构特征,采用配方法、基本不等式法、函数的有界性及单调性(可以利用导数研究)等确定最值或取值范围.

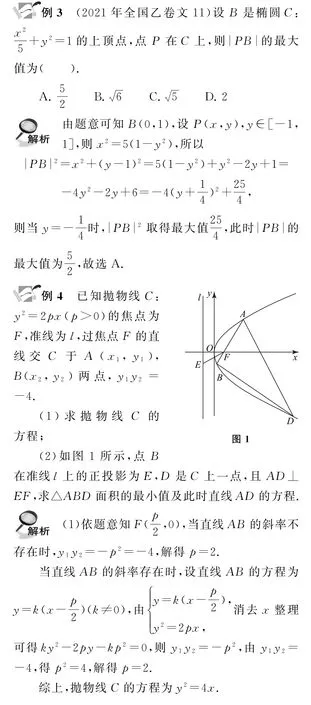
利用代数法解决圆锥曲线中的最值问题,要注意联系圆锥曲线的定义和性质,结合换元思想或引入参数,将问题转化为一定的函数关系或不等式问题进行讨论.

圆锥曲线中的最值问题题型新颖,类型众多,形式各样,解法灵活多变,要求具有较强的综合应用能力.破解此类问题,有章可循,有法可依,若题目的条件和结论能明显体现几何特征及意义,可以考虑从几何视角切入,数形结合,直观处理;若题目的条件和结论能体现一种明确的函数关系,可以考虑从代数视角切入,构建函数求解.