一道课本例题到一道高考试题的衍变之路

高 磊

(山东省青岛第二中学)

每一道高考试题追根溯源都是一道课本题目的延伸和衍变,因此课堂教学要紧扣教材,对例题开展深度研究.本文阐述一道例题逐步衍变成一道道高考试题的过程,通过对圆锥曲线性质进行逐层剖析,探寻课本例题与高考试题之间的联系,为高三复习提供新视角.

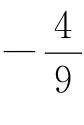
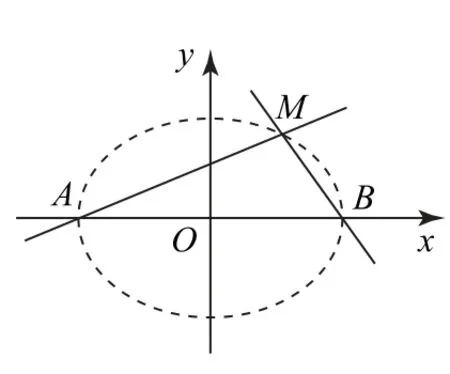
图1

1 衍变第一步:调换例题的已知和结论

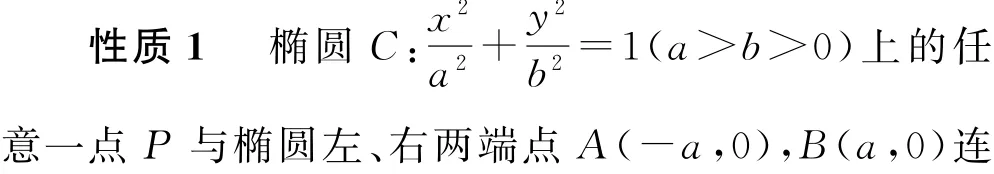
2 衍变第二步:将定弦AB 改为过原点的动弦AB

3 衍变第三步:过原点的动弦AB 改为过定点T(t,0)的动弦

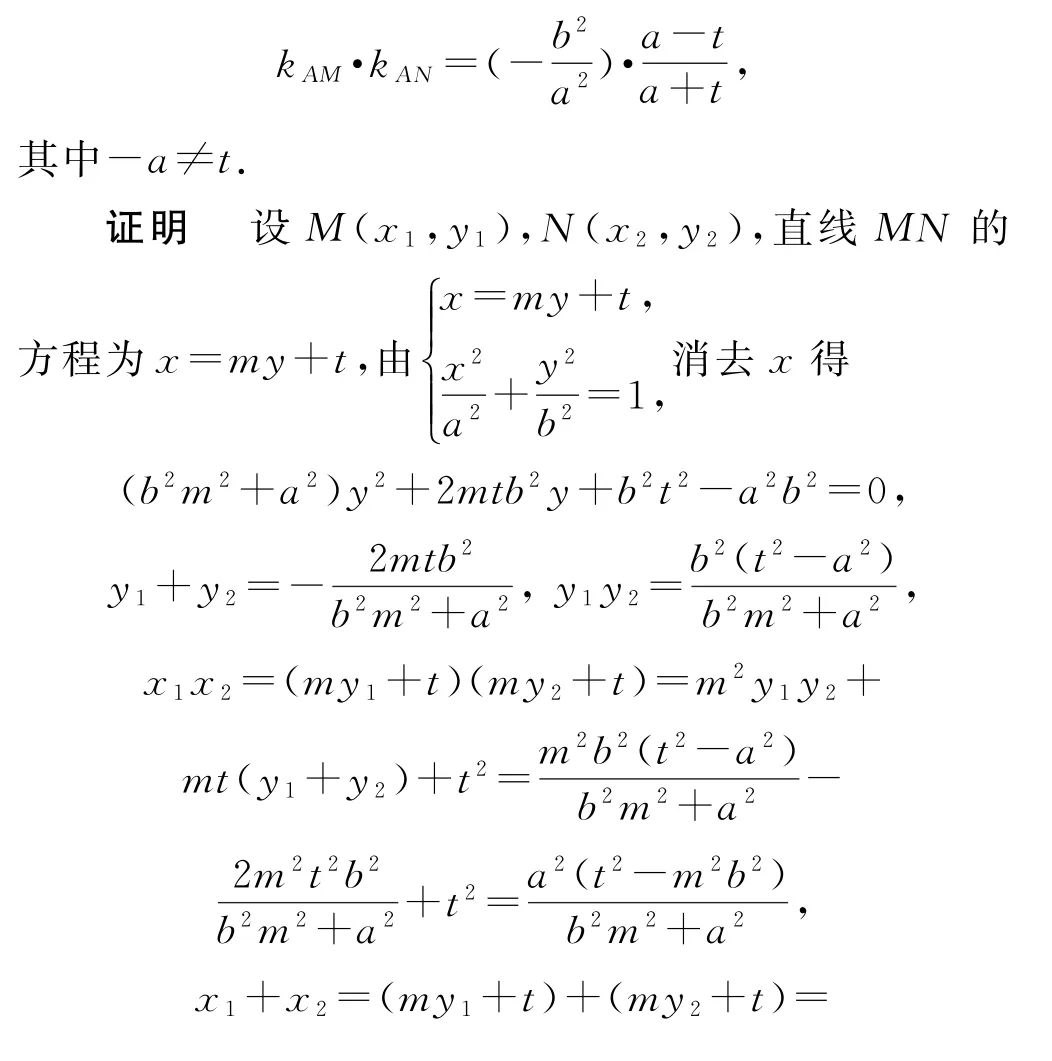
图2

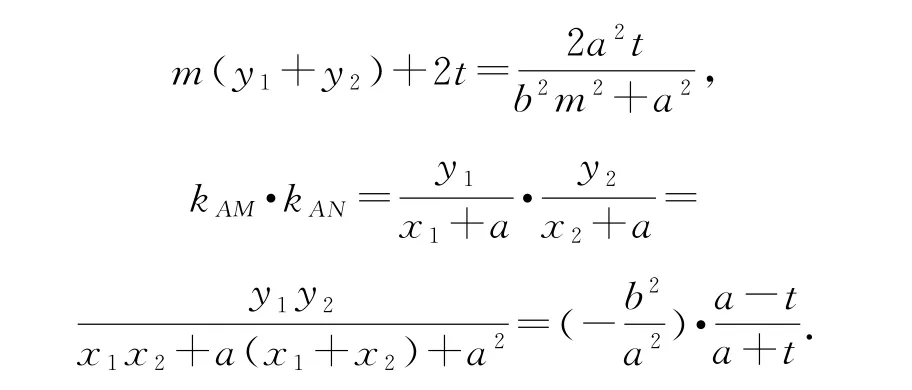
4 衍变第四步:过定点T(t,0)的动弦端点与长轴两端点连接形成蝴蝶三角形

图3

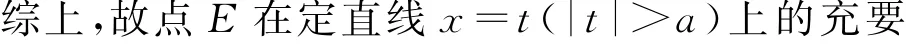
5 衍变第五步:蝴蝶定理与圆锥曲线相结合

蝴蝶定理(ButterflyTheorem):设P为圆内弦AB的中点,过P作弦EF和CD,设CF和DE与AB分别相交于点M和N(如图4),则P是MN的中点.

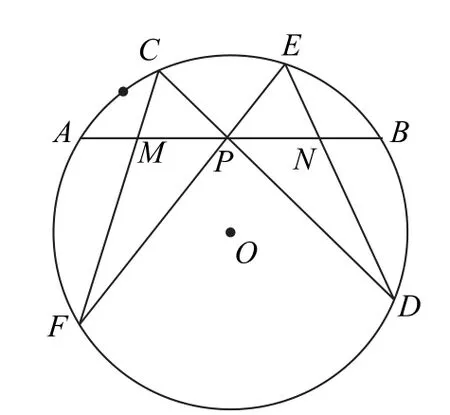
图4

此定理还可以推广到椭圆、双曲线和抛物线中,下述只证明在椭圆中的情形.

证明 设P(m,n),A(x1,y1),B(x2,y2).

6 衍变第六步:将性质3的条件和结论对调

一道试题通常包括显性要素和隐性内涵,显性要素就是能看到的情境与设问形式,而教学中要引导学生对其隐性内涵做进一步探讨、迁移,引导学生更好地把握数学问题的本质,提升学生的数学素养.

7 衍变第七步:试题迁移与拓展

7.1 试题迁移

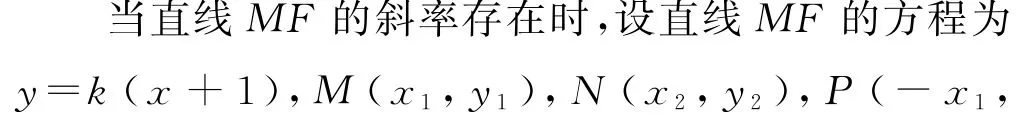
圆锥曲线中的定点与定值问题一直是高考的热点,解决此类问题常见的方法有两种:

一是从特殊入手,求出定点、定值,再证明这个定点、定值与变量无关;

二是通过引入参数,并在计算推理过程中消去参数,从而得到定点、定值.

7.2 试题拓展

对例5的第(2)问进行如下变式.

变式1 设点F(－1,0),直线MF与曲线C相交于点N,证明:kAM·kAN为定值.

变式3 设直线l与曲线C相交于两点M,N,若直线MB与直线AN的斜率存在,且kAN＝3kBM,证明:直线MN过定点.

分析 由性质6可知直线MN过定点(－1,0).

变式4 设点F(－1,0),直线MF与曲线C相交于点N,设直线MB与直线AN相交于点E,证明:点E在定直线上.

分析 由性质4可知点E在定直线x＝－4上.

高考真题是复习备考的重要素材,每一道高考题都含有丰富的数学内涵,也体现了很多命题专家的心血和智慧.教师应探本求源,建立高考试题与教材的对接点,并以高考为导向挖掘其隐含的复习资源,立足教材,引导学生把握通性通法,引导学生在数学学习中注重对基础知识进行梳理归纳,形成知识网络;明确典型例题的解题思路,总结解题方法,触类旁通,探究解题规律.只有夯实双基、突出重点,才能以不变应万变.