换元法在解题中的应用

⦿哈尔滨师范大学教师教育学院 邹佳珊

换元法又称辅助元素法、变量代换法，是在解题的过程中引进新的变量，把分散的条件联系起来，隐含的条件显露出来，或者把条件与结论联系起来，变为熟悉的形式，把复杂的计算和推理论证过程简化.换元法是高中数学解题中的一类重要而巧妙的解题方法.在数学中，“元”是未知数的意思，我们在解题中经常遇到含有未知数的情形，例如方程、不等式、函数等.利用换元法来解决这类问题，不仅有利于快速找到解题思路，而且解题过程方便灵活，掌握换元法的基本思想及方法对提升数学解题能力大有益处[1].

常见的换元方法有整体换元、三角换元等，下面以具体的习题为例，探究何时可以利用换元法解题.

1 整体换元法的应用

当某个代数式作为“整体”反复多次出现，为了简化计算，可以将重复出现的部分进行“换元”处理.

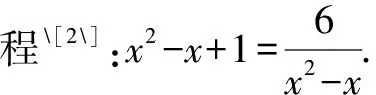
为何“换元”：此题如果直接去分母进行求解，会得到一个四次方程.通过观察可以发现x2-x既在等式左边出现，又是等式右边的分母，把这一部分替换成另一个未知数，可以达到降幂的效果，将难解的高阶方程化为熟悉的一元二次方程.

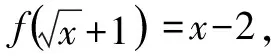
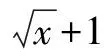
把x=(t-1)2代入原解析式中，则f(t)=t2-2t+3(t≥1).

我们知道，对应关系与自变量取哪个字母无关，故f(x)=x2-2x+3(x≥1).

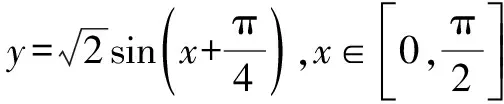
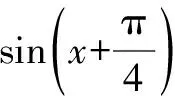
理解换元法的本质进而用换元法来求函数的值域是高中数学的重要知识点.本题比较简单，虽然也可以利用其他方法来求解，但是对学生理解换元法的内涵有启发作用[3].

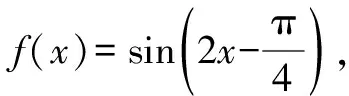
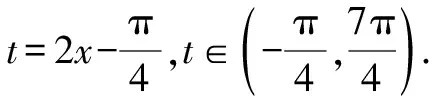
图1

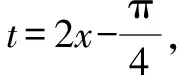
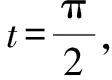
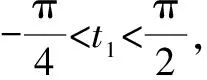
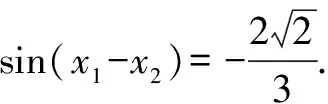
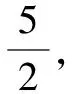
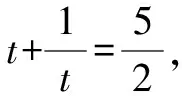
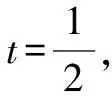
2 三角换元法的应用

三角换元常用于去根号，或者将代数式变换为三角形式更易求解.主要利用已知代数式与三角知识的某种联系进行换元.

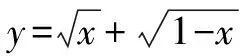
为何“换元”：不难发现x的取值范围是{x|0≤x≤1}，恰好是正弦函数y=sinx值域的子集，我们又有去根号的需要，希望可以通过换元将被开方数的次数变为2.

如变量x，y适合条件x2+y2=r2时，也可以作三角代换：x=rcosθ，y=rsinθ.

例7(2020年清华大学强基计划)若x2+y2≤1，则x2+xy-y2的取值范围是.

为何“换元”：前面已经提到了x2+y2=r2的换元方法，此题不过是对r的取值范围做了限制.

如何“换元”：，若设x=rcosθ，y=rsinθ，θ∈[0,2π)根据题意可知r≤1，则

x2+xy-y2

=r2cos2θ+r2cosθsinθ-r2sin2θ

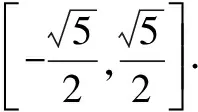
例8(2020年复旦大学强基计划)已知实数x,y满足x2+2xy=1，求x2+y2的最小值.

为何“换元”：看到x2+y2=r2， 依然是三角换元法的常见形式，可以先换元，再检验是否可行.

如何“换元”：设x=rcosθ,y=rsinθ,θ∈[0,2π)，代入x2+2xy=1中，可以得到r2cos2θ+2r2sinθcosθ=1.由于我们要求的是r2，因此整理得

根据辅助角公式,可得

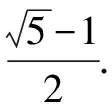
本题启发我们，x2+y2=r2无论是在题干中出现，还是求它的取值范围，都可以考虑利用三角换元法来求解.

孔子曰：“举一隅不以三隅反，则不复也.”经过以上几道例题的分析，可以总结得出何时应用换元法解题：若题目中有重复出现的部分，则常常可以对重复出现的部分进行换元，利用整体换元法求解；而三角换元法则往往是被换元部分的取值范围与三角函数值的范围[-1,1]或(0,1)等相关，或有“去根号”的需要，合理利用同角三角函数的基本关系式、三角恒等变换、辅助角公式等进一步化简求值.