基于最小关键支配结构的电力光缆网骨干网络挖掘算法

姜万昌，刘艳辉，郭 健，王圣达，刘丹妮

基于最小关键支配结构的电力光缆网骨干网络挖掘算法

姜万昌1,2，刘艳辉1,2，郭 健3，王圣达4，刘丹妮4

(1.东北电力大学计算机学院，吉林 吉林 132012；2.东北电力大学吉林省智能电网信息技术工程实验室，吉林 吉林 132012；3.吉电集团有限公司丰满配电施工处，吉林 吉林 132000；4.国家电网吉林省电力有限公司信息通信公司，吉林 长春 130021)

电力光缆网骨干网络为包含重要通信站点、枢纽站点、桥接链路等关键实体，且满足连通约束的最小规模电力光缆网主干网架。为挖掘电力光缆网骨干网络，设计基于最小关键支配结构的骨干网络挖掘算法。首先，根据省级电力光缆网物理拓扑结构，构建电力光缆网表示模型。其次，提出基于最小关键支配结构的关键边度量方法，识别电力光缆网关键边。最后，设计基于最小关键支配结构的电力光缆网骨干网络挖掘算法，实现对电力光缆网骨干网络的挖掘。使用吉林省省级和南部电力光缆网设计两组实验，运用所提算法和两种经典方法挖掘骨干网络，据此对电力光缆网模拟蓄意攻击，对比分析网络连通性的变化趋势，以验证所提算法的有效性。

最小关键支配结构；复杂网络；电力光缆网；骨干网络

0 引言

电力光缆网是保证电力系统安全稳定运行的专用通信网络[1-2]，由通信站点内的设备以及连接这些设备的电力光缆构成[3]。随着电力光缆网络复杂性日益增加，通信站点、枢纽站点、桥接光缆链路等关键实体发生故障的频率也在逐渐上升[4-5]。自然灾害、中断故障、外力破坏等意外事故都可能造成电力光缆网关键实体的故障甚至退运。不仅如此，早期建立的光缆链路由于线路老化或遭受电腐蚀等，故障次数也在逐年增加[6-7]。电力光缆网中重要通信站点、关键链路等一旦发生故障，会对电力光缆网络造成网络拥塞、传输性能下降[8-9]、网络不连通等问题[10-11]。若能事先挖掘出包含重要通信站点、枢纽站点、桥接链路等关键实体，且满足连通约束的电力光缆网最小规模主干网架，那么在灾害时期，只须保障最小规模电力光缆网安全就可维持电力光缆网的基本通信，对保证电力光缆网通信的可靠性具有重大意义。

目前，有多位学者在复杂网络及电网、生态网络等领域对骨干网络关键实体挖掘进行了初步研究。文献[12]提出了基于需求差异化的骨干网架构建方法用于挖掘负荷、电源和网架需求的主干网架。文献[13-14]运用基于最小连通支配集的关键节点与连边挖掘方法挖掘网络的主干网架。文献[15]利用边介数和最小生成树的概念，识别生态网络中的主干通道，但该方法时间复杂度较大。文献[16]将图的最小骨架定义为由最小连通支配集内的节点所主导的子图，由此形成的骨干网络边数目和节点数目过多，不符合经济合理性原则。

现有的电力光缆网关键实体挖掘方法仅挖掘关键节点或关键链路个体。文献[17]从拓扑结构上提出链路重要度，进行光通信网挖掘。文献[18]考虑节点承担的通信业务及节点在电网中的位置及影响，构建多指标评价体系辨识电力通信网中的关键节点。文献[19]提出一种基于多属性决策的电力通信网节点重要性计算方法。现有研究未从骨干网络整体层次进行考虑，并且度量因素指标较为单一，无法有效挖掘包含重要通信站点、枢纽站点、桥接链路等关键实体的网络结构。

本文设计基于最小关键支配结构的电力光缆网骨干网络挖掘算法，使用吉林省省级和南部电力光缆网的物理拓扑结构，构建电力光缆网表示模型，运用本文提出的骨干网络挖掘算法与最小连通支配集和边介数最小生成树挖掘算法挖掘骨干网络，据此模拟蓄意攻击电力光缆网表示模型，对比分析骨干网络对网络连通性造成的影响，验证了所提方法的有效性。

1 电力光缆网表示模型

本节通过电力光缆网物理拓扑结构建立电力光缆网与网络模型之间的映射关系，构建描述省级电力光缆网物理网络的电力光缆网表示模型，具体规则如下：

1) 将省级电力光缆网中省调、备调、地调、500 kV变电站、220 kV变电站、66 kV变电站、用户变电站、电厂中的通信站点均抽象为无差别的节点；

2) 电力光缆网中的调度、发电厂和变电站之间采用光缆链路进行通信连接。将各通信站点之间的光缆链路抽象为边，忽略各光缆链路的长度、芯数和电压等级，将电力光缆网链路等效为无权边；

3) 由于电力光缆网中信号的传输是双向的，故将电力光缆网链路等效为无向边；

4) 合并两个通信站之间两条光缆链路，将光缆网拓扑结构中的双重链路视为单边。

为确保电力光缆网安全稳定运行，以及有效主动防御事故造成的冲击[20-21]，应准确高效地挖掘出电力光缆网中的骨干网络。骨干网络是以电力光缆网遇到破坏时依旧保持电力光缆网主干网架的稳定通信为目的，是包含重要通信站点、枢纽站点、桥接链路等网络关键实体，满足连通约束的最小规模电力光缆网主干网架，须要满足以下条件：

1) 骨干网络中必须留存重要通信站点、枢纽站点、桥接链路等关键实体；

2) 骨干网络必须满足连通性约束，以保证电力光缆网稳定的信息通信；

3) 骨干网络中保证拓扑连通性的链路及站点数目应尽可能少；

4) 未在骨干网络上的站点保证在一跳的距离到达骨干网络，确保电力光缆网高效通信。

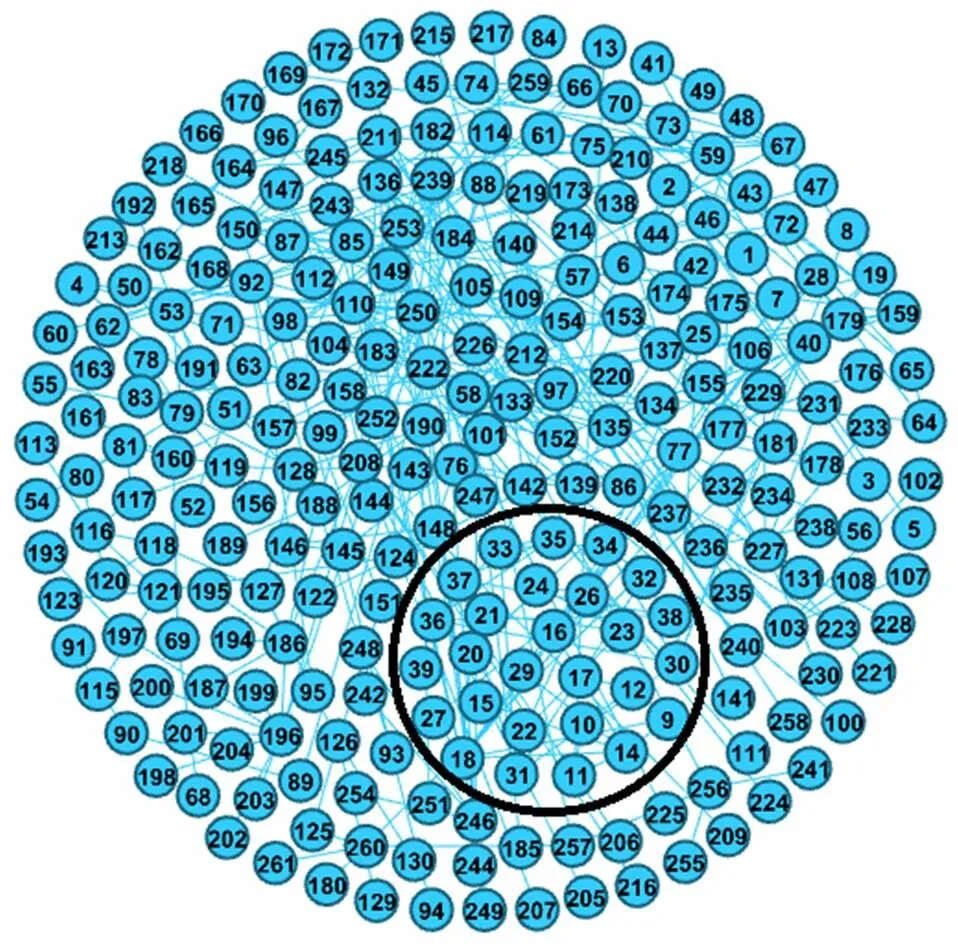
图1 省级电力光缆网表示模型

图2 局部省级电力光缆网表示模型

2 基于最小关键支配结构的关键边度量

2.1 骨干边集

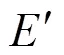
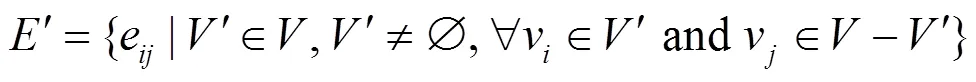
2.2 关键支配结构

考虑到骨干网络中应包含重要通信站点、枢纽站点、桥接边以及两端的节点，为挖掘电力光缆网表示模型中重要通信站点、枢纽节点、桥接边以及两端的节点，运用所提出的电力光缆网桥接边挖掘算法[22]，在此基础上挖掘桥接边，将电力光缆网中节点和边的特征信息与拓扑势融合，设计关键支配结构，用于初步选择构成骨干边集的关键边及两端端点。其计算过程如式(3)所示。

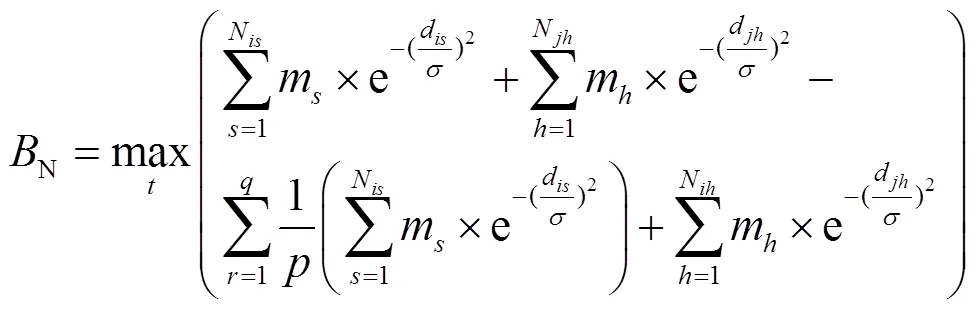
2.3 最小关键支配结构

关键支配结构能够度量出关键边集及关键边的两端节点集，但这些边集和节点集构成的网络结构并不满足连通约束。因此为保证关键支配结构是满足连通约束的最小规模电力光缆网主干网架，且关键支配结构中保证拓扑连通性的链路及节点尽可能重要，设计基于最小关键支配结构的关键边度量方法，用于补充并选择最终构成骨干网络的骨干边集及节点集，计算过程如式(4)所示。

使用上述公式可获得电力光缆网表示模型中边的基于最小关键支配结构的关键边度量值，当边的度量值越大时，则这条边及两端边端点构成电力光缆网骨干网络的可能性越大。

3 电力光缆网骨干网络挖掘算法

为挖掘电力光缆网骨干网络，设计基于最小关键支配结构的电力光缆网骨干网络挖掘算法(backbone network mining algorithm based on minimum critical dominating structure, BNMA)。运用提出的基于最小关键支配结构的关键边度量，识别电力光缆网的关键边，进而挖掘出电力光缆网中关键节点实体，获取满足连通约束的最小规模电力光缆网骨干网络，算法具体流程如图3所示。

图3 基于最小关键支配结构的电力光缆网骨干网络挖掘算法流程

算法的具体步骤如下：

4 实例分析

以吉林省的省级电力光缆网的物理拓扑结构和南部电力光缆网的物理拓扑结构为基础进行算法实例分析，运用本文设计的骨干网络挖掘算法 (BNMA)与最小连通支配集挖掘方法(the minimum connected dominating set, MCDS)[17]和边介数最小生成树挖掘方法(betweenness and the minimum spanning tree, BMST)[16]对骨干网络挖掘结果进行对比分析。

图4 使用BNMA的南部网骨干网络挖掘结果

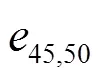
运用骨干网络挖掘算法BNMA、MCDS和BMST，得到南部电力光缆网骨干网络挖掘结果，如表1所示。

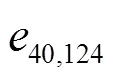
表1 3种方法骨干网络结果比较

图5 BNMA方法的省级电力光缆网骨干网络挖掘结果

5 实验

使用吉林省省级电力光缆网的物理拓扑结构和南部电力光缆网的物理拓扑结构，设计两组实验，分别使用BNMA、MCDS、BMST挖掘骨干网络，并据此模拟蓄意攻击电力光缆网表示模型，通过对比分析网络连通性[23]的变化趋势，验证BNMA的有效性。

依据MCDS、BMST、BNMA挖掘出的南部电力光缆网的骨干网络，依次移除其骨干网络的骨干边集，网络连通性的下降趋势如图6所示。

图6 移除骨干网络过程南部电力光缆网的连通性下降趋势

在移除BNMA挖掘的骨干网络中骨干边集的第1条边和第2条边后，连通性下降37%，这2条边都被移除后，南部电力光缆网表示模型被分成2个独立的子网络，如图7所示。对于BNMA，在被移除前4条边后，电力光缆网表示模型被分成3个独立的子网络，连通性下降56%，而BMST、MCDS未导致连通未发生变化。在BMST、MCDS分别被移除前8条边、前19条边后，连通性分别下降37%、56%。在移除全部的骨干边集后，BNMA、BMST、MCDS连通性分别下降63%、64%、49%，平均连通性下降率分别为2.25%、1.9%、1.8%。与其他两个方法相比，BNMA的平均连通性下降率分别提高0.35%、0.45%。由此说明BNMA可有效挖掘南部电力光缆网的骨干网络。

依据MCDS、BMST、BNMA挖掘出的省级电力光缆网骨干网络，依次移除其骨干网络中的骨干边集，网络连通性的下降趋势如图8所示。在图8中，BNMA的骨干网络由86条边构成，MCDS的骨干网络由84条边构成，而BMST方法的骨干网络由92条边构成。3种方法的网络连通性均呈下降趋势，当依次移除BNMA挖掘的骨干网络中骨干边集的前8条边后，连通性下降14%。当移除BMST方法骨干边集中的前25条边后，连通性下降10.72%。在依次移除MCDS的前18条边后，连通性下降9.96%。说明BNMA首先挖掘到电力光缆网络中的关键实体。当骨干网络全部移除，BNMA、MCDS、BMST连通性分别下降60%、62%、85%。因为BMST的骨干网络包含的边数较多(92条)，故连通性下降也最多，但构成的骨干网络边数目过多，不符合骨干网络最小规模约束条件。由此，BNMA可有效挖掘出省级电力光缆网的骨干网络。

图7 南部电力光缆网骨干网络前2条边被移除

图8 移除骨干网络过程省级电力光缆网的连通性下降趋势

6 结语

本文设计了一种基于最小关键支配结构的电力光缆网骨干网络挖掘算法。根据吉林省省级电力光缆网的物理拓扑结构和南部电力光缆网的物理拓扑结构，设计两组实验，分别使用BNMA、MCDS、BMST挖掘的骨干网络模拟蓄意攻击电力光缆网表示模型，通过对比分析网络连通性的变化趋势，验证所提BNMA的有效性。根据实验分析结果，随着移除吉林省南部电力光缆网表示模型中的骨干网络，与MCDS、BMST相比，南部网连通性平均下降率分别提高0.35%、0.45%。在省级电力光缆网表示模型中，BNMA可挖掘到电力光缆网络中的关键实体，并能有效挖掘电力光缆网络中的骨干网络。

[1] 陈刚, 王肖珊. 区域电力通信网光缆智能分配监测系统的设计与实现[J]. 现代电子技术, 2017, 40(9): 166-168.

CHEN Gang, WANG Xiaoshan. Design and implementation of optical cable intelligent distribution monitoring system for regional electric power communication network[J]. Modern Electronic Technology, 2017, 40(9): 166-168.

[2] 周冬玥, 胡福年, 陈军. 基于复杂网络的电力系统鲁棒性分析[J]. 电力系统保护与控制, 2021, 49(1): 72-80.

ZHOU Dongyue, HU Funian, CHEN Jun. Robustness analysis of power system based on a complex network[J]. Power System Protection and Control, 2021, 49(1): 72-80.

[3] 夏正云, 陈殿欣, 韦磊, 等. 南京市电力光纤传输网拓扑分析与研究[J]. 电气自动化, 2016, 38(3): 60-63.

XIA Zhengyun, CHEN Dianxin, WEI Lei, et al. Topology analysis and research on the power fiber transmission network in Nanjing[J]. Power System & Automation, 2016, 38(3): 60-63.

[4] 刘涤尘, 冀星沛, 王波, 等. 基于复杂网络理论的电力通信网拓扑脆弱性分析及对策[J]. 电网技术, 2015, 39(12): 325-331.

LIU Dichen, JI Xingpei, WANG Bo, et al. Topological vulnerability analysis and countermeasures of electrical communication network based on complex network theory[J]. Power System Technology, 2015, 39(12): 325-331.

[5] 李彬, 卢超, 景栋盛, 等. 负载与风险联合均衡的电力通信网路由优化算法[J]. 中国电机工程学报, 2019, 39(9): 2713-2722.

LI Bin, LU Chao, JING Dongsheng, et al. Optimized routing algorithm with load and risk joint balance in electric communication network[J]. Proceedings of the CSEE, 2019, 39(9): 2713-2722.

[6] 林潇, 刘洋, 许立雄, 等. 基于系统生存性的骨干网架搜索方法[J]. 电测与仪表, 2019, 56(12): 49-56.

LIN Xiao, LIU Yang, XU Lixiong, et al. A method of searching backbone grid based on survivability of power system[J]. Electrical Measurement & Instrumentation, 2019, 56(12): 49-56.

[7] 贾惠彬, 盖永贺, 李保罡, 等. 基于强化学习的电力通信网故障恢复方法[J]. 中国电力, 2020, 53(6): 34-40.

JIA Huibin, GAI Yonghe, LI Baogang, et al. Power communication network recovery from large-scale failures based on reinforcement learning[J]. Electric Power, 2020, 53(6): 34-40.

[8] 孙继泽, 杜金其, 王伟, 等. 电力光纤通信网络实时安全风险量化参数优化算法[J]. 激光杂志, 2021, 42(12): 176-180.

SUN Jize, DU Jinqi, WANG Wei, et al. Real time security risk quantification parameter optimization algorithm for power optical fiber communication network[J]. Laser Journal, 2021, 42(12): 176-180.

[9] 文劲宇, 周博, 魏利屾. 中国未来电力系统储电网初探[J]. 电力系统保护与控制, 2022, 50(7): 1-10.

WEN Jinyu, ZHOU Bo, WEI Lishen. Preliminary study on an energy storage grid for future power system in China[J]. Power System Protection and Control, 2022, 50(7): 1-10.

[10]张磊, 纪春华, 王旭蕊, 等. 基于最小路径选择度的电力通信网络路由优化策略研究[J]. 电力系统保护与控制, 2022, 50(1): 141-147.

ZHANG Lei, JI Chunhua, WANG Xurui, et al. A routing optimization strategy for an electric power communication network based on the minimum path selectivity degree[J]. Power System Protection and Control, 2022, 50(1): 141-147.

[11] 杜俊渭, 张瑞强, 戴睿, 等. 骨干电力通信网中波分复用网络的可靠性评估[J]. 光通信技术, 2015, 39(6): 9-12.

DU Junwei, ZHANG Ruiqiang, DAI Rui, et al. Reliability evaluation of WDM networks in the backbone electric power communication network[J]. Optical Communication Technology, 2015, 39(6): 9-12.

[12] 汪凯, 吴军, 刘涤尘. 基于需求差异化的电网核心骨干网架构建[J]. 电测与仪表, 2018, 55(2): 25-32.

WANG Kai, WU Jun, LIU Dichen, et al. Construction of the core backbone of network based on the needs differentiation[J]. Electrical Measurement & Instrumentation, 2018, 55(2): 25-32.

[13] 李佳威, 吴明功, 温祥西, 等. 基于最小连通支配集的复杂网络关键节点与连边识别方法[J]. 系统工程与电子技术, 2019, 41(11): 2541-2549.

LI Jiawei, WU Minggong, WEN Xiangxi, et al. Identifying key nodes and edges of complex networks based on the minimum connected dominating set[J]. Systems Engineering and Electronics, 2019, 41(11): 2541-2549.

[14] PARTHIBAN N, RAJASINGH I, RAJAN R S. Minimum connected dominating set for certain circulant networks[J]. Procedia Computer Science, 2015, 57: 587-591.

[15] LUO Y, WU J. Linking the minimum spanning tree and edge betweenness to understand arterial corridors in an ecological network[J]. Landscape Ecology, 2021: 1-17.

[16] SUN P G, MA X, CHI J. Dominating complex networks by identifying minimum skeletons[J]. Chaos Solitons & Fractals, 2017, 104: 182-191.

[17] 何玉钧, 高晗星, 周生平. 骨干光通信网链路重要度识别方法研究[J]. 光通信研究, 2018(6): 56-60.

HE Yujun, GAO Hanxing, ZHOU Shengping. Reliability evaluation of WDM networks in the backbone electric power communication network[J]. Research on Optical Communication, 2018(6): 56-60.

[18] 刘垒, 谭阳红, 金家瑶, 等. 电力通信网的关键节点辨识[J]. 电力系统及其自动化学报, 2020, 32(2): 28-34.

LIU Lei, TAN Yanghong, JIN Jiayao, et al. Key node identification of power communication network[J]. Proceedings of the CUS-EPSA, 2020, 32(2): 28-34.

[19] 樊冰, 郑陈熹, 唐良瑞, 等. 基于多属性决策的电力通信网的节点重要度计算方法[J]. 电力系统保护与控制, 2020, 48(9): 68-76.

FAN Bing, ZHENG Chenxi, TANG Liangrui, et al. Node importance evaluation method of electric power communication network based on multi-attributes decision making[J]. Power System Protection and Control, 2020, 48(9): 68-76.

[20] MATHEBULA V C, SAHA A K. Reliability of IEC 61850 based substation communication network architecture considering quality of repairs and common cause failures[J]. Protection and Control of Modern Power Systems, 2022, 7(1): 174-188.

[21] 马庆峰, 王庭钧, 单丽, 等. 基于业务链路的电力通信网络可靠性评估模型[J]. 数学的实践与认识, 2019, 49(19): 207-215.

MA Qingfeng, WANG Tingjun, SHAN Li, et al. Reliability evaluation model of electric power communication network based on business link[J]. Mathematics in Practice and Theory, 2019, 49(19): 207-215.

[22] JIANG W C, LIU Y H, WANG S D, et al. Bridge-edges mining in complex power optical cable network based on minimum connected chain attenuation topological potential[J]. KSII Transactions on Internet and Information Systems, 2021, 15(3): 1030-1050.

[23] LIU J, XIONG Q, SHI W. Evaluating the importance of nodes in complex networks[J]. Physica A: Statistical Mechanics and Its Applications, 2016, 452: 209-219.

Backbone network mining algorithm in a power optical cable network based on minimum critical dominating structure

JIANG Wanchang1, 2, LIU Yanhui1, 2, GUO Jian3, WANG Shengda4, LIU Danni4

(1. School of Computer Science, Northeast Electric Power University, Jilin 132012, China; 2. Northeast Electric Power University, Jilin Smart Grid Information Technology Engineering Laboratory, Jilin 132012, China; 3. Fengman Power Distribution Construction Office of Jidian Group Co., Ltd., Jilin 132000, China; 4. Jilin Information & Telecommunication Company, Jilin Electric Power Corporation Ltd., Jilin 130021, China)

The minimum scale backbone network frame of power optical cable network contains important communication and hub stations, bridge links and other key entities, and meets the requirements of connectivity constraints. To mine the backbone network of the power optical cable network, a network mining algorithm based on minimum critical dominating structure is proposed. First, according to the physical topology of a provincial power optical cable network, a representative model of the power optical cable network is constructed. Second, to identify the critical edge of network, a measurement method of critical edge is proposed based on the minimum critical dominating structure. Finally,an algorithm based on the minimum critical dominating structure is designed to realize the mining of the backbone network. Two groups of experiments are designed using the provincial and the southern power optical cable networks in Jilin Province. The algorithm and two classical methods are used to mine the backbone network. Based on this, a deliberate attack is simulated on the power optical cable network, and the change trend of network connectivity is compared and analyzed to verify the effectiveness of the algorithm.

minimum critical dominating structure; complex network; power optical cable network; backbone network

10.19783/j.cnki.pspc.220291

吉林省教育厅科学技术研究项目资助(JJKH 20220111KJ)；吉林省科技发展计划项目资助(20210203044SF)

This work is supported by the Sci & Tech Research Project of Jilin Education Department (No. JJKH 20220111KJ).

2022-03-08；

2022-05-23

姜万昌(1983—)，男，博士，副教授，硕士生导师，研究方向为复杂网络与大数据、电力光纤网监测与分析、软件网络等；E-mail:jwchang84@163.com

刘艳辉(1995—)，女，硕士，研究方向为复杂网络、电力光纤网络；E-mail: 1369442677@qq.com

郭 健(1976—)，男，学士，研究方向为光纤通信网络。E-mail: 1680801@qq.com

(编辑 姜新丽)