基于深度强化学习的含高比例可再生能源配电网就地分散式电压管控方法

徐博涵，向 月，潘 力，方梦秋，彭光博，刘友波，刘俊勇

基于深度强化学习的含高比例可再生能源配电网就地分散式电压管控方法

徐博涵，向 月，潘 力，方梦秋，彭光博，刘友波，刘俊勇

(四川大学电气工程学院，四川 成都 610065)

含有可再生能源并网的区域电网存在通信条件差、量测设备不足、不同节点的电压管控设备难以协同等问题，因此提出一种基于深度强化学习的分散式就地电压管控方法。该方法首先将缺少量测数据的电压管控问题转化为部分可观的马尔科夫决策问题，构建了以网络损耗最小为优化目标的多智能体分散式电压管控框架。然后采用多智能体深度确定性策略梯度算法对智能体进行离线训练，并使用训练完成的智能体进行在线电压管控。最后，基于改进的IEEE33节点系统进行了算例仿真和分析。结果表明，各智能体可以根据各自节点的电气信息求解出近似的全局最优解。

多智能体；电压管控；量测数据不足；多智能体深度确定性策略梯度算法

0 引言

近年来，为了应对环境问题，世界各国都在推动能源系统的低碳化、清洁化转型。在此背景下，我国提出了“双碳”要求，力争在2030年前实现碳达峰，在2060年前实现碳中和[1]。在电力行业，由于风电和光伏等新型可再生能源在发电过程中有着零碳排放和零边际成本等优点，其发电占比正在快速上升[2]。但是，随着可再生能源装机容量的增大，电网的电压波动变得更为剧烈，无功电压补偿技术成为了一种重要的电压管控手段[3]。由于大多数可再生能源发电都是通过逆变器进行并网的，具有利用空闲容量提供无功补偿的能力，探索可再生能源发电的无功管控方法对加强电网电压管控能力具有现实意义[4]。

目前电压管控领域的研究方向主要分为集中式电压管控、分布式电压管控以及就地电压管控3种。集中式管控通过设置一个中心处理器，来接收整个电网的全部信息，作出全局最优决策。文献[5]基于动态规划法实现了SVC设备的无功电压管控，文献[6-7]基于混合整数二阶锥规划法实现了SVC和投切电容器的协同电压管控。文献[8]基于粒子群算法实现了无功电压管控，具有更强的全局寻优能力。文献[9]基于鲁棒算法实现了考虑不确定性辐射状配电网的电压管控。但是集中式电压管控方法都需要良好的通信条件，而且中心处理器面临着巨大的计算压力。

为了解决上述问题，国内外学者对基于数据驱动的电压管控技术进行了大量研究，并取得了初步成果。文献[14]基于深度确定性策略梯度算法进行电压管控，实现了基于数据的离线算法训练，求解速度较基于模型求解的算法有大幅的提升。为了增强算法的鲁棒性，文献[15]采用多智能体算法设置多个智能体分别对电网各个区域进行电压管控，实现了基于数据的分布式管控。但是，该方法依然需要完备的系统观测数据。为此，文献[16]提出了一种基于双层深度确定性策略梯度算法的电压管控方法，训练两种智能体来分别完成目标电压设置和目标电压逼近的任务，实现了在少量量测数据下的无功电压管控。文献[17]提出使用卷积神经网络拟合潮流无功优化函数，实现了低感知态势下含高比例清洁能源的电压管控，但是上述方法依然无法摆脱对通信条件的依赖。

基于上述研究现状，本文设计了一种基于深度强化学习的含高比例可再生能源配电网就地分散式电压管控。首先建立了可再生能源并网的电压管控机理模型，为智能体提供交互环境。然后，将电压管控问题转化为部分可观的马尔科夫决策过程(partially observable markov decision process, POMDP)，构建了智能体的观测空间、动作空间以及回报函数，引导各智能体协同进行电压管控，降低网络损耗，并防止电压越界。之后，使用多智能体深度确定性策略梯度(multi-agent deep deterministic policy gradient, MADDPG)算法对多智能体进行训练，实现了各智能体间决策的协同进化，训练完成的智能体在进行决策时可以计及其他智能体决策的耦合影响，具有更好的决策稳定性。最后，使用改进的IEEE33节点系统进行算例仿真和分析，验证了本文所提管控方法的有效性。

1 电压管控机理模型

本节首先对电压协同控制框架中的可再生能源设备进行建模，基于不同设备的无功补偿特性定义其运行区间，然后给出了潮流模型，用于下文的智能体训练过程。

1.1 风电出力模型

文献[18]表明风速服从韦伯分布，因此可以使用式(1)来表示风电机组的有功功率。同时，风电机组一般配备有连续的无功补偿装备[19]，所以风电机组的实际无功功率可以用式(2)表示。

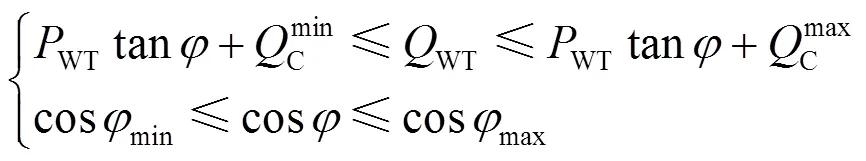
1.2 光伏出力模型

文献[20]表明光照强度服从贝塔分布，因此可以使用式(3)来表示光伏电源的有功功率。

同时，根据文献[21]的研究表明，光伏电源可以通过逆变器优化(optimal inverter dispatch, OID)策略来控制光伏电源输出的无功功率，使用OID策略的光伏电源运行区间可表示为

1.3 负荷的不确定模型

文献[22]表明可以使用正态分布来表示负荷的不确定性，如式(5)—式(8)所示。

1.4 潮流模型

本文仅考虑稳态下的电压管控，潮流模型如式(9)—式(11)所示。

同时，由功率守恒定理可得

2 量测数据不足下的多智能体电压管控模型

本节首先对智能体模型中涉及的马尔科夫决策过程进行介绍，然后将多智能体就地分散式电压管控问题转化为POMDP问题，建立了多智能体电压管控模型。

2.1 马尔科夫决策过程

在机器学习领域中，一般采用马尔科夫决策过程来描述智能体与环境的交互过程。在一个马尔科夫决策过程中，智能体可以从外界环境中获取观测数据，并使用自身策略来根据观测数据作出决策。受到决策动作的逆向影响，环境状态发生更新，智能体根据新的环境状态获取回报，并开始新一轮的马尔科夫决策过程。马尔科夫决策过程的流程图如图1所示。

图1 马尔科夫决策过程流程图

多智能体马尔科夫决策过程的全部信息可以整合为一个元组，如式(13)所示。

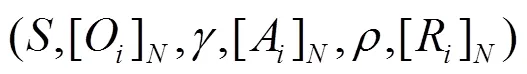
在多次的马尔科夫决策过程中，智能体使用值来表示自己当前动作获取的总收益期望，并以最大化值为目标来更新自身的策略函数。

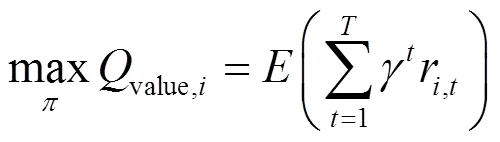
2.2 基于POMDP的多智能体电压管控模型

本节将量测数据不足下的电压协同管控问题转化为POMDP问题，对其环境状态空间、观测空间、动作空间和回报函数进行定义，引导多智能体根据少量观测数据控制分布式电源协同进行电压管控。

2.2.1环境状态空间

电压管控问题的物理环境为网络潮流，所以智能体的环境状态空间应包含潮流计算所需要的全部信息，如式(18)所示。

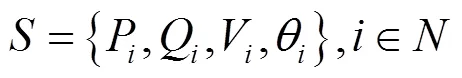
2.2.2观测空间

由于本文考虑的是分散就地电压管控，各智能体仅根据各自管控的可再生能源设备接入节点的电气信息(节点电压及有功、无功功率)进行决策，因此设计智能体的观测空间如式(19)所示。

2.2.3动作空间

动作空间为电压管控问题中智能体可以控制的设备变量，本文为可再生能源设备发电的无功功率。同时，为了满足式(2)和式(4)的无功功率上下限约束，本文使用tanh函数作为神经网络的激活函数，将神经网络的输出限制在[-1,1]，并线性放缩至设备的无功功率限制内，如式(20)所示。

2.2.4回报函数

由于智能体会以最大化获得回报为导向来更新策略函数，因此设计如式(21)的回报函数，引导智能体降低网络损耗并防止电压越限。

图2 多智能体电压管控POMDP框架

3 基于MADDPG的多智能决策算法

3.1 多智能体的集中式离线训练

MADDPG算法是一种新兴的基于多智能体Actor-Critic网络的深度强化学习算法。它引入了双层多智能体Actor-Critic网络的概念，在智能体进行集中式训练前复制一份初始的多智能体Actor-Critic网络作为目标网络，并使用软更新技术对双层网络的参数进行异步更新，大幅度提升了多智能体训练的速度和稳定性[23]。MADDPG算法的流程图如图3所示。

3.1.1 Actor神经网络迭代过程

图3 MADDPG算法流程图

Actor神经网络参数的更新梯度由Critic神经网络计算的值决定，并根据预设的更新系数进行更新，可表示为

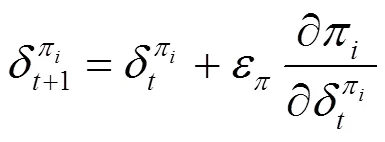
3.1.2 Critic网络迭代过程

MADDPG算法根据贝尔曼公式构建了Critic网络参数的误差函数，为Critic网络参数提供了更新梯度，计算公式为

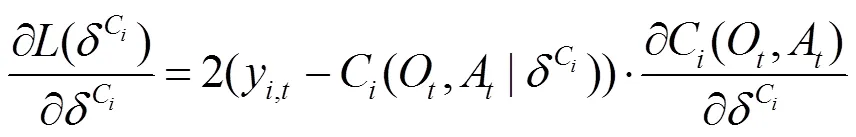
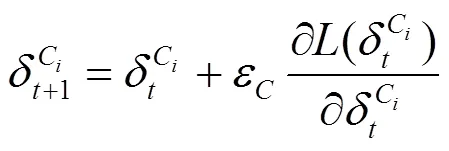
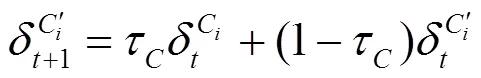
此外，MADDPG算法设置了经验池来消除训练数据的关联性，进一步提高算法性能。算法的详细流程如表1的伪代码所示，表中为训练总次数，为智能体总数，为采样数量。

表1 MADDPG算法伪代码

3.2 多智能体的在线分布式决策

多智能体的集中式训练过程已经离线完成了MADDPG算法中Actor网络参数的迭代，在线运行时智能体可以直接使用迭代完成的网络参数生成策略函数进行独立决策，不再需要同其他智能体进行信息交流，消除了对通信条件的依赖，决策过程如式(32)所示。

4 算例仿真与分析

本节基于改进的IEEE33节点系统[24]进行算例仿真与分析，系统结构如图4所示。系统加入5个分布式光伏电源以及2个风电机组，并且仅在可再生能源接入节点设置了量测设备，智能体仅根据各自接入节点的电气信息对可再生能源设备的无功功率进行控制，可再生能源设备参数如表2所示。

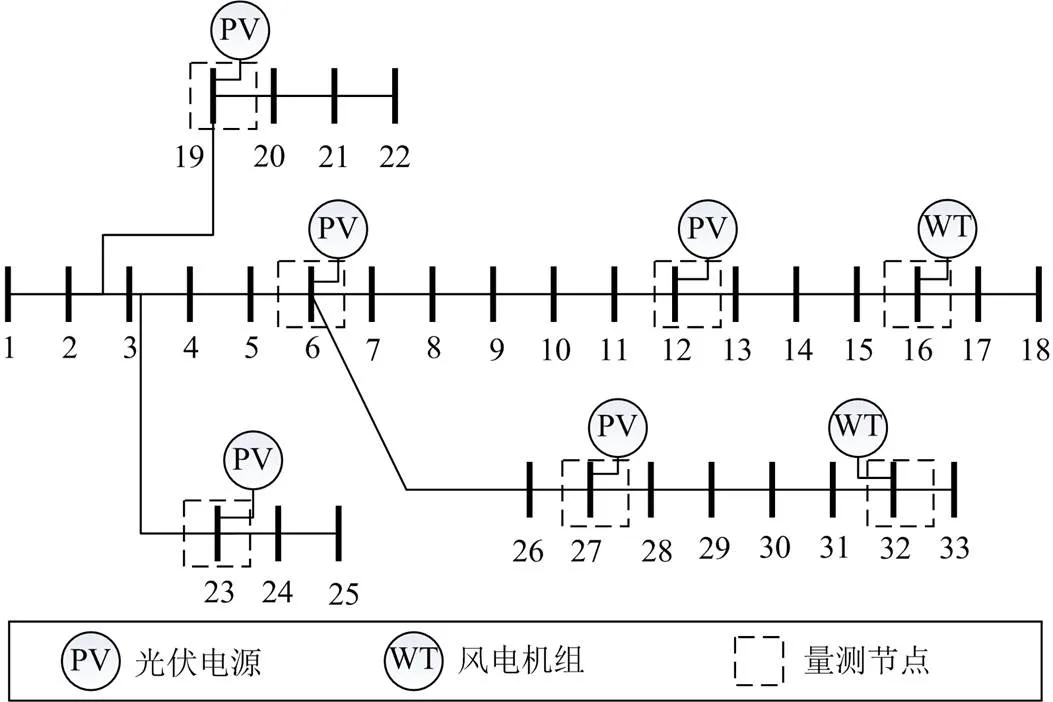
图4 改进IEEE33节点系统结构

表2 设备参数

4.1 智能体训练结果分析

基于第1节的电压管控机理模型随机生成60天的运行场景，并采用MADDPG算法为可再生能源接入节点训练智能体，算法所设定的超参数如表3所示。

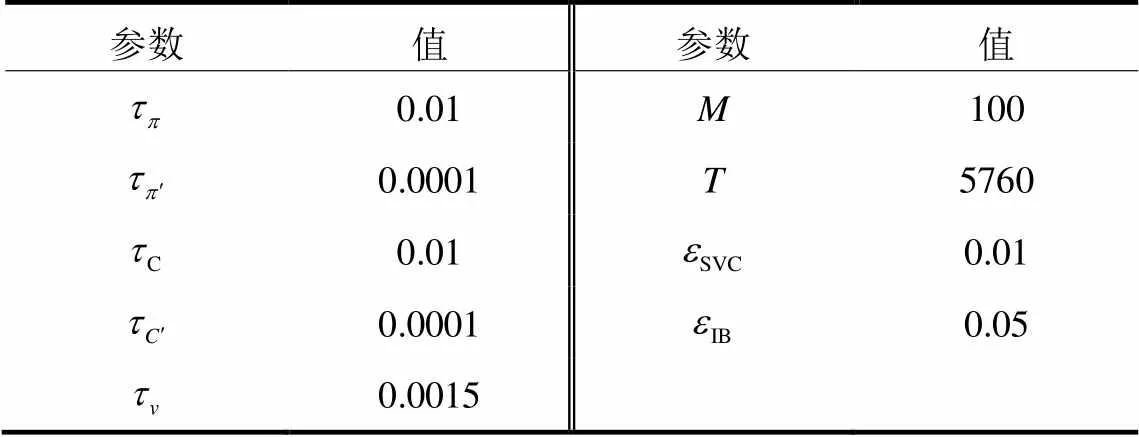
表3 MADDPG算法超参数

图5为训练过程中各智能体的回报值，由于6、19、23、27号节点位于线路首端，不存在电压越限现象，因此具有相同的回报曲线。从回报曲线可以看出，在前10个训练周期内智能体还在进行随机探索，获取的回报很少。在第10—第30周期，智能体开始根据探索得到的经验更新自己的策略，回报曲线快速上升，只有12、16、32号节点偶尔会有轻微的电压越限，导致回报函数略微降低。而第30个周期以后，各智能体已经具有一致的回报函数，且回报函数逐渐收敛，说明各节点已经学习到降低网损的最优策略，并且不再出现电压越限现象。

图5 智能体训练平均回报曲线

随机生成2000次电网运行场景对训练完成的智能体的有效性进行验证。在2000次场景中，各节点的波动区间如图6所示，当无电压管控时，电网电压的波动剧烈，多个节点存在电压越限现象，以可再生能源接入节点最为严重。而在智能体进行电压管控后，电网整体的电压质量得到明显改善，已经不存在电压越界现象，各节点电压的波动区间普遍收紧，最大电压偏差由0.1 p.u.降低至本文预设的0.07 p.u.以内，证明了本文所提管控方法在电压管控方面的有效性。值得注意的是，部分节点出现了最大电压上升的现象，这是因为智能体在控制电压的同时要降低电网损耗，因此在允许的电压波动范围内进行了无功补偿。

图6 管控电压波动区间对比

4.2 电压管控性能分析

由于本文所提算法考虑的是量测设备不足、缺乏可靠通信条件的区域配电网的无功电压管控问题，在传统的电压控制策略中，只有分散式就地控制策略可以有效运行[17]。因此，选择()下垂控制策略进行算例对比，验证本文所提方法在控制电压和降低网损方面的有效性。

给定系统一天内的总负荷和可再生能源的总输出功率，如图7所示[25]。选取电压波动最为明显的末端可再生能源接入节点(12、16、32号节点)进行电压分析，不同控制策略下各节点的电压如图8所示。可以看到，两种控制方式下，各节点的电压波动均得到了有效抑制，不再出现电压越限问题，但是相较于下垂控制，本文所提方法在不同节点会适应性地调整节点所维持的电压等级，这主要是因为在本文设定的回报函数下，智能体只有在控制电压水平的同时尽量降低网络损耗，才可以获得最大回报。

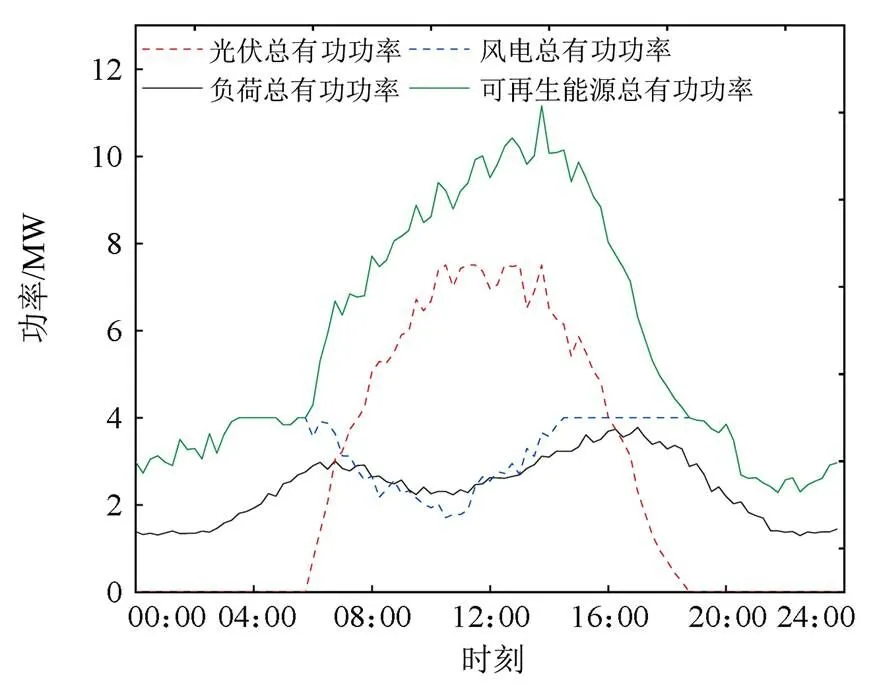
图7 IEEE33节点系统的日运行数据

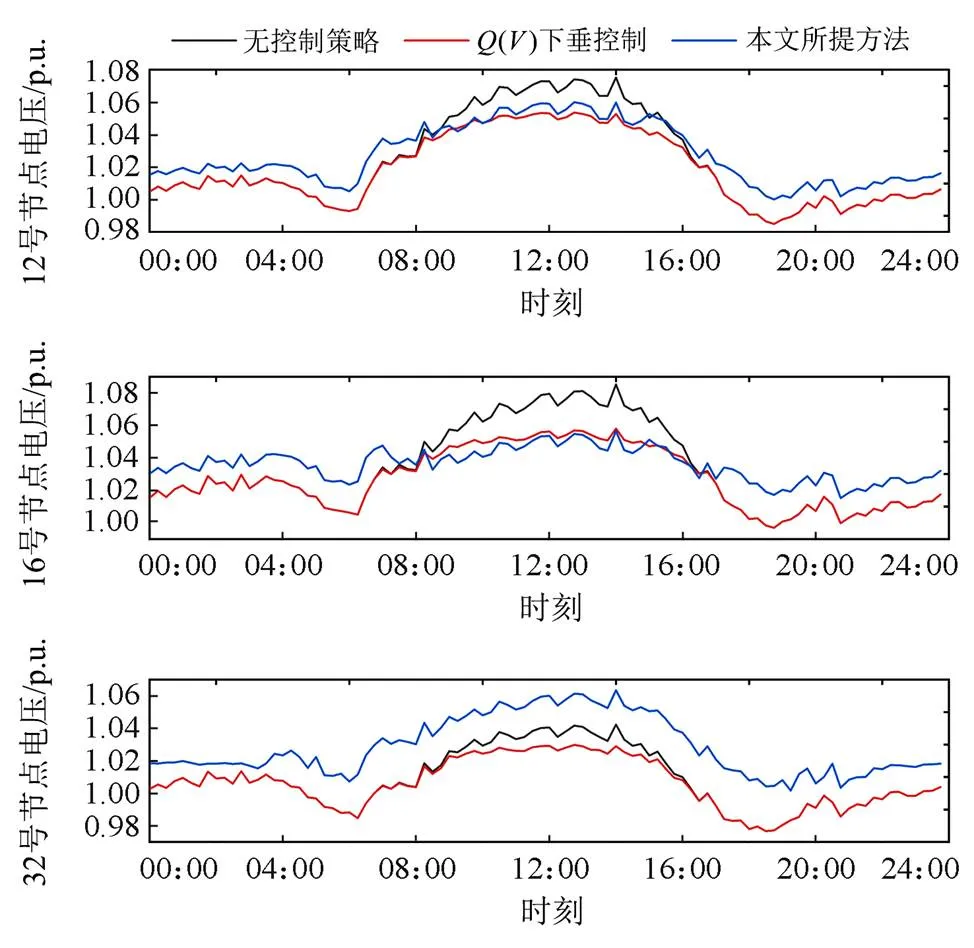
图8 日运行状态下的电压

图9给出了4种控制方法下一天内的网络损耗，其中，集中式控制使用完备的全局信息，可以认为是最优决策，而()下垂控制和本文所提方法均只使用本地观测信息。从图9中可以看出，由于在08：00以前和18：00以后，光伏电源出力较少，电网电压偏移量不大，在此情况下，()下垂控制几乎不动作，电网损耗持平。而本文方法则会在电压允许范围内进行无功补偿以降低电网损耗，同时由于电网的安全压力较小，智能体专注于降低网损，几乎可以达到与集中式管控方法相近的精度。而在10：00—16：00，光伏出力大幅增加，电网电压偏移量增大，()下垂控制为了控制节点电压开始吸收无功功率，但是各节点之间难以有效配合，因此出现了吸收无功功率过多、电网损耗增大的现象。相比之下，本文所提方法中各智能体的策略在训练过程中是协同进化的，各智能体会在保证不出现电压越界的前提下，合作降低网络损耗。但是此时电网的安全压力较大，由于各智能体仅可以使用本地信息进行决策，因此决策动作会较为保守，相较于集中式控制方法网络损耗略微增大。最终，本文管控方式下各可再生能源设备发出的无功功率如图10所示。

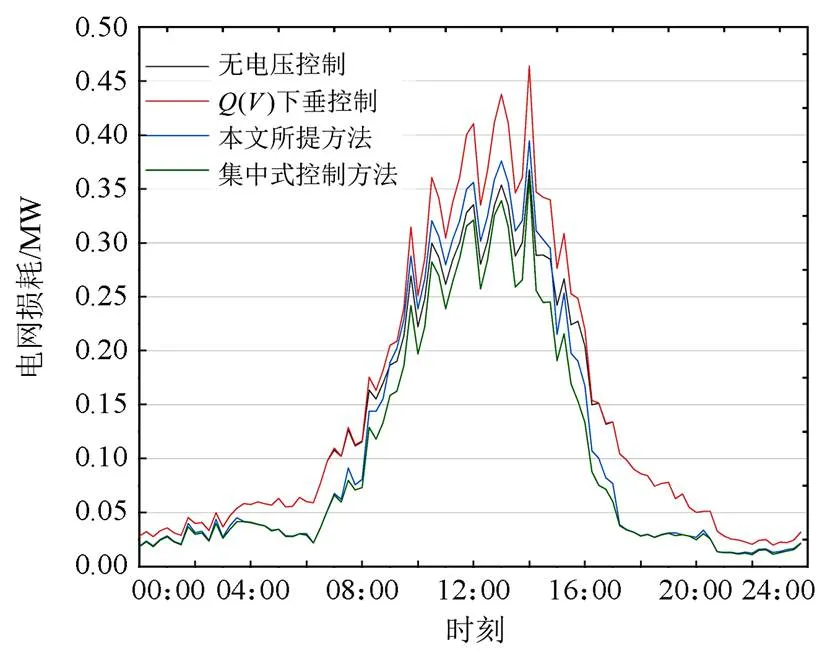
图9 日运行状态下的网络损耗

为了进一步对本文所提方法的设备协同管控性能进行分析，给出了14：00时3种控制方法下各可再生能源接入节点的无功功率，如表4所示。可以看到，()下垂控制仅可以根据节点电压偏移量线性地进行无功补偿，而本文所提方法中各节点的无功功率与集中式控制方法具有一致的方向，证明各个智能体间可以协同完成降低网络损耗和平抑电压波动的任务，而不是单纯地降低本地节点的电压偏差量。如32号节点的智能体会在安全范围内发出无功功率来降低网络损耗，而不是根据电压偏移量来吸收无功功率。从数值上来看，相较于集中式管控，本文方法的无功补偿功率偏大，主要是因为智能体在无法获得其他智能体信息的情况下，会更加倾向于适量地进行过量补偿，以增加少量的网络损耗为代价，来保证节点电压不发生越限。

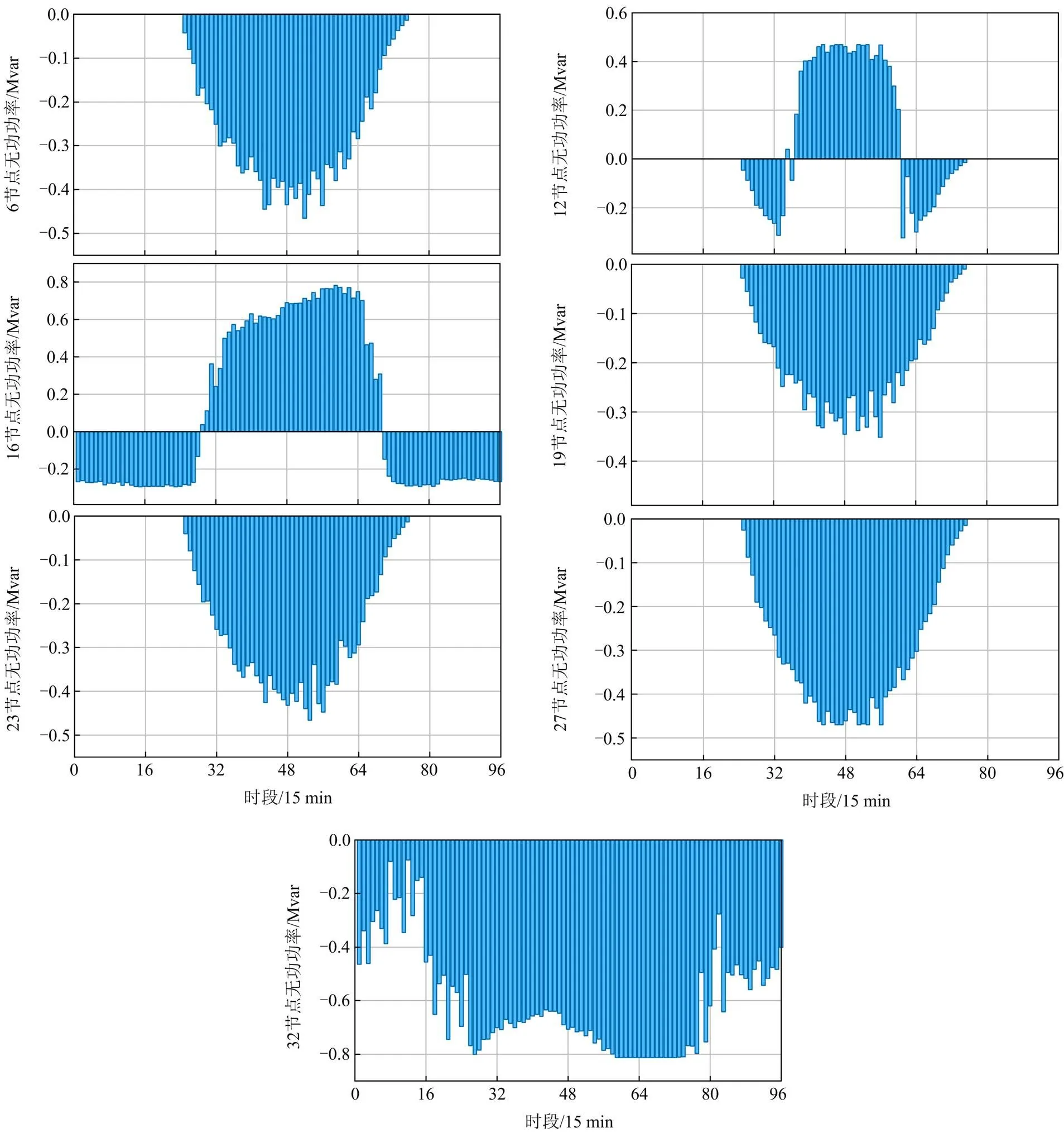
图10 可再生能源发电的无功功率

表4 可再生能源发电无功功率对比

最终，本文所提方法、无管控方法、()下垂控制和集中式控制一天内的总网络损耗分别为2.76 MWh、3.09 MWh、3.48 MWh和2.54 WMh。本文方法相较于()下垂控制，网络损耗下降了20.7%，可以证明本文所提方法具有与()下垂控制相同的电压管控性能的同时，可以大幅降低网络损耗，具备有效性。同时，虽然本文方法较集中式控制方法网络损耗略有增加，但是本文方法本质上是一种就地控制策略，不需要对通信设备和计算中心进行额外投资，因此具有一定的现实意义。

5 结论

本文提出了一种基于多智能体深度确定性梯度算法的多智能体协同电压管控方法，实现了在量测数据不足的情况下不依赖通信的多智能体就地分散式无功电压管控。通过算例分析，证明了本文所提方法中智能体可以根据可再生能源接入节点的电气信息独立进行无功补偿功率决策，有效地抑制电压波动，防止节点电压越限。并与就地控制和集中式控制方法进行了性能对比，本文方法相较于()下垂控制，可以大幅降低电网的网络损耗，具有优越性。相较于集中式控制方法，虽然本文方法的网损略有上升，但是集中式控制方法需要完备的全局信息，在量测数据不足的情况下无法求解，因此文本方法在缺少在线监测设备和可靠通信条件的区域配电网中具有实用性。如何进一步提升智能体的管控精度，将是本文后续研究的重点。

[1] 马国真, 林毓军, 张泽亚, 等. 计及源荷多重不确定性的综合能源系统鲁棒经济调度方法[J]. 电力系统保护与控制, 2021, 49(20): 43-52.

MA Guozhen, LIN Yujun, ZHANG Zeya, et al. A robust economic dispatch method for an integrated energy system considering multiple uncertainties of source and load[J]. Power System Protection and Control, 2021, 49(20): 43-52.

[2] 李政洁, 撖奥洋, 周生奇, 等. 计及综合需求响应的综合能源系统优化调度[J]. 电力系统保护与控制, 2021, 49(21): 36-42.

LI Zhengjie, HAN Aoyang, ZHOU Shengqi, et al. Optimization of an integrated energy system considering integrated demand response[J]. Power System Protection and Control, 2021, 49(21): 36-42.

[3] 闫梦阳, 李华强, 王俊翔, 等. 计及综合需求响应不确定性的园区综合能源系统优化运行模型[J]. 电力系统保护与控制, 2022, 50(2): 163-175.

YAN Mengyang, LI Huaqiang, WANG Junxiang, et al. Optimal operation model of a park integrated energy system considering uncertainty of integrated demand response[J]. Power System Protection and Control, 2022, 50(2): 163-175.

[4] 郑能, 丁晓群, 管志成, 等. 基于场景法的配电网有功–无功协调优化[J]. 电网技术, 2019, 43(5): 1640-1651.

ZHENG Neng, DING Xiaoqun, GUAN Zhicheng, et al. Active reactive power coordination optimization of distribution network based on scenario method[J]. Power System Technology, 2019, 43(5): 1640-1651.

[5] 周晓华, 张银, 刘胜永, 等. 静止无功补偿器新型自适应动态规划电压控制[J]. 电力系统保护与控制, 2018, 46(12): 77-84.

ZHOU Xiaohua, ZHANG Yin, LIU Shengyong, et al. Voltage control of static var compensator based on novel adaptive dynamic programming[J]. Power System Protection and Control, 2018, 46(12): 77-84.

[6] 郭清元, 吴杰康, 莫超, 等. 基于混合整数二阶锥规划的新能源配电网电压无功协同优化模型[J]. 中国电机工程学报, 2018, 38(5): 1385-1396.

GUO Qingyuan, WU Jiekang, MO Chao, et al. A model for multi-objective coordination optimization of voltage and reactive power in distribution networks based on mixed integer second-order cone programming[J]. Proceedings of the CSEE, 2018, 38(5): 1385-1396.

[7] 卢姬, 常俊晓, 张云阁, 等. 考虑DG不确定性的主动配电网两阶段无功机会约束优化方法[J]. 电力系统保护与控制, 2021, 49(21): 28-35.

LU Ji, CHANG Junxiao, ZHANG Yunge, et al. Two stage reactive power chance constrained optimization method for active distribution network considering DG uncertainty[J]. Power System Protection and Control, 2021, 49(21): 28-35.

[8] YOSHIDA H, KAWATA K. A particle swarm optimization for reactive power and voltage control considering voltage security assessment[J]. IEEE Transactions on Power Systems, 2000, 15(4): 1232-1239.

[9] DARATHA N, DAS B, SHARMA J. Robust voltage regulation in unbalanced radial distribution system under uncertainty of distributed generation and loads[J]. International Journal of Electrical Power & Energy Systems, 2015, 73: 516-527.

[10] VACCARO A, ZOBAA A F. Voltage regulation in active networks by distributed and cooperative meta-heuristic optimizers[J]. Electric Power Systems Research, 2013, 99(1): 9-17.

[11] 王庆斌, 刘涌, 杨昀, 等. 含分布式电源的10 kV配电网无功电压控制方法[J]. 电力电容器与无功补偿, 2018, 39(2): 125-130.

WANG Qingbin, LIU Yong, YANG Yun, et al. Reactive power voltage control method for 10 kV distribution network with distributed generation[J]. Power Capacitor & Reactive Power Compensation, 2018, 39(2): 125-130.

[12] 梁俊文, 林舜江, 刘明波. 主动配电网分布式无功优化控制方法[J]. 电网技术, 2018, 42(1): 230-237.

LIANG Junwen, LIN Shunjiang, LIU Mingbo. A method for distributed optimal reactive power control of active distribution network[J]. Power System Technology, 2018, 42(1): 230-237.

[13] 蔡永翔, 唐巍, 徐鸥洋, 等. 含高比例户用光伏的低压配电网电压控制研究综述[J]. 电网技术, 2018, 42(1): 220-229.

CAI Yongxiang, TANG Wei, XU Ouyang, et al. Review of voltage control research in LV distribution network with high proportion of residential PVs[J]. Power System Technology, 2018, 42(1): 220-229.

[14] DUAN J, SHI D, DIAO R, et al. Deep reinforcement learning based autonomous voltage control for power grid operations[J]. IEEE Transactions on Power Systems, 2019, 35(1): 814-817.

[15] WANG S, DUAN J, SHI D, et al. A data-driven multi- agent autonomous voltage control framework using deep reinforcement learning[J]. IEEE Transactions on Power Systems, 2020, 35(6): 4644-4654.

[16] ZHANG X, LIU Y, DUAN J, et al. DDPG-based multi-agent framework for SVC tuning in urban power grid with renewable energy resources[J]. IEEE Transactions on Power Systems, 2021, 36(6): 5465-5475.

[17] 张宇精, 乔颖, 鲁宗相, 等. 含高比例分布式电源接入的低感知度配电网电压控制方法[J]. 电网技术, 2019, 43(5): 1528-1535.

ZHANG Yujing, QIAO Ying, LU Zongxiang, et al. Voltage control for partially visible distribution networks with high DG penetration[J]. Power System Technology, 2019, 43(5): 1528-1535.

[18] HETZER J, YU D C, BHATTARAI K. An economic dispatch model incorporating wind power[J]. IEEE Transactions on Energy Conversion, 2008, 23(2): 603-611.

[19] 周瑜. 计及风电场无功支撑能力的电网无功优化调度研究[D]. 济南: 山东大学, 2021.

ZHOU Yu. Research on optimal reactive power dispatching of power grid considering the reactive power support capacity of wind farm[D]. Jinan: Shandong University, 2021.

[20] ZHANG S, CHENG H, LI K, et al. Multi-objective distributed generation planning in distribution network considering correlations among uncertainties[J]. Applied Energy, 2018, 226: 743-755.

[21] DALL' AN ESE E, DHOPLE S V, JOHNSON B B, et al. Optimal dispatch of residential photovoltaic inverters under forecasting uncertainties[J]. IEEE Journal of Photovoltaics, 2017, 5(1): 350-359.

[22] ZHANG S, CHENG H, ZHANG L, et al. Probabilistic evaluation of available load supply capability for distribution system[J]. IEEE Transactions on Power Systems, 2013, 28(3): 3215-3225.

[23] DESAI J P, MAKWANA V H. A novel out of step relaying algorithm based on wavelet transform and a deep learning machine model[J]. Protection and Control of Modern Power Systems, 2021, 6(4): 500-511.

[24] BARAN M E, WU F F. Network reconfiguration in distribution systems for loss reduction and load balancing[J]. IEEE Transactions on Power Delivery, 1989, 4(2): 1401-1407.

[25] 柴园园, 郭力, 王成山, 等. 含高渗透率光伏的配电网分布式电压控制[J]. 电网技术, 2018, 42(3): 738-746.

CHAI Yuanyuan, GUO Li, WANG Chengshan, et al. Distributed voltage control in distribution networks with high penetration of PV[J]. Power System Technology, 2018, 42(3): 738-746.

Local decentralized voltage management of a distribution network with a high proportion of renewable energy based on deep reinforcement learning

XU Bohan, XIANG Yue, PAN Li, FANG Mengqiu, PENG Guangbo, LIU Youbo, LIU Junyong

(College of Electrical Engineering, Sichuan University, Chengdu 610065, China)

A multi-agent decentralized local voltage control method based on the deep reinforcement learning is proposed. This is needed because there are some problems in the regional grid with renewable energy, such as poor communication conditions, insufficient measurement equipment, and difficult coordination of voltage control equipment at different nodes. First, this method transforms the voltage control problem lacking measurement data into a partial observable Markov decision problem, and a multi-agent decentralized voltage control framework with the optimization goal of minimizing network loss is constructed. Then, a multi-agent deep deterministic policy gradient algorithm is used to train the agents offline, and the trained agents are used for online voltage control. Finally, an example is simulated and analyzed based on the improved IEEE33 bus system. The results show that each agent can solve the approximate global optimal solution according to the electrical information of its own node.

multi-agent; voltage control; insufficient measurement data; multi-agent deep deterministic policy gradient algorithm

10.19783/j.cnki.pspc.220050

国家电网科技项目资助“基于群体智能的能源互联网多源协同运行关键技术研究”(SGTJDK00DWJS2100039)

This work is supported by the Science and Technology Project of State Grid Corporation of China (No. SGTJDK00DWJS2100039).

2022-02-12；

2022-03-31

徐博涵(1996—)，男，硕士研究生，主要研究方向为电力系统智能调度；E-mail: bohanxu_scu@163.com

向 月(1987—)，男，通信作者，副教授，博士，主要研究方向为电力系统智能调度等。E-mail: xiang@scu.edu.cn

(编辑 许 威)