轨撑对轨道力学行为的影响

2022-12-19王建西王晓谦王晓曼

石家庄铁道大学学报(自然科学版) 2022年4期

何淼，王建西，3，王晓谦，郭庆，王晓曼

(1.石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室，河北石家庄 050043；2.石家庄铁道大学道路与铁道工程安全保障省部共建教育部重点实验室，河北石家庄 050043； 3.河北省铁路扣件系统技术创新中心，河北石家庄 050043；4.河北翼辰实业集团股份有限公司，河北石家庄 050043)

经济的高效发展依靠物流的快速运输，铁路运输以运量大、全天候、较为廉价的特点成为货物运输的首选。但由于列车轴重的不断增加以及线路条件的制约，线路上的扣件系统存在弹条扣压力不足、轨距变化较大以及轨道几何形位难以保持的现象。特别是当机车车辆从直线地段转入曲线地段时，钢轨除承受较大的垂向力，还要承受横向水平力，这将造成常规的扣件系统难以抑制钢轨的横向位移，进而使得轨道几何形位发生偏移。这种情况下现场多采用轨撑对钢轨进行限制，使钢轨在服役过程中产生较小的偏移，从而提高轨道的安全性，同时减小养护维修成本。而轨撑采用后对轨道系统力学行为的影响如何，轨撑又是怎样影响钢轨位移这一些系列问题有待研究。

对于钢轨位移的研究方面，刘卫丰等[1]研究发现钢轨轨头的横移是由钢轨平移以及扭转的叠加作用引起的，增加扣件刚度、减小扣件间距、减小扣件阻尼都将使钢轨的位移幅值减小。而在曲线地段，曲线半径对钢轨的竖直位移影响较大，对于横向位移基本无太大影响。马莉等[2]研究表明轨撑的使用，增加了钢轨的横向抗力和抗倾覆能力，减少了线路的日常养护维修工作量。尚红霞等[3]研究表明随着钢轨横向位移和轨下垫板刚度的变化，两侧扣件弹条最大等效应力和扣压力发生明显变化。许勇等[4]通过光学钢轨纵向位移监测设备和磁式钢轨纵向位移监测设备对无缝线路位移情况进行监测，分析得出京沪高铁线路钢轨位移变化较小。Szurgottp[5]基于超弹性理论分析移动荷载对扣件系统轨下橡胶垫板应力和位移的影响，提出了各移动荷载作用下轨下垫板的力学行为。耿世虎等[6]用数值分析和有限元分析的方法对其安装状态进行分析，提出了弹条在最佳预压力25 000 N下不同轨道位移时弹条的应力大小。曾志平[7]在探讨钢轨累计位移和列车制动次数之间的关系时利用电磁中继装置模拟列车负载，并对力、位移进行数据采集，得到轨道纵向累计位移与荷载作用次数呈线性正相关，当荷载作用次数较小时，累积位移增加较快，随着重复荷载次数的增加，两者之间的关系近似服从功率函数分布。而对于实验层面，武汉铁路局信阳工务段发现轨撑的存在提高了钢轨的稳定性，保持钢轨轨距，一定程度上减小了钢轨横向变形和不均匀磨耗[8]。以上研究多是从钢轨位移影响因素出发，尽管有些学者考虑了轨撑的作用，但大多只是探究对钢轨整体位移的影响，并未对增加轨撑之后的钢轨力学行为，特别是钢轨的各部分位移情况以及垫板受力情况做出详细的量化对比。而了解钢轨在服役过程中钢轨各部分位移情况有助于针对性的对扣件系统进行改进，以保证钢轨各部分的协同工作，延长钢轨的服役寿命。

对单节钢轨的扣件系统进行仿真分析，建立有轨撑的扣件系统和无轨撑扣件系统有限元模型，并与钢轨进行组合装配。通过改变荷载垂横比大小来模拟列车在不同曲线半径上受到的垂向力和横向力，对仿真得到数据进行验证，并从位移及应力角度入手对不同荷载垂横比下的钢轨轨头横移、轨底平移、钢轨扭转量、轨下垫板应力等进行量化对比，从而得到轨撑对扣件系统服役过程中的影响。

1 扣件系统有限元模型

有轨撑扣件系统(SYX17型扣件系统)与传统的扣件系统相比是在钢轨的外侧增加轨撑，如图1所示。轨撑背立面与钢轨贴合，从而起到抑制钢轨位移、防止侧倾的作用，轨撑的安装间隔与轨枕安装间隔相同，为0.6 m，即安装1 667组/km。

图1 有轨撑扣件

1.1 扣件系统参数

在扣件系统部件结构中，钢轨采用标准60轨，其弹性模量为2.1×105MPa，泊松比为0.3。

轨下垫板作为钢轨的垫板，起到传力、减振的作用，其弹性模量为8 MPa，泊松比为0.48。

弹条采用朔黄铁路中使用的加强型弹条，弹条直径为14 mm。

扣件弹条是塑性材料，考虑扣件系统间各部件的协同作用，弹条有可能发生局部塑性变形，简单地应用线弹性材料模型不能真实反映弹条的真实受力状态，根据弹条的材质和相关生产工艺，并结合文献[6]、文献[9]、文献[10]选取材料的本构关系为塑性模型，屈服强度σs=1 667 MPa，抗拉强度σb=1 863 MPa，强化模量取0.1E。

1.2 荷载及边界条件

利用绘图软件建立弹条、钢轨、铁垫板、轨撑等部件的等比例模型并按照真实作用关系如图1进行组装。

设置边界条件：将轨枕底部进行约束，同时考虑到模型中扣件系统的各个部件之间、扣件系统与钢轨之间的联结状态，其中钢轨与垫板、垫板与轨枕、弹条与垫板、轨撑与钢轨等之间的相互作用作为面-面接触，接触间的摩擦和运动状态根据库伦摩擦模型确定，摩擦因数参照文献[6]、文献[9]、文献[10]。对于钢轨则约束其纵向位移，保证钢轨的横向及垂向自由度。

轮轨接触可以分为单点接触、两点接触和多点接触；其中直线路段时钢轨与轮对多为单点接触，而在曲线地段多为两点接触和多点接触。仿真中采用两点接触，分别在钢轨轨头顶部和钢轨轨头侧面进行垂向力和横向力的加载。

列车采用重载列车，轴重为25 t，同时考虑列车动载的动态系数[11]，则

Q=αQS

(1)

(2)

式中，α为动载系数；t为无量纲复合因子；φ为无量纲轨道质量参数；v为速度。

根据式(1)、式(2)计算，得到垂向荷载为125 kN。参照扣件试验方法[11]，横向力与垂向力(L/V)比值设置为0.1～0.5,并将有轨撑扣件系统和无轨撑扣件系统按不同垂横比设置10种工况。对于弹条的紧固扭矩则是通过对垫圈施加预压力实现[6]。将螺栓轴力即对垫圈的预压力F0与螺栓的紧固扭矩M建立如下联系

(3)

式中，k为紧固扭矩系数，一般情况下在表面氧化且润滑的条件下为0.2；d为螺栓的公称直径。

预压力F0采用28 000 N，根据式(3)对应实际螺栓紧固扭矩约为135 N·m。

2 模型验证

以垂横比为0.5为例，将仿真得到的钢轨横向位移结果与张永兴等[12]提出考虑钢轨扭转时的钢轨轨头位移理论计算结果以及文献[13]中对朔黄铁路开展轨道结构动力性能测试对扣件保持轨距能力中测得的轨头横移量进行对比分析，如表1所示。

表1 钢轨轨头横移对比 mm

在无轨撑存在的情况下钢轨轨头最大横移量为3.46 mm，由于仿真过程中未考虑相邻扣件对钢轨的约束，超出理论计算结果以及动力学仿真结果约1 mm。而与单节点实验结果[9]相比，模型结果中的轨头横移小于实验结果。可见本文中的模型结果介于理论值和实验值之间，认为仿真结果合理，从而验证模型的正确性。

3 轨道力学行为分析

在对轨道的力学行为分析过程中首先分析的是钢轨，而对钢轨的分析则需从钢轨应力以及钢轨位移2个角度入手。在增设轨撑之后，钢轨的应力分布无太大变化，均在钢轨轨腰、轨底处产生环状应力，从环中心向外应力值逐渐减小，其中钢轨的最大应力可从167.6 MPa降低为117.8 MPa，减小的应力值仅为钢轨屈服强度的9%；而钢轨的位移相对于应力来说变化明显，主要表现为增设轨撑之后钢轨各部分位移如轨头横移、轨底平移、钢轨扭转等有较大幅度的减小，这些位移的减小将大大提高行车的安全性。

另一方面轨撑的增加，将在一定程度上改变扣件系统的传力，特别是改变钢轨的向下传力，轨下垫板作为与钢轨直接接触的部件其应力变化最为明显。

故以下将从钢轨位移以及轨下垫板应力2个角度对增设轨撑后的轨道力学行为进行分析。

3.1 轨头横移

钢轨的轨头横移以钢轨顶面以下1.6 mm处横向位移量为表征依据，其中，规定水平方向上向轨道内侧移动为正，向轨道外侧移动为负。图2为不同荷载垂横比下的钢轨轨头横移量。有轨撑扣件系统中钢轨轨头横向位移在-1.15～0.75 mm 之间，当荷载垂横比为0.25左右时，钢轨的轨头横移量为0 mm。此后随着荷载垂横比的增加，钢轨的轨头横向位移向轨道外侧逐渐增大，当荷载垂横比为0.5时，轨头横移达到-1.15 mm；而在无轨撑扣件系统中的钢轨，在荷载垂横比为0.1时，钢轨出现向轨道内侧的位移，位移量仅为0.1 mm，当荷载垂横比为0.2时，钢轨轨头则向轨道外侧横移0.6 mm。此后钢轨轨头向轨道外侧的横移量随着垂横比的增大而增加，当荷载垂横比为0.5时，轨头横移量达到-3.2 mm。此时轨头横移量为有轨撑状态下钢轨轨头横移量的2.7倍。

图2 不同荷载垂横比下钢轨轨头横移

3.2 轨底平移

轨底平移以钢轨轨底横向位移量为表征依据，其中规定以向轨道内侧移动为正，向轨道外侧移动为负。图3为不同荷载垂横比下的钢轨轨底平移量。有轨撑扣件系统中的钢轨轨底平移量在-0.21～ 0.08 mm之间，平移量变化较小，在垂横比为0.15时，钢轨的轨底平移量为0 mm；而在无轨撑扣件系统中钢轨轨底平移量在-0.13 ～ -1.07 mm之间。当荷载垂横比达到0.4后，钢轨轨底向轨道外侧的平移量陡增，当荷载垂横比为0.5时，无轨撑扣件系统的轨底向轨道外侧的平移量达到-1.07 mm，此时轨底平移量为有轨撑状态下钢轨轨底平移量的5倍左右。显然无轨撑扣件系统在垂横比为0.5时，并不能较好地保持轨距。

图3 不同荷载垂横比下钢轨轨底平移

3.3 垂向位移

垂向位移以钢轨轨底垂直方向的位移量为表征依据，以钢轨垂直向上移动为正，垂直向下移动为负。图4为不同荷载垂横比下的轨底垂向位移量。无轨撑扣件系统中的垂向位移量在-1.25 ～ -1.95 mm之间，且轨底垂向位移量随着荷载垂横比的增大而增加。当荷载垂横比为0.5时，钢轨轨底垂向位移量达到-1.95 mm；而在有轨撑扣件系统中，钢轨的轨底垂向位移量仅在-1.02 ～ -1.28 mm之间。

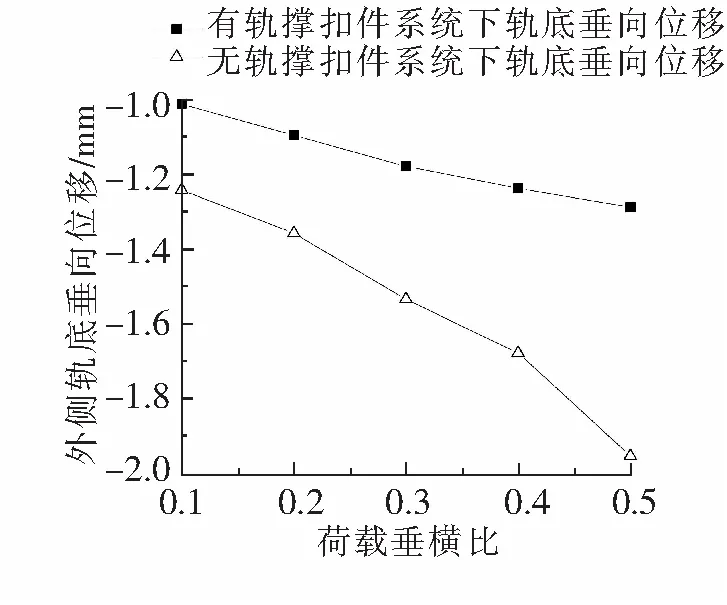
图4 不同荷载垂横比下轨底垂向位移

3.4 钢轨扭转

钢轨扭转量则是以钢轨轨头横移量与钢轨轨底平移量的差值为表征依据，以钢轨向轨道内侧的扭转为正，向轨道外侧的扭转为负。图5为不同荷载垂横比下的钢轨扭转量。有轨撑扣件系统下的钢轨扭转量在-0.93～ 0.72 mm范围内，此种情况下钢轨扭转表现出和钢轨轨头横移类似的现象：在荷载垂横比为0.3以下时，钢轨出现向轨道内侧的扭转。荷载垂横比超过0.3时，钢轨逐渐向轨道外侧扭转。而在无轨撑扣件系统下的钢轨扭转量则在-2.25 ～ 0.31 mm之间，当荷载垂横比为0.15时，钢轨的扭转量接近于0 mm。此后随着荷载垂横比的增加，钢轨向轨道外侧的扭转量逐渐增加，当荷载垂横比到达0.5时，钢轨的扭转量已经达到了-2.25 mm，此时扭转量是无轨撑状态下钢轨扭转量的2.5倍。

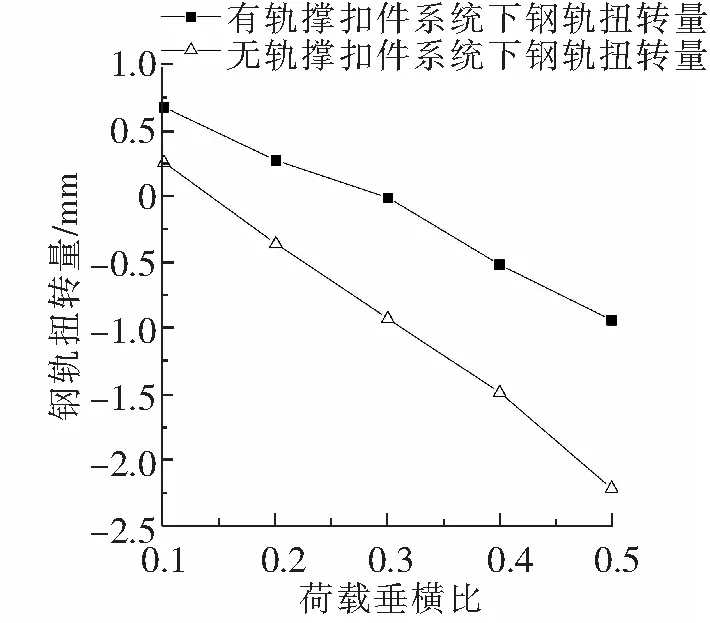
图5 不同荷载垂横比下钢轨扭转

3.5 位移对比

综合来看，在低垂横比下，有轨撑扣件系统中的钢轨无论是轨头横移、轨底平移还是扭转都有向轨道内侧移动的现象。这种现象一方面是由于轨撑的增加，造成了钢轨、弹条以及轨距块之间的直接扣压变成了间接扣压，通过弹条扣压轨距块进而扣压轨撑，最终由轨撑完成对钢轨的扣压，这就造成钢轨内外两侧虽然对弹条的预压力相同，但对钢轨的扣压力却不尽相同，外侧钢轨的扣压力明显会小于内侧，从而出现钢轨在较低垂横比下，向轨道内侧横移、扭转较大的情况；另一方面则是轨撑与钢轨贴合，通过对钢轨的支撑，一定程度上使得钢轨的形心外移，加之荷载的偏心作用，使得其在低垂横比作用下产生向轨道内侧的扭转，并造成钢轨轨头向轨道内侧移动。

图6 不同荷载垂横比下钢轨位移变化量

轨撑的增加有助于减小钢轨各部分位移：如轨撑增加后，当轨头横移量为0时，荷载垂横比由有原来的0.1增大为0.25；钢轨扭转量为0时，荷载垂横比由原来的0.15增大为0.3。为直观反映2种扣件系统下钢轨位移差，绘制图6不同荷载垂横比下钢轨位移变化量。以垂横比0.5为例，轨撑的存在可减小钢轨轨头2.12 mm的横移、减小1.29 mm的扭转，以及0.83 mm的轨底平移。显然轨撑对钢轨位移量影响效果由强到弱依次为轨头横移、钢轨扭转、轨底平移。

4 轨下垫板应力

轨撑的存在改变了轨下垫板的受力情况，现从轨下垫板所受垂向应力和水平应力2个角度进行分析。图7为轨下垫板结构图，其中实线所示方向为纵向，虚线所示方向为横向。由于列车在小半径曲线地段受到较大的横向力，故以垂横比为0.5为例，对垫板横、纵向上的垂向应力及水平应力进行分析。

图7 轨下垫板结构图

图8为垫板横向所受垂向应力图，其中黑色背景线为轨下垫板，空白部分为垫板沟槽。可见轨撑存在时垫板的垂向应力幅值出现不同程度的变化，在垫板的左侧(轨撑侧)垂向应力出现小幅度降低，同一荷载垂横比下应力相差0.5 MPa左右；而在垫板右侧垂向应力有所增长，整体来看垫板的垂向应力幅值减小32.5%。可见，增设轨撑应力值有变化但并未改变垫板应力分布不均匀性。

图8 垫板沿横向上的垂向应力

图9为垫板轨撑侧纵向所受垂向应力，可见无论轨撑是否存在，垫板垂向应力都呈“凹”型分布，即纵向上垫板中部垂向应力大，两侧垂向应力值小。当轨撑存在时，垫板垂向应力值明显减小，特别是轨撑侧垫板中部，最大处垂向应力值减小为无轨撑下的77.7%。

图9 垫板沿纵向上的垂向应力

图10为垫板沿横向所受水平应力图，其中黑色背景线为轨下垫板，空白部分为垫板沟槽。图11为垫板沿纵向所受水平应力图。轨撑存在时，垫板横向上水平应力与垂向应力类似，有轨撑下的垫板应力值9.86 MPa低于无轨撑下的垫板应力值14.57 MPa，应力值减小32.3%。但应力值的减小，并未改变垫板应力分布的非均匀性；纵向上水平应力同样呈“凹”型分布，且有轨撑扣件系统下的轨下垫板水平应力值10.13 MPa低于无轨撑扣件系统下的垫板应力值15.31 MPa，应力值减小34.2%。