均匀流场中圆角方形断面极值风压系数试验研究
2022-12-19高佳文田学东刘小兵
高佳文, 田学东, 杨 群,2,3, 刘小兵,2,3
(1. 石家庄铁道大学 土木工程学院,河北 石家庄 050043;2. 石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室,河北 石家庄 050043;3. 河北省风工程和风能利用工程技术创新中心,河北 石家庄 050043)
0 引言
土木工程中方形断面为最常见的结构形式之一,广泛应用于高层建筑及高耸结构中。作为典型的钝体截面形式,方形断面的气动特性历来备受国内外学者关注。工程结构中通常采用圆角化处理形式来改变方形断面的气动特性,减弱风对结构的作用,保证结构的安全性[1]。
对建筑围护结构进行抗风设计时,通常认为风压信号是符合高斯分布的,然而研究表明,在结构的局部区域,风压信号不再表现为高斯分布,而是表现出明显的非高斯特性,即用传统的假设进行风荷载设计是不合理的[2-3]。已有文献表明[4],非高斯区域的风压时程是不对称分布的,并且伴随有大幅值的风压脉冲,在反复的脉冲作用之下往往会导致局部破坏。Giofre et al[5]分析了矩形结构表面的风压时程概率统计特性,建议通过风压脉动的偏度值和峰度值对结构表面进行高斯区和非高斯区的划分。韩宁等[6]研究了方形高层建筑风压脉动的非高斯特性,结果表明风向角对非高斯区域有很大影响。楼文娟等[7]研究了切角超高层建筑的非高斯特性,给出了高斯与非高斯的判断区间,并提出在实际应用中对非高斯区的峰值因子取值偏小。Ko et al[8]对方形结构进行了风洞试验,结果表明结构侧风面存在非高斯特性,应适当提高围护结构的设计风荷载。曾加东[9]通过对矩形断面侧面风压系数概率密度的分析,并基于中国现行荷载规范,对现行规范中侧边极值风压取值分区形式进行细化。杜晓庆等[10-11]采用大涡模拟的方法,研究了标准方柱表面非高斯特性随风向角变化规律及切角措施对方柱风压非高斯特性的影响机理。
综上,已有文献对于方形断面脉动风压的非高斯特性研究较为全面,圆角化处理会明显改善标准方形断面的整体气动性能,但其局部区域的表面风压仍会出现非高斯特性,然而目前对于圆角方形断面脉动风压的非高斯特性以及风压极值研究较少。鉴于此,本文基于风洞试验,以标准方形断面和不同圆角率的方形断面为研究对象,分析模型表面脉动风压非高斯特性及峰值因子取值,计算其极值风压系数,得到风向角统计意义下的极值风压系数。
1 风洞试验概况
风洞试验在石家庄铁道大学STDU-1风洞实验室高速试验段进行,该试验段宽2.2 m,高2.0 m,试验段长5.0 m。本试验流场为低湍流度的均匀流场,湍流度约为0.5%。试验雷诺数Re=1.2×105,对应风速为14.58 m/s。
试验模型如图1所示,模型截面圆角半径为R,厚度D=120 mm,圆角率为R/D,试验测试了圆角率为0(标准方形断面)、0.1、0.2、0.3、0.4的圆角方形断面。由于模型为对称结构,因此试验风向角α的变化范围为0°~45°,变化步长为5°,试验风向角定义如图1所示。图2为试验模型布置示意图,模型长L为1 700 mm,为消除端板效应保证风场的二维流动性,在模型的两端设置直径De为600 mm的金属圆形端板。为保证模型具有足够的强度和刚度,在模型中央设置有实心钢棒。模型支撑于风洞中间位置,在试验风速下模型没产生变形,且未出现明显的振动。试验照片如图3所示。

图1 试验模型风向角示意图

图2 试验模型布置示意图

图3 试验照片
在模型的跨中位置处沿着周向布置有一圈测点,并在角点处做加密处理,不同圆角率模型的测点布置如图4所示。为方便论述,标记模型的4个角点分别为a点、b点、c点、d点,迎风面中点和背风面中点记为o点和p点。

图4 试验模型测点布置图
2 脉动风压的非高斯特性
风压非高斯特性产生的原因主要与结构周围流场中的旋涡运动有关,对于大面积的风荷载由于流场中空间相关衰减快,相关性很小,即空间内每个点涡作用都是独立同分布的,符合中心极限定理,一般服从高斯分布,否则服从非高斯分布[12]。高斯分布在其概率密度曲线上属于对称分布,其相应的风压时程样本也是均匀对称分布的,而非高斯分布相应的风压时程具有明显的不对称性,且伴随有大幅值的风压脉冲。
基于以上理论,图5和图6分别给出了圆角方形断面在0°风向角下迎风面中间测点(o点)和背风面中间测点(p点)的风压时程图及其概率密度分布曲线,由于圆角率为0.2、0.3、0.4时,其概率密度曲线图相似,因此只对圆角率为0.4的圆角方形断面进行展示。从图5和图6中可以看出,进行圆角化处理后,迎风面中间测点的风压时程分布较为均匀,圆角率为0.1时测点o的概率密度曲线呈现出较小的负偏现象,而圆角率为0.4时测点o的概率密度曲线与标准高斯过程接近。圆角率为0.1时,测点p的风压时程也出现了负向脉冲,其概率密度函数在左侧表现出拖尾现象。圆角率为0.4时,测点p的非高斯特性相较于圆角率为0.1时明显减弱,测点风压时程有脉冲作用,其概率密度函数在右侧表现出拖尾现象。

图5 圆角方形断面典型测点风压时程图
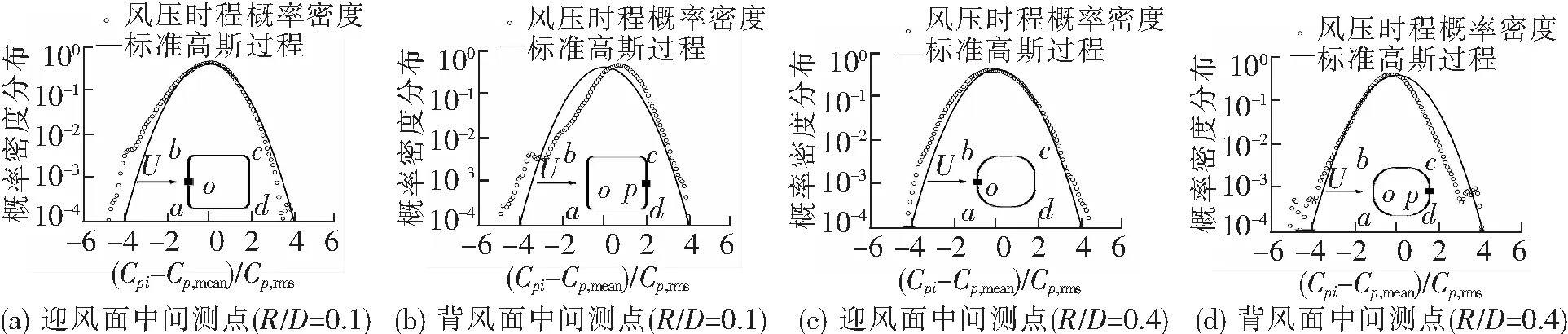
图6 圆角方形断面典型测点风压时程概率密度分布图
中国《建筑结构荷载规范》(GB 50009—2012)中根据Davenport所提出的传统峰值因子法,建议采用围护结构设计的峰值因子取2.5(保证率为99.38%)[13]。然而在运用相关计算理论(如极值穿越理论、可靠度理论)对峰值因子进行计算时,峰值因子是穿越率v、时间段T和保证率P的函数,即是与具体工况相关的,而中国规范取值为定值,且相较于实际工程中取值较低[14]。
计算峰值因子时,将峰值因子时程与风工程的典型曲线拟合,得到一定保证率下峰值因子取值[14]。峰值因子时程计算方法如下
原住民迁出后,很多住民在古建筑旁边选址新建房屋,这些现代混凝土建筑与明清时期古建筑群风格相差很大,与周边环境无法融合,新老建筑的杂陈,极大破坏了古村落街巷空间的连续性和整体景观之美,说明流坑村的保护前期缺少长期的整体规划,对于房屋的新建、改建缺乏管制。除此之外,街巷内电线杆、商铺广告牌、墙壁涂鸦、非机动车的停放等,以及新建的旅游设施,这些现代化元素逐渐侵蚀古村原生风貌[2]。
(1)
式中,Cpi(t)为测点风压时程;Cp,mean为平均风压系数;Cp,rms为脉动风压系数。
用高斯曲线拟合各测点的峰值因子概率密度曲线,并设定每个测点的峰值因子概率密度曲线的保证率为99.38%,通过此方法针对每个测点都得到一个峰值因子取值,表1中列出图5中典型测点的峰值因子取值。从表1可知,典型测点峰值因子取值均大于规范值。结合图6可知,当测点风压概率密度曲线表现出拖尾现象时,其峰值因子取值更大,且拖尾现象越强烈,峰值因子取值越大,由此可知其风压时程中出现的脉冲作用对峰值因子影响较大。

表1 典型测点峰值因子取值
3 极值风压系数
(2)
(3)
根据计算得到的每个测点的峰值因子,计算表面极值风压系数,并得到其随风向角的变化规律,由于圆角率为0.2和0.3时,其变化规律与圆角率为0.1或0.4时相似,限于篇幅以下只对圆角率为0.1和0.4的圆角方形断面进行展示,其中a、b、c、d分别为圆角方形断面的4个角点。
如图7展示了不同圆角率方形断面正向极值风压系数随风向角的变化,从图7可以看出,圆角率为0.1时,不同风向角下ab面的正向极值风压系数极大值均在1.05附近,且极大值点随着风向角的增大从ab面中点位置逐渐向b点移动。随着圆角率的增大,ab面正向极值风压系数随风向角变化规律与圆角率为0.1时相似,只是在a、b2个角点附近负压区明显增大。

图7 不同圆角率方形断面正向极值风压系数随风向角的变化
圆角率为0.1的圆角方形断面在bc面正向极值风压系数随风向角增大呈先减小后增大的趋势,随着测点位置由b点向c点移动,其变化的幅度逐渐减小。在0°和5°风向角时,bc面的正向极值风压系数不随测点位置的改变而改变,当风向角增大到10°左右时,b点处正向极值风压系数值突然减小,c点处正向极值风压系数值突然增大。当圆角率增大到0.4时,5°风向角时bc面所受负压突然增大,然后随着风向角的增大,负压逐渐减小并逐渐增大为正压。在bc面靠近c点的圆弧处随着测点位置向c点靠近,其正向极值风压系数逐渐增大。
cd面在0°和5°风向角时,所有模型的正向极值风压系数不随测点位置的改变而改变,随着风向角的增大,圆角率为0.1的模型在cd面中点附近形成较大的正压区,并且出现一个极大值,并在20°风向角附近极大值达到最大,随着圆角率的增大,此极大值逐渐减小。当圆角率为0.1时,d点附近正向极值风压系数随着风向角增大而逐渐增大,并在45°风向角时达到最大值,约为1.66,而随着圆角率的增大,d点附近正向极值风压系数逐渐减小。
图8展示了不同圆角率方形断面负向极值风压系数随风向角的变化。从图8可以看出,在ab面的a点处均受负压,测点负向极值风压系数绝对值随风向角增大而逐渐增大,其变化幅度明显大于正向极值风压系数,其余测点处变化规律与正向极值风压系数相似。

图8 不同圆角率方形断面负向极值风压系数随风向角的变化
圆角率为0.1时,负向极值风压系数绝对值在b点附近和c点附近均出现极大值点,且随着圆角率增大,靠近b点的极值点绝对值逐渐减小,而靠近c处的极值点绝对值逐渐增大,并逐渐远离c点。
在cd面,所有圆角方形断面在0°和5°风向角时负向极值风压系数绝对值随测点位置改变不大,且随圆角率增大而逐渐减小。在0°~5°风向角内绝对值随风向角增大而略有减小,在5°~45°风向角范围内,随着风向角增大,靠近d点处测点负向极值风压系数绝对值逐渐增大,其余测点随风向角增大呈先增大后略有减小的趋势。圆角率为0.1时负向极值风压系数绝对值最大值出现在45°风向角时d点附近,其值为-5.01,随着圆角率增大,其绝对值最大值逐渐向cd面中点附近移动,且绝对值逐渐减小。
圆角率为0.1的圆角方形断面在cd面中间区域会有较大的负压区,而da面中点处没有出现,da面其余测点负向极值风压系数大致与cd面呈对称分布。随着圆角率的增大,da面负向极值风压系数不再与cd面呈对称分布。
将圆角方形断面的正向与负向极值风压系数进行360°全风向角统计,得到统计意义下极值风压系数,如图9所示,由于模型为对称截面,因此只展示1/8面结果进行分析,其余侧面均与所展示ob段呈对称分布。对于统计意义下正向极值风压系数,标准方形断面和圆角率为0.4的圆角方形断面不同测点位置的正向极值风压系数大体相同,均略大于1。而圆角率为0.1、0.2、0.3的圆角方形断面,其正向极值风压系数波动较大,波动程度随着圆角率的增大而逐渐变小;随着圆角率的增大,各圆角方形断面正向极值风压系数最大值从角点(b点)处逐渐向中点(o点)处移动。统计意义下圆角率为0.1时正向极值风压系数最大值为1.66;圆角率为0.2时最大值为1.36;圆角率为0.3时最大值为1.24。整体上圆角率为0.1时正向极值风压系数最大。
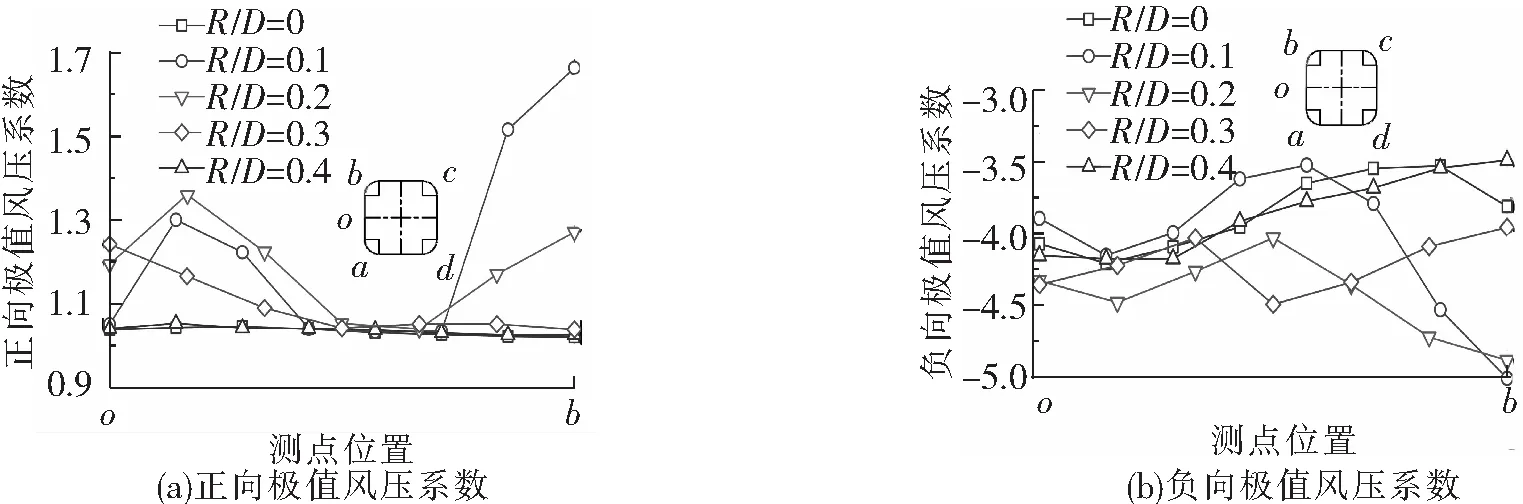
图9 风向角统计意义下极值风压系数
从图9(b)中可以看出,模型所受负向极值风压绝对值明显大于正向极值风压。对于统计意义下负向极值风压系数,标准方形断面和圆角率为0.4的圆角方形断面随测点位置的变化趋势相同,均是从中点(o点)向角点(b点)绝对值逐渐减小;圆角率为0.1和0.2时变化趋势相同,从中点(o点)向角点(b点)绝对值呈先增大后减小然后继续增大的趋势,均在角点(b点)处绝对值达到最大;圆角率为0.3时,负向极值绝对值在ob段中点达到最大。统计意义下圆角率为0时负向极值风压系数绝对值最大为4.21;圆角率为0.1时绝对值最大为5.01;圆角率为0.2时绝对值最大为4.89;圆角率为0.3时绝对值最大为4.49;圆角率为0.4时绝对值最大为4.18。整体上圆角率为0.1时负向极值风压系数绝对值最大。
4 主要结论
基于刚性模型测压风洞试验研究了雷诺数Re=1.2×105时标准方形断面和不同圆角率的圆角方形断面脉动风压的非高斯特性,讨论了峰值因子取值,并进一步分析了极值风压系数的分布规律,得到了如下几点结论:
(1)在均匀流场中,相较于标准方形断面,圆角方形断面脉动风压也具有明显的非高斯特性,并且在非高斯特性明显的区域峰值因子大于规范取值。
(2)风向角统计意义下,标准方形断面和圆角率为0.4的圆角方形断面正向极值风压系数在1附近,负向极值风压系数绝对值在各面中点附近更大,其值在-4.2左右。圆角率为0.1时,最大正向极值风压系数和负向极值风压系数绝对值均出现在角点处,其值分别为1.66和-5.01。圆角率为0.2和0.3时,最大极值风压系数介于圆角率为0.1和0.4的最大值之间。
