断簧对浮置板轨道结构振动特性的影响分析

2022-12-19王明生董奇奇

石家庄铁道大学学报(自然科学版) 2022年4期

王明生，董奇奇

(石家庄铁道大学土木工程学院，河北石家庄 050043)

地铁作为城市轨道交通主要方式之一，它有运量大、速度快、准点、安全的优点，因此，在各大城市飞速发展。然而地铁在给人们带来便捷的同时也给周围环境带来了振动与噪声污染，振动噪声打扰人们生活，地铁下穿的建筑物也会受到振动的影响[1-5]。Gladwell et al[6]研究表明地铁对周围结构和建筑物的影响主要表现为低频振动，在众多地铁减振方式中，钢弹簧浮置板道床低频减振效果较为显著[7-10]，因此越来越多的钢弹簧浮置板轨道应用于地铁减振。钢弹簧隔振器将浮置板道床与基础分离，起到支撑轨道系统的作用，每个钢弹簧都承受了来自道床的荷载作用[11]。钢弹簧受压强度大，随着时间的推移，钢弹簧在列车荷载反复作用下可能发生断裂，增大周围钢弹簧的受压强度，加速周围钢弹簧断裂，降低地铁列车平稳性和舒适性，严重时还会引起列车行车安全隐患[12]。因此对钢弹簧隔振器失效的研究是必要的。

关于钢弹簧隔振器失效对车轨系统的影响，国内外众多学者开展了很多相关研究。董北北[13]通过车辆轨道二维耦合模型，得出钢弹簧失效对轨道不平顺二次导有很大影响。吴磊[11]研究表明少数钢弹簧失效会增大道床垂向变形位移。多位学者通过建立车辆轨道耦合模型，研究了钢弹簧失效数量和失效位置对轨道系统的影响[14-18]。Zhao et al[19]通过有限元仿真研究分析得出，钢弹簧失效对车辆安全性和平稳性有显著影响。余关仁等[20]研究表明侧置隔振器失效的危害比内置隔振器的大。

以上对钢弹簧损伤的研究大多数集中在现浇式浮置板轨道，对于短板预制式浮置板的研究仍比较缺乏，有待完善。本文建立了车辆-预制式钢弹簧浮置板轨道耦合三维有限元模型，设立不同钢弹簧损伤工况，分析了钢弹簧损伤数量和损伤位置对车轨系统振动特性的影响。

1 车辆浮置板轨道有限元模型建立

图1为车辆-轨道耦合动力学模型，车辆选用地铁B型车，3节编组，取最高行驶速度80 km/h，单个车厢是由1个车体、2个转向架、4个轮对以及对应的一系悬挂和二系悬挂组成的。车体和构架考虑横移、浮沉、点头、摇头和侧滚方向的自由度，轮对考虑横移、浮沉、摇头和侧滚方向的自由度，轴箱考虑点头方向的自由度，单个车厢共计39个自由度。主要参数如表1所示。利用ABAQUS建立柔性钢轨和浮置板道床，采用中国CHN60钢轨，选用solid45实体单元对钢轨和浮置板道床进行建模，将建好的模型导入到SIMPACK多体动力学软件，用弹簧元件模拟扣件和钢弹簧，在SIMPACK里建立车辆模型，设置轮轨关系，有限元模型如图2所示。为了排除其他因素的干扰，计算中不考虑轨道不平顺的影响。

表1 车辆、浮置板主要参数

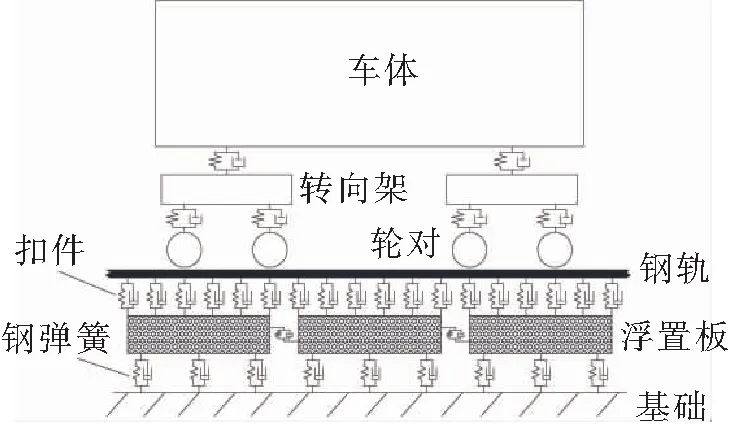
图1 车辆-轨道动力学模型

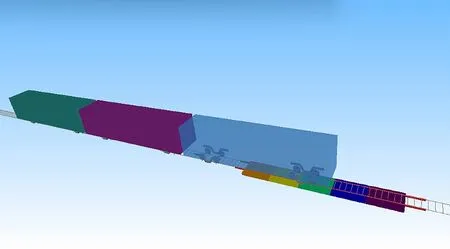
图2 车辆轨道有限元模型

2 动力学仿真分析

2.1 工况设置

钢弹簧隔振器损伤形式较多，如刚度折减、刚度部分失效等，本文仅考虑钢弹簧隔振器完全失效的情况。地铁运营过程中，钢弹簧隔振器数量较多以及浮置板自身刚度大，个别钢弹簧失效较难发现，很可能出现不同位置、不同数量的钢弹簧失效，因此将探讨不同位置和不同数量钢弹簧失效对浮置板轨道系统动力特性的影响。为了提高计算效率并且减少边界对计算结果的影响，模型建立了5块3.6 m长的浮置板道床，仅考虑第3块浮置板道床下的隔振器失效。为方便研究对一侧钢弹簧所在位置标记为A、B、C，如图3所示。图4(a)～图4(h)为各个工况，图4中标黑的点表示所在位置的钢弹簧失效。

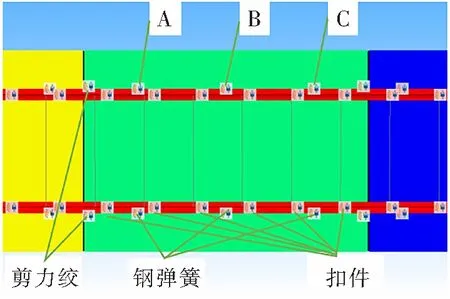
图3 钢弹簧浮置板轨道

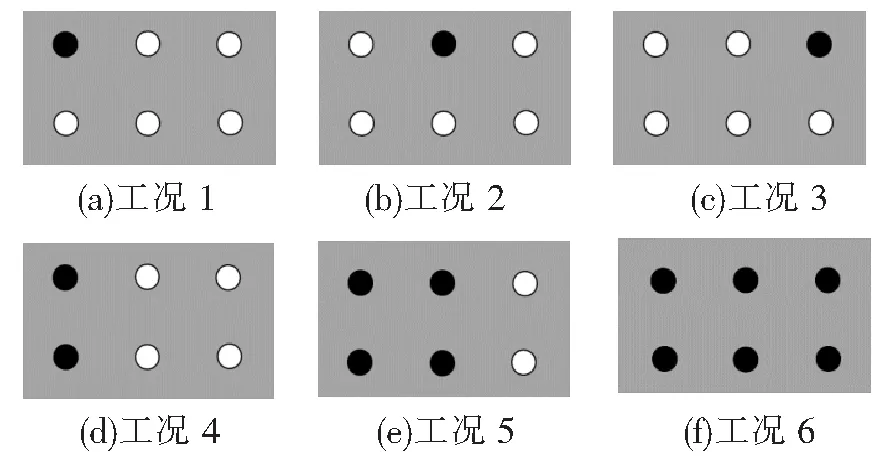
图4 钢弹簧失效工况

2.2 不同数量的钢弹簧失效对浮置板轨道动力特性的影响

图5(a)、图5(b)和图5(c)分别为车体、钢轨和浮置板垂向加速度时程曲线，从图5(a)可以看出，不同数量的钢弹簧失效时，各工况车体垂向加速度趋势上变化明显，但数值差异较小，最大值为工况6的0.11 m/s2,均小于《铁路线路修理规则》(铁运[2006]146号)中所规定的二级舒适度标准允许偏差值0.15g。从图5(b)和图5(c)可以看出，钢轨垂向加速度随着钢弹簧失效数量的增加变化不明显，且远小于规范限值2 000 m/s2。浮置板垂向加速度随钢弹簧失效数量的增加而微微增大，最大值为工况6的6.48 m/s2，均小于规范限值200 m/s2。由此可以看出不同数量的钢弹簧失效对车体、钢轨和浮置板的垂向加速度影响较小。

图5(d)和图5(e)分别为浮置板和钢轨垂向位移时程曲线，图5(f)为钢轨垂向位移幅值沿线路纵向分布情况。由图5(d)可知,浮置板垂向位移随钢弹簧失效数量的增加而增大。在无钢弹簧失效时，浮置板最大位移为1.82 mm，钢弹簧失效数量为1、2、4、6个时，浮置板最大垂向位移分别为2.08、2.39、2.93、3.62 mm，相较于无钢弹簧失效时分别增大了14.3%、31.3%、61.0%、98.9%，其中工况6的钢弹簧垂向位移幅值超过了规范限值3 mm。由图5(e)和图5(f)可知，钢轨垂向位移随钢弹簧失效数量的增加而增大，无钢弹簧失效时，处于浮置板端部的钢轨垂向位移幅值比中部的大。无钢弹簧失效时钢轨最大垂向位移为2.71 mm，工况1、4、5、6情况下的钢轨垂向位移最大幅值分别为3.07、3.31、3.99、4.69 mm，相对于钢弹簧完好状态下分别增大了13.3%、22.1%、47.2%、73.1%，其中工况6的钢轨最大垂向位移超过了规范限值4 mm。断簧位置的浮置板失去支撑，该部位以及对应的钢轨在列车经过时向下位移的距离增大，由于浮置板较好的整体性，在列车经过之后会恢复原位。

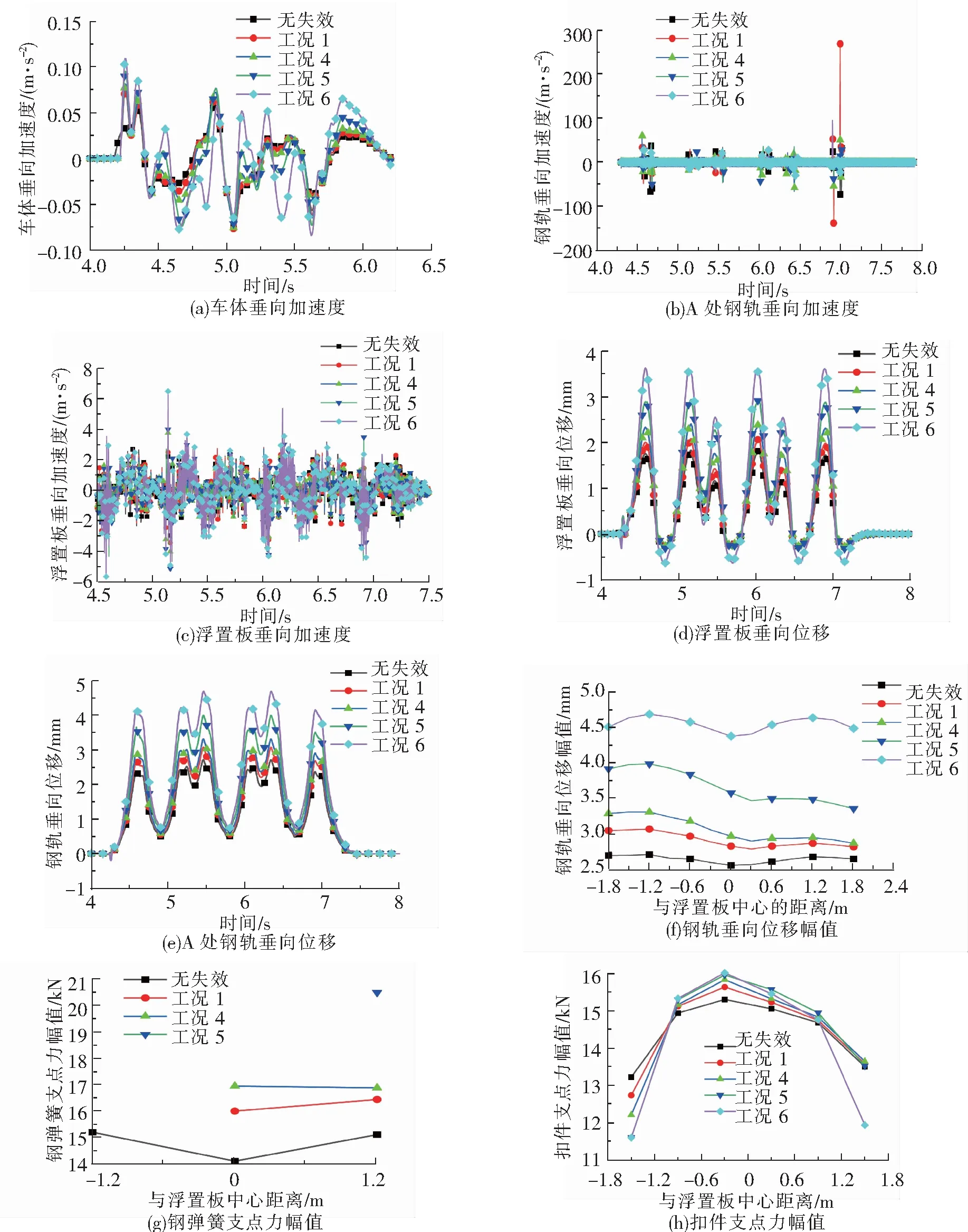
图5 不同数量的钢弹簧失效对浮置板轨道动力特性的影响

图5(g)和图5(h)分别为钢弹簧和扣件支点力幅值沿线路纵向分布情况。由图5(g)可知，无钢弹簧失效时，位于端部的钢弹簧支点力略大于中部的钢弹簧支点力，当有钢弹簧失效时，断簧位置的钢弹簧支点力骤减为0，该部分的荷载由周围钢弹簧承担，周围钢弹簧支点力增大，失效数量越多，周围钢弹簧支点力越大。由图5(h)可以看出，处于浮置板端部的扣件支点力随着钢弹簧失效数量的增加而减小，而处于中部的扣件支点力则随着钢弹簧失效数量的增加而增大，且增加趋势随钢弹簧失效数量的增加而减小。

2.3 不同位置的钢弹簧失效对浮置板轨道动力特性的影响

图6(a)和图6(b)分别为车体和浮置板垂向加速度时程曲线，从图6(a)和图6(b)可以看出,单个钢弹簧失效情况下，无论失效位置在板中还是板端，车体垂向加速度和浮置板垂向加速度差异都较小且变化趋势接近，均满足规范。

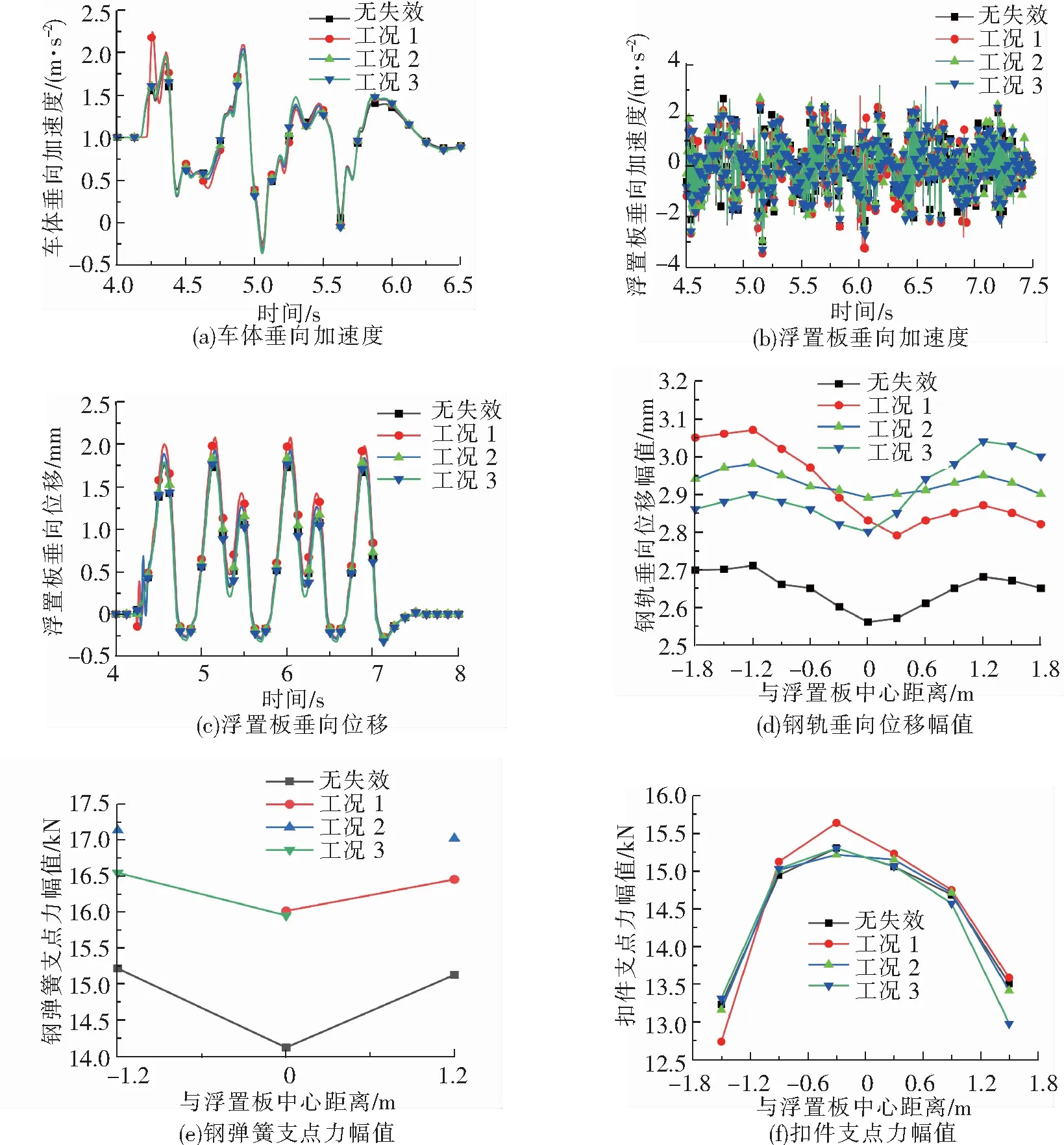
图6 单个钢弹簧在不同位置失效对浮置板轨道动力特性的影响

图6(c)和图6(d)分别为浮置板垂向位移时程曲线与钢轨垂向位移幅值沿线路纵向分布情况图。从图6(c)可以看出，工况1、2、3情况下的浮置板垂向位移幅值为2.08、1.93、1.85 mm，与无钢弹簧失效情况下的1.82 mm相比，分别增大了14.3%、6.4%、1.6%。从图3和图6(d)可知，随着同一块浮置板下单个钢弹簧失效的位置沿线路纵向距离的增加，浮置板垂向位移则减小。无钢弹簧失效和单个钢弹簧失效情况下，位于板端的钢轨垂向位移幅值均大于中部，且任意位置的单个钢弹簧失效均会导致各点钢轨垂向位移幅值的增大。与钢弹簧完好状态下相比，工况1的钢轨垂向位移最大增幅位于A处，为0.36 mm；工况2的钢轨垂向位移最大增幅在B处，为0.33 mm；工况3的钢轨垂向位移最大增幅位于C处，为0.36 mm，即钢弹簧失效位置处的钢轨垂向位移增幅最大，且板端影响比板中的大。

图6(e)和图6(f)分别为各点钢弹簧、扣件支点力幅值沿线路纵向分布情况图。由图6(e)可知，板端的钢弹簧支点力大于板中，单个钢弹簧失效情况下，它周围的钢弹簧支点力均增大，工况1、2、3分别增大1.9、1.92、1.83 kN。板中钢弹簧失效时周围钢弹簧支点力要大于板端钢弹簧失效时周围的钢弹簧支点力，这是由于板端钢弹簧失效时，相邻浮置板通过剪力铰分担了支点力。由图6(f)可以看出，板端钢弹簧失效会引起相近位置的扣件支点力减小，相远位置支点力微微增大，而板中钢弹簧失效对扣件支点力的影响较小。