基于波束形成的三维传声器阵列仿真

崔丽兰， 田杨萌， 王彩霞， 刘琳， 张潇艺

(北京信息科技大学理学院， 北京 100192)

随着近年来科学技术的不断发展，声源定位技术[1]在军事领域、自然探索领域、工业领域和民用领域等都有非常重要的作用。基于传声器阵列的声源定位技术成为研究热点之一。

传声器阵列声源定位技术是使用传声器阵列采集提取声信号，然后对采集提取的声信号进行声信号的处理，进一步通过声源定位算法实现声源信号的定位[2]。传声器阵列是指多个传声器按照一定的几何结构进行排布组成的阵列，具有很强的空间选择性，无须移动就可以对声源信号进行检测、定位与跟踪，因而在语音增强、声源定位、回声消除等方面有着极大的应用空间。传声器阵列声源定位技术的定位结果与其传声器的阵列阵型排布有着密不可分的关系[3]。针对于所适用的环境与应用目的，不同的传声器阵列有着特定的优势，对一维、二维和三维阵列进行不断探索与优化，比如对一维直线型麦克风阵列的优化来提高定位效率[4]；使用二维、三维阵列探测汽车非法鸣笛[5]；使用正四面体阵列进行机器人声定位性能改进[6]等。 Padois等[7]比较了将各种麦克风阵列配置为二维和三维对声源定位的影响，研究发现，当添加垂直方向上的麦克风阵列可有助于提高平面阵列的空间分辨率。柴国钟等[8]通过仿真与实际声场实验，基于三维声聚焦波束形成方法对伞型三维传声器阵列与轮辐平面传声器阵列进行了识别单声源的对比，验证了伞型阵列可以识别阵列前后面，但伞型在X方向的主瓣宽度较小，Y方向的主瓣宽度控制的较差，此由于两个方向阵列排布的对称性不同，不对称性对缩小主瓣宽度具有明显优势。Ping等[9]利用稀疏贝叶斯学习方法，提出了一种使用球面波传播的刚性球形麦克风阵列的三维声源定位模型，在三维空间中进行定位，此种方法得到了精确的定位数据，并且实现了在三维空间中定位多声源的问题。他们都对传声器阵列结构进行了研究，对三维阵列研究具有重要意义，但是没有进行对比分析。

通过基于最小方差无失真(minimum variance distortionless response, MVDR)波束形成算法的传声器阵列声源定位原理，设计相同阵元数不同阵列类型的三维阵型进行声源定位，达到提高在空间域360°内户外多干涉噪声源环境下的声源定位精度的目的。在满足传声器阵列的设计要求下，保持阵元数目相同，设计为三棱锥、正四面体三维阵列及对球型阵列进行改进优化的旋排球型阵列等三维阵列，通过MVDR波束形成算法对不同阵列进行声源定位，对结果进行分析比较确定较优的声源定位三维阵列模型，即最优的传声器阵列结构在一定程度上可以提高波束形成指向中的主瓣，降低或抑制旁瓣、防止栅瓣的干扰，具有较高方位角和俯仰角的定位精度。通过仿真实验进行对比，证明此方法的有效性，对三维传声器阵列的使用与优化提供一种改进方案。对传声器阵列的优化与探索是为了进一步提高对空间信息的利用率，提高定位精度，抑制噪声源的干扰，对三维麦克风阵列的研究与优化具有十分重要的研究意义和应用前景。

1 传声器阵列声源定位技术

传声器阵列声源定位技术是模拟人的耳朵对声音的定位原理，其传声器阵列是通过利用几个甚至上千个传声器，按照一定的规则进行排列来构成各种阵型。多个传声器同时工作采集声信号，利用声源定位算法，求得声源信号的位置。

基于传声器阵列声源定位技术进行声源信号的定位原理：首先，选取实现目的最优的传声器型号，设计合适的传声器阵列，进行声信号的采集；然后对声信号作预处理，放大并滤除干扰噪声；再对声信号进行基于MVDR波束形成算法处理；最后得到声源信号的位置。如图1所示。

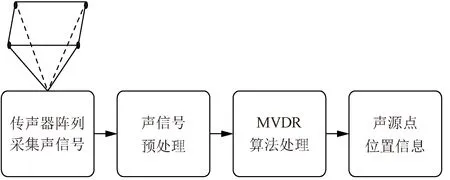
图1 传声器阵列声源定位流程图Fig.1 Microphone array sound source localization flow chart

2 波束形成算法

目前，应用于传声器阵列的声源定位的算法主要分为基于到达时间差(time different of arrival, TDOA)算法、基于波束形成(beamforming, BF)算法以及声全息(holography)算法[10]。在中远距离的定位算法中，波束形成算法能够对阵元采集的声信号做适当的加权，对阵列接收的有用信号及其特征信息进行提取，同时对噪声干扰或无用的信号进行抑制，提高声源定位精度。此种信号处理技术不仅可以灵活控制波束，具有提高信号增益、抗干扰能力强的特点，还有空间分辨率能力高的特点，可用于稳态和非稳态声源以及缓慢运动声源的识别，在成本、效率和实时性等各个方面具有优势的声源识别算法[11]。

波束形成方法的分类可根据采用不同的方法获取加权矢量分为三种类型[12]：第一种波束形成方法是指与参考信号数据无关，比如常规波束形成；第二种波束形成方法是指使用最佳权矢量，此方法对阵列接收数据统计特性的估计有依赖，比如最大信噪比准；第三种波束形成方法是指自适应地根据接收数据变化来改变权矢量，比如最小方差无失真响应(MVDR)波束形成算法、递归最小二乘(recursive least squares, RLS)算法、最小均方误差(least mean square, LMS)算法等。

最小方差无失真响应(MVDR)算法的原理是在期望信号无失真的约束条件下，选择适当的滤波器系数，进一步最小化阵列输出的平均功率[13]。此算法使用自适应方式更新噪声协方差矩阵，使用相位加权广义互相关方法进行矢量估计，是应用最为广泛的自适应波束形成方法之一；且MVDR算法能处理干扰噪声源个数大于传声器个数的噪声，适合户外存在多干扰噪声源的处理。递归最小二乘法(RLS)算法原理是任意时间对全部输入信号估计的平方误差之和最小，其收敛速度明显加快，但是其计算复杂度较高，不利于实时性。最小均方误差(LMS)算法的原理是为找寻最优权值而沿着权值的梯度负方向进行搜索，来实现均方误差最小的自适应滤波，具有计算量小、实时性好等优势，但是该算法需已知期望信号，且用瞬态值代替稳态值，会造成失调的现象。故而，考虑阵列的适用环境更广，有效性更高，选取最小方差无失真响应(MVDR)波束形成算法进行研究。

设存在一个声源信号d(t)，对应波达方向为θd，J个干扰信号zj(t)(j=1,2,…,J)，对应波达方向为θzj，传声器阵列中每个阵元上的白噪声为nm(t),则m个阵元接收到的信号为

(1)

用矩阵表示整个传声器阵列为

(2)

式(2)中:a(θd)=[a1(θd),a2(θd),…,am(θd)]，表示波达方向θk(k=d,z1,z2,…)的声源方向。

通过加权向量w对传声器阵列接收到的数据加权就可以得到波束形成输出。快拍数为N的波束形成输出为y(t)，且y(t)=wH(θ)x(t)的平均功率为

(3)

当N→∞时，式(3)可表示为

P(w)=E[|y(t)|2]

=wHE[x(t)xH(t)]w

=wHRw=E[|d(t)|2]|wHa(θd)|2+

(4)

式(4)中:R=E[x(t)xH(t)]为阵列输出的协方差矩阵。

对式(4)计算得到的权重设置合适的约束条件，便可实现采集来波方向为θd的信号，同时虑除干扰信号，故而，权重的约束条件表示为

(5)

当传声器阵列的功率输出满足权重的约束条件，又要使噪声最小化，需要对输出函数进行优化处理，可表示为

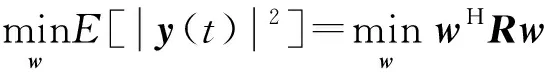
(6)

故可以将波束形成问题表示为

(7)

最小方差无失真响应(MVDR)算法用于信号信号处理时，即是对传声器阵列的每个阵元的权值进行求解计算。对式(7)中采用拉格朗日乘子法可得

L(w)=wHRw+λ[wHa(θd)-1]

(8)

其中λ为拉格朗日乘子。

对式(8)求导数，令其等于0，即

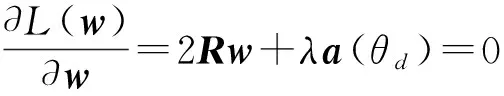
(9)

求解式(9)可得

w=μR-1a(θd)

(10)

式(10)中:μ为比例常数。

根据式(5)中的权重约束条件wHa(θd)=1与式(10)联立可得

(11)

由MVDR算法准则计算得到的最优权重可以表示为

(12)

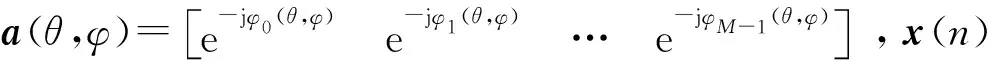
(13)

设θd为待求的角度值(θ,φ)的统一表示形式，定义空间滤波F是输出信号与输入信号幅度的比值，表达式为

(14)

f(θd)为归一化后的方向图，归一化后结果为

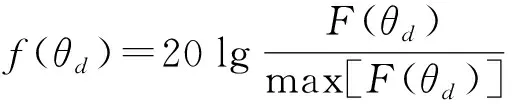
(15)

当f(θd)取得极大值时，所对应角度最接近入射波的入射角度。最小方差无失真响应(MVDR)算法在实现形式上简便，可以有效抑制旁瓣的干扰，可以对环境中存在多个噪声且噪声源的数目大于传声器个数的声信号进行处理，且其自适应的权向量与实际的数据相关联，来实现权向量及时更新，故此算法能够适应非平稳的环境，应对户外多噪声源的场景。MVDR算法可用于多种结构类型的阵列，具有广泛的适用性。

3 传声器阵列阵结构对波束指向性的影响

越来越多的应用场景的需求，不断促进着基于传声器阵列的声源定位技术发展。要使传声器阵列声源定位技术在不同的实际需求中充分发挥其优势，得到较高的定位精度，就要充分考虑使用此方法的条件。自适应阵列的结构决定了自适应波束性能的特点。当传声器阵元的位置发生变换时，自适应阵列的性能也随之发生很大的变化。传声器阵列设计的主要参数包括：传声器的空间排列，传声器阵元的个数，传声器阵元间的间距，传声器阵列的孔径；还包括波束指向性，波束宽度，最大旁瓣级等特征参数[14]。在理论基础上，需使用最少的传声器个数，并考虑实际情况来设计一个具有最好的声信号识别效果的实用型阵列。因此研究阵列结构、分析阵元位置对自适应波束的形成有着重要的意义。

3.1 一维、二维、三维阵列的阵型分析

不同数目的传声器按照一定的空间布局排列而成的称为传声器阵列。当传声器阵列拓扑结构不同时，例如阵列的维度、阵元的个数、阵元间距都会影响传声器阵列定位算法的定位精度与运算速度。传声器阵列的拓扑结构分为三类：一维阵列，如线型阵列；二维阵列，如十字型平面阵列；三维阵列，如正四面体三维阵列[15]。常见的三类传声器阵列的种拓扑结构如图2所示。在实际的空间定位过程中，一维阵列定位仅可对半个平面内搜索；二维阵列定位既可以在整个平面内搜索，也可以在平面为界的半个空间内搜索；三维阵列定位可以在整个空间内进行声源搜索。

图2 传声器阵列拓扑结构Fig.2 Microphone array topology

对于传声器阵列的声源定位研究，在实际测试中，由于传声器的制造本身存在公差，而且还有各种环境因素对其影响，导致传声器阵列接收信号的频率响应特性理论值与实际的测量结果存在较大偏差，将会影响定位结果，故校准与提升传声器阵列频率响应具有重要的意义。

3.2 阵元间距与声源定位的关系

传声器阵列设计需要考虑传声器之间的间距，输入信号空间分辨率，以及使用场景。对目标声源进行定位时，阵列孔径往往会影响系统的成本：阵列的体积、采样率的选择及定位效果等诸多方面。

一般情况下，阵元的间距和声源频率以及阵列系统的采样率有着很密切的联系[16]。以两个传声器为例，当声音信号波达角为θ时，两个间距为d的传声器之间相位差可以表示为

(16)

为了避免产生相位模糊，相位差需要满足φ≤π, 由此可得阵元间距需满足关系

(17)

所以由式(17)可知，阵元间距应小于等于声源信号波长λ的一半。当阵元间距大于声源波长的一半时，会在其他方向出现波束响应与波束主瓣相同的幅度值，即称为在其他方向上出现了栅瓣；因同等强度的信号从栅瓣方向入射产生的波束输出功率完全相等时，会干扰根据波束输出区分信号入射方向，故在设计阵列时，需要避免产生栅瓣。

而当单元数目一定时，间距越小阵列口径越小，导致阵列主瓣展宽。相反，当单元间距越大，阵列口径越大，导致阵列主瓣变窄。故单元间距的选择是根据主瓣宽度决定的，当然单元间距太小导致单元之间的强互耦也得注意。

3.3 阵元布局与声源定位的关系

对传声器阵列进行布局时，在考虑阵列间距满足合适范围内，根据间距可对阵型分为规则阵列和不规则阵列。规则阵列是指传声器之间的间距相同，即均匀划分子阵列[16]，此划分使得子阵级等效阵元的相位具有一致性，使得在周期内，有规律的形成与主瓣峰值相同，角度不同的波峰，即为方向图中出现的栅瓣，因为栅瓣与主瓣具有相同的水平，会对定位声源结果产生强烈的干扰。在对空间进行不断重复的采样会产生混叠问题，从而在波束图的仿真结果中会出现虚像。比如，常见的规则二维阵列有十字阵、矩形阵、圆形阵列、环形阵列等。不规则的阵列的是指随机摆放传声器的方位，对于非均匀的阵列可避免重复规律性的采样，即阻止栅瓣的形成，可避免出现混淆的影响。其中非均匀划分子阵的结构不同时，波束形成效果也不相同。比如，常见的二维不规则阵列有随机阵列、阿基米德螺旋阵列、车轮阵等。

3.4 阵列孔径与声源定位的关系

阵列孔径，是指传声器阵列采集声音信号的有效区域[17]。当传声器阵列的阵列孔径越大，相应的阵列结构就会越难实现。一个阵列的实现复杂程度往往是由传声器的数目和阵列孔径来决定。由数目较多的传声器组成的阵列，相对应的布线方法就会越繁杂。同时，传声器阵元的个数对阵列增益还有影响，即阵列的传声器个数越多，阵列增益越高。可通过改变阵元数目的多少来改变阵列的孔径。如图3所示，以均匀线传声器阵列为例进行仿真，保持阵元间距不变的情况下，即d=λ/2，设置阵元个数(N)由少变多进行改变，即N=8、N=16、N=24。

由图3可知，当逐渐增加传声器阵元个数，波束方向的主瓣逐渐变窄，即阵列的指向性随着阵元的数目增多而越来越高。另外，为了提高传声器阵列的分辨率，则要求孔径(D)要大；但是阵列要有较高的截止频率，要求较小的阵列间距。孔径间距大小是相互矛盾的，在实际使用中往往针对具体的被测对象来权衡设计。比如，圆阵收集到的信息较多，在不太容易丢失有效信号的同时会降低信噪比。线阵指向性很好，采用线扫方法，可以增加覆盖范围，但同时增加了计算量。

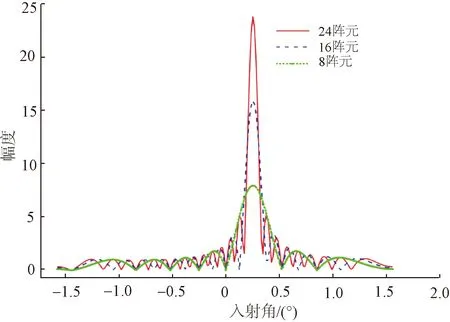
图3 不同阵元数目的均匀线阵方向图Fig.3 Pattern of uniform linear array with different number of elements

3.5 阵列的误差来源分析

在实际使用过程中，常见的阵列误差形式主要有三种，分别是阵元幅相误差、阵元互耦、阵元位置误差[18]。阵元幅相误差是由各个阵元和通道的幅度和相位特性不一致所导致；阵元互耦是各个阵元之间可能会相互影响而产生耦合效应(或称互耦效应)；阵元位置误差是每个阵元的真实位置在其标定的位置处出现了一定的偏差所导致的情况。本文主要针对阵元位置误差展开讨论。

假设入射声信号的方位角为φ，俯仰角为θ，如图4所示则为阵列接收信号的示意图，则可得其方向为x=-[cosθcosφ,cosθsinφ,sinθ]，阵元i的坐标设为Mi=(xi,yi,zi)，设每个阵元的真实位置在其标定的位置Mi处出现了Δd的偏差，此刻n个阵元的位置表达式为

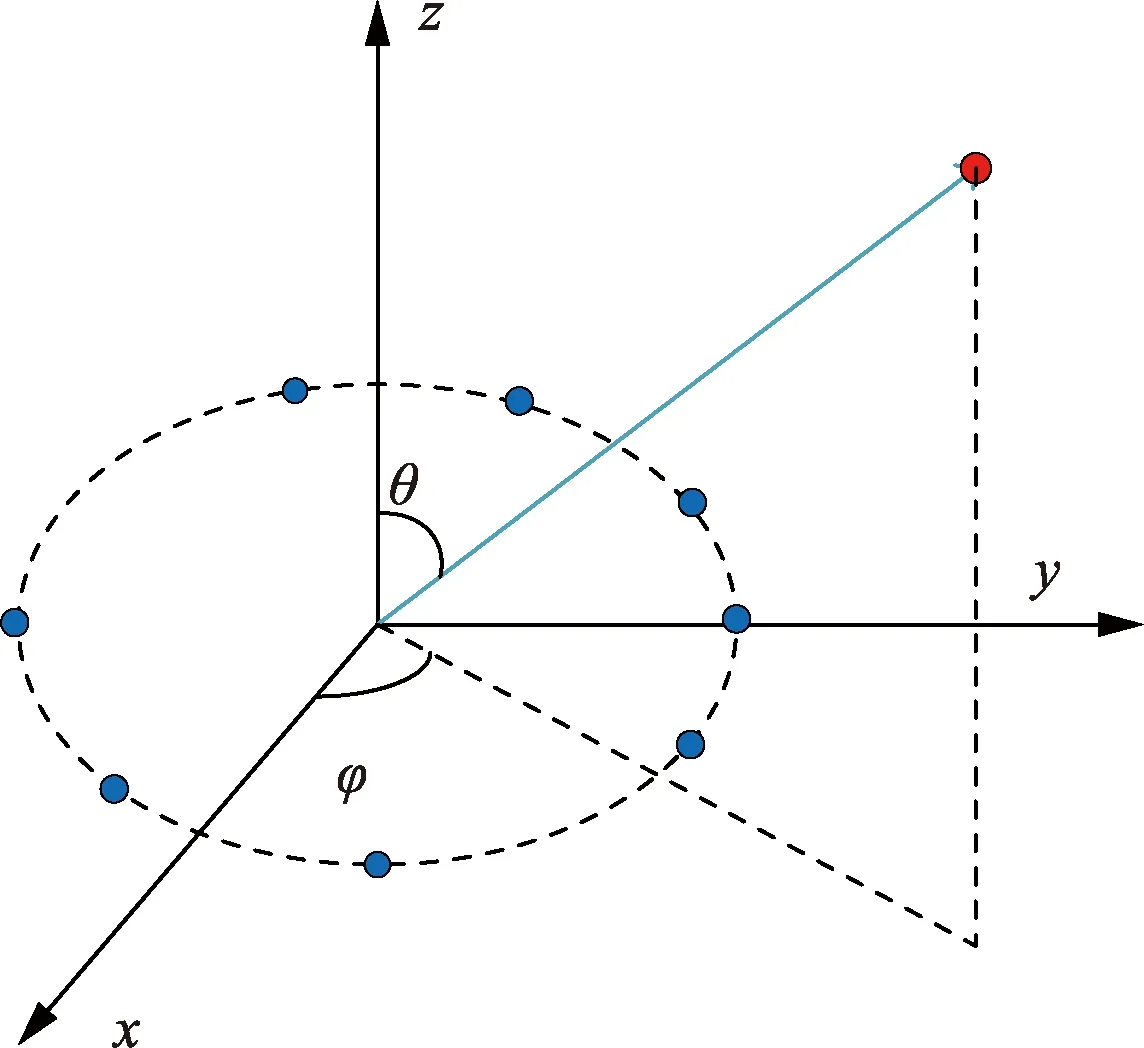
图4 阵列接收信号Fig.4 Array received signal

(18)

则存在位置误差的信号输入向量x′(n) 可以表示为

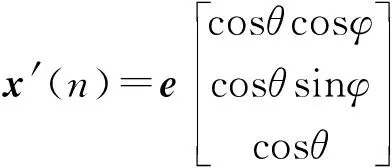
(19)

将式(19)代入空间相关矩阵中可得

R′=E{x′(n)x′H(n)}

(20)

将式(20)代入式(13)～式(15)中，即可利用MVDR波束形成算法计算出当存在阵元位置误差干扰情况的声源位置。

4 实验仿真与分析

本次实验设计是对200～800 Hz频段的声源点利用基于MVDR波束形成定位算法对声源进行实验仿真。当在理想情况下，设c为声速，为340 m/s,声源频率f为200 Hz≤f≤800 Hz，则根据式(17)可得对应的阵元距离范围可以计算得

d≤0.85 m,f=200Hz

(21)

d≤0.212 5 m,f=800Hz

(22)

所以在实际工作时，阵列阵元的间距要在这个范围内取值。

因为在户外情况下进行使用，阵列尺寸应该在满足阵列间距的条件下考虑到其便携性，不应该太大，将阵元间距控制在0.212 5～0.85 m；对于阵列中阵元的个数，多数情况下应该由系统需求来定，但是考虑声源信号处理应该尽量简单以及测量成本应该尽量低廉，阵元个数在5～20个之间最合适，本实验模拟采用16阵元的数目进行了实验仿真。

4.1 相同阵元不同阵型的仿真结果

为了研究相同阵元数目不同阵型的声源定位结果，设计同为16阵元数目的不同三维阵型的传声器阵列，分别为16阵元的三棱锥阵列、正四面体三维阵列、圆台、长方体、正方体、三维伞阵列、三维螺旋阵列、旋排球阵列(此阵型是将旋风形与球型两阵列的分布特点相结合，进一步优化得到的新阵列模型)。

实验仿真中的设置声源方位角为302°，俯仰角为55°，传声器的采样频率位2 kHz,使用MATLAB进行仿真，并生成图5～图12所示仿真结果。

图5 三棱锥阵列声源定位仿真图Fig.5 Simulation diagram of sound source location of tripyramid array

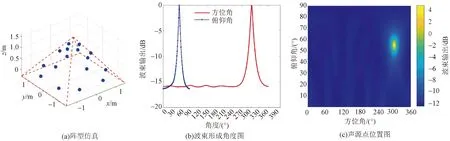
图6 正四面体三维阵列声源定位仿真图Fig.6 Simulation diagram of tetrahedral 3D array sound source location

图7 圆台阵列声源定位仿真图Fig.7 Simulation diagram of sound source location of circular array

图8 长方体阵列声源定位仿真图Fig.8 Simulation diagram of sound source location of cuboid array

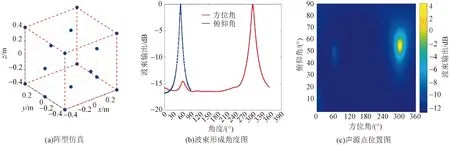
图9 正方体阵列声源定位仿真图Fig.9 Simulation diagram of sound source location of cube array

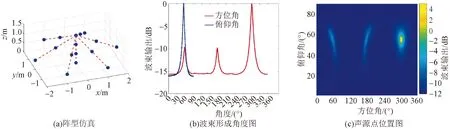
图10 三维伞阵列声源定位仿真图Fig.10 Simulation diagram of sound source location of 3D umbrella array

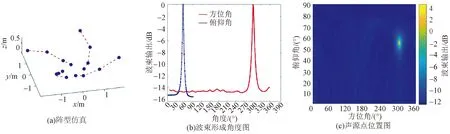
图11 三维旋风阵列声源定位仿真图Fig.11 Simulation diagram of sound source location of 3D cyclone array

图12 旋排球阵列声源定位仿真图Fig.12 Simulation diagram of sound source location of spinning volley array

4.2 仿真结果分析

根据上述仿真结果显示，当传声器阵列的阵元数目均为16阵元时，将传声器阵型设计为不同阵型时，各自阵型仿真定位的结果显示不同。本实验设计不同阵型的传声器阵列，对各种阵型使用基于MVDR波束形成定位算法进行实验仿真，定位声源位置的俯仰角定位亮点范围在2°～6°，方位角定位亮点范围在2°～8°，如表1所示。

表1 各种阵型的声源定位结果Table 1 Simulation diagram of sound source location of various formation

由表1的结果可以看出，当阵元数目相同时，三棱锥阵列阵型、三维旋风阵列阵型、旋排球阵型的声源定位范围误差较小，声源定位结果较好。由仿真实验结果可看出，对于三棱锥阵列、长方体阵列、正方体阵列以及三维伞型阵列的声源点位置图，在不同方位区域出现了较模糊的声源点，对真实的声源位置有一定程度的干扰。对于球型阵列的仿真结果，其定位声源点范围较小，且没有出现干扰声源点，是较为理想的定位阵型，且其俯仰角亮点范围仅为2°，方位角亮点范围为2°。

波束形成的性能与阵列的空间几何排布有关，故在考虑设置传声器阵列时，应该要充分考虑到阵元个数、阵列孔径的大小及阵元间距对阵列声源定位的影响。当阵元间距的距离设置不合适就会导致出现栅瓣。根据图3仿真结果可看出，当增加传声器阵列的阵元个数，其波束的主瓣宽度逐渐变窄，阵列指向性得到了提升。如图5～图12中使用16阵元的不同三维传声器阵列仿真结果中，最初构建阵列阵型时，考虑到阵元个数、阵列孔径的大小及阵元间距，设置在符合要求的范围内，避免了栅瓣的出现；再经过MVDR波束形成算法的处理，在一定程度上降低了旁瓣的干扰，得到具有较高分辨率的波束指向结果。其中，旋排球型与三维的旋风型的方位角与俯仰角指向性优于其他阵列。

针对户外的多噪声源环境，采用MVDR算法可以处理当噪声源数多于麦克风阵元数目的定位，在一定程度上可提高户外麦克风阵列的便携性，且在经济上实现较低成本。球型的传声器阵列具有高空间分辨率，具有对于空间内各个方向的波束形成等优点。考虑到阵列的均匀布局与非均匀布局对信号采集的优缺点问题，本实验在设计球型时采取优化布局形式，对16阵元的传声器较均匀分布于球型的表面，并且设计时考虑类似旋风型阵列的定位的非均匀分布，进行旋风阵列与球型双阵列结合形式，提出球型的优化模型——旋排球型阵列进行仿真，进一步避免均匀布局对信号采取时出现空间信号的重复采集出现的栅瓣现象。可以从仿真结果中看出，优化后的球型阵定位结果的主瓣宽度更窄，说明优化后的球型阵列具有更高的指向性。

5 结论

基于传声器阵列的声源定位技术在较短时间内精确的定位到声源点的位置具有很重要的应用价值，对传声器阵列不断的优化，选取最适合、最能准确定位的阵型是需要解决的问题。对三维的传声器阵列阵型进行了初步探索，并利用基于MVDR波束形成算法通过使用MATLAB进行了实验仿真，在固定频段200～800 Hz频段的声音探测时，相同阵元数目的不同三维传声器阵列中，得出旋排球型阵列测得的声源定位点的波束指向性更高，定位精度最好，对于实际应用具有一定的参考。本实验是在理想情况下进行的实验仿真，下一步将考虑在实际情况下测量时，深入研究外界环境噪声因素对此方式的影响。