浅埋隧洞下穿既有建筑物爆破施工振动分析*

黄俊树，秦天戈，陈水和，吴明泽，李丽平，吴 立

(1.浙江省隧道工程集团有限公司，杭州 310030；2.中国地质大学(武汉)，武汉 430074)

随着我国水利水电以及其他地下工程建设的迅猛发展，下穿地表的工程在进行爆破掘进时引起的振动会对既有建筑物产生很大的负面影响，因此爆破方案安全性成为了爆破作业中应该重视的关键一环，需要我们进行更加深入的探讨。

由于爆破作业具有极大的破坏性，因此需要对爆破方案进行安全性评价，在实施控制爆破之前进行数值模拟计算成为一种趋势，许红涛、杨建华、卢文波等在圣维南原理基础上分析了数值模拟方法在不同加载方式条件下的优势[1,2]，研究结果为数值模拟加载方式提供了不同的选择；吴昊利用有限差分软件模拟了复杂地层浅埋暗挖隧洞下穿地下商业街的过程[3]，验证了工程利用超长大管棚的支护办法、深孔注浆地层加固和减振爆破等技术的有效性；另外，刘彦涛利用ANSYS/LS-DYNA，在爆轰理论及爆轰压力算法的基础上采用等效荷载的加载方式模拟了隧洞下穿寺庙的爆破振动效应[4]，为控制爆破方案提供了参考意见；康永全等利用ANSYS/LS-DYNA，通过共节点加载的方法[5]，在炮眼中添加高性能炸药材料，基于JWL状态方程进行运算，模拟浅埋隧洞爆破振动效应，验证了电子雷管微差控制爆破的减振效果；叶宇等利用MIDAS/GTS-NX研究了相对位置不同的下穿隧洞爆破施工对挡墙和路基的振动规律[6]，为挡墙加固提供了有效信息。

本文结合宁波输水浅埋隧洞下穿公路(经寿山禅寺、寿峰寺段)工程，提出了控制爆破方案，其次，通过数值模拟采用三角等效荷载的加载方式模拟了爆破振动效应，并评价了控制爆破方案的安全性。最后由现场监测数据佐证实施方案的控制爆破效果及数值模拟预测评价的可行性，并拟合萨氏公式反映了输水隧洞爆破开挖影响下建筑物地表振动衰减规律，为后续的施工和相似工程提供借鉴与参考。

1 工程概况

宁波至杭州湾新区引水工程(头部工程至兴慈五路段)位于浙江省宁波市中北部，输水主线长69.3 km，主要建筑物由隧洞、管道、调节站、沿线阀井及附属设施等组成。本项目整体上基本呈南北向展布。地貌属侵蚀-剥蚀丘陵、山麓沟谷、冲海积平原，场地内地形复杂。主洞隧洞岩层主要为侏罗系西山头组(J3b)熔结凝灰岩；地表标高22～96 m，基岩为侏罗系上统高坞组流纹质晶屑熔结凝灰岩，为III级围岩，渗透性较差，洞身稳定性良好。

引水工程主隧洞在输8+798.099～输9+321.24段将紧邻古建筑施工，距寿山禅寺和寿峰寺的水平距离分别为50 m和100 m，如图1所示。为了减少隧洞爆破有害效应对寿山禅寺、寿峰寺主体建筑物产生不利影响，需要针对相应工程段进行控制爆破。

图 1 隧洞线路Fig. 1 Tunnel route map

2 控制爆破方案

2.1 炮眼布置

控制爆破范围总长度500.431 m，研究区域内均为III级围岩。隧洞爆破开挖采用全断面方法，隧洞断面为的底宽2.6 m×高3.2 m的割底马蹄形断面；炮眼直径为42 mm，根据设计轮廓线布置间距为50～70 cm的周边炮眼、间距为60 cm的辅助眼。采用直眼掏槽，并设置中心空眼。根据现场实际情况，结合式(1)得出炮眼取值，以达到最佳爆破效果

(1)

式中:q为炸药单耗量；r为线装药密度，2号岩石乳化炸药r=1 kg/m；η为炮眼装药系数，考虑到周边眼的布置，总眼数取36个(不含中空眼)，炮眼布置图如图2所示。

2.2 爆破参数设计

装药量的确定依靠公式(2)

Q=ηLr

(2)

式中:η为炮眼装药系数；L为眼深实际，取2.1 m；r为线装药密度，由公式(2)计算得到掏槽眼、辅助眼、周边眼和底板眼装药量分别为7.2 kg、14.4 kg、6.75 kg、4.8 kg。

现场采用直径为32 mm的2号岩石乳化炸药，单个药卷长度为200 mm，重150 g；掏槽眼、辅助眼采用连续装药，周边眼采用间隔不耦合装药，末端用炮泥堵塞，详细爆破参数如表1所示。起爆方式采用毫秒延期导爆管雷管起爆，导爆管连线为簇联法，装药顺序为先两侧后中间，并按照掏槽眼→辅助眼→周边眼→底眼的顺序微差起爆。

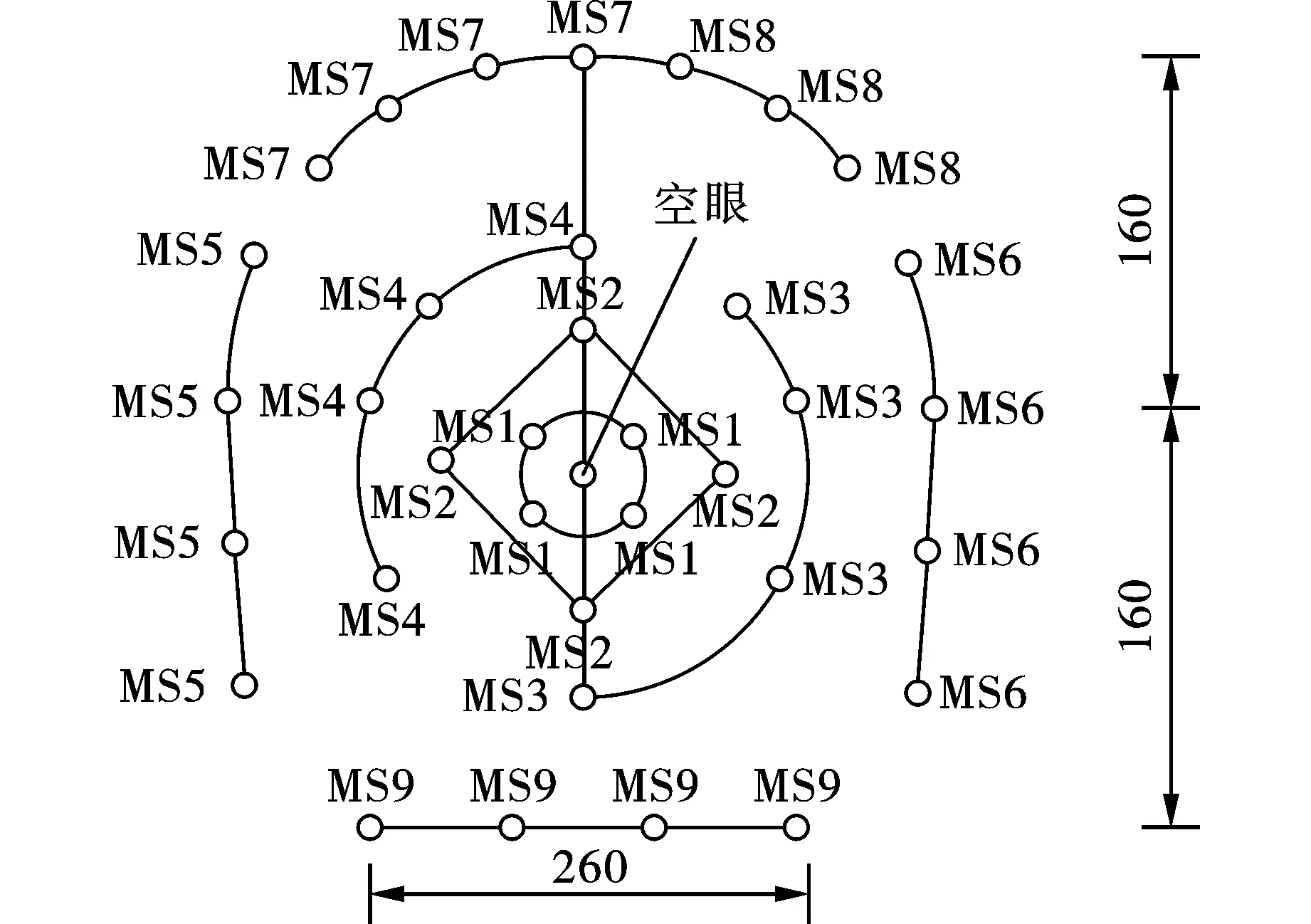
图 2 炮眼布置(单位：cm)Fig. 2 Hole arrangement(unit:cm)

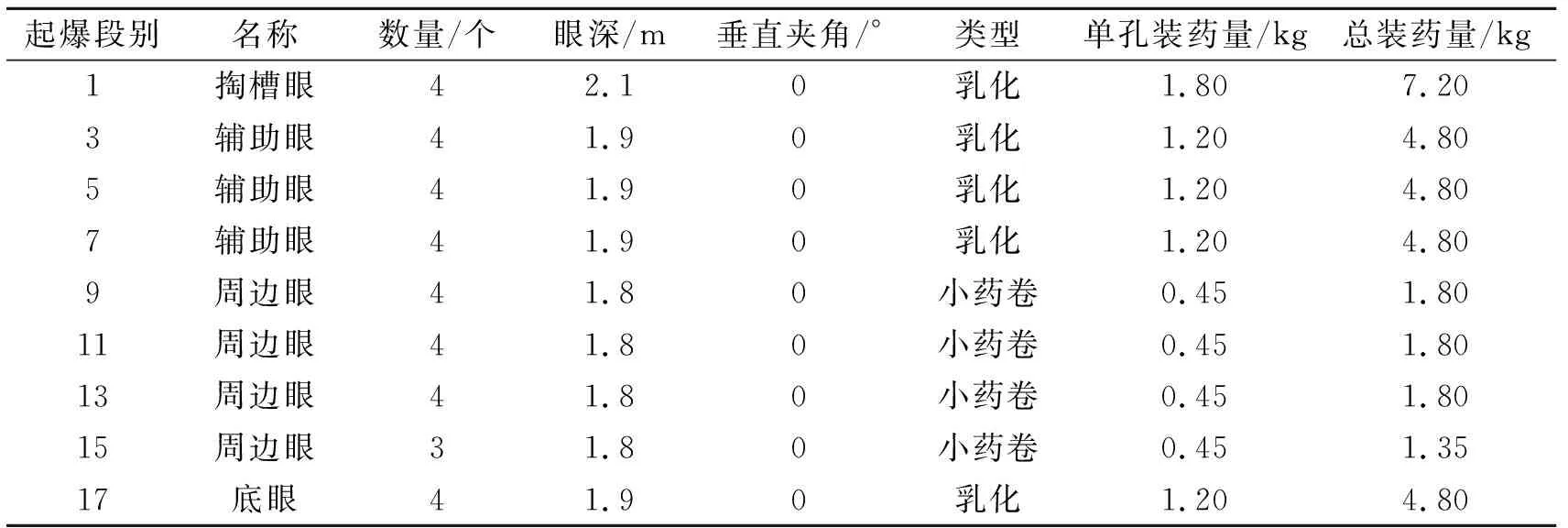
表 1 爆破参数

3 振动效应的数值模拟分析

3.1 模型建立

为研究上述控制爆破方案对紧邻建筑物的影响，通过surfer绘制了研究区域的等高线地形模型，精确展示出了隧洞周围的地形条件，如图3所示。将地形模型导入LS-DYNA软件中，模拟隧洞爆破开挖过程，分析得到隧洞爆破地震波对紧邻建筑物的影响。

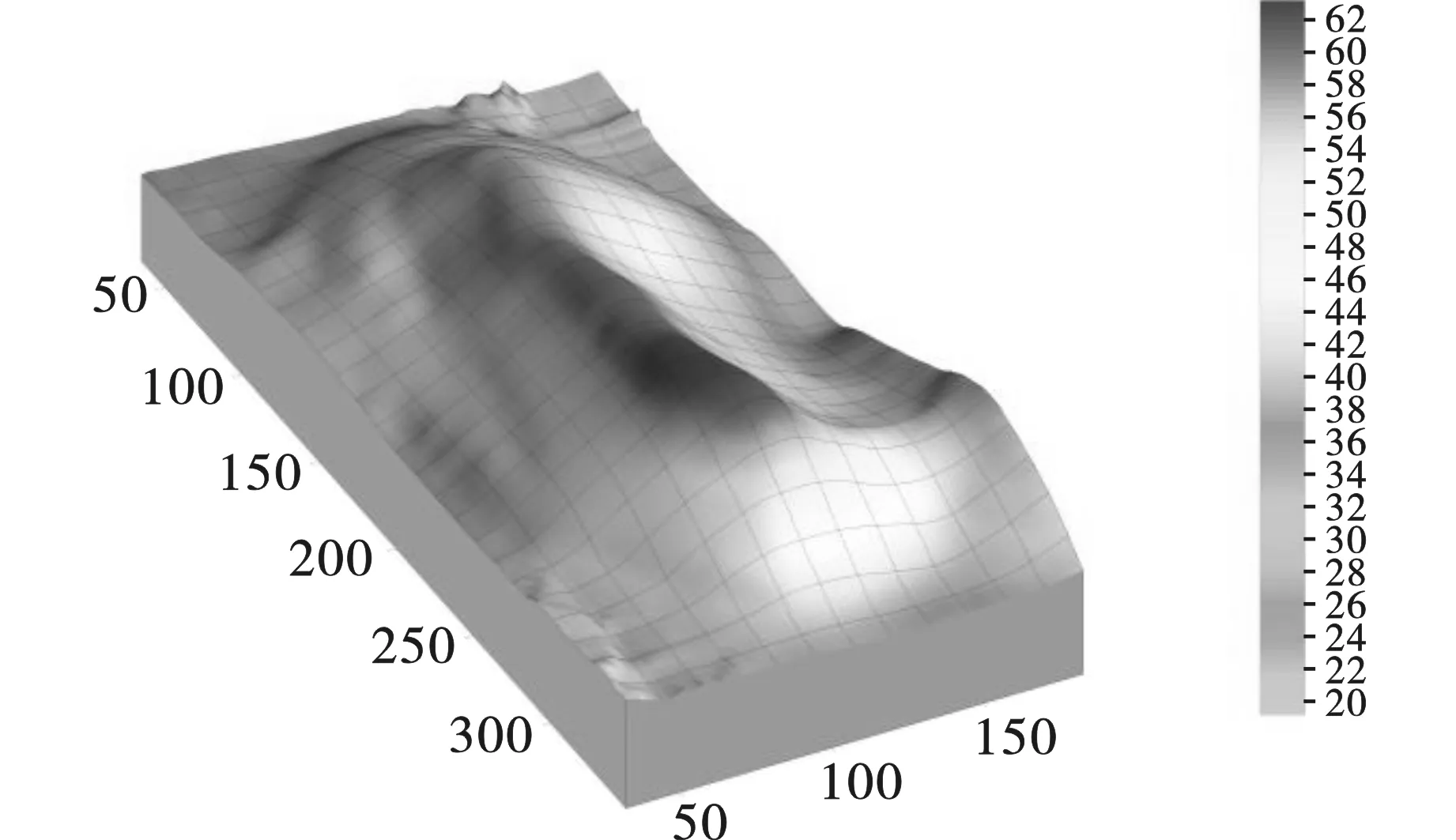
图 3 山体模型Fig. 3 The mountain model

建立的隧洞爆破动力有限元模型尺寸为30 m×100 m×50 m，其中隧洞断面为2.6 m×3.2 m，如图4所示。由于夹制效应的影响，掏槽眼的单段药量最大引起峰值振速，因此模型重点模拟掏槽爆破效应，掏槽眼爆破参数如表1所示。隧洞围岩采用非线弹性随动强化材料，参数如表2所示。模型采用SI国际m-kg-s单位制。

图 4 数值模拟模型Fig. 4 Numerical simulation model

3.2 动力荷载计算

采用炮眼壁上施加等效的三角脉冲荷载方法模拟爆破。根据圣维南弹性理论，将荷载施加在炮眼中心的连线上，不用考虑炮眼的形状[2]，如图5所示。荷载确定利用爆破荷载换算公式

P(t)=Pmf(t)

(3)

式中：Pm为脉冲峰值，f(t)为时间滞后指数函数。在不耦合连续装药和C-J爆轰条件下，Pm可根据式(4)进行计算[7-10]

(4)

式中：ρe为炸药装药密度；D为炸药爆速；γ为炸药的等熵指数；dc为等效药卷直径；db为炮眼直径；η为爆轰气体碰撞孔壁时压力增大倍数。

为了简化表现衰减规律，f(t)计算可近似按照三角形处理，爆炸脉冲荷载时程曲线如图6所示。

表 2 岩体参数

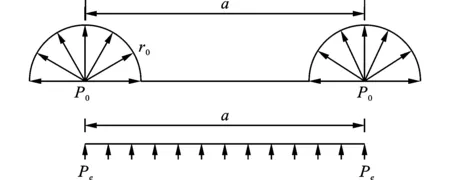
图 5 爆破荷载等效施加示意图Fig. 5 Equivalent application of blasting load

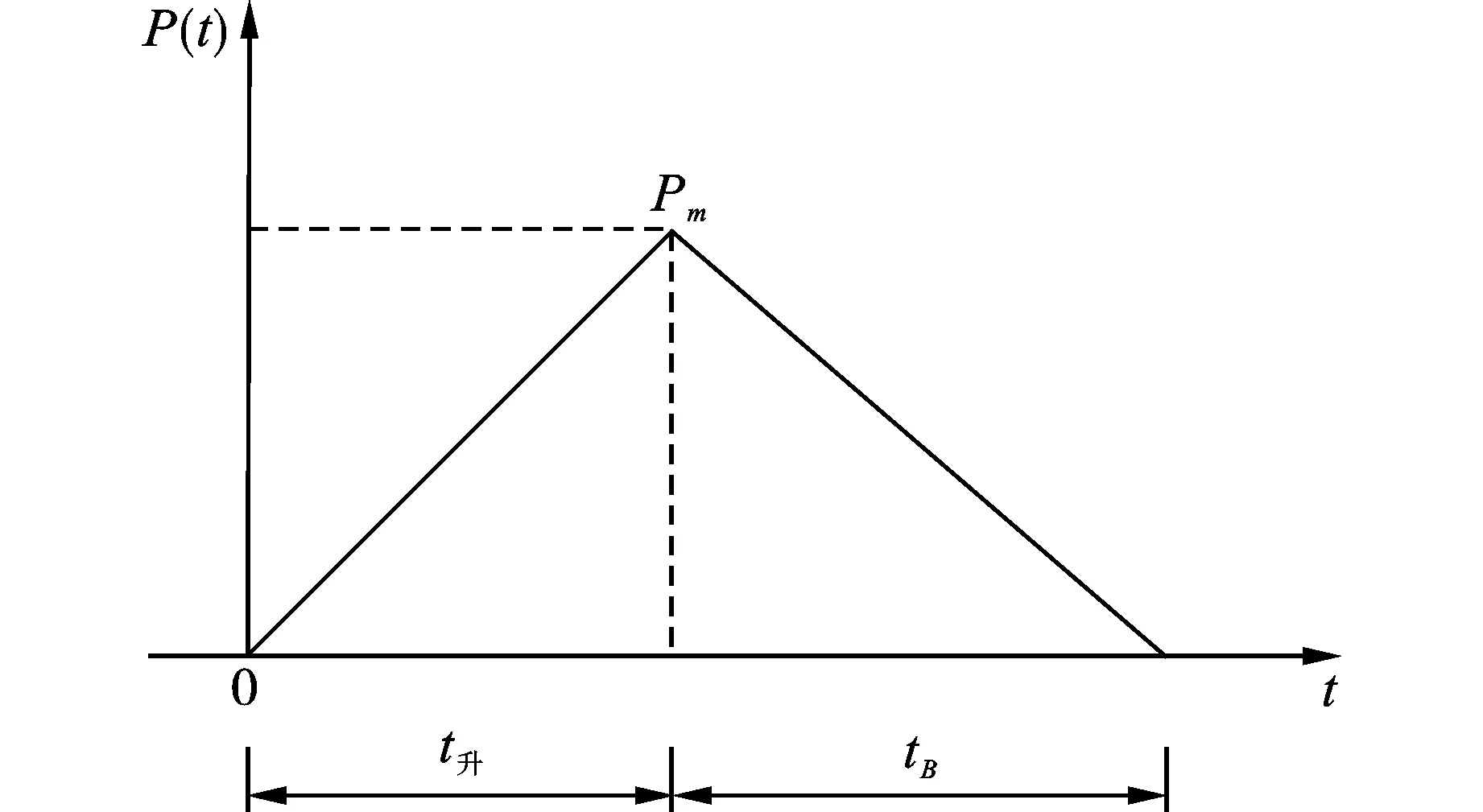
图 6 三角脉冲荷载作用时程曲线Fig. 6 Time history curve of pulse load

荷载与时间的关系表示为

(5)

爆破荷载的升压时间和正压作用时间由Zhan-Ping Song、陈士海等提出的公式(12-13)计算[11,12]

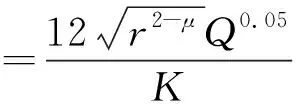
(6)

(7)

式中：K为体积模量，K=E/3(1-2μ)；μ为岩体的泊松比；Q为炮眼的装药量，kg；r为耦合系数。

由上述理论公式支撑可得出本次模拟的三角等效爆轰峰值荷载，具体参数如表3所示；可得爆轰力峰值Pm=5.775e+6 Pa；升压时间t升=200 μs，tb=300 μs。

表 3 等效荷载计算参数

3.3 振动速度特征分析

为了分析隧洞爆破对寿山禅寺和寿峰寺的影响，分别在于实际情况相同点设置监测点。各监测点的振速时程曲线如图7～8所示，各方向峰值振速及合速度统计如表4所示。

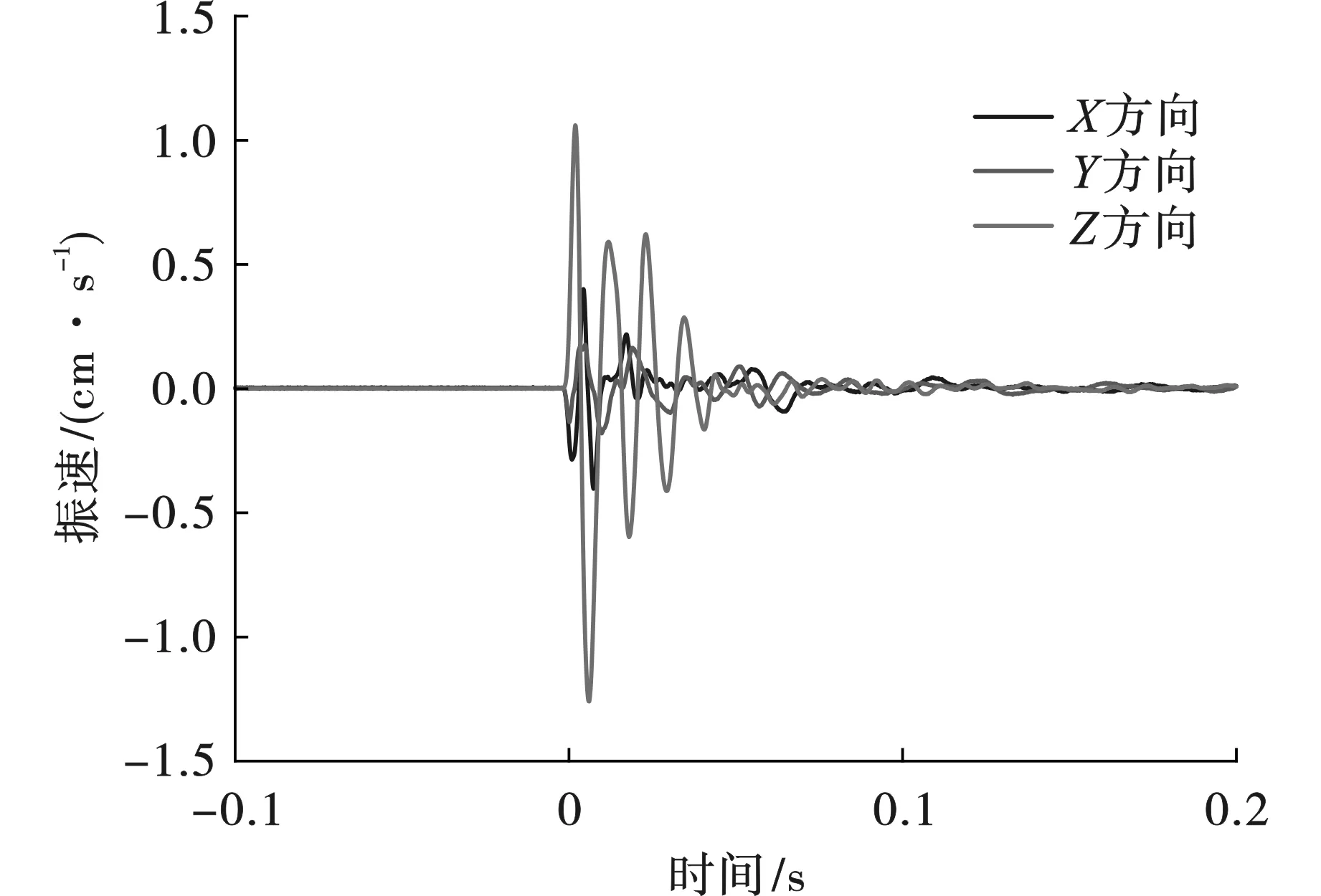
图 7 寿山禅寺测点振动速度Fig. 7 Vibration velocity in Shoushan Zen temple

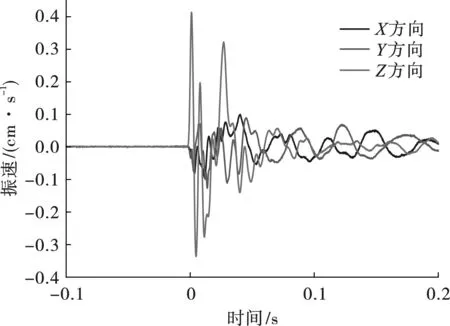
图 8 寿峰寺测点振动速度Fig. 8 Vibration velocity in Shoufeng

由表4可知，在隧洞爆破作用下，爆心距50 m处的寿山禅寺峰值约为1.04 cm/s，爆心距100 m处的寿峰寺振速峰值约为0.42 cm/s。根据爆破安全规程，两处寺庙的安全振速为2.5 cm/s，模拟结果表明隧洞爆破对两处建筑物影响较小，爆破振动均处于安全振速范围内。由图7～8可知，由于爆区岩体介质以应力波形式传播扰动，介质中的部分单元产生塑性变形，传播过程经历进入塑性区单元数量的增加[13]，随着时间的递增、传播距离增大振速不断降低。此外，垂直方向的振速(Z方向)大于径向(X方向)和纵向(Y方向)，这是由于在浅埋中远区入射纵波与竖直方向的夹角及爆心距共同作用导致的结果。

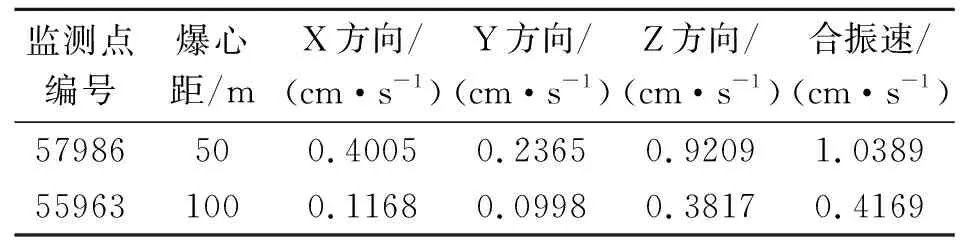
表 4 质点峰值振速

通过上述分析，可知拟定的控制爆破方案对既有建筑物的振动影响较小；虽然掏槽部分需要克服围岩的夹制作用所造成的振动较大，但峰值振动速度仍然处于规范要求的安全界限内，满足爆破安全要求。

4 爆破振动监测分析

4.1 测点布置

为了进一步论证数值模拟方案对预测振动模拟的可行性，对下穿既有建筑物隧洞爆破施工进行监测，将监测信号与数值模拟结果进行对比。结合现场情况，采用TC-4850高精度爆破测振仪对被保护建筑物角点地表进行振动监测，寿山禅寺布置监测点D1，寿峰寺布置监测点D2，如图9所示。

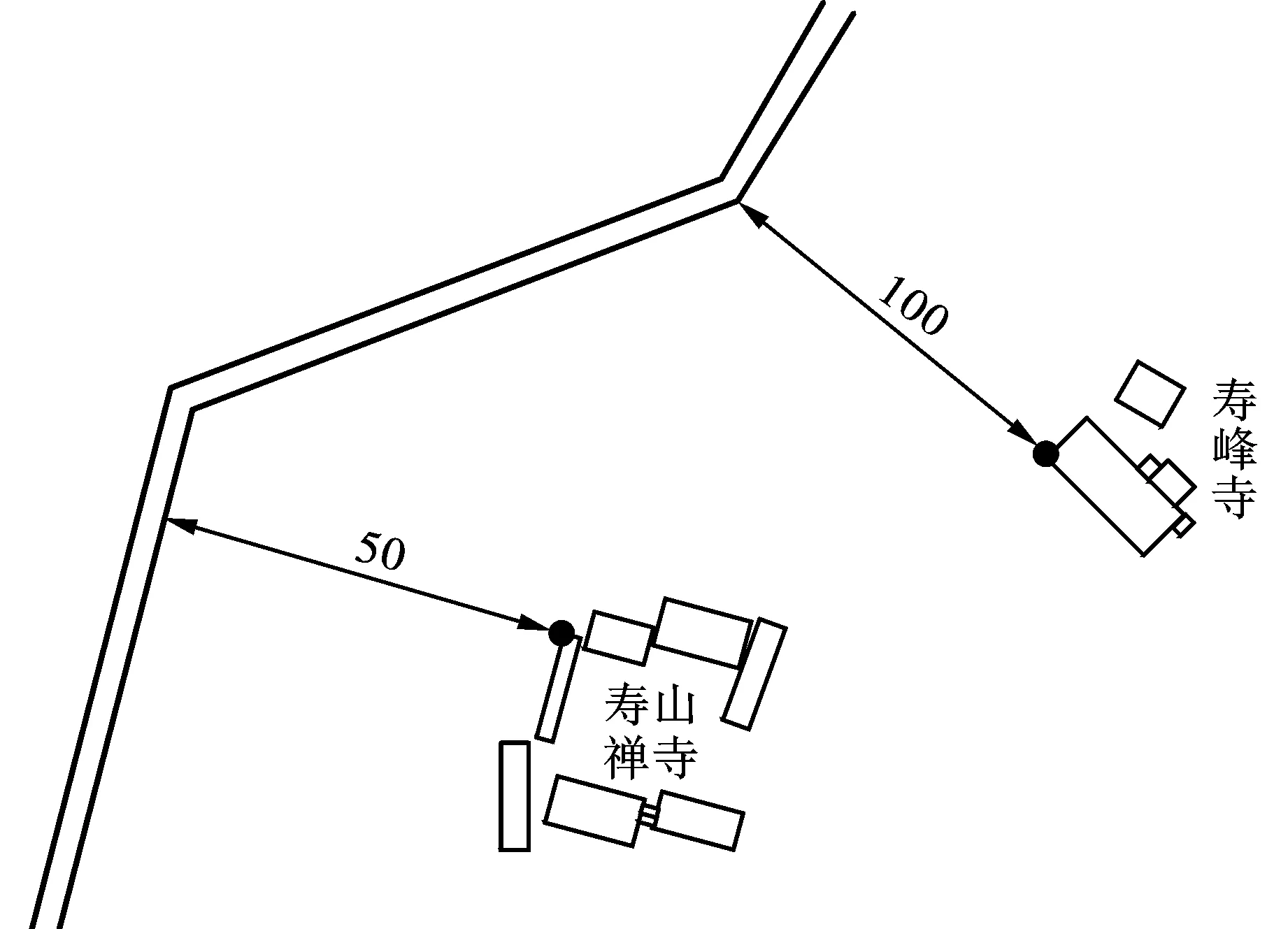
图 9 监测布点(单位：m)Fig. 9 Monitoring placement(unit:m)

4.2 振动监测结果分析

共进行了7次爆破监测，寿山禅寺布置监测点D1和寿峰寺布置监测点D2获得的实测典型振动如图10～11所示。

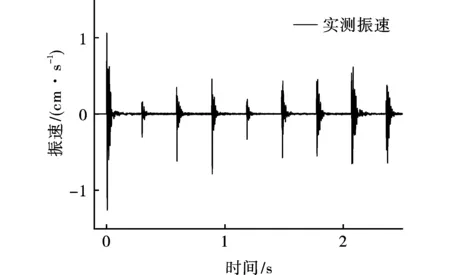
图 10 寿山禅寺实测振速Fig. 10 Shoushan Zen temple monitoring vibration velocity

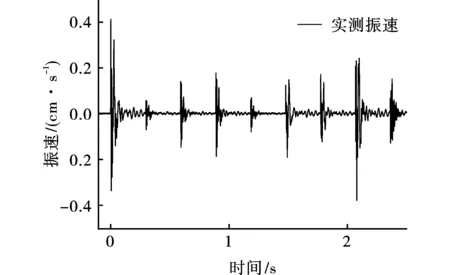
图 11 寿峰寺实测振速Fig. 11 Shoufeng temple monitoring vibration velocity

由图10～11可知，隧洞爆破作用下寿山禅寺实测峰值振速为1.01 cm/s，与模拟结果相差0.03 cm/s，误差为3.7%；寿峰寺实测峰值振速为0.41 cm/s，与模拟结果相比误差为2.3%。说明实测结果与模拟结果较吻合，考虑到工程地质条件的复杂性及模拟的理想性等因数，在允许的范围内产生误差是合理的。爆破地震波到达地面时由于爆心距的不同，表现不同，随着距离的增加，由于岩体阻尼较大，岩土体介质对信号有一定的吸收作用，且岩体中的节理裂隙及软弱夹层的影响导致波传播过程产生能量损耗，使其振速不断衰减，监测点衰减规律与数值模拟具有很好的一致性；由图可知，由于采用了毫秒电子雷管，减少了波峰的叠加效应，具有良好的降振作用。

为了进一步分析衰减规律，对实测的14组数据采用萨氏公式进行非线性拟合，结果如图12所示。拟合系数R2=0.932，表明了具有较好的拟合精度，反映了输水隧洞爆破开挖影响下地表振动衰减规律。研究表明数值模拟方法预测振动效应是可行的，能够有效地评价隧洞爆破作用对建筑物的不利影响。综合数值模拟和现场实测结果，本工程采用的控制爆破方案能够有效地降低爆破对紧邻建筑物的地震效应，确保建筑物稳定和输水隧洞施工的顺利进行。

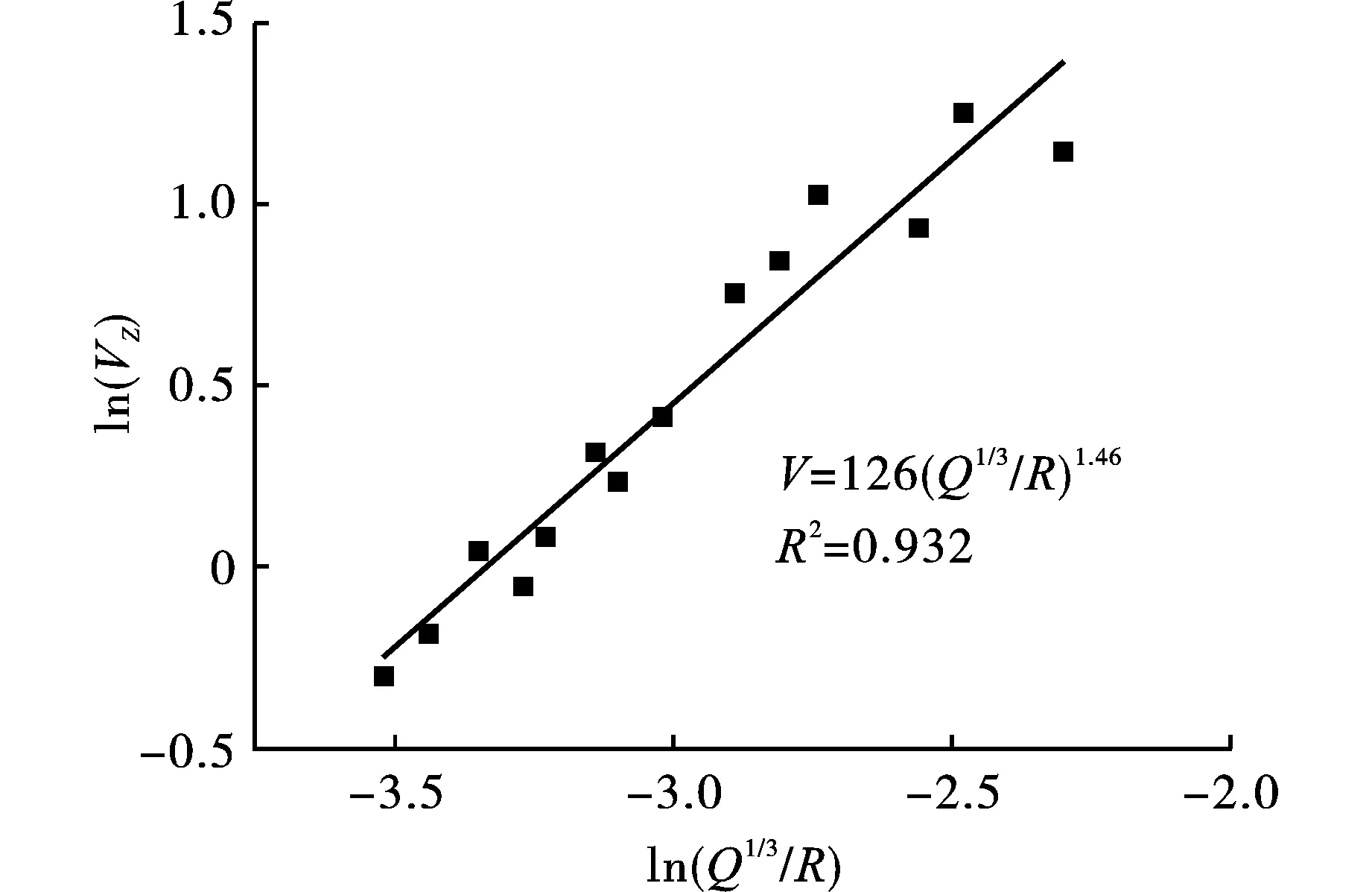
图 12 峰值振速拟合曲线Fig. 12 Fitting curve of vibration velocity

5 结论

通过对宁波至杭州湾引水工程主洞隧洞下穿公路(经寿山禅寺、寿峰寺段)控制爆破方案的研究分析可得到以下结论：

(1)有限元模拟分析表明，拟定的控制爆破方案是安全可行的，爆破振速峰值满足爆破规程安全范围(<2.5 cm/s)，地震波在介质中传递时，由于塑性区单元的作用，振速随着时间推移及爆心距的增加而不断衰减；三向振速中，垂直方向引起的振动效应最明显，振速峰值最大，这是浅埋中远区入射纵波与竖直方向的夹角及爆心距共同作用导致的结果。

(2)根据现场监测结果分析，对比可知数值模拟的振速峰值及衰减规律均与监测结果具有一致性，寿山禅寺和寿峰寺振速峰值误差分别为3.7%、2.3%，且由于岩体阻尼较大对信号具有一定的选择吸收作用，信号在岩体中传递的过程产生能量损耗，振速不断衰减，两者结果较吻合。

(3)基于监测结果进行萨氏公式回归分析，其拟合系数R2=0.932表明线性回归分析精确度高，反映了输水隧洞爆破开挖影响下地表振动衰减规律，进一步表明了数值模拟方法对提前预测振动效应具有可行性，结论为后续爆破施工方案设计提供参考借鉴。