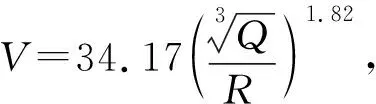充填体相邻采场低扰动爆破参数优化及应用*
2022-12-17张钦礼张雁峰安述庚张德明王道林
张钦礼,张雁峰,安述庚,张德明,王道林
(1.中南大学 资源与安全工程学院,长沙 410083;2.安徽开发矿业有限公司,六安 237400;3.湖南中大设计院有限公司,长沙 410000)
由于充填采矿法在安全回采及控制地压方面的优越表现,不同矿山因地制宜演变出契合自身矿体赋存性质的充填采矿方法[1]。其中,以大跨度高中段为主要特征的空场嗣后充填法,凭借其生产效率高、回采工艺简单、一次崩矿量大等优点,在围岩较为稳固的金属矿山得到广泛应用。例如冬瓜山铜矿采取隔一采一的回采顺序[2],矿房、矿柱宽均为18 m,采场最大高度超70 m。安庆铜矿采用两步骤回采方式[3],矿房矿柱宽度均为15 m,采场高度高达114 m。在二步回采过程中,充填体不仅受到上覆围岩的静载荷压力,还会受到二步回采时爆破振动产生的动载荷影响。因此为降低爆破扰动,一般会在临近充填体一侧设置一定厚度的矿体保护层,但根据“应采尽采”的资源回收原则,保护层厚度设置过大会造成不必要的矿产资源浪费,过小又起不到降低爆破扰动的作用。目前,在保证充填体强度的基础上,通过优化保护层厚度、炸药单耗、起爆方式等手段降低爆破作业对充填体的动力学扰动,是保证充填体稳定性,提高矿山安全生产水平的关键举措。刘优平等采用LS-DYNA分析凡口铅锌矿间柱采场近充填体炮孔的爆炸应力场[4],对比分析充填体内一系列节点的振动速度,以优化炮孔装药结构,从而控制爆破对充填体的影响。文兴等利用阿舍勒铜矿现有微震监测系统[5],对于现场爆破振动进行测试并计算优化现有爆破孔网参数,提高了二步骤采场的安全性;张金等通过分离式霍普金森压杆(SHPB)试验获得矿石和充填体的动力学参数[6],并以此利用LS-DYNA对不同孔底距、排间距等多种方案的充填体响应进行模拟分析,得到了能够对应满足充填体稳定性且爆破效果最佳的方案。朱瑞鹏等通过分析爆炸应力波在胶结充填体内部空隙中的透反射规律[7],建立了充填体张拉破坏理论模型,为胶结充填体在二步回采中稳定性分析提供了新的参考依据。姜立春等采用弹性力学半逆解法[8],建立边界力耦合作用下胶结充填体的临界爆破振速相对于充填体灰砂比、高度与宽度等尺寸因素之间理论模型。
研究者们针对爆破对充填体的影响及控制措施进行了大量研究,但研究方法相对较为单一,影响因素考虑不全面,且很难与现场实际工况相符。有鉴于此,以李楼铁矿二步回采对充填体的爆破扰动为研究对象,利用LS-DYNA软件构筑充填体-矿体-炸药三者耦合作用模型,获得不同保护层厚度及起爆方式下充填体的动力学响应规律,并通过现场工业试验对数值模拟结果进行验证。
1 工程概况
李楼铁矿矿床南北走向长约3.4 km,东西宽约500 m。矿体埋深90~341 m,斜深100~767 m,最大控制深度为-862 m标高,上覆农田。李楼铁矿采取分段凿岩阶段矿房法进行回采,一步采结束后进行充填,待充填体固结稳定后再进行二步回采(见图1)。每阶段矿房高100 m,分四个分段,每分段高度为25 m,凿岩巷道规格为4 m×4 m的正方形,布置于二步采的矿体底部,并从凿岩巷道向上钻扇形孔。爆破选用规格为80 mm的扇形孔,排距为1.7~1.9 m,边孔孔角为30°~40°,采取连续耦合装药,起爆方式采用孔底起爆及孔口起爆,如图2所示。根据现有爆破现场工况发现,进入二步回采后,相邻采场的爆破振动会造成充填体的边帮片落甚至大幅凹陷,进而影响回采率及充填体稳定性的生产难题。鉴于需要满足李楼铁矿500万t/a的产能刚需,很难对装药密度进行优化。因此,亟待开展不同保护层厚度下爆破对充填体的影响研究,进而确定安全、经济、合理的保护层厚度,为矿山的爆破设计提供理论支撑。

图 1 二步采爆破示意图(单位:m)Fig. 1 Schematic diagram of second-step mining and blasting(unit:m)
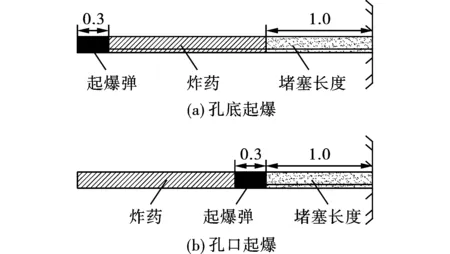
图 2 孔底起爆与孔口起爆装药示意图(单位:m)Fig. 2 Schematic diagram of bottom initiation and top initiation(unit:m)
2 爆破响应数值模拟
2.1 材料参数选取
2.1.1 炸药
在工程爆破中,定义炸药材料模型通常是在模型建立完毕后,通过修改K文件来设置炸药模型属性,对于不同的炸药,其密度以及JWL状态方程也有所不同[9]。本次模型炸药采用LS-DYNA常用的炸药材料模型“HIGH_EXPLOSIVE_BURN”模型以及JWL状态方程用来描述炸药的爆炸过程[10],JWL方程具体如式(1)。
(1)
式中:P为爆轰压力;V为相对体积;E为单位体积内能;其他均为炸药材料相关的参数。模拟采用2号岩石乳化炸药,具体参数如表1所示。

表 1 2#岩石乳化炸药材料模型主要参数
2.1.2 矿岩体与充填体

(2)
(3)
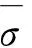
(4)
可以看出,弹性畸变能的大小和等效应力呈正相关。而根据李楼铁矿现场实际工况,爆破对充填体的破坏主要是产生的应力波在充填体内的传播造成的拉伸破坏,从而造成充填体呈片状或块状进行垮落,而非粉末状破坏,需结合充填体的极限拉应力对爆破影响区域进行分析。矿体与充填体模型采取LS-DYNA中的塑性随动材料“MAT_PLASTIC-KINEMATIC”,参考李楼铁矿具体的力学参数,矿体与充填体的材料参数如表2所示。

表 2 李楼铁矿矿体与充填体力学参数
2.2 破坏判据
炸药爆轰传播过程基本分以下几个阶段[13]:(1)爆破发生极短时间内,冲击波超过岩体动态抗压强度,将炮孔周围岩石压碎并扩大炮孔空间。(2)随时间推移,炸药爆炸产生的压力不足以压碎岩石,但当应力波产生的切向拉应力超过岩体抗拉强度时,仍能导致岩石产生拉伸破坏,这也是充填体受爆破影响最主要的破坏形式。结合Von Mises屈服准则,当模拟充填体单元所受有效应力大于充填体极限抗拉强度时,判定为失稳状态。
振速标准根据《爆破安全规程》(GB6722—2014)规定[14],二步采生产过程中充填体单元受爆破振动影响的峰值振速不得超过12 cm/s。
充填体合位移标准根据过往研究的等效破坏原则结合李楼现场工况所定,当充填体单元合位移值处于0.1~0.3 mm时,即认为该位置上的单元受到较大影响或较小损伤。后续模拟方案中充填体稳定性分析将综合考虑以上标准来开展研究。
2.3 建立数值模型
以扇形炮孔中心剖面与沿凿岩巷道方向为对称面,建立1/4大小的模型(见图3)。二步采爆破模拟结构模型共分为4个Part:炸药、ALE虚拟空间,矿体和充填体,其中ALE虚拟空间在模拟中仅用于炸药传递爆破冲击力于矿体中。炸药与虚拟空间采用ALE算法,矿体与充填体采用Lagrange算法。计算模型采用单元类型为三维实体solid164,模型计算尺寸为35 m×2 m×25 m,充填体长度为20 m,矿体长度为15 m,分段高度为25 m,厚度为2 m。二步采炮孔为上向扇形孔,炮孔直径为80 mm,单排起爆。模型的上、下,左,后表面通过关键字Non-Reflection-Boundary施加无反射边界约束,在模型的右边与前边设置对称条件,单位采用cm-g-μs。结合李楼铁矿二步采实际生产状况,分别对孔底起爆与孔口起爆时,四种保护层厚度(0.5 m、1 m、1.5 m、2 m)下爆破作业对充填体的影响进行分析。
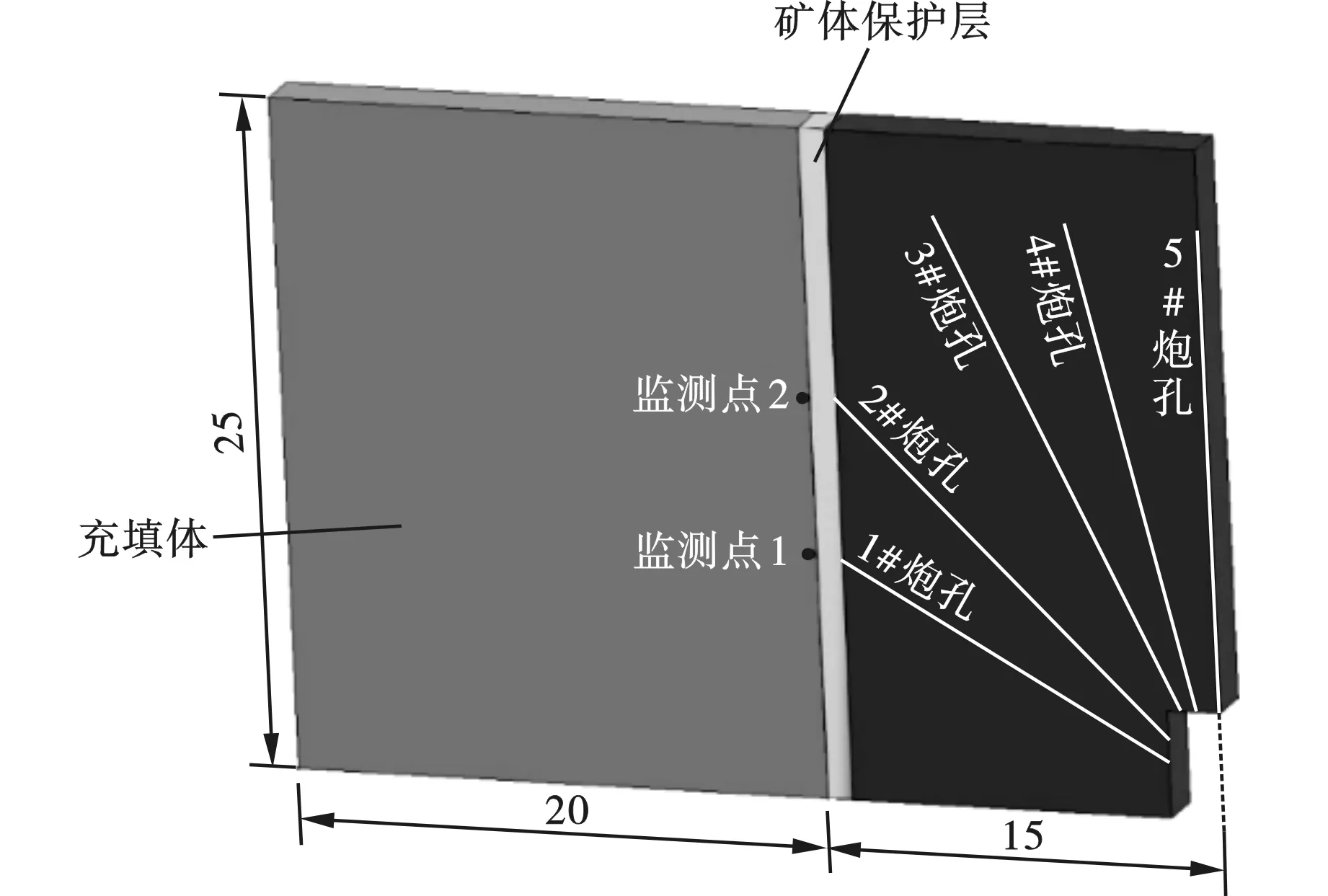
图 3 二步采爆破模拟结构模型建立(单位:m)Fig. 3 Second-step mining and blasting simulation structure model establishment(unit:m)
3 基于LS-DYNA的保护层厚度优化
运行后处理软件LS-PREPOST对不同方案模拟结果进行读取并进行分析。以充填体抗拉强度为上限,分别提取孔底起爆方案与孔口起爆方案应力云图于图4与图5。
应力云图显示,在两种起爆方式下,距离炮孔最近的充填体边界部位所受应力波影响都最为显著,而其他边界部位受应力波影响较小,其原因是充填体本身性质可以被视为软岩,反射能力强,高应力波抵达充填体边界处时会快速扩散。同时,随保护层厚度的增加,应力波传播至充填体所需时间更长,充填体内部受影响深度也越小。若以充填体抗拉强度为上限,在孔底起爆方式下保护层为0.5 m的模拟方案中充填体内部受应力波影响深度将近1.5 m,而在保护层为1.0 m的方案中则缩减至0.6 m,直观反映出了保护层的设置对于充填体的保护作用;而当采取孔口起爆方式时,保护层厚度为0.5 m的方案充填体内部受影响范围仅为0.3 m,相对于孔底起爆同保护层厚度方案而言,孔口起爆产生的应力波传播需要更长时间,衰减程度更大。
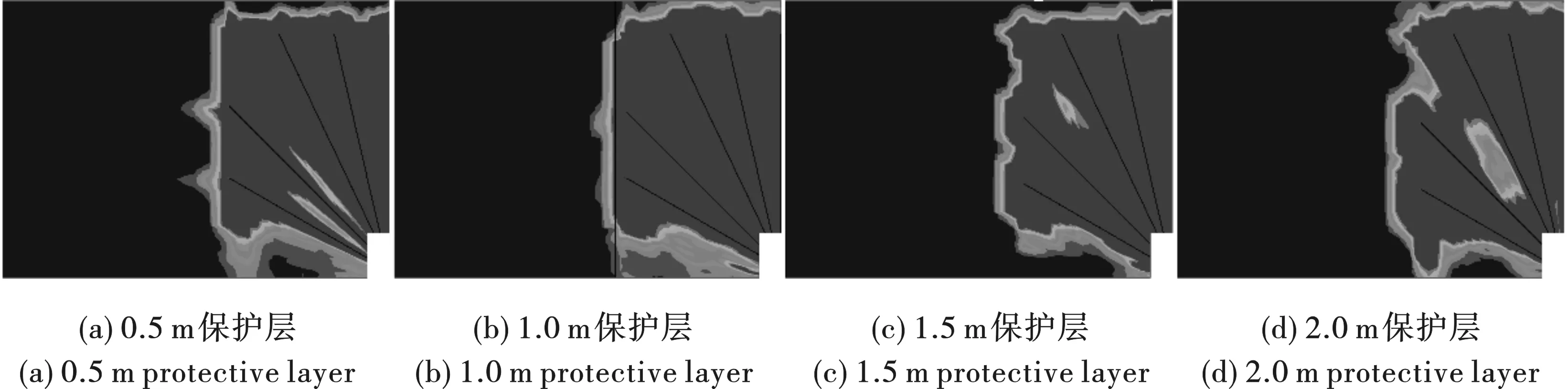
图 4 孔底起爆模拟方案等效应力云图分布Fig. 4 Equivalent stress cloud distribution of bottom-hole initiation simulation scheme
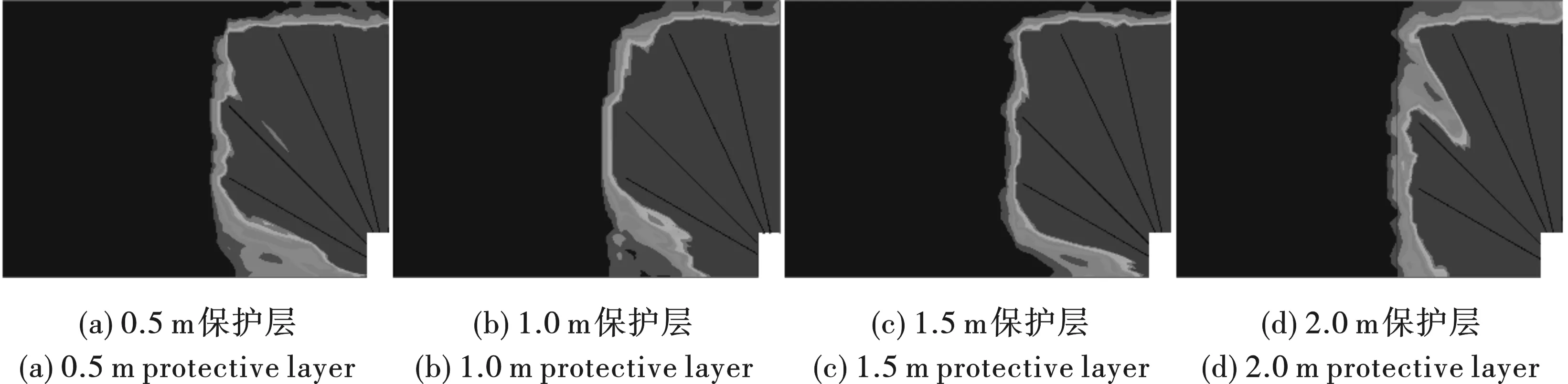
图 5 孔口起爆模拟方案等效应力云图分布Fig. 5 Equivalent stress cloud distribution of top-hole initiation simulation scheme
为研究爆破对于充填体的具体影响,作不同模拟方案充填体与矿体交界面的等效应力云图于图6与图7,并对模型按照XZ方向镜像得到1/2模型。如图,不同方案中应力波在交界面上的传播均呈现出球形扩散,距离1#、2#炮孔最近的单元处于球心位置,且所受应力波影响最为显著。因此,选取距离1#炮孔最近的单元26635(测点1)以及2#炮孔最近的单元30415(测点2)作为监测点(如图3所示),记录并分析两测点的等效应力、振速、合位移在不同时刻下的变化,从而对模拟方案中的充填体的稳定性做出评价。

图 6 孔底起爆模拟方案充填体交界面等效应力云图分布Fig. 6 Equivalent stress cloud distribution of filling body interface in bottom-hole initiation simulation scheme

图 7 孔口起爆模拟方案充填体交界面等效应力云图分布Fig. 7 Equivalent stress cloud distribution of filling body interface in top-hole initiation simulation scheme
图8与图9为不同起爆方式下保护层厚度设置为0.5 m时,监测点单元所受等效应力、合振速以及合位移时程曲线。采用孔底起爆时,最大等效应力为0.44 MPa,峰值振速为59.02 cm/s,最大等效位移为0.21 mm,均出现于单元30415(2#测点),远超充填体相应稳定判据;当采用孔口起爆时,监测点各项指标均小于孔底起爆方案,其中,最大等效应力为0.26 MPa,略低于充填体抗拉强度,但峰值振速为44.97 cm/s,仍高于充填体稳定振速标准。对图8中2#测点(单元30415)应力时程曲线(见图1-a)进行分析:在爆破开始后第2 ms左右,1#炮孔爆破产生的应力波抵达2#测点,并在充填体边界处发生扩散,在图中表现为等效应力迅速上升至峰值0.44 MPa,然后快速衰减至0.10 MPa;随后,其他炮孔爆破产生的应力波同样传递至充填体边界,导致等效应力再度攀升,但并未超过前峰;随着应力波在充填体内部的折射与衰减,2#测点所受等效应力逐渐震荡衰减,最终呈现出稳定趋势;从振速时程曲线来看,监测点峰值振速与峰值应力出现时间点相对应,且监测点的等效合位移时程曲线走势与等效应力大致相同。同时,虽然1#测点(单元26635)的爆破响应特征曲线与2#测点相类似,但由于距离其他炮孔较远,其等效应力、振速以及合位移的峰值均低于2#测点对应值。
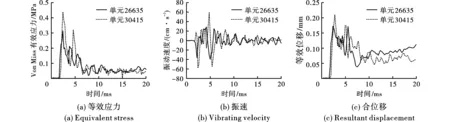
图 8 0.5 m保护层孔底起爆方案监测点特征时程曲线Fig. 8 Characteristic time-history curve of monitoring point of 0.5 m protection layer bottom-hole initiation scheme

图 9 0.5 m保护层孔口起爆方案监测点特征时程曲线Fig. 9 Characteristic time-history curve of monitoring point of 0.5 m protection layer top-hole initiation scheme
监测点单元在不同起爆方案下随保护层厚度的爆破响应特征变化趋势见表3。当选用孔底起爆方式,保护层厚度增至1.0 m时,监测点单元峰值振速由72.68 cm/s降至28.68 cm/s,降低了约60.6%,但仍高于充填体允许最大振速;最大有效应力则从0.44 MPa降低至0.12 MPa;最大合位移则降低较小,仅降低0.02 mm。当保护层厚度为1.5 m时,监测点峰值应力低于充填体抗拉强度,且等效位移仅为0.10 mm,峰值振速也小于《爆破安全规程》(GB6722—2014)中的充填体最大允许振速12 cm/s,可以认定此时监测点单元处于安全稳定状态。此后,当保护层厚度继续增加时,充填体稳定性得到进一步加强,然而过厚的保护层厚度会使得矿体的回收率变差,对实际生产经济而言会产生负面影响,同时,相应峰值应力、振速以及合位移指标降幅较小,对充填体稳定性增益不大,因此,采用孔底起爆方案时最佳的保护层厚度为1.5 m。对孔口起爆而言,当保护层厚度增至1 m时,监测点所受最大有效应力已降至0.03 MPa,同时,最大振速相对降幅更大,从44.97 cm/s降至9.35 cm/s,合位移也降至0.07 mm,各项指标均在充填体安全范围内,可以判定此时充填体已处于稳定状态。因此,对于孔口起爆方案只需设置保护层厚度为1.0 m即可保证二步回采的安全进行。相对于孔底起爆方式的1.5 m保护层厚度而言,减小了1/3的保护层厚度,对二步采矿石回收而言具有更大的增益。
4 现场工业试验
模拟结果显示,采用孔口起爆,保护层厚度设置为1.0 m的爆破回采方案不管是充填体的稳定性还是矿石的回收率都能够得到有效的改善。为验证模拟结果,选取李楼铁矿某二步回采矿房进行现场工业试验。
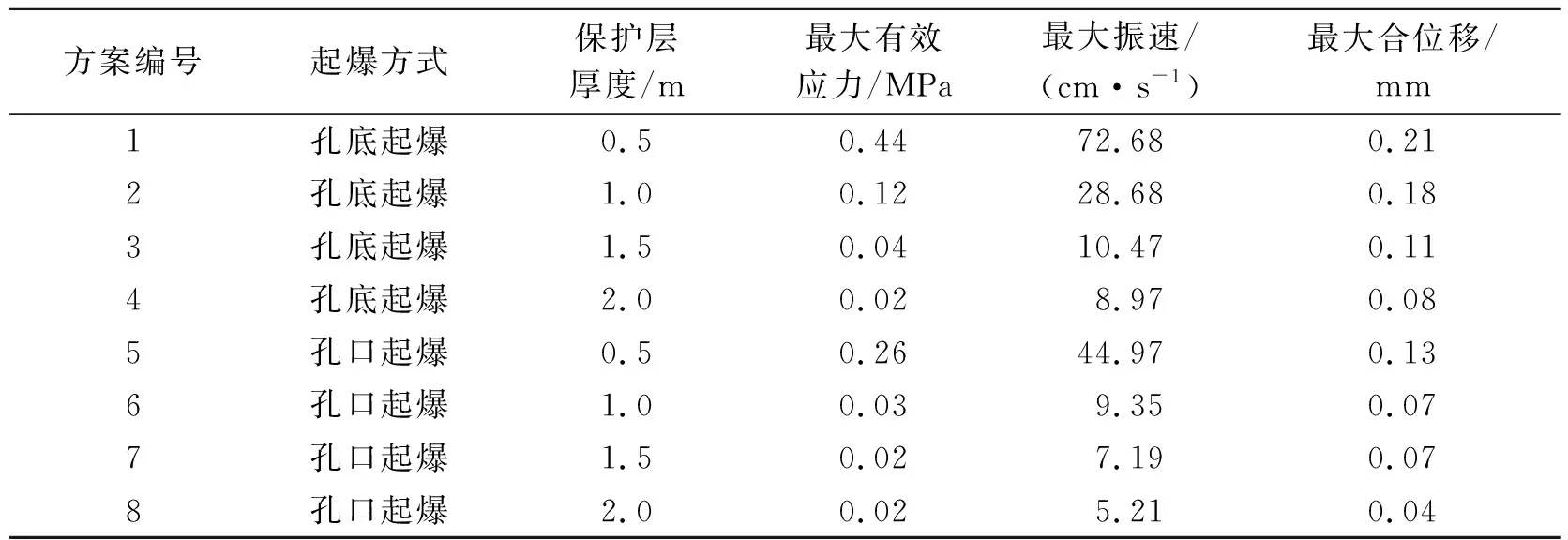
表 3 不同模拟方案监测点爆破响应特征
在现场爆破过程中,由于充填体内部应力与位移较难监测,因此在二步采场侧帮充填体的相邻位置安装微震测振仪,在爆破回采时记录相关振速数据后,再通过回归分析获得振速与距离的规律公式并推算出充填体质点振动速度,从而与数值模拟对应结果互相印证。振动速度采用iSV-420型一体化测振仪进行测量,集三轴向振动传感器和数字化测量、存储、无线传输于一体,如图10所示。为保护仪器,在距离起爆位置27 m、30 m、32 m、34 m处布置4个测点,分别为1#~4#测点,具体布置位置见图11,二步采矿房炮孔布置图如图12所示,保护层厚度设置为1.0 m,采用单段孔口起爆方式,装药密度与模拟方案选用一致,单段药量为400 kg。

图 10 iSV-420型一体化测振仪Fig. 10 iSV-420 Integrated Vibration Tester

图 11 爆破位置及爆破振动仪安装位置俯视图(单位:m)Fig. 11 Top view of blasting position and installation position of blasting vibrator(unit:m)
爆破完成后,将测振仪所采集到数据通过无线信号传输至计算机中并导入测振仪配套软件拓普测控imsServer,得到三向峰值振速。由于X向振动速度与采场走向垂直,与充填体相对采场方向一致,因此取其峰值振速进行萨道夫斯基公式进行回归[15,16]。4个测点的相关监测数据如表4所示。
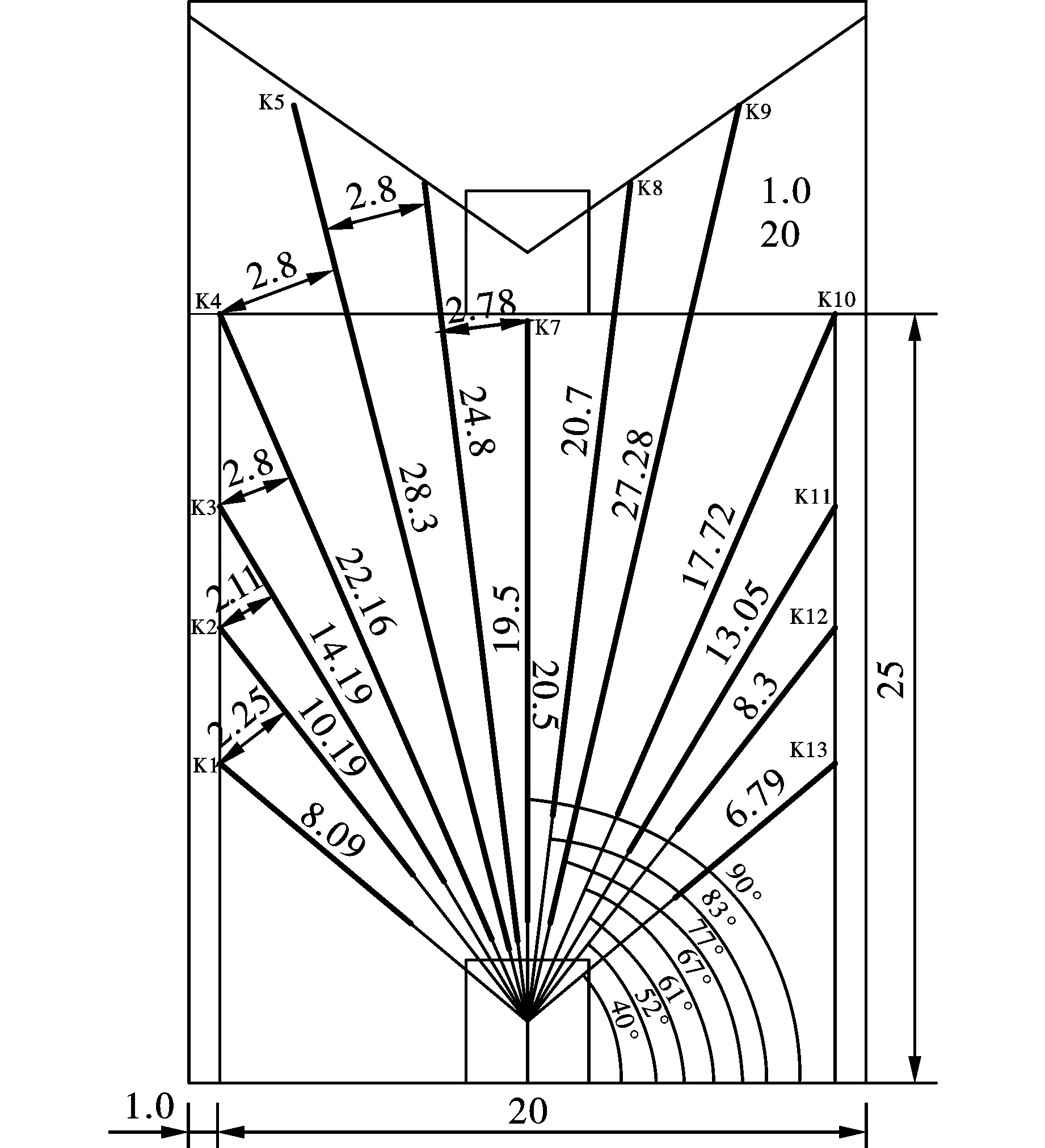
图 12 现场工业试验孔口起爆方案炮孔布置图(单位:m)Fig. 12 Layout of blast hole in field industrial test top initiation scheme(unit:m)
萨道夫斯基公式见式(5)。
(5)
式中:V为监测点最大振速,cm/s;Q为单段爆破药量,kg;R为爆心距,即爆破点到监测点的直线距离,m;K与α分别为与环境条件相关的衰减指数。在式(5)两边取对数得式(6)。
(6)
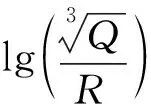
(7)
采场中充填体监测点与爆心的距离为L=15 m,代入萨道夫斯基公式7计算得峰值振速V=9.37 cm/s,与模拟所得结果基本一致。

表 4 不同测点X向爆破振动速度峰值与爆心距对应表格
图13为爆破后现场照片,从照片上可以清晰地看到采场侧帮裸露出充填体,且整体完好,基本无损伤,而崩落的矿石块度较为均匀,大块较少,爆破效果较好。因此,从现场工业试验来看,数值模拟结果与实际生产结果相对吻合,利用LS/DYNA软件进行数值模拟对于研究充填体受爆破扰动稳定性具有可行性。

图 13 爆破后采场与崩落矿石现场照片Fig. 13 Photographs of stope and caving ore site after blasting
5 结论
运用LS-DYNA软件对李楼铁矿二步回采过程中充填体爆破响应特征进行数值模拟并对结果进行分析,并通过现场工业试验对模拟结果进行验证,得到以下结论:
(1)二步回采过程中,爆破对于充填体的影响主要集中于充填体的边界处,若充填体失稳,将首先从距离炮孔最近的部位产生破坏,且其破坏形式为拉伸破坏。
(2)模拟结果显示,对于孔底起爆而言,保护层厚度需设置1.5 m才能保证充填体的稳定性,而对于孔口起爆而言保护层厚度缩减至1.0 m,从而增加矿石回收率,同时保证充填体单元有效应力,振速以及位移处于安全范围内,为充填体稳定性提供保障。