基于问题驱动的“以学生为中心”的矩阵乘法教学设计研究

李艳艳，蒋建新，高美平，黄卫华

（文山学院人工智能学院，云南 文山 663099）

《线性代数》课程是理、工、农、经管类专业必修的基础数学课之一，关于线性代数的课程建设、教学改革，以及教学设计等，已经进行了各具特色的研究。

本文把研究视角放在具体的一节课的教学设计研究上，从小视角见大问题。矩阵乘法选自线性代数第二章第2节矩阵的运算部分，矩阵是线性代数问题的主要工具，矩阵乘法是矩阵的重要运算，不管是对于后续知识的学习，还是实际的应用，都发挥着承前启后和不可替代的作用。本文着重从理论角度、实践应用角度、课程思政角度、学生中心角度研究矩阵乘法的教学设计问题。

1 预备阶段

1.1 教材分析

矩阵与矩阵的相乘运算是矩阵中常用的运算，是学习矩阵的逆、矩阵的对角化等本课程后续内容的基础，通过本节的学习，要求复述矩阵的乘法运算规则，应用矩阵的乘法运算满足的规律解决问题。特别地，要识记矩阵乘法运算不满足的规律，认识左乘和右乘的概念。

1.2 学情分析

学生已经掌握了矩阵的概念，掌握了矩阵的加法运算和数乘运算，矩阵的加法是两个矩阵相加，要求相加的两个矩阵是同型矩阵。那么两个同型的矩阵是否也可以相乘呢？运算规则是什么？带着这些问题，学习矩阵的乘法运算。

1.3 教学目标

（1）复述两个矩阵相乘C=AB的运算中，必须满足前一个矩阵的列数等于后一个矩阵的行数才可以相乘，掌握乘法运算法则。

（2）识记矩阵乘法运算不满足的规律，深入理解矩阵的概念。

（3）灵活、熟练利用矩阵乘法解决矩阵运算的问题。

1.4 教学重点

（1）两个矩阵相乘C=AB的运算法则中，前提条件、结果类型、乘积之后元素的特点。

（2）矩阵乘法运算与实数域中两个实数乘法的差别，矩阵乘法运算不满足交换律和消去律。

1.5 教学难点

（1）矩阵乘法的运算规则。

（2）矩阵乘法不满足的规律。

2 从理论角度的教学设计

目前文山学院使用的线性代数教材是同济大学工程数学——线性代数，贯穿教材的主线是求解线性方程组，重要载体是矩阵，那么矩阵运算的学习就显得尤为重要。矩阵乘法不像实数乘法那样直接，但又关联度紧密。为了使该问题的认识能更加自然和深刻，所以采用了从具体到抽象，从特殊到一般的设计思路，以及类比的数学思想方法。

2.1 从具体到抽象

通过工厂总收入和总利润问题的简便解决，探究矩阵乘法法则，然后将该法则从具体抽象到一般情况。

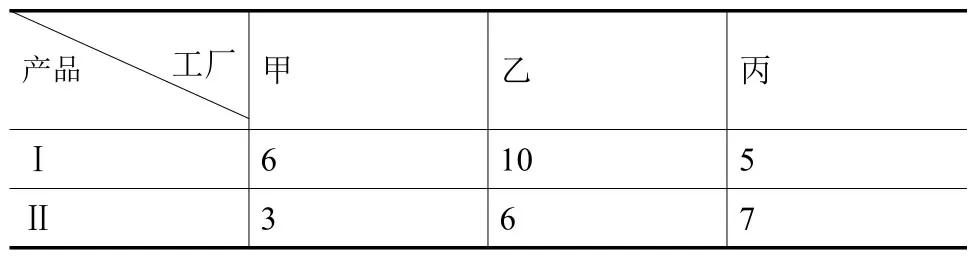
表1 2017年各工厂的各产品产量（吨）

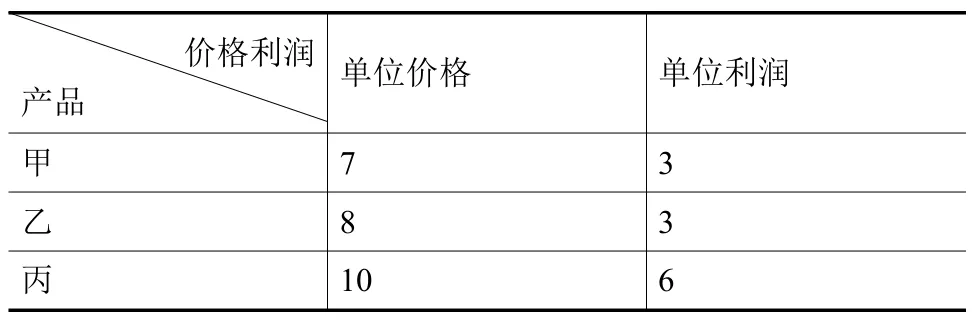
表2 各产品的单位价格及单位利润（万元/吨）

表3 各工厂一年的总收入及总利润（万元/吨）

将上述3个表格分别抽象成矩阵

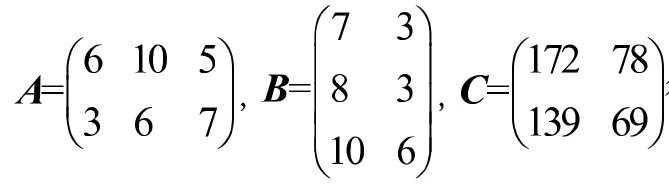
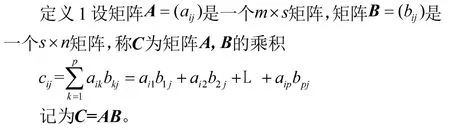
2.2 从特殊到一般

矩阵乘法的性质，与传统认知中的实数乘法有着一定的差异和相似，所以在第一阶段基础初级的训练中，设计两个例题，分别是针对矩阵乘法不满足交换律和消去律的探讨，从而将其不满足的性质从特殊推广到一般。

两个例题让学生分组完成，在表象结果的基础上，引导学生思考矩阵乘法不满足的性质，并深刻的分析其原因，使学生的认知发生质的飞跃。

2.3 类比的思想

矩阵乘法的性质，通过类比实数乘法的性质，平行得出结果，充分体现了旧知类比得出新知的理念。具体有

3 从实践的角度设计应用

线性代数来源于生活实际，又很好地服务于科学研究和生活，所以在导入环节（情境创设）通过大量的图片介绍其广泛的应用。在升华环节，通过具体的实例分析其详细的应用。通过表象感触和深入探讨的结合，使学生深刻领悟到矩阵乘法的广泛应用。

（1）导入环节：首先从矩阵乘法在图片加密，字体变换，人脸识别，搜索引擎，图像处理，我国自主研发的飞机设计中的应用案例，进行课题导入。紧接着通过如何快速计算工厂的总收入和总利润问题，归纳、总结、抽象矩阵乘法的法则。

（2）应用环节：通过设计，明文—加密—密文，展示了矩阵乘法的应用，同时也为，密文—解密—明文，中逆矩阵的学习埋下伏笔。

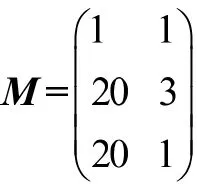
4 从课程思政的角度设计

课程思政贯穿于本节课的始终，从多角度和多维度进行融入，有爱国情怀，数学史、数学文化以及数学家的精神，攻坚克难的勇气，团队协作精神和精益求精精神等。

4.1 爱国情怀

情境创设、课题引入环节，设计了运20和歼20的总设计师——西北工业大学最牛上下铺——杨伟与唐长红，感悟他们为了国之重器奉献终生的精神。

4.2 数学史、数学文化以及数学家的精神方面

一是科学家的执着精神。介绍了英国数学家凯莱的成长成才经历，在被迫放弃自己热爱的工作时，也没有间断自己为之着迷的数学研究。

二是团队合作的力量。凯莱与他的金牌搭档英国数学家西尔维斯特，一起为了代数型不变理论的研究的奋斗历程。

三是奉献精神。积极主动投身社会工作，为了剑桥大学接收女性学生发挥了很大的作用，借此引出“七一勋章”获得者，“全国优秀共产党员”张桂梅老师。

4.3 攻坚克难的勇气

设计了三个逐步递进的环节，梯度式的上升，在实践中锤炼学生求真的意志和能力，攻坚克难的勇气。

第一阶段：基础初级阶段—简单的矩阵乘法法则的练习；

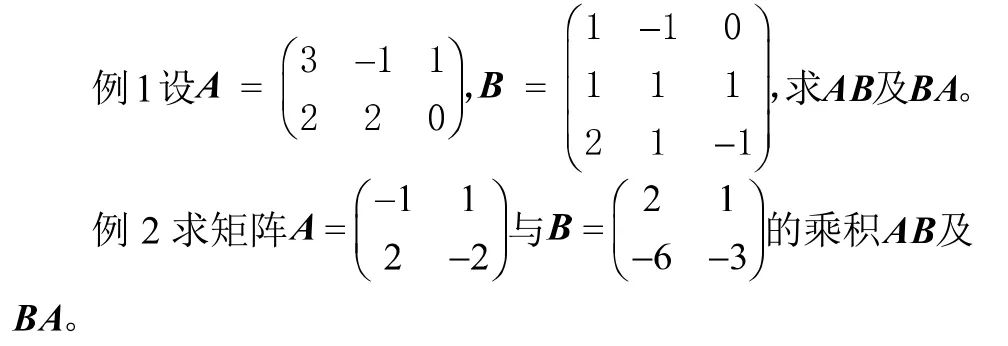
第二阶段：提高、应用—重走长征路，体会凯莱发明矩阵乘法的初衷，深刻感受科学家的求真精神，以及矩阵乘法的广泛应用。

例3已知两个线性变换

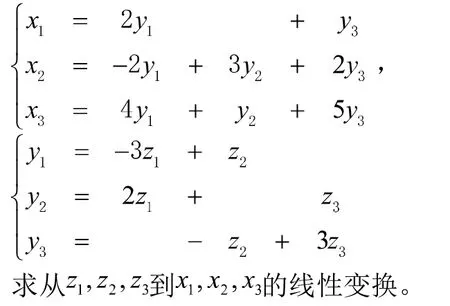
第三阶段：延伸、拓展—巧妙利用矩阵乘法的结合律，解决矩阵幂的计算问题。

4.4 通过合作式学习，培养学生的团队协作精神和精益求精精神

团队协作精神和精益求精精神贯穿整个教学设计的始终。小组合作探究环节，两人一组，在团队成员之间可以对探究结果反复补充，直到满意为止。

5 学生中心

“以学生为中心”的理念，是整个教学设计的出发点、落脚点、产出点，也是灵魂之所在。

（1）两次学习通3分钟测试（课前、课后）。

（2）学生小组合作（两两一组），希沃白板学生作品展示，让学生时时处处、真真切切参与课堂。在充分体现“学生中心”的基础上，教师随时随刻掌握学生的学习情况。

（3）通过PPT、希沃白板、黑板、学习通的无缝切换，让智慧课堂淋漓尽致的展现，从而显著提高学生课堂参与度和课堂的时效性。

6 总结

本文研究了工程数学——线性代数的教学设计问题，基于教材、学情、教学目标、教学重难点，从理论、实践、课程思政、学生中心四个角度，通过问题驱动和案例式的方法，秉承学生中心的理念，进行了教学设计的深层次探讨和实践。