基于双重中位数绝对偏差的证据加权组合方法
2022-12-17吴根秀蔡奥丽
余 鑫,吴根秀,蔡奥丽
(江西师范大学数学与统计学院,江西 南昌 330022)
0 引言
证据理论是20世纪60年代末至70年代初由A.P. Dempster[1]提出的,并由他的学生G. Shafer[2]进一步修改并发展,因此也称该理论为D-S证据理论.D-S证据理论在证据合成中是迄今为止使用最频繁的一种证据融合规则,被广泛地应用于信息融合、神经网络、故障诊断等领域[3-9].由于证据会受到不确定性因素的影响,所以当证据融合时往往也会得到不确定性的结果.D-S合成规则需要解决的核心问题是:在面对高度冲突的证据融合时会产生不符合直觉的结果,如L.A. Zadeh[10]提出的悖论、“一票否决”问题等.基于此,近几十年来,国内外许多学者针对D-S证据理论在进行证据融合时产生的问题提出了许多改进的方法.这些方法主要分为2类.一类是修改D-S证据理论的合成规则.此类方法认为D-S本身存在一定的局限性,在面对高度冲突的证据融合时没有做到合理地分配而产生了有悖直觉的结果;其中有R.R. Yager[11]的合成规则、孙全等[12]的合成规则、吴根秀[13]的合成规则等.R.R. Yager的合成规则是直接将冲突的信息分配给识别框架,这种方法认为冲突是由客观的无知造成的.R.R. Yager的合成规则虽然解决了在证据完全冲突时的D-S合成规则无法合成的问题,但高度冲突证据的加入会导致合成结果难以识别目标和无法做出相应的决策.孙全等的合成规则是引入了可信度来度量证据之间的可信程度,并认为证据之间存在冲突部分也是可用的,然而该方法的合成效率不高.吴根秀的合成规则是在引入自冲突概念的基础上提出了一种权重分配算法,最后通过算例计算得到了较好的融合结果.另一类是修改原始证据源.这种方法认为高度冲突证据是受到不确定因素的干扰导致的,因此在证据融合之前需要将证据预处理,即修改原始的证据源;其中有C.K. Murphy[14]的合成规则、邓勇等[15]的合成规则.C.K. Murphy的合成规则是先将原始证据的基本概率分配(BPA)函数值取算术平均修改成新的证据值,然后再将修改后的证据值进行D-S合成,该方法没有充分考虑不同证据之间的影响与联系.邓勇等的合成规则是为了考虑证据之间的联系,引入一个度量证据与证据之间的距离的Jousseleme函数[16],并进一步获得证据之间的相似度和由其他证据产生的各个证据的支持度,最后将证据进行加权后再利用D-S合成规则进行证据融合.该方法虽然改进了C.K. Murphy的合成规则的不足,但是忽略了证据自身的影响.
以上几种方法在一定程度上都是对经典D-S证据理论合成规则做出的改进,但对证据融合效率有待提高.基于此,本文提出了一种既考虑证据源对融合的影响,又考虑D-S合成规则自身缺陷的新合成方法.该方法首先认为证据融合效果不好是证据源本身的问题(即存在异常证据),在证据融合之前需要先对异常证据进行修改,认为冲突较高的证据是受到某些不确定的因素影响导致的;然后通过引入双重中位数绝对偏差(MAD)检测出异常证据,将异常证据使用平均值法进行修正;最后将修改的证据进行新的加权组合得到最终结果.
1 预备知识
1.1 基础知识
定义1设Θ={θ1,θ2,…,θn}为一个有限识别框架,映射m:2Θ→[0,1]满足
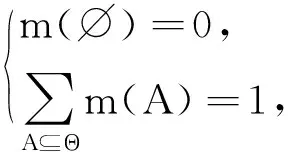
则称m为Θ上的基本概率分配(basic probability assignment,BPA)函数,简称BPA函数.称m(A)为A的基本概率分配;∀A⊆Θ,m(A)表示对A的支持度,若m(A)>0,则称A为m的焦元.所有焦元的集合构成基本概率分配的核(core),记为C(m).
1.2 D-S合成规则及其存在的问题
为了将n个独立信息源的证据进行融合,Dempster-Shafer提出一种合成规则,其本质是将这些证据进行直交和计算.D-S合成规则如下:设m1,m2,…,mn为幂集2Θ上的n个基本概率分配函数,则D-S合成公式为
(1)
(2)

在经典的D-S合成规则中,当在2条证据融合后K值为1时,这2条证据完全冲突,此时D-S合成规则就失效了;当K→1时,该2条证据之间高度冲突,此时在进行证据的融合后将会产生与直觉不符的结果,例1和例2说明了这种情况.
1.2.1 Zadeh悖论问题
例1识别框架Θ={a,b,c},2条证据m1和m2对该识别框架的各个目标基本概率分配分别为
m1:m1(a)=0.99,m1(b)=0.01,m1(c)=0;
m2:m2(a)=0,m2(b)=0.01,m2(c)=0.99.
由式(1)~(2)计算得K=0.999 9,m(a)=m(c)=0,m(b)=1.虽然这2条证据对目标b的基本概率分配值都很低,但是在进行D-S合成后却对目标b的基本概率分配值为1,完全肯定了目标b,此结果显然是有悖直觉的,这个问题最早是由L.A. Zadeh[10]提出的,称之为Zadeh悖论.
1.2.2 一票否决问题
例2识别框架Θ={a,b,c},2条证据m1和m2对该识别框架的各个目标基本概率分配分别为
m1:m1(a)=0.8,m1(b)=0.1,m1(c)=0.1;
m2:m2(a)=0,m2(b)=0.2,m2(c)=0.8;
m3:m3(a)=0.7,m3(b)=0.2,m3(c)=0.1.
由式(1)~(2)计算得K=0.988 0,m(a)=0,m(b)=0.33,m(c)=0.67.从合成结果来看,虽然很多证据对目标a的支持度都较高,但是只要出现1条证据的m(a)=0,合成的结果就是m(a)=0,即对目标a始终持否定态度,出现了一种“一票否决”的现象.
1.3 已有的几种解决冲突证据合成规则的修正方法
1.3.1 R.R. Yager的合成规则 R.R. Yager[11]认为冲突的信息是无用的信息,基于此提出了对D-S合成规则的改进,改进公式为
其中Θ为其他的未知命题,K为冲突因子.该方法的最大的优势是解决了D-S合成规则可能带来的悖论.当冲突因子K不是很大时,该方法合成的效果具有一定的价值;不过该方法同样也存在一定的问题,当冲突因子K接近于1时,冲突的部分会分配给未知命题,从而导致焦元获得的概率很小而无法做出最终的决策.当证据较多时,也可能产生“一票否决”现象.
1.3.2 C.K. Murphy的合成规则 C.K. Murphy[14]则在平均信度优先情况下提出了一种对证据冲突进行合理简便处理的改进方法,改进公式为
mM(A)=(m1(A)+m2(A)+…+mn(A))/n,∀A⊆Θ.
1.3.3 孙全等的合成规则 孙全等[12]进一步改进了R.R. Yager[11]的方法,改进公式为

孙全等[12]提出了一种加权求和的方法,同时引入证据之间可信度的概念,将冲突的证据根据可信度分成2类,该方法提升了融合结果的可靠性.然而该方法在需要快速识别并做出决策的领域中应用的效果是有待提高的.
1.3.4 邓勇等的合成规则 邓勇等[15]的合成规则是在C.K. Murphy的合成规则基础上考虑证据之间的联系,引入了一个度量证据与证据之间的距离的Jousseleme函数[16],并通过计算得到证据之间的支持度s(mi),然后通过归一化处理得到证据mi的可信度r(mi),并将它作为证据mi的权重,最后在对证据进行加权平均后再利用D-S合成规则进行证据的融合,其改进部分的公式为
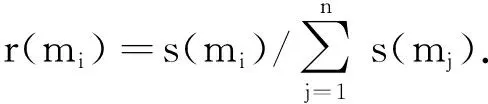
1.3.5 刘康等的合成规则 刘康等[17]认为数据的融合不仅要遵循算法的客观规则,而且要考虑决策者的主观判断.基于此,提出一种基于本征向量和Jousseleme距离[18]的权重分配方法,该方法有效地提高了高度冲突证据融合的准确度和可靠性.
2 基于双重中位数绝对偏差(MAD)的证据加权方法
2.1 基于MAD的异常证据检测方法
2.1.1 基本概念 双重中位数绝对偏差被简称为MAD[19],该统计方法近几年来在异常值检测领域[20]中备受青睐.下面定义了这一方法的基本概念.
设有一列数据:x1,x2,…,xn,Md(xj)(j=1,2,…,n)为这列数据的中位数,用M表示,其表达式为
M=Md(xj)(j=1,2,…,n).
(3)
MAD算法是在中位数基础上发展而来的[21-22],称Mσ为双重中位数绝对偏差值,其表达式为
Mσ=Md(|xj-M|)(j=1,2,…,n).
(4)
为了对数据中的异常值进行检测,给出判定范围S,其表达式为
S=[M-εMσ,M+εMσ],
(5)

2.1.2 基于MAD的异常证据检测方法 本文将MAD在数理统计中对数据检测的方法引入证据推理中.下面首先给出异常焦元和异常证据的定义.
定义2设Θ={θ1,θ2,…,θn}为有限识别框架,m1,m2,…,mn为Θ上的基本概率分配函数,若∀Aj⊆Θ,有mi(Aj)>0且mi(Aj)∉S(i=1,2,…,n),则称Aj为证据mi的异常焦元(abnormal focal element).
定义3设Θ={θ1,θ2,…,θn}为有限识别框架,m1,m2,…,mn为Θ上的基本概率分配函数,若存在异常焦元Aj⊆Θ,且Aj∈C(mi)(i=1,2,…,n),则称证据mi为异常证据(abnormal evidence).即若在1条证据中存在异常焦元,则该证据一定是异常证据.
2.1.3 随机模拟实验检测该方法的有效性 为了检测该方法的有效性,下面做3组随机模拟实验.
根据式(3)~(5)可以计算出图1~图3在5条证据融合时的各个焦元的正常范围(见表1).从随机产生的数据和通过式(3)~(5)计算出来的S,BPA值不属于S的证据被认定为异常证据也是比较符合直觉的.下面给出检测异常证据的一般步骤与3个具体的实例.

图1 随机产生第1组5条证据的BPA值
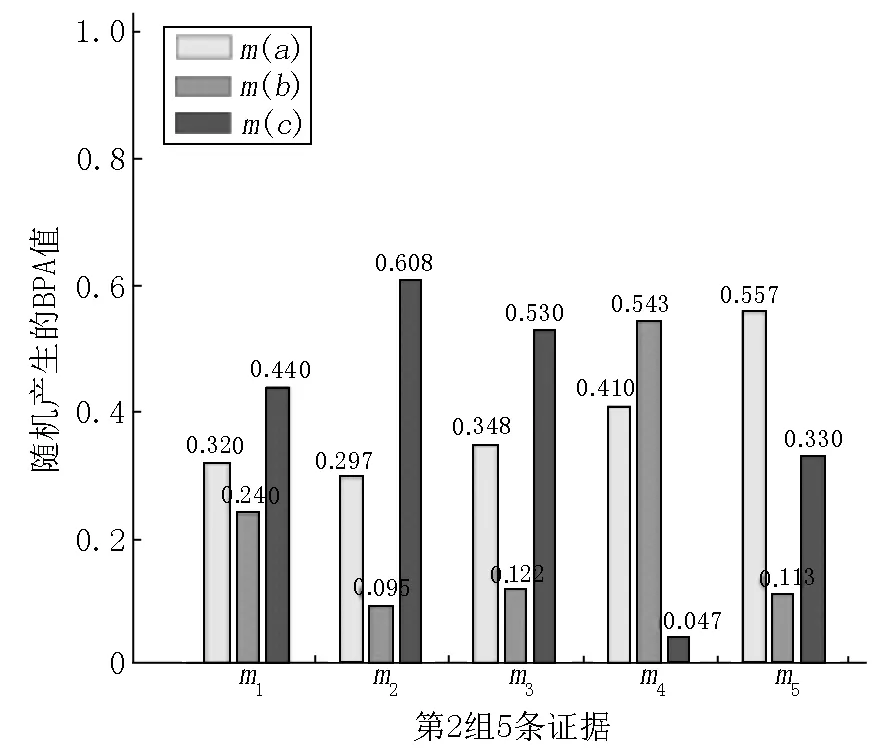
图2 随机产生第2组5条证据的BPA值
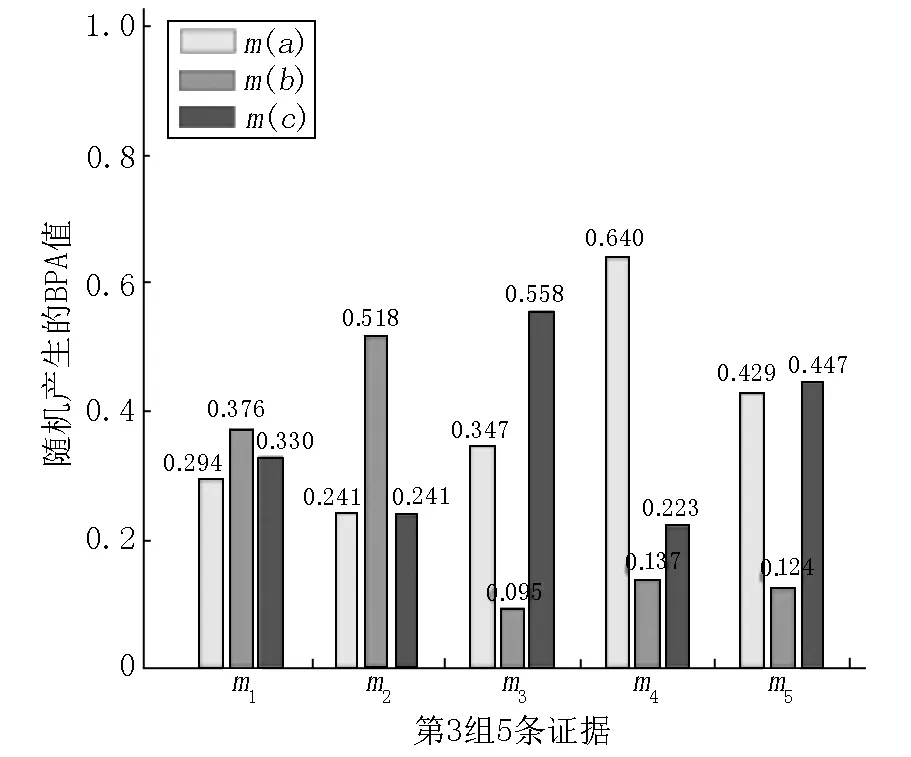
图3 随机产生第3组5条证据的BPA值
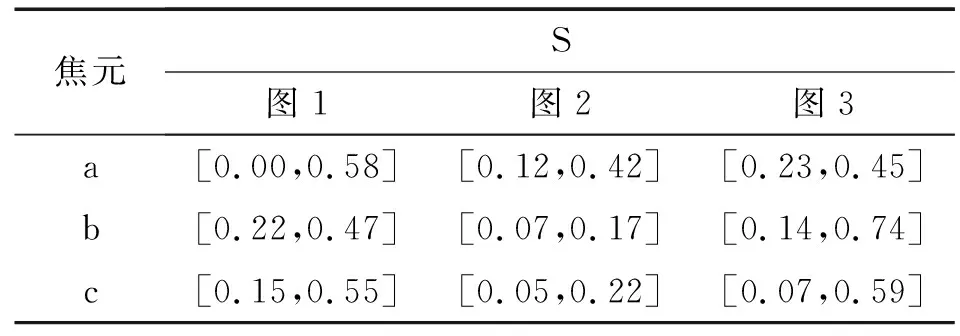
表1 在5条证据融合时各个焦元的正常范围
2.1.4 检测异常证据的一般步骤
Step 1通过式(3)~(4)可以计算出每个焦元的双重中位数绝对偏差Mσ(m(Aj))(j=1,2,…,l),其中Mσ(m(Aj))表示在n个证据源中同一焦元的Mσ值.
Step 2通过式(5)计算出焦元Aj的判定范围S(Aj)(j=1,2,…,l).
Step 3判断各个焦元是不是异常焦元.若mi(Aj)∈S(Aj)(i=1,2,…,n),则Aj为证据mi的正常焦元;若mi(Aj)∉S(Aj)(i=1,2,…,n),则Aj为证据mi的异常焦元.
Step 4判断各个证据是不是异常证据.若∃Aj⊆Θ,使得mi(Aj)∉S(Aj)(i=1,2,…,n)且Aj∈C(mi)(i=1,2,…,n),则称证据mi为异常证据;若∀Aj⊆Θ,使得mi(Aj)∈S(Aj)(i=1,2,…,n)且Aj∈C(mi)(i=1,2,…,n),则称证据mi为正常证据.
在证据源的检测中,对于含有异常焦元的异常证据,MAD算法对证据源的数量并不敏感,即使在较少的证据源(n≥3)中也依然可行,且该算法检测出的异常证据是符合直觉的.下面通过3个例子检测的数据说明这个算法的合理性.
例3设在1个盒子中装有1个球,已知球的颜色为绿色、红色、黄色之一,令a、b、c分别表示红色、黄色、绿色,则可以给出它的识别框架为Θ={a,b,c},有2条证据m1和m2对Θ的各个目标的基本概率分配为
m1:m1(a)=0.2,m1(b)=0,m1(c)=0.8;
m2:m2(a)=0.8,m2(b)=0,m2(c)=0.2.
通过MAD算法检测异常焦元.表2给出了在m1、m22条证据合成时各个焦元的正常范围.

表2 在m1、m2证据合成时各个焦元的正常范围
例4在例3的基础上加1条证据m3,其对各个目标的基本概率分配为
m3:m3(a)=0.2,m3(b)=0,m3(c)=0.8.
通过MAD算法检测异常焦元,在m1、m22条证据合成时各个焦元的正常范围与例3一样.表3给出了在m1、m2、m33条证据合成时各个焦元的正常范围.

表3 在m1、m2、m3证据合成时各个焦元的正常范围
例5在例4的基础上加1条证据m4,其对各个目标的基本概率分配为
m4:m4(a)=0.4,m4(b)=0,m4(c)=0.6.
通过MAD算法检测异常焦元,在m1、m2、m33条证据合成时各个焦元的正常范围与例4一样.表4给出了在m1、m2、m3、m44条证据合成时各个焦元的正常范围.

表4 在m1、m2、m3、m4证据合成时各个焦元的正常范围
从上述3个例子可知:MAD算法检测的焦元的正常范围会随着证据的加入而发生改变,具有自适应性.通过本文给出的算法可以得出:当证据源n≤2时,无法检测出异常证据.这是因为在仅有1条或2条证据时证据的各个焦元的基本概率分配值一定在正常范围内.
该算法当n≥3时就可以检测出异常证据,即该方法更适用于证据数量多的情形,而这些检测出来的异常证据与人们的直觉相符.
2.2 基于MAD检测证据加权组合的新方法
如前所述,D-S合成规则被广泛地应用于证据的融合,且具有一些良好的性质,然而在面对高度冲突的证据源时该方法对数据的融合会产生一些悖论.为了避免这种现象发生,C.K. Murphy[14]通过提出一种证据的算术平均方法来对证据进行预处理,此方法在一定程度上改进了D-S合成规则面对高度冲突证据的不足,但此方法没有充分考虑各个证据之间的联系.为了解决这个问题,邓勇等[15]提出了基于Jousselme距离的证据加权平均的方法,该方法继承了C.K. Murphy方法的所有优点,并且考虑了证据之间的联系,在一定程度上有较好的合成效果,但该方法忽略了证据本身对数据的影响.本文基于这3种方法提出了一个新的证据加权组合方法.
本文方法的核心思想是:将收集到的多源证据通过MAD算法检测是否存在异常证据,若不存在异常证据则就直接使用证据加权组合方法得出最终的合成结果;若含有异常证据,则先将异常证据用这组证据的平均值证据进行修正,再将修改后的证据使用D-S合成规则、C.K. Murphy的合成规则、邓勇等的合成规则3种方法进行加权组合,其改进公式为
m(A)=β1m1(A)+β2m2(A)+β3m3(A),
(6)

(7)
其中mk、ml为证据的向量形式,D为2N×2N矩阵,矩阵D中的元素dij=|Ai∩Aj|/|Ai∪Aj|,∀Ai,Aj⊆Θ,N为Θ中元素的个数.2条证据的距离越大说明这2条证据之间的相关性程度越小,故本文在αi≠0(i=1,2,3)时使用
1/αi(i=1,2,3)
(8)
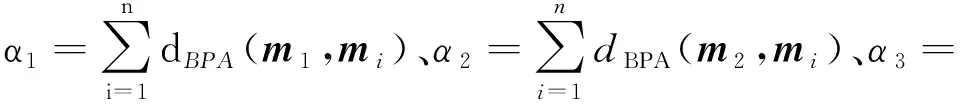

βi=(1/αi)/(1/α1+1/α2+1/α3)(i=1,2,3,αi≠0),
(9)
这样就确定了权重分配的系数,从而可以通过式(6)计算出最终的结果.为了验证该方法的有效性,下面通过随机模拟实验和仿真实验来说明本文方法可以较好地解决证据源高度冲突融合问题.
2.3 本文方法流程图
图4为基于MAD检测的证据加权组合方法流程图.
2.4 对本文算法时间复杂度进行分析
2.4.1 对本文的检测算法进行分析 本文通过MAD算法计算出Mσ和S.1)先将对同一焦元的赋值大小进行排序,其次数为n2;2)进行1次取中位数操作,共进行n次.后面的步骤的执行次数均不超过O(n2).故该算法的时间复杂度为O(n2).
2.4.2 对本文加权组合新方法进行分析 本文需要通过Jousselme距离函数计算出α1、α2、α3的值.1)先计算出其他3种合成方法的结果;2)计算出权重α1、α2、α3的值.前2步算法的时间复杂度为O(n2).后面的步骤的执行次数均不超过O(n2).故该算法的时间复杂度为O(n2).
2.5 随机模拟实验检测本文合成方法的有效性
为了检测本文合成方法的是否比已有的方法有效,本文用合成后的最终结果与原始证据之间的Jousselme距离d来评价本文方法的优劣.合成结果的评价标准为:d越小说明合成结果与原始证据越接近,即该方法合成结果变形程度越小,合成的效果越好;d越大说明合成结果与原始证据越远,即该方法合成结果变形程度越大,合成的效果越差.现使用Matlab随机模拟100次,每次随机生成100条基本概率分配函数,计算出合成结果与原始证据之间的距离并绘制出图5.
从图5可知:本文方法计算出的结果与原始证据之间的距离较小,这说明本文方法计算的最终结果变形程度小,合成的效果较好.其他3种方法计算出来的结果与原始证据之间的距离较大,特别是经典的D-S合成规则计算出的最终结果变形程度较大且不稳定.这也解释了近几十年来许多学者[23-24]对经典的D-S合成规则要改进的原因.
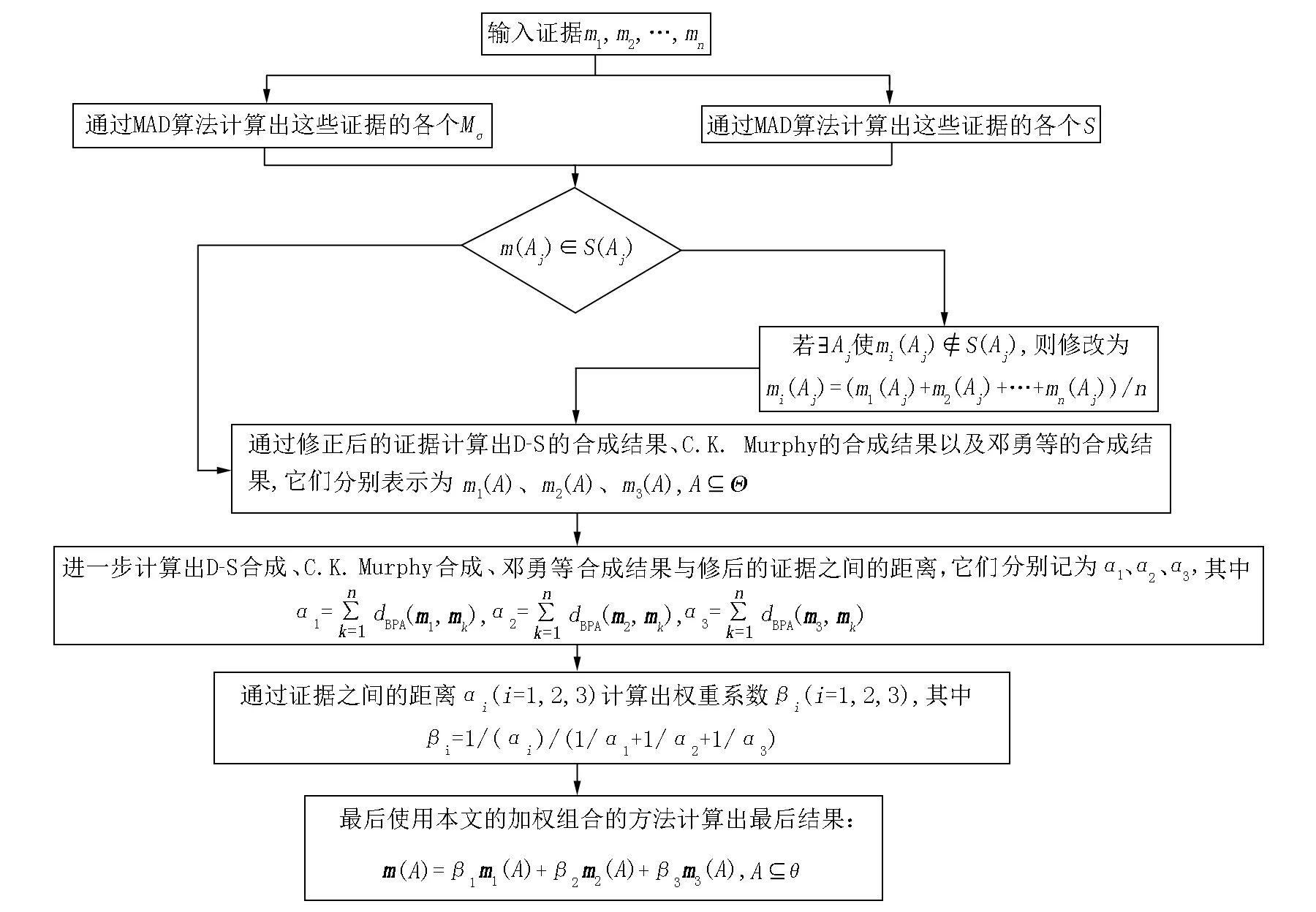
图4 本文方法流程图
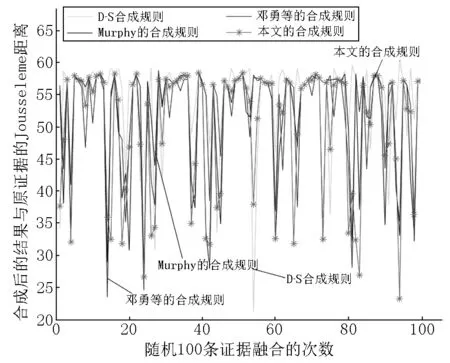
图5 随机模拟实验图
2.6 使用本文方法对例1、例2进行分析
对例1使用本文的加权组合方法进行证据的合成.由于本文的MAD算法无法检测出只有2条证据的异常证据,所以本文的检测方法对例1是失效的,故直接使用本文提出的基于Jousselme距离的证据权重组合方法进行数据的融合.通过式(7)~(9)可以计算出β1=0.193 4,β2=0.403 3,β3=0.403 3;然后通过式(6)可以计算出m(a)=0.40,m(b)=0.20,m(c)=0.40,其结果与D-S合成规则、C.K. Murphy的合成规则、邓勇等的合成规则的融合结果进行比较(见表5).

表5 例1的4种合成规则结果比较
从表5中的数据可以得出:经典的D-S合成规则在面对冲突性数据融合时产生与直觉不符的结果,而C.K. Murphy的合成规则、邓勇等的合成规则的融合结果对目标a与目标c的支持度均为0.5,对目标b持否定态度,存在一定的缺陷.从本文的合成规则结果来看,该方法对这3种方法都考虑了,得到的结果没有绝对地否定目标b,对目标a和目标c的支持度都是一样的(各占0.4),这比较合理.
对例2使用本文的加权组合方法进行证据的合成.由于在使用本文的MAD算法时,当只有2条证据m1、m2时无法检测出异常证据,所以计算方法与例1的一样,最终融合结果与D-S合成规则、C.K. Murphy的合成规则、邓勇等的合成规则的融合结果进行比较(见表6).当加入第3条证据m3时,通过MAD算法检测异常焦元,表7为在m1、m2、m33条证据合成时各个焦元的正常范围.

表6 例2的4种合成规则结果比较

表7 在m1、m2、m33条证据合成时各个焦元的正常范围
由表7中的焦元a的正常范围可知证据m2需要修改,由焦元b的正常范围可知证据m1需要修改,故将证据m1、m2使用这组证据的平均值进行修正,修改后的结果为
m′1:m′1(a)=0.50,m′1(b)=0.17,m′1(c)=0.33;
m′2:m′2(a)=0.50,m′2(b)=0.17,m′2(c)=0.33;
m′3=m3:m3(a)=0.70,m3(b)=0.20,m3(c)=0.10.
将修改后的证据使用本文提出的基于Jousselme距离的证据权重组合方法进行数据的融合.通过式(7)~(9)可以计算出β1=0.347 8,β2=0.332 4,β3=0.319 8.再使用本文的证据权重组合方法与证据修正后的D-S合成规则、C.K. Murphy的合成规则、邓勇等的合成规则的融合结果进行比较(见表8).
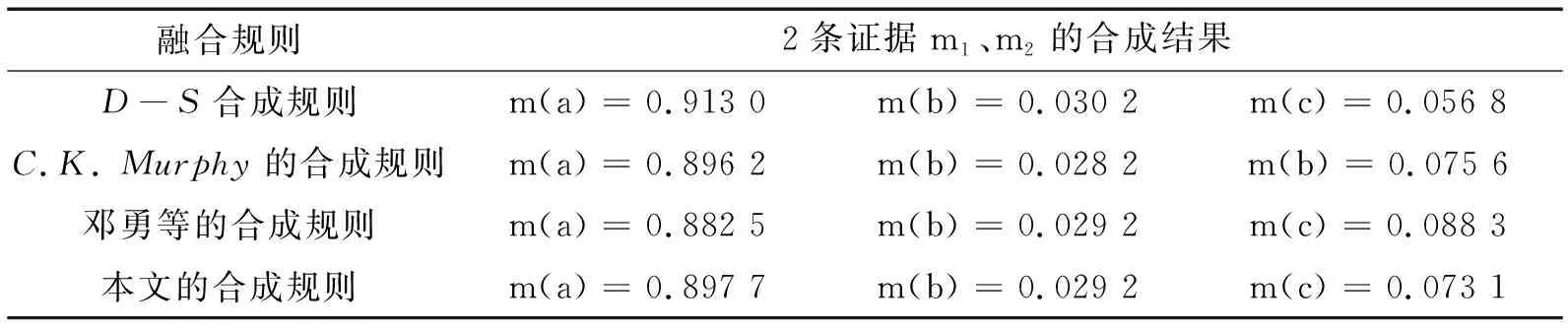
表8 例2的修正后4种合成规则结果比较
从表8的数据可以得出:在使用本文的MAD算法检测出异常证据并修正后,再使用D-S合成规则、C.K. Murphy的合成规则、邓勇等的合成规则、本文的合成规则进行融合,得到的结果均比较合理,这说明本文的MAD算法是有效的.由于在2.5节的随机模拟实验中考虑合成结果的稳健性,所以使用本文的加权组合方法来对修正后的证据源进行合成.从合成结果来看,本文方法可以较好地解决Zadeh悖论问题与“一票否决”问题.
下面通过具体仿真实验来说明本文方法在面对高度冲突证据的融合时也能够快速高效地做出决策.
3 仿真实验
为了验证本文加权组合的新方法的效果,本文将采用文献[17]的完整算例进行仿真实验来验证本文算法的有效性.
例6设有3个目标的识别框架:Θ={A,B,C},收集的5条证据对目标A、B、C的基本概率分配值如图6所示.
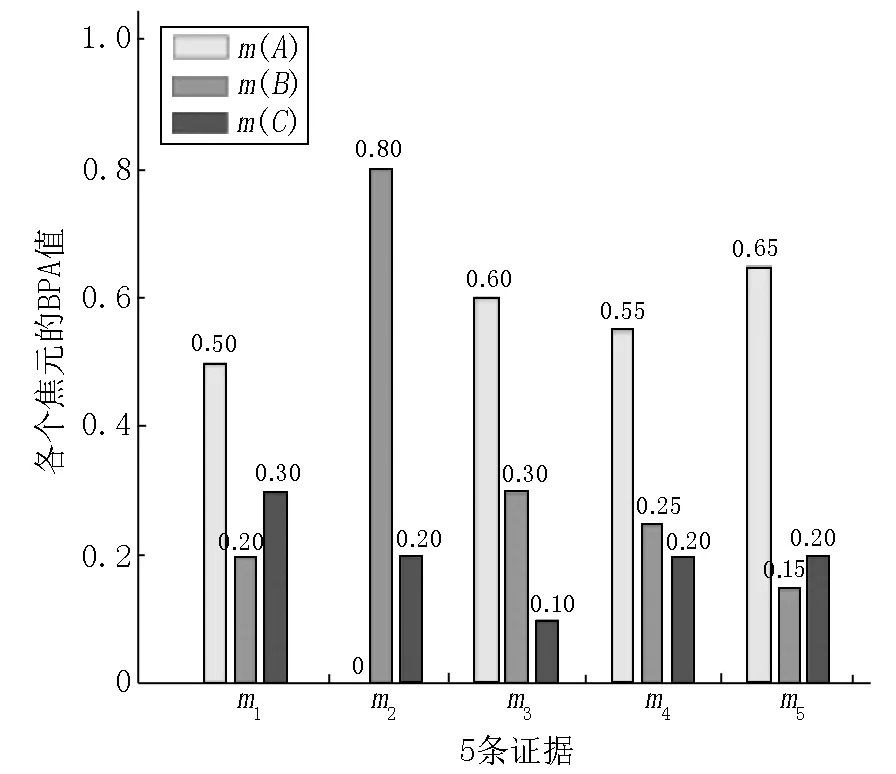
图6 5条证据对目标A、B、C的BPA值
从这5条证据来看,m1、m3、m4、m5都认为目标A的可能性较大,而证据m2却否定了目标A,根据直觉可以认为证据m2的情况应该是因受到某些不确定因素影响而导致的.根据本文的合成规则,首先通过MAD算法找出异常焦元,然后对含有异常焦元的异常证据进行修改,最后在对修改的证据进行证据的加权平均后使用D-S合成规则融合.表9是在证据m3、m4、m5逐步加入后各个焦元的正常范围.
从表9中各个焦元的正常范围可以得到:当证据m1、m2融合时,无法检测出异常证据;当加入证据m3时,由各个焦元的正常范围可知证据m2需要修改;当再加入证据m4时,从表9中数据可知证据m2需要修改;当5条证据都进行融合时,由各个焦元的正常范围可知证据m1、m2、m3需要修改.将修正后的证据使用本文的合成方法进行合成并与7种合成规则做比较(为了更好地体现本文方法的有效性,文献[25]的合成方法的结果也列于表中),其结果如表10所示.
由表10的数据可得8种合成规则对A、B、C支持度随着融合证据的加入的变化趋势(见图7~图9).

表9 各焦元的正常范围
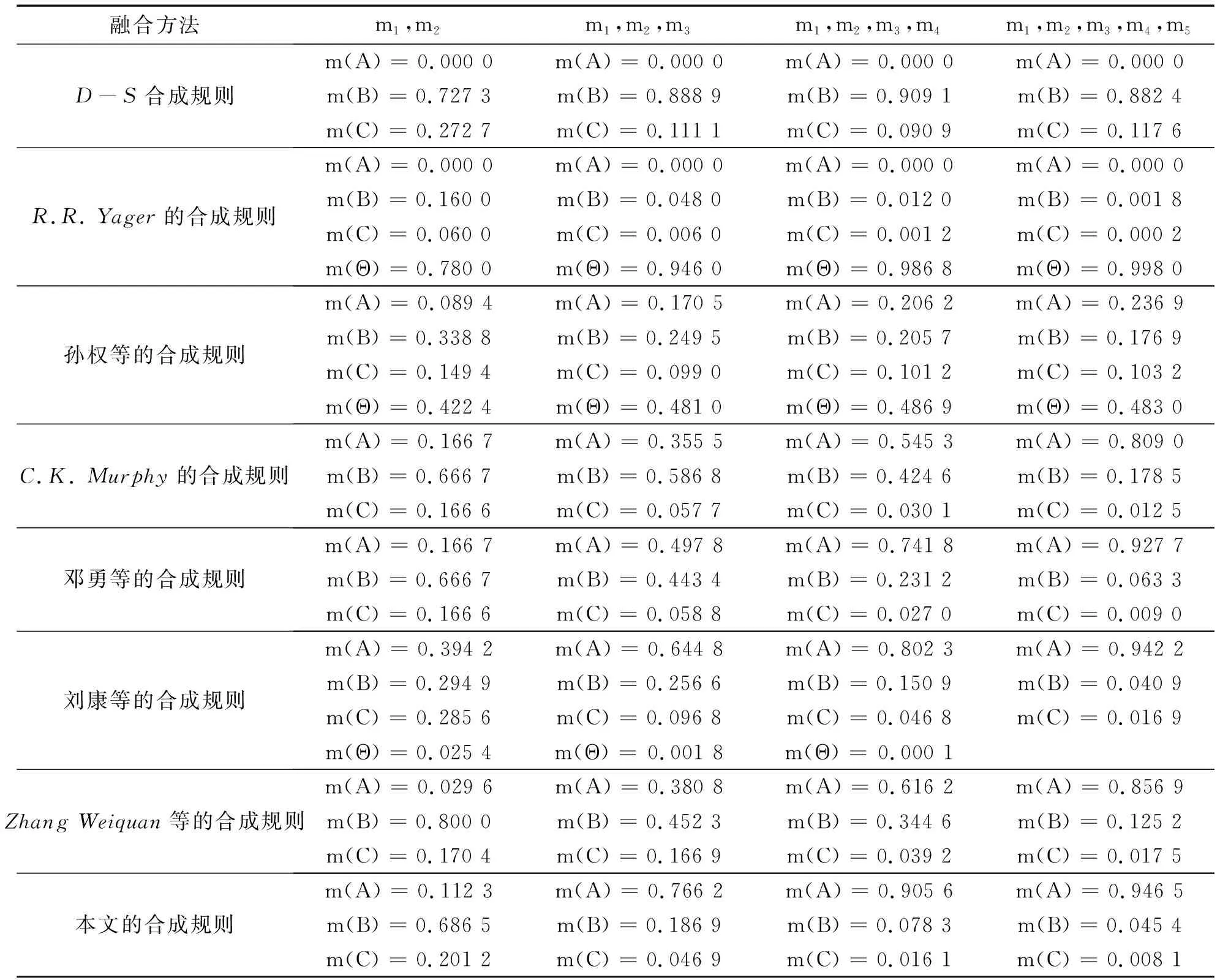
表10 8种合成规则结果比较
根据表10和图7信息可以看出:对于D-S合成规则,尽管在5个证据源中有4个证据源都支持目标A,但是由于冲突证据m2(A)=0,所以融合的结果m(A)始终是0,出现了“一票否决”的结果,这明显是不合理的结果.在面对高度冲突的证据时,R.R. Yager、孙权等的合成规则是将大部分支持度赋值给未知Θ,这也一样没有得到合理的融合结果.当只有3条证据时,C.K. Murphy的合成规则、邓勇等的合成规则并不能较好地做出决策,这是因为这2种方法对目标A与B的支持度都接近0.5;只有刘康等的合成规则与本文的合成规则对目标A的支持度均高于0.6且对其他目标的支持度都很低,并且本文的合成规则对目标A的支持度高达 0.905 6.随着更多的证据源进行融合,本文的合成规则对目标A的支持度越来越合理,当有5条证据源融合时,本文的合成规则对目标A的支持度高达0.946 5.

图7 8种合成规则对目标A的BPA值
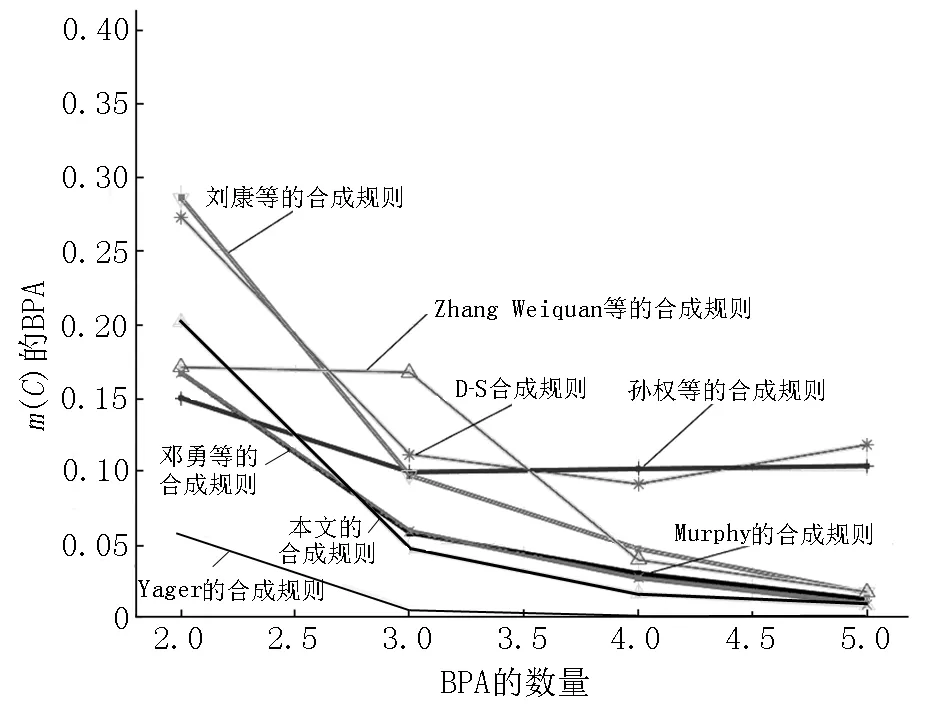
图9 8种合成规则对目标C的BPA值
本文的合成规则是建立在文献[1,14-15]的基础上的,它的过程是:先将接收到的信息源进行预处理,再通过MAD算法检测出异常证据源,最后将异常证据源用这组证据的平均值进行修正后通过证据加权组合得到最终结果.
由图7可以看出:本文的合成规则可以较快地对目标A做出决策;然而当只有2条证据源进行融合时,该方法无法检测出异常证据;随着证据的加入,对错误目标B、C的支持度能较快地下降.与其他方法比较,本文方法可以快速高效地做出决策.
4 结束语
针对经典的D-S合成规则在面对较高冲突证据融合时会产生有悖常理的结果,本文提出了一种基于双重中位数绝对偏差的检测方法和证据加权组合修正方法,该检测方法是在数理统计中经常使用的对数据异常值检测的方法,本文将其对在证据理论中的异常证据进行检测,从算例的数据可以得出该检测方法有效.仿真实验数据表明:本文改进的方法对证据融合具有较快的收敛性,比在实验中的其他8种方法效果更好,这在一定程度上解决了证据源的高度冲突融合问题.
在对未来的研究工作中,笔者将重点研究合理分配算法的证据权重、提高算法的计算效率、降低算法的时间复杂度等.
