求解对流扩散方程的4阶紧致差分格式

李冉冉,王红玉,开依沙尔·热合曼

(新疆大学数学与系统科学学院,新疆 乌鲁木齐 830046)

0 引言

对流扩散方程是在偏微分方程中一个重要的分支，被用于描述排水膜中的传热、溶解物质的分散、液体溶质的扩散等现象，被广泛应用于环境科学，流体力学等众多领域中.本文研究1维对流扩散方程的初边值问题:

(1)

其中α为扩散系数,β为对流系数,f、g1、g2均为已知充分光滑的函数,u为待求未知量.

近年来，求解该问题的数值方法有有限差分法[1-10]、有限元法[11]和有限体积法[12]等.由于有限差分法十分简便且有效，因此在求解该问题时得到很多研究者的青睐.文献[3]用梯形方法构造该问题的时间2阶、空间4阶精度的差分格式.文献[4]对该问题应用时间3阶、空间2阶精度的差分格式，该格式在数值模拟上取得较好的结果，但在空间方向上的精度有待提高.针对这种情况，学者们对空间变量提出高阶紧致差分格式，文献[5]给出关于1阶、2阶导数4阶紧致离散格式并应用于两点边值问题的数值计算.文献[6-7]将文献[5]中4阶紧致格式应用于Kuramoto-Sivashinsky和耦合Burgers方程组的数值模拟中.文献[8]对定常对流扩散反应方程提出4阶精度的差分格式，并通过结合Richardson技术达到提高计算精度的目的.文献[9]通过结合紧致差分格式和4阶边值法构造出时间空间同时具有4阶精度的格式.文献[10]利用3次Hermite插值公式来求解双曲型电信方程，在时间方向上取得4阶精度.通过以上分析，本文将结合文献[5]和文献[10]的方法，对带有周期和Dirichlet边界条件的对流扩散方程构造时间空间同时具有4阶精度的绝对稳定的差分格式.

本文给出了空间离散格式以及描述了时间离散算法，并对格式的稳定性给出了证明和满足2种边界条件下的算例的数值验证.

1 空间离散

1.1 在周期边界条件下对流扩散方程的差分格式

考虑具有周期边界的对流扩散方程:

(2)

为了逼近在对流扩散方程中的空间导数，将计算域Ω×[0,T]={(x,t)|0≤x≤L,0≤t≤T}划分为由点集{(xj,ti)}描述的均匀网格，记xj=jΔx,j=0,1,…,N,Δx=L/N,ti=iΔt,i=0,1,…,M,Δt=T/M,称Δx和Δt分别为空间步长和时间步长.

本文的空间变量的1阶导数项和2阶导数项使用4阶紧致差分公式[5]

u′j-1+4u′j+u′j+1=3(uj+1-uj-1)/Δx,j=1,2,…,N

(3)

来近似,其中u′j表示u(x)在j处1阶导数的近似值.

式(3)写成矩阵形式:

L1U′=M1U,

U=(u1,u2,…,uN)T,U′=(u′1,u′2,…,u′N)T.

则空间变量的1阶导数可以表示为

(4)

若u″j表示u(x)在j处的2阶导数的近似值,则有

u″j-1+10u″j+u″j+1=12(uj-1-2uj+uj+1)/Δx2,j=1,2,…,N.

(5)

式(5)写成矩阵形式:

L2U″=M2U,

U″=(u″1,u″2,…,u″N)T.

则空间变量的2阶导数可以表示为

(6)

将式(4)和(6)代入方程(2)得到常微分方程

dU/dt=A1U,

(7)

1.2 在Dirichlet边界条件下对流扩散方程的差分格式

为了逼近在对流扩散方程中的空间导数，将计算域Ω×[0,T]={(x,t)|a≤x≤b,0≤t≤T}划分为由点集{(xi,tj)}描述的均匀网格，记xj=a+(j-1)Δx,j=1,2,…,N,Δx=(b-a)/(N-1),ti=iΔt,i=0,1,…,M,Δt=T/M.

本文的空间变量的1阶和2阶导数同样用上述4阶紧致格式[5]来近似,空间变量的1阶导数项用

4u′2+u′3=(-11u1/12-4u2+6u3-4u4/3+u5/4)/Δx,j=1,

u′j-1+4u′j+u′j+1=3(uj+1-uj-1)/Δx,j=2,3,…,N-1,

u′N-2+4u′N-1=(-uN-4/4+4uN-3/3-6uN-2+4uN-1+11uN/12)/Δx,j=N

(8)

来逼近.式(8)写成矩阵形式:

LxU′=MxU+b1,

Mx=

b1=11(-u1,0,…,0,uN)T/(12Δx),

U=(u2,u3,…,uN-1)T,

U′=(u′2,u′3,…,u′N-1)T.

则空间变量的1阶导数可以表示为

(9)

空间变量的2阶导数用

14u″2-5u″3+4u″4-u″5=12(u1-2u2+u3)/Δx2,

j=1,

u″j-1+10u″j+u″j+1=12(uj-1-2uj+uj+1)/Δx2,j=2,3,…,N-1,

(10)

来逼近.式(10)写成矩阵形式:

LxxU″=MxxU+b2,

其中

Lxx=

Mxx=

b2=12(u1,0,…,0,uN)T/Δx2,

U″=(u″2,u″3,…,u″N-1)T.

则空间变量的2阶导数可以表示为

(11)

将式(9)和(11)代入方程(1)得常微分方程

dU/dt=A2U+B1b2-C1b1,

图1为1/4波长换能器和变幅杆模型，1为前盖板，2为压电陶瓷堆，3为后盖板，4、5为阶梯型变幅杆。由于超声加工属于轻负载场合，在设计夹心式超声振子时，可以忽略负载对共振频率的影响，按照空载进行计算。当系统共振时，存在某处振动位移为零的节点。该节点所在平面称为波节面，将波节面AB设计在换能器前盖板上，截面将超声换能器分为两部分，根据一维传输线理论可以分别求得这两部分的频率方程[9]：

(12)

2 3次Hermite插值法

3次Hermite插值多项式p(x)[10]可以写成

p(x)=f(x0)h0(x)+f(x1)h1(x)+f′(x0)·H0(x)+f′(x1)H1(x),

(13)

其中

h0(x)=(1+2(x-x0)/(x1-x0))((x-x1)/

(x0-x1))2,

h1(x)=(1+2(x-x0)/(x0-x1))((x-x0)/

(x1-x0))2,

H0(x)=(x-x0)((x-x1)/(x0-x1))2,

H1(x)=(x-x1)((x-x0)/(x1-x0))2.

在如下定理中，给出了3次Hermite插值多项式(13)的误差.

定理1[13]设有2个不同的点x0、x1,且f∈C4[x0,x1].若p(x)是3次Hermite插值多项式，则在区间[x0,x1]中的每个x都对应于[x0,x1]中的1个点ξ，有

f(x)-p(x)=f(4)(ξ)(x-x0)2(x-x1)2/24.

(14)

根据等式(14)和定理1可以得到积分公式

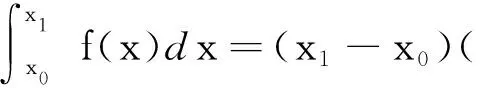
(15)

在周期边界下，常微分方程(7)应用3次Hermite插值(15),有

因此,式(2)的差分格式为

(16)

同理，常微分方程(12)应用3次Hermite插值(15),则在Dirichlet边界下的对流扩散方程(1)的差分格式为

(17)

其中b′1=11(-∂u1/∂t,0,…,0,∂uN-2/∂t)T/(12Δx),b′2=12(∂u1/∂t,0,…,0,∂uN-2/∂t)T/(Δx)2.

3 稳定性分析

引理1[14]设G=(gij)n×n为严格对角占优的，则

1)G是可逆的;

2)若G的所有主对角线项都为正，则G的所有特征值都有正实部;

3)若G是Hermite矩阵,且G的所有主对角线项都为正,则G的所有特征值都为正实数.

引理2[15]若z的实部是非正的，则

|(12+6z+z2)/(12-6z+z2)|≤1.

定理2本文差分格式(16)和(17)的截断误差为o(Δt4+Δx4)且无条件稳定.

λj=αλll/λmm-βλl/λm.

|(λE)j|≤1(j=1,2,…,n+1).

在本文格式(17)的齐次情况下，结构与格式(16)是一致的，因此，格式(16)、(17)都是无条件稳定的.因为紧致离散格式(4)、(6)、(9)、(11)在空间方向上为4阶，且3次Hermite插值公式在时间方向上为4阶，因此差分格式(16)、(17)截断误差为o((Δt)4+(Δx)4).

4 数值实验

为了研究本文格式的可靠性，对满足2种边界条件下的算例进行数值计算，并比较了本文格式的L2范数误差及空间时间的收敛阶.表1～表4给出了：本文格式(16)、(17)的时间变量均为Crank-Nicolson，空间变量分别为中心差分格式[1]o((Δx)2+(Δt)2)、4阶差分格式[2](HOC)

o((Δx)4+(Δt)2).其中L2范数误差和收敛阶的定义分别为

r=lg(‖u-UΔx(Δt)‖/‖u-UΔx(Δt)/2‖/lg 2,

其中Uk、uk分别表示点xk处的数值解和准确解.

例1考虑具有周期边界的对流扩散方程[16]:

其准确解为u(x,t)=e-αtsin(x-βt),其中α=β=1,L=2π.

表1和表2针对周期边界的对流扩散方程,当T=1、Δt=0.002和T=1、Δx=1/60时,给出了在不同Δx和Δt的L2范数误差和收敛阶的比较.由表1和表2可以看出:当空间变量离散分别为2阶中心差分格式、HOC,时间变量离散为Crank-Nicolson时,本文格式(16)具有更小的误差,且在时间和空间方向上都达到了4阶精度,这与理论结果相符合.

例2考虑具有Dirichlet边界的对流扩散方程[17]:

表1 例1中当T=1、Δt=0.002、不同Δx时的L2范数误差和收敛阶比较

表2 例1中当T=1、Δx=1/60、不同Δt时的L2误差和收敛阶比较

表3和表4针对Dirichlet边界的对流扩散方程,当T=1、Δt=(Δx)2和T=1、Δx=0.012 5时,给出了在不同Δx和Δt时的L2范数误差和收敛阶的比较.由表3和表4可以看出:当空间变量离散分别为2阶中心差分格式、HOC,时间变量离散为Crank-Nicolson时,本文格式(17)具有更小的误差,且在时间和空间方向上都达到了4阶精度,这与理论结果相符合.

表3 例2中当T=1、Δt=(Δx)2、不同Δx时的L2范数误差和收敛阶比较

表4 例2中当T=1、Δx=0.012 5、不同Δt时的L2误差和收敛阶比较

5 结论

本文在周期和Dirichlet边界条件下对空间变量的离散达到了4阶精度，并结合3次Hermite插值法提出了数值求解1维对流扩散方程在空间和时间上都具有4阶精度且绝对稳定的差分格式.采用本文的方法计算了2个数值算例，从表1和表3可知:本文的格式在空间上达到了4阶的精度，与传统的中心差分格式和HOC格式相比，体现了本文格式的有效性；从表2和表4可知:本文的格式在时间上也达到了4阶的精度，与Crank-Nicolson相比，本文的格式更精确.另外，该格式也可以通过利用局部1维化方法推广到2维和3维对流扩散方程问题的数值计算中.