建筑因素对环境温度的显著影响分析

卢跃静，武新乾，王飞飞

（河南科技大学，河南 洛阳 471023）

引文

随着我国经济的迅速发展，建筑业已成为我国国民经济的重要支柱产业[1]。近年来，一些学者对建筑因素对环境温度的影响进行了研究。耿红凯等（2020）指出样地温度与绿量（含三维绿量、乔木覆盖率、绿化覆盖率等指标）存在负相关关系[2]；孙喆（2020）提出城市形态要素对热环境具有显著影响，建筑密度上升导致地表温度上升，容积率、绿地率的提升引起地表温度下降[3]；王琳（2017）指出中庭式建筑中庭各层温度的特点是沿高度方向，高度越高，温度越高[4]。

本文主要就建筑因素绿化率、密度和高度对环境温度的影响进行显著性分析。

1 数据来源与数据处理

1.1 数据来源

数据来源：河南科技大学建筑学院实地测量数据，包括建筑因素绿化率、密度、高度及其对应环境温度440组数据；建筑因素绿化率、密度、高度与环境温度散点图见图1-图3。

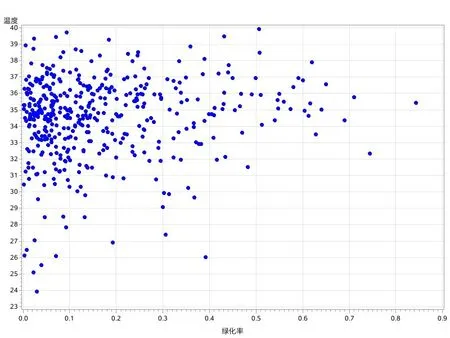
图1 温度与绿化率散点图

图2 温度与密度散点图

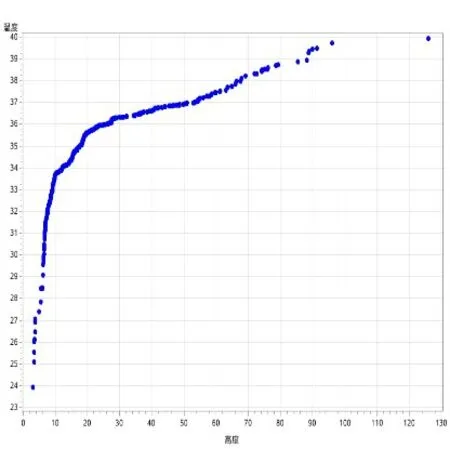
图3 温度与高度散点图

2.2 数据处理

数据处理：对绿化率、密度、高度数据进行Min-max标准化，即：

其中yi为xi标准化的值。

2 建筑因素对环境温度的影响

将绿化率、密度、高度分为11个水平，每组40个数据进行单因素方差分析[5]。

对不同绿化率水平下的温度进行正态性检验，结果见表1。由表1可知，绿化率水平1、水平2、水平4、水平7 对应温度不服从正态分布，则不能对绿化率进行单因素方差分析[6]。

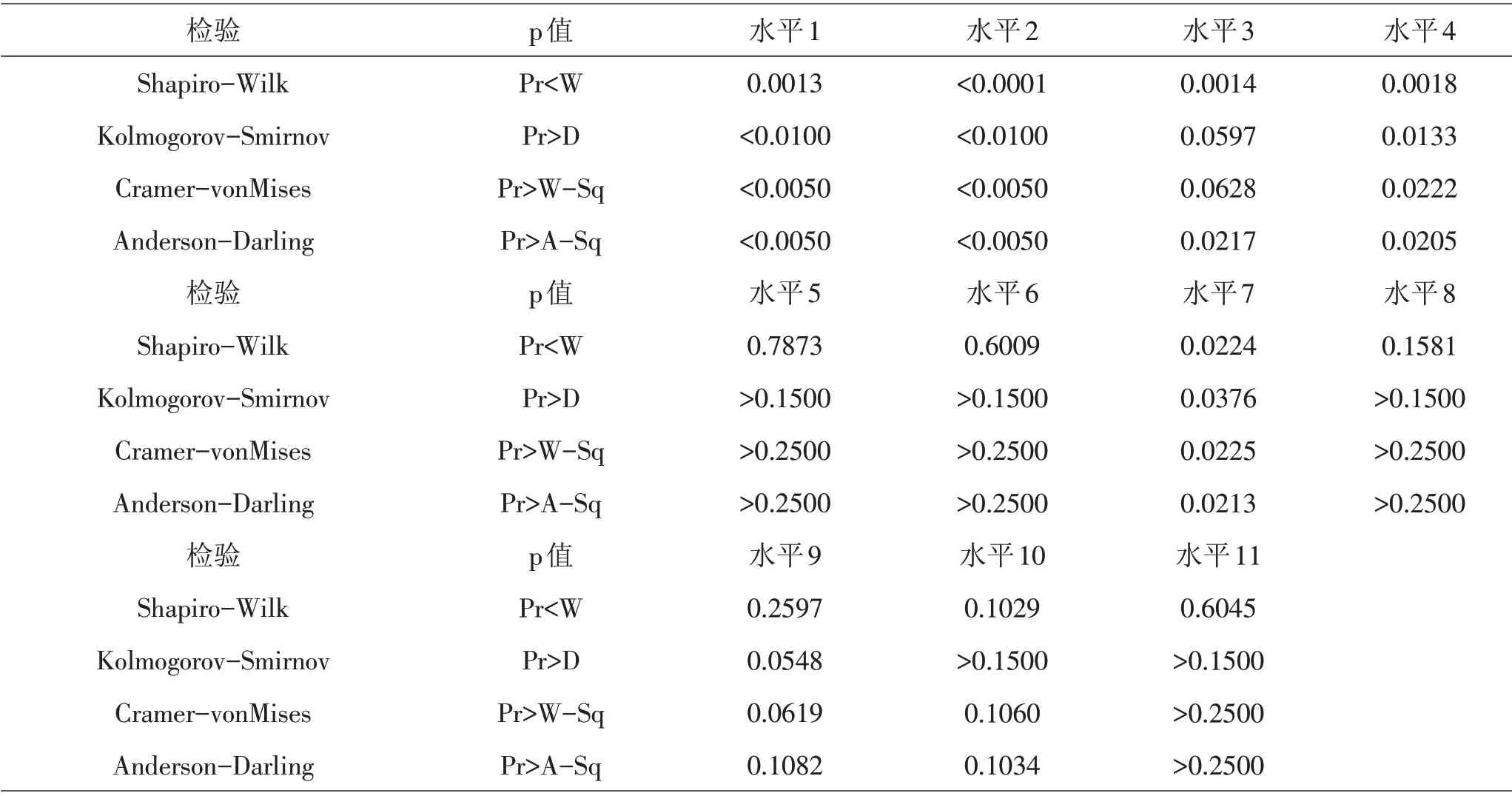
表1 不同绿化率水平下的温度正态性检验

对不同密度水平下的温度进行正态性检验，结果见表2。由表2可知，密度水平4、水平8、水平11对应温度不服从正态分布，从而不能对密度进行单因素方差分析[6]。

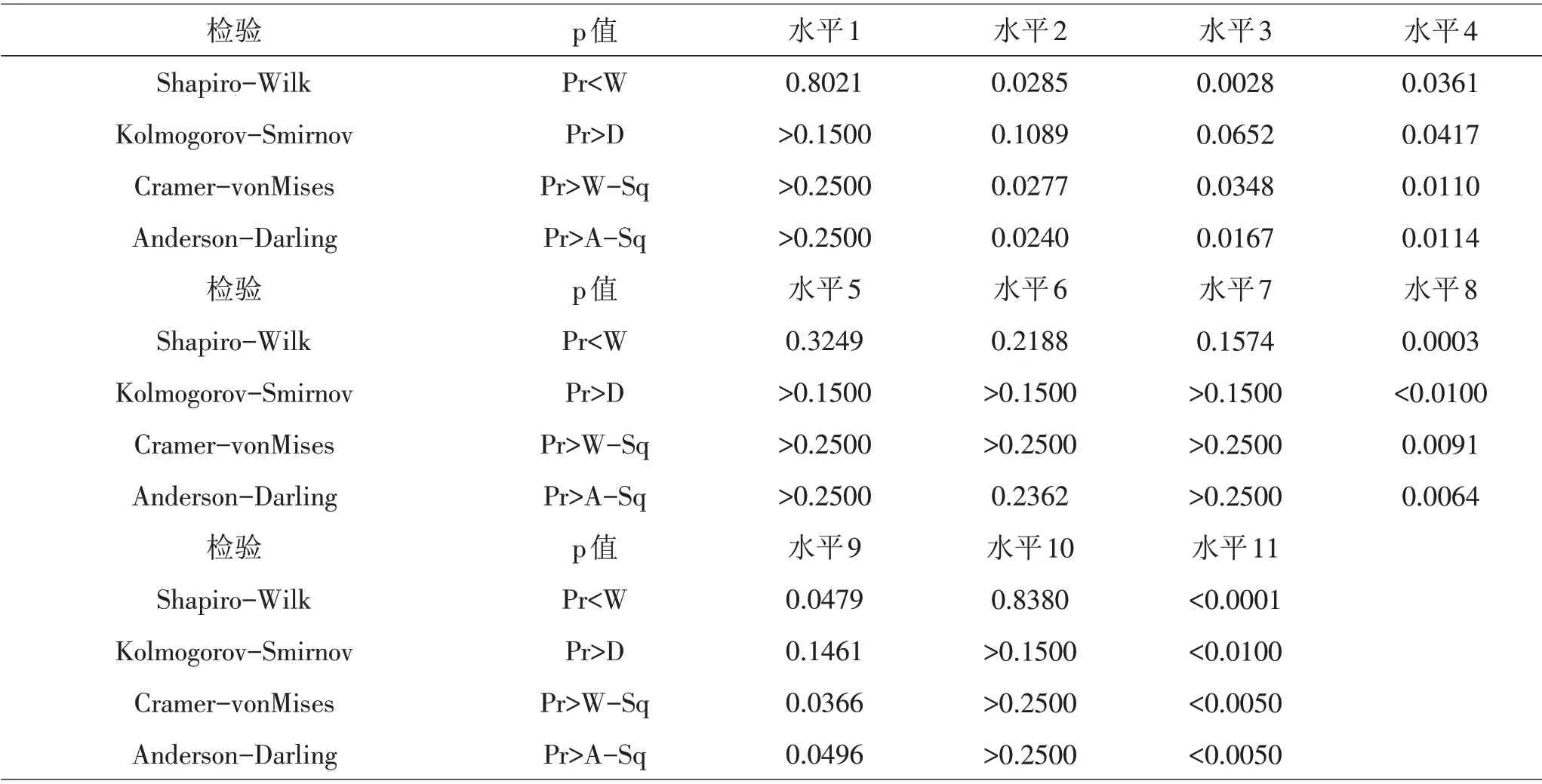
表2 不同密度水平下的温度正态性检验

对不同高度水平下的温度进行正态性检验，结果见表3。由表3可知，高度水平1、水平3、水平9 对应温度不服从正态分布，不能对高度进行单因素方差分析[6]。

表3 不同高度水平下的温度正态性检验

对于建筑因素绿化率、密度、高度，均存在水平对应温度不服从正态分布，故不能直接对该组数据进行方差分析，且考虑到在探究建筑因素对温度的影响时没有进行变量控制，于是进行K-means 聚类[7]以达到控制变量的目的，从而更好地探究建筑因素对温度的影响。

2.1 建筑因素绿化率对环境温度的影响

利用建筑因素密度、高度标准化后数据，用手肘法画出肘部图，见图4。由图4，曲线在K=4 时，曲率最大，则最佳类聚数量值K 值取4。利用R软件进行K-means 聚类[7]，聚类结果见图5。

图4 密度、高度聚类肘部图

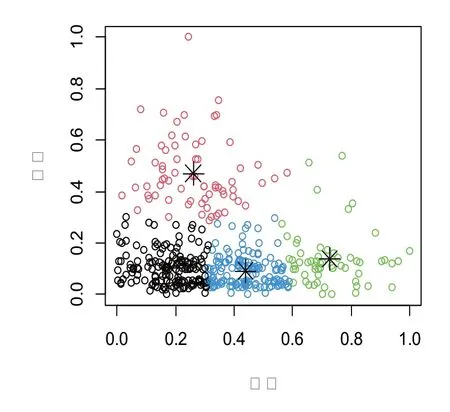
图5 密度、高度聚类结果图

根据密度、高度标准化数据进行K-means聚类，将样本分为4类，数据个数分别为203、154、34、49。选取数据个数为203的类别进行处理，绿化率因素下的8个分类变量分别是0～0.1、0.1～0.2、0.2～0.3、0.3～0.4、0.4～0.5、0.5～0.6、0.6～0.7以及0.7以上总称为绿化率因素下的八个水平[8]。对每个绿化率水平下的温度进行正态性检验，结果见表4。由表4可知，绿化率水平1、水平2、水平4、水平5下的温度数据不服从正态分布；此外，进行Levene方差齐性检验，结果见表5。由表5可知，p值＜0.05，方差非齐。故不能采用单因素方差分析方法探究绿化率对环境温度的影响[6]。

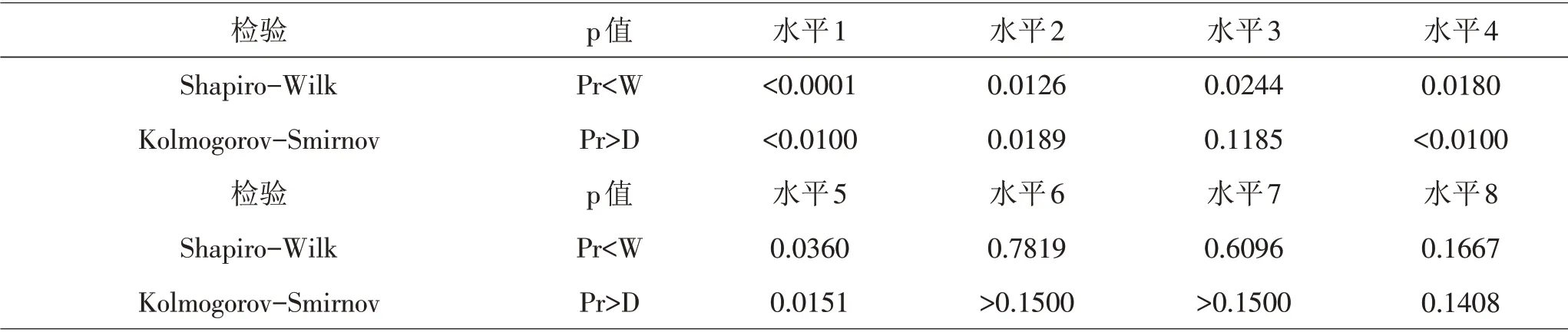
表4 不同绿化率水平下温度数据的正态检验结果

表5 Levene方差齐性检验

考虑采用非参数检验方法Kruskal-Wallis方法[9]进行检验。对数据进行Kruskal-Wallis检验，结果[10]见表6。由表6可知，p值＜0.05，拒绝原假设，即认为建筑因素绿化率对环境温度有显著影响。

表6 Kruskal-Wallis检验结果

2.2 建筑因素密度对环境温度的影响

将数据进行标准化，利用建筑因素绿化率、高度标准化数据画出肘部图，见图6。由图6可知，曲线在K=3 时，曲率最大，由此确定最佳类聚数量值K 值为3，即将原始数据聚为3类。利用R 软件进行K-means 聚类[7]，聚类结果见图7。

图6 绿化率、高度聚类肘部图

图7 绿化率、高度聚类结果图

根据绿化率、高度标准化数据进行Kmeans 聚类，将样本分为3类，数据个数分别为91、287、62。选取数据个数为287 的类别进行处理，密度因素下的9 个分类变量分别是0～0.1、0.1～0.2、0.2～0.3、0.3～0.4、0.4～0.5、0.5～0.6、0.6～0.7、0.7～0.8 以及0.8～0.9 总称为密度因素下的九个水平[8]。对每个密度水平下的温度进行正态性检验，结果见表7。由表7可知，密度水平2、水平4、水平5、水平7、水平9 下的温度数据不服从正态分布；此外，进行Levene 方差齐性检验，结果见表8。由表8可知，p 值＞0.05，不能拒绝原假设，即认为方差齐性。但由于存在密度水平对应温度正态性检验未通过，故不能采用单因素方差分析方法探究密度对环境温度的影响[6]。

表7 不同密度水平下温度数据的正态检验结果

表8 Levene方差齐性检验结果

故采用Kruskal-Wallis 检验[9]探究建筑因素密度对环境温度的影响。检验结果见表9。由Kruskal-Wallis 检验结果[10]，p 值＞0.05，不能拒绝原假设，即认为建筑因素密度对环境温度无显著影响。

表9 Kruskal-Wallis检验结果

2.3 建筑因素高度对环境温度的影响

将数据进行标准化，利用建筑因素绿化率、密度标准化数据画出肘部图，见图8。由图8可知，曲线在K=5 时，此时误差平方和SSE 的下降趋于缓慢，由此确定最佳类聚数量值K 值为5，即将原数据分为5类。利用R 软件进行K-means 聚类[7]，聚类结果见图9。

图8 绿化率、密度聚类肘部图

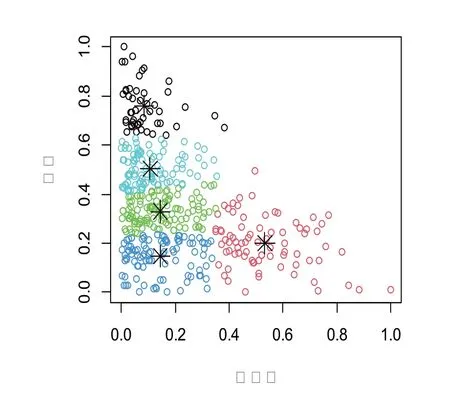
图9 绿化率、密度聚类结果图

根据绿化率、密度标准化数据进行Kmeans 聚类，将样本分为5类，数据个数分别为127、66、69、116、62。选取数据个数为127的类别进行处理，高度因素下的7 个分类变量分别是0～10、10～20、20～30、30～40、40～50、50～60、以及60 以上总称为高度因素下的七个水平[8]。对每个高度水平下的温度进行正态性检验，结果见表10。由表10可知，高度水平1下的温度数据不服从正态分布；此外，进行Levene 方差齐性检验，结果见表11。由表11可知，p 值＞0.05，不能拒绝原假设，即认为方差齐性。但由于存在高度水平对应温度正态性检验未通过，故不能采用单因素方差分析方法探究高度对环境温度的影响[6]。

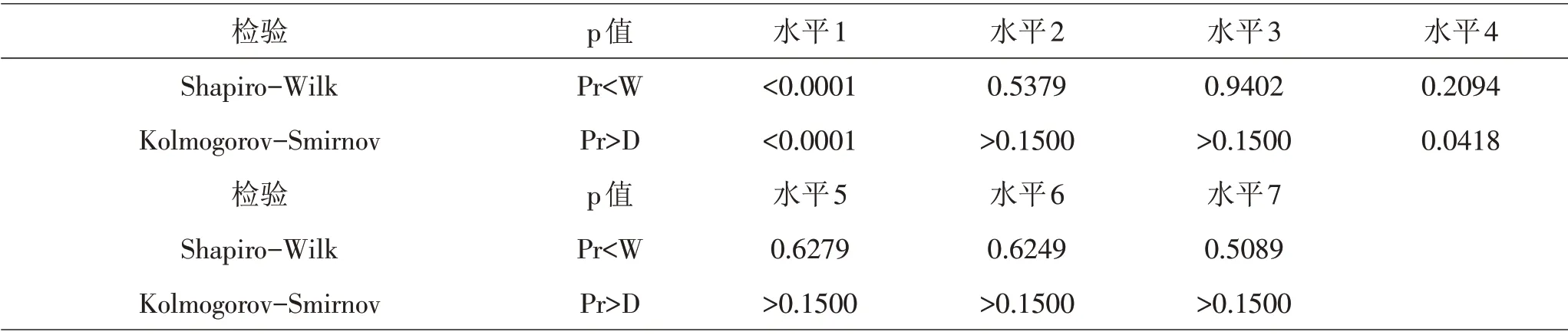
表10 不同高度水平下温度数据的正态检验结果

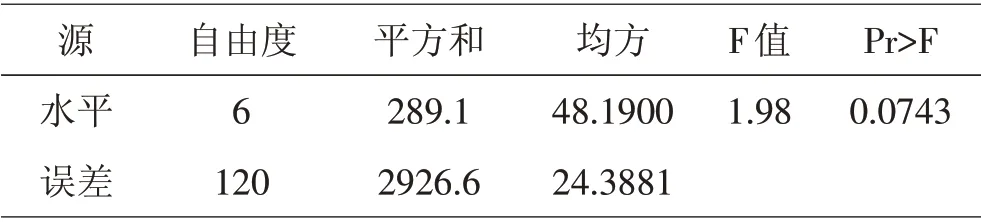
表11 Levene方差齐性检验结果

考虑采用非参数检验方法Kruskal-Wallis方法[9]探究建筑因素高度对环境温度的影响。检验结果见表12。由Kruskal-Wallis 检验结果[10]，p 值＜0.05，拒绝原假设，即认为建筑因素高度对环境温度有显著影响。

表12 Kruskal-Wallis检验结果

3 结语

本文就三个建筑因素对环境温度的显著影响进行了探究，通过K-means动态聚类控制变量，具体检验了数据是否满足单因素方差分析的条件，运用非参数检验得出建筑因素绿化率、高度对环境温度有显著影响，建筑因素密度对环境温度的影响不显著的结论。因此，可通过改变建筑因素绿化率、高度以减弱热岛效应，提高环境质量，推进绿色建筑发展。