四旋翼无人机在线规避航迹规划方法

赵文娇，甘旭升

(1 山西工程科技职业大学交通工程学院，山西 晋中 030619；2 空军工程大学空管领航学院，西安 710051)

0 引言

随着神舟十二号载人航天顺利着陆、神舟十三号载人航天成功发射，各型四旋翼无人机频频出境，在载人航天搜救回收任务中发挥了重要作用，已成为当前执行搜救回收任务的主要承载方式。四旋翼无人机相对传统无人机而言，有着垂直升降、机动性强和操作方便等多方面的优点，这使得四旋翼无人机在航天发射与回收、军事侦察、警方搜索、火灾救援、农情监测以及影视拍摄等诸多领域发挥重要作用[1-4]。

航迹规划在实现四旋翼无人机机动高效和安全飞行中发挥着重要作用，它是根据当前地形环境为四旋翼无人机规划出满足若干任务要求的一条由起点到终点的最优或次优航行路径，是当前四旋翼无人机领域的重要研究方向[5-6]。相关的航迹规划研究也吸引了大量学者，例如文献[7]针对四旋翼无人机低空飞行实时规避需求，构建目标和威胁的虚拟力场，提出了一种基于人工势场的二维航迹规划方法，使得无人机沿着边缘规避障碍。文献[8]针对无人机航迹规划通常假设环境静态且需要地形先验知识的现状，提出了一种实时局部航迹重规划方法(real-time trajectory, RTT)，以更有效地应对未知、动态的障碍物。文献[9]基于经典Teach-and-Repeat框架，提出了一种完整、鲁棒的四旋翼无人机航迹自主规划方法(teach repeat replan，TRR)，具有全局规划和局部感知的综合性能，进一步改善了航迹规划在全局误差、定位漂移和动态规避等方面问题。文献[10]为进一步准确获取无人机未来时刻位置，采取限制角速度的方式对航迹规划模型进行改进，从而提出了一种基于卷积神经网络的无人作战飞机飞行轨迹预测算法，以提高无人机机动决策的预见性。文献[11]针对无人机航迹规划高运算率、高执行性需求，改进ARA*三维航迹规划模型，提出了一种无人飞行器在线航路筹划方法，进一步适应动态规划与时间最优性的综合要求。

城市高楼林立、山区地形起伏、深林植被茂密，很难达到固定翼飞机的起降标准，而四旋翼无人机以其垂直起降、空中悬停等优势具有更强的适应能力。四旋翼无人机为了适应不同的、复杂未知的环境，避免飞行过程中与障碍物发生碰撞，必须具备在线规避和航迹重规划能力[5，12]。目前，多数无人机仍采用地面远程操控或跟踪规划的方式来进行航迹规划，所使用的航迹规划方法多数是在飞行环境完全已知，且飞行过程中环境条件不变的情况下，飞行器按照事先规划好的航迹飞行[7，13-14]。此外，四旋翼无人机是一个多输入、欠驱动、强耦合的非线性系统，飞行时沿空间直角坐标系3个方向位移运动并绕坐标系3轴旋转运动，但仅有4个可控电机转速输入变量控制，一般的航迹算法在精度上可能有所不足[15-17]。

针对上述问题，提出一种面向未知复杂环境的四旋翼无人机在线规避航迹规划方法，采用分段多项式对四旋翼无人机飞行航迹进行建模，在保证系统安全性的前提下优化规避航迹，在C++环境中搭建仿真模型并验证方法可行性。

1 四旋翼无人机空间运动模型

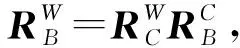
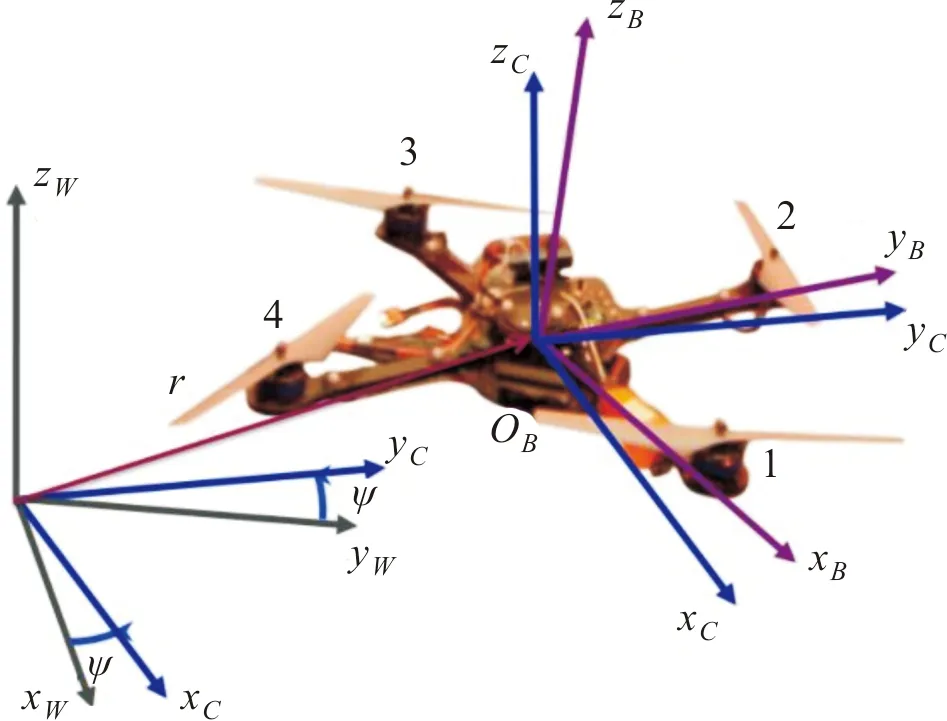
图1 四旋翼无人机空间坐标系

ω=pxB+qyB+γzB

(1)

式中：p,q和γ为3个坐标方向的角速度分量。

每个转子都有一个角速度ωi，并产生一个力Fi和力矩Mi：

(2)

式中：kF和kM分别为力系数和力矩系数。

现实实践中，与刚体动力学和空气动力学相比，电机动力学反应时间相对较快，因此假设它们可以瞬间实现，将系统的控制输入以u表示，其中u1是u2,u3,u4的合力，并将转子转速表示为[18]：

(3)

式中：L为从旋翼旋转轴到四旋翼中心的距离。

四旋翼无人机质心，在空间坐标系中每一时刻的位置向量用r表示。作用在四旋翼无人机系统上的力主要是-zW方向上的重力mg，和来自zB方向上每个转子的合力u1。于是，将控制四旋翼无人机质心加速度的牛顿运动方程表示为[19]：

(4)

式中：m是四旋翼无人机质量；g是地球重力加速度。

根据欧拉方程，构建四旋翼无人机角加速度模型：

(5)

式中：Γ是沿着xB-yB-zB轴质心方向的惯性矩阵。

于是，四旋翼无人机的空间状态可由其质心位置、速度、方向以及角速度参数联合表示：

(6)

2 四旋翼无人机飞行航迹建模

采用分段多项式，将四旋翼无人机每一段飞行航迹pi(t)表示为N阶多项式[19]：

pi(t)=αTβ(t),t∈[0,Tc]

(7)

式中：α∈R(N+1)×3为系数；Tc为四旋翼无人机飞行持续时间；β(t)=(1,t,t2,…,tN)T为基函数。

对于奇阶多项式航迹，由于N为奇数，系数矩阵与边界条件之间的映射是双目标的，pi(t)的(N-1)/2阶导数为：

(8)

令d(t)=B(t)α，则有：

(9)

(10)

式中：当N为奇数时，A(Tc)是方阵，否则A(Tc)为超定阵；A(Tc)=(BT(0),BT(Tc))T为2[(N+1)/2]行(N+1)列的映射矩阵。

实际上A-1(Tc)的所有项都是Tc的幂函数，应用高斯消去法可得到它的解析形式，当在线计算A-1(Tc)时，为了不再需要耗时的操作，需预先计算相关的系数矩阵E，F，G，U和W∈RS×S，其中S=(N+1)/2[20]：

(11)

(12)

(13)

(14)

(15)

当在线计算时，只需通过式(6)进行：

(16)

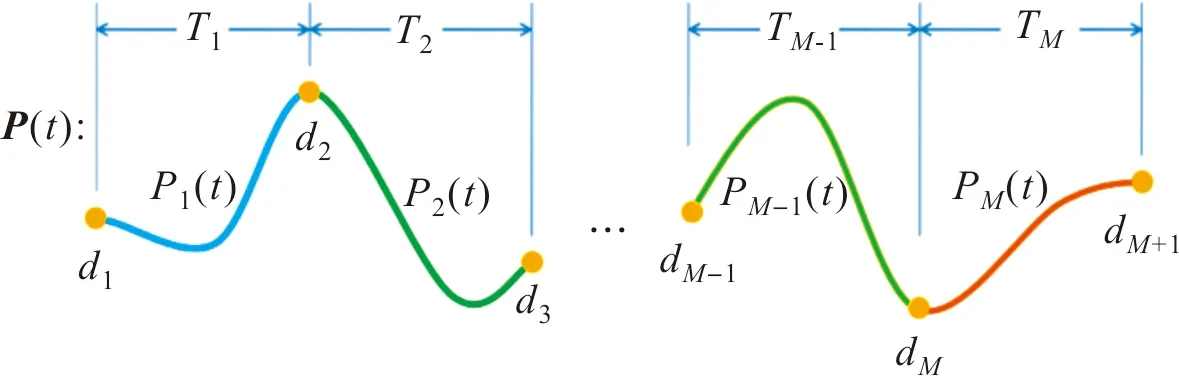
图2 采用分段多项式表示的飞行航迹

3 飞行航迹平滑估计

四旋翼无人机在有障碍物的空间顺利通过的一个重要指标要求是无人机与预定航迹的最小偏差。无人机与预定航迹的偏差评价可通过时间变量的一种多项式运算获得。

根据四旋翼无人机的运动方程式(4)可知，其控制信号(推力和推力力矩)依赖于位置r(t)∈r的4阶导数r(4)(t)。为此，通过一组给定点的光滑曲线，采用一种变分方法来最小化r(4)(t)[1]：

(17)

式中：p*(t)为两个后续航迹点之间所期望的航迹。

将式(17)用欧拉-拉格朗日微分方程表示为：

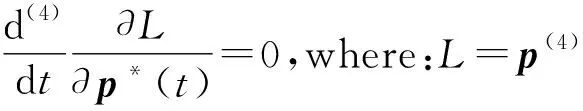
(18)

可将所期望的规避航迹指定为时间的7次幂多项式，例如：

(19)

多项式pi(t),i=1,2,…,n(n为要通过的控制点数),必须满足一定的约束条件才能确定所有的参数αij(i=1,2,…,n;j=0,1,…,7)。其中，可由式(20)确保多项式能够在各航迹点上移动：

(20)

式中：i=1,2,…,n。此外，在初始位置和最终位置，四旋翼无人机的速度、加速度和悬停值均为零，引入式(21)和式(22)以平滑相邻多项式：

(21)

(22)

于是，可将含有未知数αij的式(20)～式(22)写成如式(7)的矩阵形式：

A=αTb

(23)

式中：A为8n×8n的矩阵；α为所需参数；b为8n×3的矩阵。

4 在线规避航迹优化

典型梯度轨迹最优(gradient-based trajectory optimization, GTO)[20]，作为当前主要的航迹生成方法，常与欧氏符号距离场(euclidean signed distance field，ESDF)[21]相结合，可实现无人机航迹的自主规划。但在欧氏符号距离场中，面对临时出现、不可避免的障碍物，其周围的梯度会产生较大差异。当四旋翼无人机穿过通过欧氏符号距离场表示的区域时，欧氏符号距离场的梯度会在这些障碍物附近发生突变，使得航迹无法顺利绕过这些障碍物。

通常情况下，欧氏符号距离场难以及时应对这些临时出现、不可避免的障碍物，尤其是在复杂的现实环境中。为了进一步解决这一问题，引入额外的参量信息，加入距离代价、碰撞代价以及速度和加速度惩罚项，构建四旋翼无人机在线规避航迹优化模型。将整个飞行航迹细分为b个控制段，以更有效地评估不同阶段的规避成本。对于临时出现障碍物的阶段，将该段航迹重新参数化为{Q0,Q1,…,QN}个控制点。

四旋翼无人机在线规避航迹优化模型由两个不同的部分组成。第一部分，如图3所示，针对四旋翼无人机预定飞行航迹(绿色曲线)，根据A*或RRT*等传统算法获得规避当前障碍物的几何引导路径(黄色折线)，通过几何引导将初始航迹吸引到自由空间以构成规避航迹。将该部分的优化目标函数构建为：

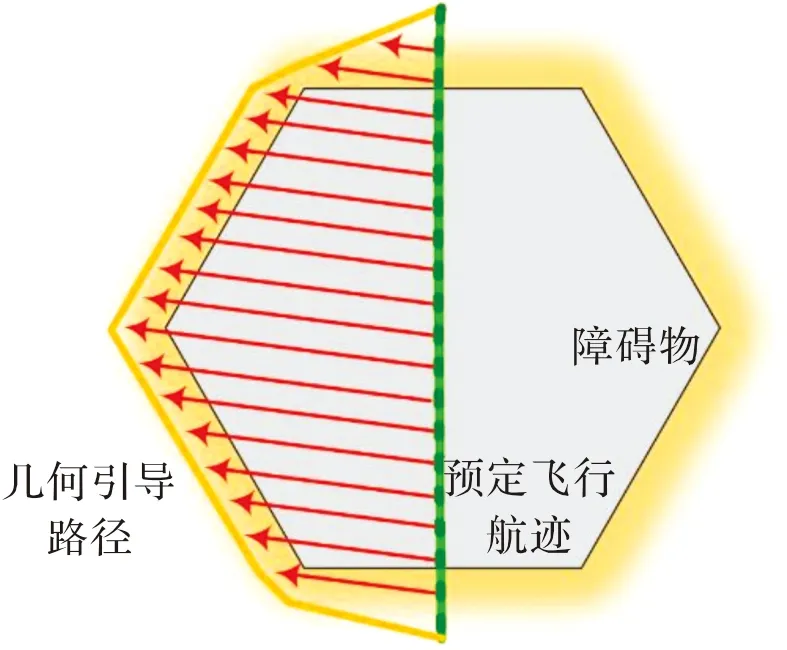
图3 在线规避航迹生成

fp1=λ1sfs+λ1gfg

(24)

式中：fs为飞行轨迹的平滑代价；fg为惩罚路径与b′条航迹之间的距离代价；λ1s和λ1g分别为代价系数。

参考文献[21]，将平滑代价fs设计为一个弹性带代价函数[21]：

(25)

由于b′段航迹的形状是由各控制点精细控制后形成的，利用这一性质来简化距离代价fg的设计。对于每个控制点Qi，在其引导路径上分配一个关联点Gi，该关联点Gi沿引导路径均匀采样。于是，将距离代价fg定义为这些关联点之间的欧式距离的平方和：

(26)

在该部分，欧氏符号距离场沿航迹的梯度变化平稳，如图3中的红色箭头所示，目标函数的梯度将与航迹向自由空间演化方向相一致。

第二部分，如图4所示。

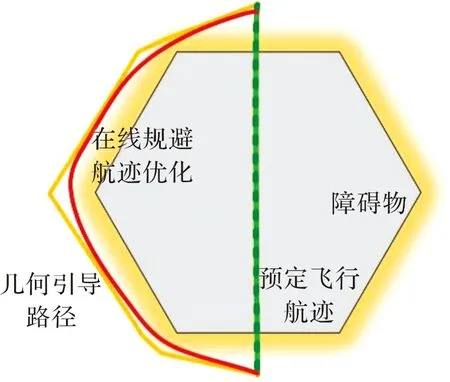
图4 在线规避航迹优化

根据第3节的航迹平滑估计方法，对飞行航迹的平滑度、动态可行性进一步优化，并在此基础上构建在线规避航迹优化目标函数：

fp2=λ2sfs+λ2cfc+λ2d(fv+fa)

(27)

式中：fc为欧氏符号距离场中评估的碰撞代价，当飞行航迹接近障碍物时，碰撞成本将迅速增长；fv和fa用于惩罚不可行的速度和加速度；λ2s，λ2c和λ1d分别为代价系数。其中，将碰撞代价fc表示为各控制点上障碍物的排斥力的累计函数：

(28)

式中：d(Qi)为控制点Qi与障碍物之间的距离函数；Fc(·)是一个可微分的潜在代价函数，与表示障碍物清除的阈值dthr相关。

(29)

为了使四旋翼无人机飞行稳定，将对超过最大允许速度或加速度的飞行航迹进行惩罚。

(30)

式中：ϑ为不同坐标轴方向的飞行速度(v)或加速度(a)，μ∈(x,y,z)。

基于F(ϑμ)，构建速度惩罚函数fv和加速度惩罚函数fa：

(31)

(32)

5 仿真分析

提出的航迹规划方法是在C++11中使用通用的非线性优化求解器NLopt4来实现的，并分别在仿真环境和真实环境中检验方法的有效性。设置在线规避航迹优化模型代价系数λ1s=9,λ1g=2.3,λ2s=10,λ2c=0.8,λ2d=0.01。

四旋翼无人机在未知环境下飞行时，由于感知范围有限，需要频繁地重新规划飞行航迹，即当预定飞行航迹与新出现的障碍物将发生碰撞时，需要在线进行航迹重规划，以确保一旦检测到任何碰撞，就有新的安全飞行航迹可用[23]。为此，构建一个未知环境以进行四旋翼无人机在线规避航迹规划仿真实验。仿真实验中，将整个空间环境设为未知灰色地带，四旋翼无人机具备半径为10 m的感知范围。在相同约束条件下，采用分段多项式，将每一段航迹表示为一个N阶多项式，通过文中方法在线规划获取最优规避航迹。不同阶多项式下的航迹变化如图5所示，选择较大的N虽然可以确保高阶连续性，与此同时也会增加计算时间和运算复杂度。

图5 不同阶多项式下的航迹变化

选取多项式阶数N=5，四旋翼无人机在线规避航迹规划结果如图6所示，其中，绿色曲线表示瞬时航迹方向，红色曲线表示多项式N=5时的最优在线规避航迹。面对非结构化未知环境、有限的感知范围以及较高的飞行速度，文中方法能够持续、快速地生成规避航迹。

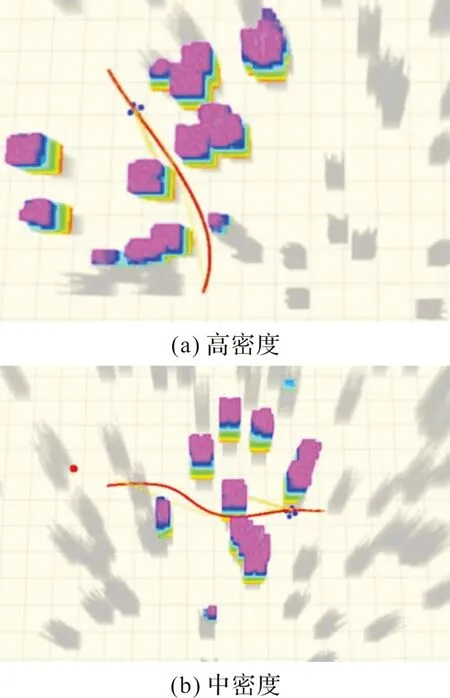
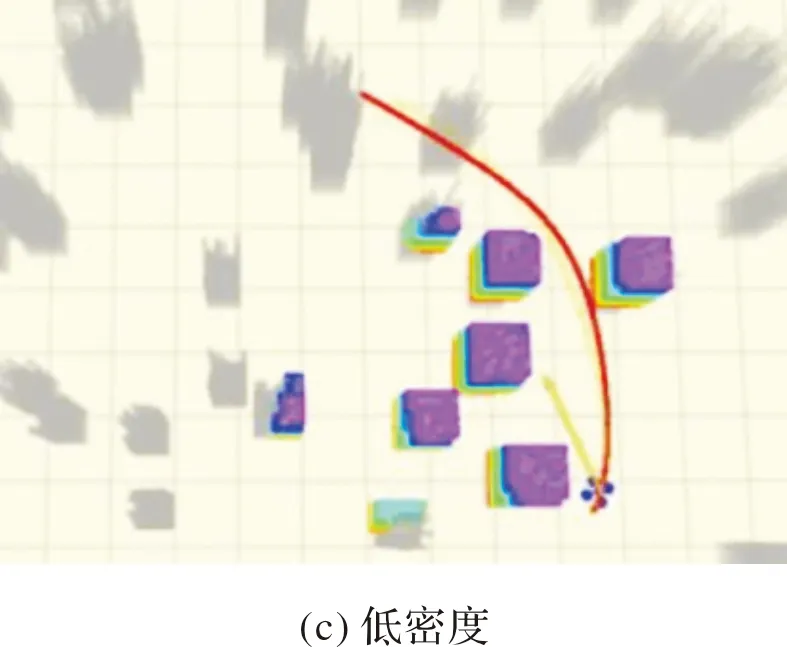
图6 四旋翼无人机在线规避航迹生成

为了客观地说明文中方法的有效性，将其与两种先进的方法real-time trajectory(RTT)[8]和teach repeat replan(TRR)[9]进行了仿真对比。对比实验分别在40 m×40 m×5 m地图上设置低密度、中密度和高密度3种复杂环境，四旋翼无人机最大速度和加速度限制分别设为3 m/s和2 m/s2。公平起见，运用相同的参考航迹[22]初始化所有方法，并将优化时间限制在15 ms以内，相关数据统计如表1所示，仿真效果如图7所示。对比结果可知，文中方法始终能够保持较高的成功率在未知环境中获得可行的规避航迹。相比较而言，其他两种方法的成功率随着环境复杂性的增加而降低，整体计算时间更长。

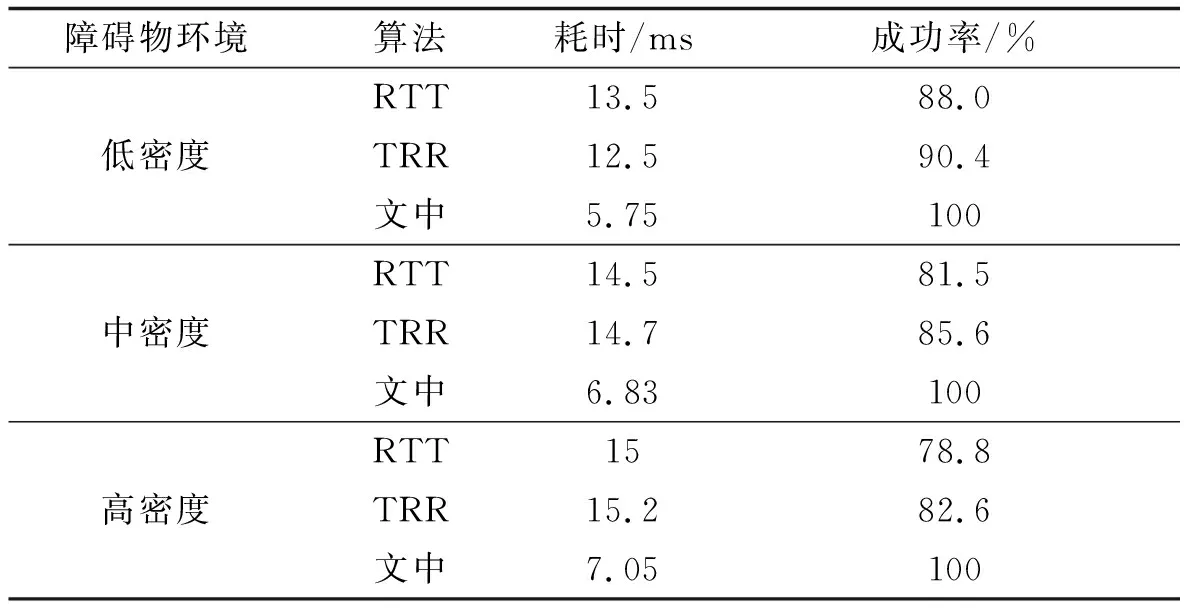
表1 不同复杂环境下3种算法仿真数据对比

图7 不同复杂环境下3种算法航迹规划效果

6 结论

提出了一种四旋翼无人机在线规避航迹规划方法。在分析四旋翼无人机空间运动的基础上，以其质心位置、速度、方向以及角速度参数联合构建运动模型。面向无人机在线避障需求，采用分段多项式对四旋翼无人机飞行航迹进行建模。针对四旋翼无人机预定飞行航迹，通过几何引导将初始航迹吸引到自由空间以构成规避航迹。结合航迹平滑估计，对规避航迹的平滑度、动态可行性进行优化，从而实现四旋翼无人机的在线规避和航迹重规划能力。

在复杂环境模型中，从计算时间、运算复杂度以及成功率等方面对比仿真表明，选择高阶多项式虽然可以确保高阶连续性，但也会增加计算时间和运算复杂度，文中方法相较于RTT算法和TRR算法运算耗时平均低54%、成功率平均高出15.8%，更适用于四旋翼的在线规避航迹规划。