半球谐振陀螺电路增益非对称分析及抑制方法

赵万良，江文杰，张天翔，樊 琦，邵添羿

（1.上海航天控制技术研究所，上海 201109；2.上海惯性工程技术研究中心，上海 201109）

半球谐振陀螺具有稳定的化学、物理性质，其力平衡模式在卫星、深空探索、潜艇等载体上已得到广泛应用[1]。力平衡模式控制下的半球谐振陀螺的测量范围和带宽较小，无法满足捷联惯导对陀螺仪的动态要求，全角模式半球谐振陀螺有着更大的测量范围和带宽，更加适用于捷联惯导、导弹制导等具有一定动态性能要求的应用场景。

不同于力平衡工作模式中被锁定在固定轴的驻波[2]，全角模式中驻波可以自由进动。由于驻波可能出现在360 °的任意方向，对陀螺的对称性提出了更高要求。这种对称性要求主要体现在表头的频差、阻尼不均匀、电极安装误差，以及检测和驱动电路的增益、相移非对称[3-7]。目前国内外针对陀螺非对称性提出了补偿或者校准的方法[8-11]，文献[12]从信号解调的角度分析了检测驱动电路增益非对称误差对驻波解算角度的影响[12]，但没有研究检测驱动电路非对称性对陀螺标度因子和零偏的影响。

本文针对全角模式中检测、驱动电路的增益和相移非对称，对驻波的进动特性进行理论分析，得到检测驱动电路非对称性对陀螺标度因子线性度和稳定度的影响机理，提出对0 °和45 °电极的检测以及驱动电路进行复用，该方法基本消除了两路的增益和相移非对称性，并通过仿真和实验验证了该方法的有效性。

1 增益与相移误差理论分析

1.1 陀螺动力学模型

带有非理想因素的半球谐振陀螺谐振子动力学模型可表示为[13]：

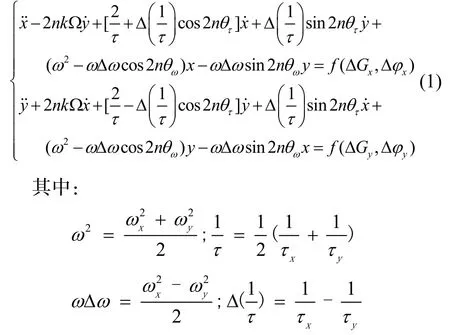
ωx和ωy为两个振动模态的谐振频率，θ ω为刚性频率简正轴，τx和τy为两个阻尼简正轴的时间衰减常数，k为进动因子，Δω为陀螺的频差，Ω 为外界输入角速度，当谐振子处于四波腹振荡状态时，n=1，ΔGx(ΔGy)和Δφx(Δφy)代表x(y)检测驱动电路的增益和相移非对称性，f(ΔGx,Δφx)、f(ΔGy,Δφy)为控制电极对谐振子的施力项。

式(1)包含了表头的频差和阻尼不均匀对陀螺的影响，而检测驱动电路的增益和相移非对称误差对陀螺的影响机理尚不明确，为进一步探讨f(ΔGx,Δφx)和f(ΔG y,Δφy)的具体形式，分别对检测端和驱动端的电路进行建模并代入到动力学模型进行分析。

1.2 检测电路增益与相移非对称误差分析

信号检测电路将陀螺的振动信号转化为可以利用的电信号，信号检测电路示意图如图1 所示。

图1 信号检测电路Fig.1 Signal detection circuitry

定义x和y检测电路的增益为Gx=KCVx K folx K difx KADx、G y=K CVyK foly K dify KADy，定义x和y检测电路的相移为Δφ x、Δφ y，检测到的振动信号分别记为xt、yt，检测信号满足式(2)。

当检测电路相移很小时，检测信号和陀螺振动信号之间的关系满足式(3)。

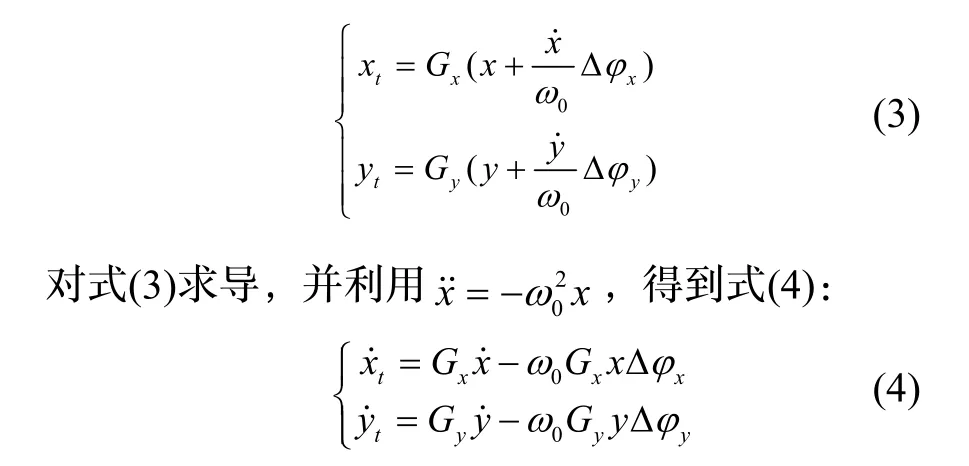
结合式(3)(4)得到式(5)：

对矩阵求逆，得到陀螺振动信号的表达式：

将式(6)代入到式(1)，得到含有检测电路增益和相移的半球谐振动力学模型：益和相移的动力学模型，将动力学模型转化为描述振型的慢变量方程[14]：

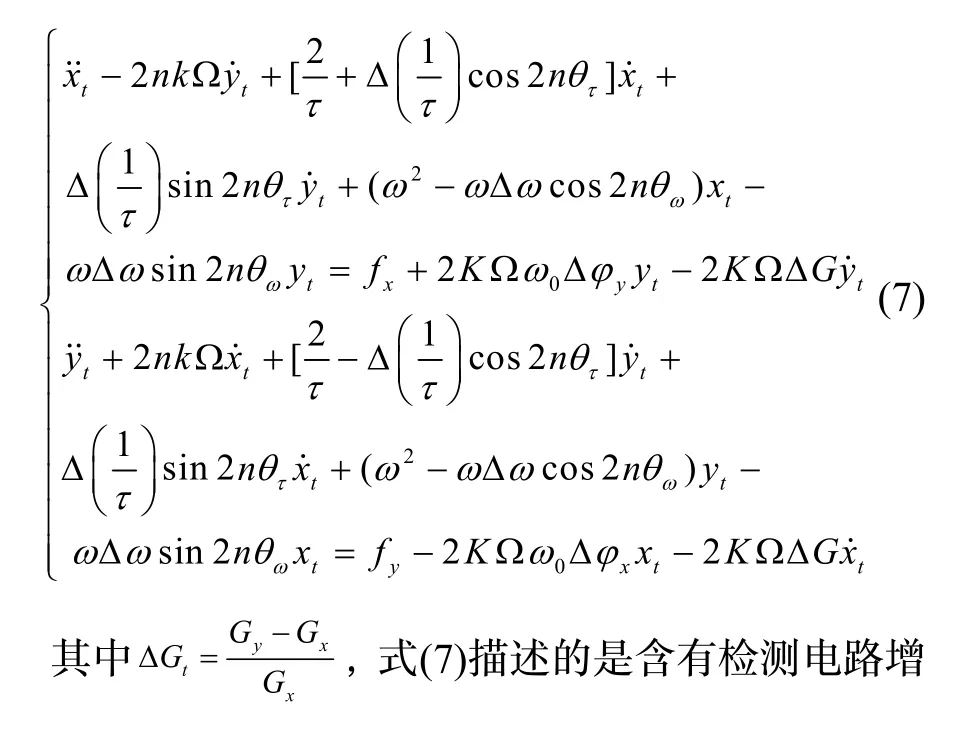
与检测驱动增益和相移有关的项为：

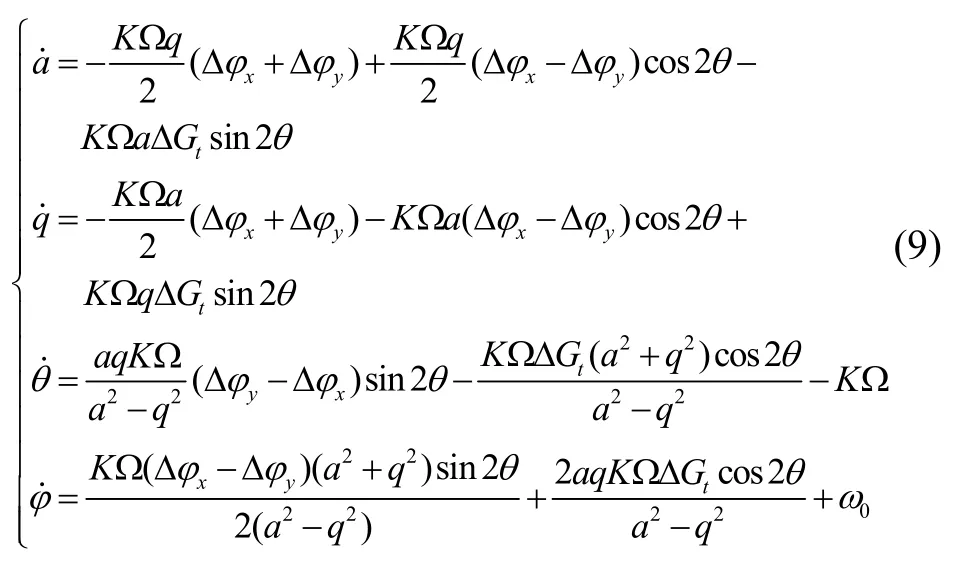
其中a、q、θ和φ分别为陀螺驻波的振幅、正交误差、进动角和相位，式(9)表示了检测电路的增益与相移非对称性对陀螺振幅、正交误差、驻波进动角和振动相位的影响，陀螺的标度因子由第三项决定，其中-KΩ 为半球谐振陀螺的驻波进动角速度，别代表检测电路增益和相移非对称性造成的影响。

1.3 驱动电路增益与相移非对称误差分析

半球谐振陀螺全角模式的控制环路包括频相跟踪环路、幅度控制环路、正交控制环路，陀螺的驱动信号为：

其中FE为幅度控制环路驱动力，F q为正交控制环路驱动力，Gc和Δφc表示0°驱动电路的增益和相移，Gs和Δφs表示45°驱动电路增益和相移。

引入驱动电路增益和相项后，增益和相移的非对称导致驻波产生漂移，记引入增益项后的驻波角度为θd，θd满足式(11)

将式(11)对时间求导，得到包含驱动电路增益与相移的驻波角度表达式

其中T=2π/ω，则等式右边第三项为零，可得

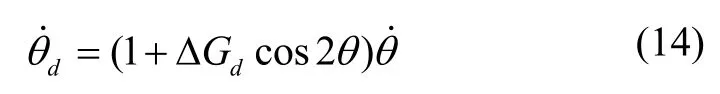
1.4 电路增益和相移误差对陀螺的影响

综合考虑检测和驱动电路增益与相移非对称对陀螺的影响，联立式(8)(14)，忽略二阶小量，得到包含检测驱动电路增益和相移非对称性的驻波进动角速度表达式：

因此全角模式下陀螺的零偏为：

标度因子为：

分析式(9)(17)可知，在标度因子的影响因素中与相移有关的项为相移非对称与正交误差量的乘积，当正交回路达到稳态后，该项的影响可以忽略。因此检测驱动电路非对称性对陀螺的影响主要体现在增益非对称。驱动电路增益非对称和检测电路增益非对称通过对陀螺振幅a和正交q的影响间接影响了陀螺的零偏，但在陀螺的闭环控制中，正交误差被抑制到接近 0，所以对零偏的影响可以忽略，但它们对标度因子则产生了直接影响，且驱动和检测电路的非对称性对标度因子的影响形式基本相同。根据4.1 节实测的增益非对称数据，按照式(17)绘制不同增益非对称下的标度因子与驻波角度的关系如图2 所示。

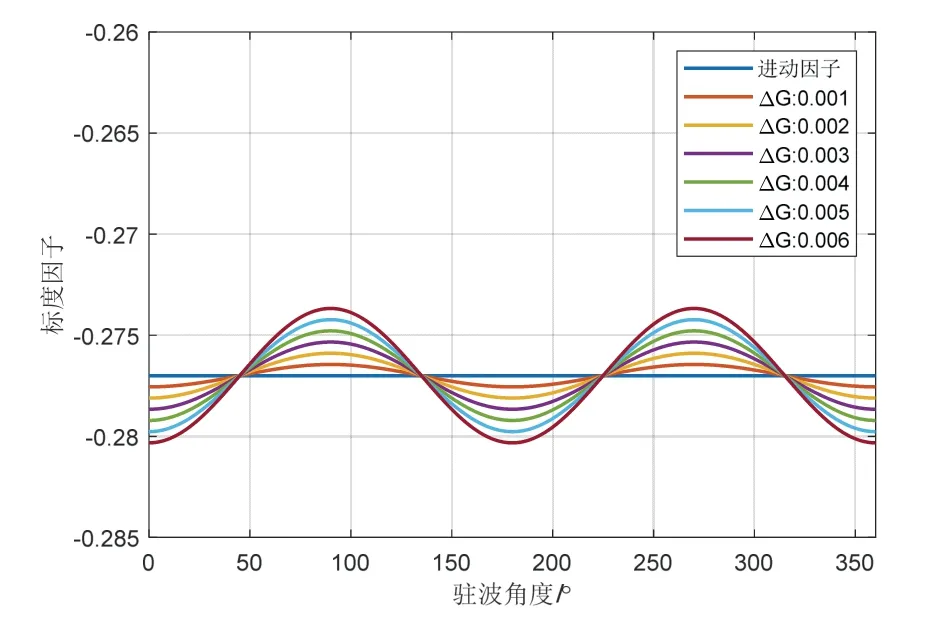
图2 标度因子和驻波角度的关系Fig.2 The relationship between the scale factor and the standing wave angle

由图2 可知，检测和驱动电路的增益非对称性会造成全角模式下陀螺的标度因子和驻波的角度有关，导致的标度因子的非线性；此外，非对称性往往还会随着温度的变化而变化，导致了标度因子的不稳定性。

2 增益非对称抑制方法

2.1 电路增益变化特性

在实际的电路中，以下因素会导致电路增益的非对称：

1.陀螺检测和驱动电路主要由运算放大器和阻容元件组成，不同检测驱动电路的器件参数值存在误差。

2.当外界温度变化时，由于温度梯度的存在，不同器件的温度变化不同，电阻、电容的值以及运算放大器的开环增益、带宽等参数随温度的变化呈非对称性。

由于检测驱动电路主要由运放与其外围器件构成，差分放大器的特性能较好反映电路增益变化规律，其结构如图3 所示。

图3 差分放大器结构Fig.3 The architecture of differential amplifier

令R1=R3，R2=R4，考虑增益带宽积，差分放大器的传递函数为

其中f0为运放的开环增益低频极点，Gbw为运放的增益带宽积，以OP470 和薄膜电阻为例，其参数如表1 所示。OP470增益带宽积随温度变化如图4所示。

表1 OP470 和薄膜电阻参数Tab.1 The parameters of OP470 and thin film resistance

图4 OP470 增益带宽积与温度的关系Fig.4 OP470 gain bandwidth product vs.temperature

令R1、R2、R3和R4的初始值相等，R2和Gbw的值随温度变化，根据式(18)绘制增益-温度变化图，由图5 可知，差分放大器增益变化与温度基本呈线性关系。

图5 差分放大器增益与温度的关系Fig.5 Differential amplifier gain vs.temperature

2.2 增益非对称抑制方法

根据第一章的分析结果，陀螺的检测和驱动电路的非对称会造成标度因子非线性和不稳定性，为解决这个问题，可以通过切换的方式使得两路信号共用检测和驱动回路来抑制增益非对称性，原理如图6 所示。

图6 驱动和检测电路单路复用原理图Fig.6 Single-way multiplexing schematic ofdrive and detection circuits

1.状态一：检测0°轴，驱动45°轴

2.状态二：检测45°轴，驱动0°轴

陀螺0°轴和45°轴通过同一个检测电路和驱动电路，单路复用的电路增益和相移非对称性满足式(19)：

由式(19)可知，单路复用理论上可以消除检测驱动电路的增益和相移非对称性，信号处理模块前后的反切换使得信号恢复为0 °和45 °信号，所以单路复用在减少电路硬件的同时不用改变信号处理的逻辑，原理图中的开关可以使用远高于陀螺谐振频率的切换信号，当切换频率大于或等于AD(DA)两倍采样率时，数字信号处理电路理论上可以获得与双路驱动检测相同的信号，因此不会对陀螺的角度变化带宽带来影响，实际中可以采用具有高切换频率的模拟开关器件，由FPGA 产生大于或等于AD(DA)两倍采样率的开关控制信号，单路复用的关键在于信号的切换，必须保证信号在切换过程中不互相干扰且能够完全复原。

3 仿真验证

为确定单路复用的可行性，在matlab 中搭建陀螺的控制模型，进行信号切换的功能性仿真并在全角模式下验证单路复用对标度因子非线性和稳定性的提升。

根据式(1)在matlab 中建立陀螺数学模型并作为控制系统的受控对象，用160 kHz 的方波作为开关控制信号将0 °轴和45 °轴的检测信号切换到同一个检测通道，信号切换结果如图7 所示

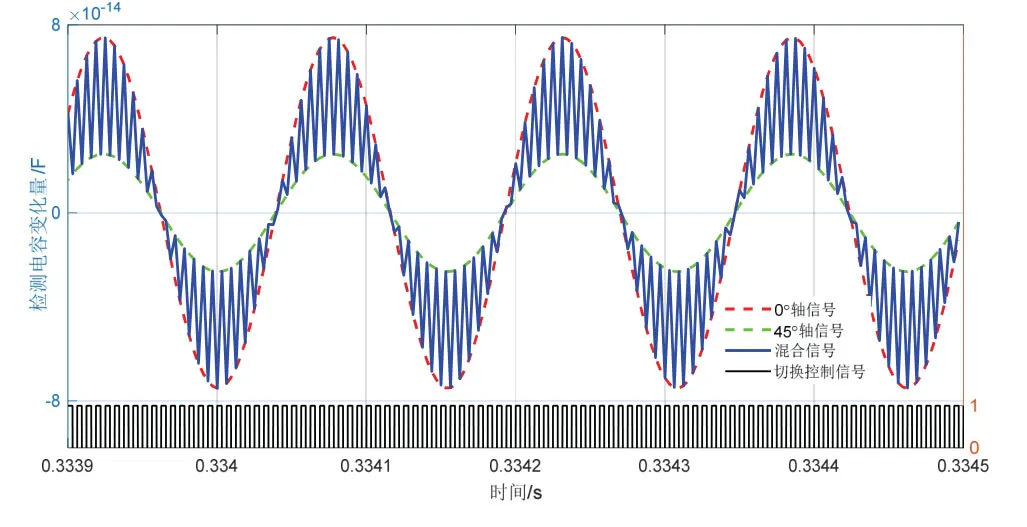
图7 检测电路前端信号切换Fig.7 Detects front-end signal switching in the circuit

模拟信号经过AD 采样后变为数字信号，在数字处理器中对该信号进行反切换，将其还原为0 °轴信号和45 °轴信号，AD 采集的信号以及信号的还原过程如图8 所示。

图8 检测电路后端信号还原Fig.8 circuit back-end signal restoration

驱动端的信号切换过程与检测端类似，所有切换的控制信号为同一个信号，保证信号切换的同步性。

根据1.3 节结论，检测驱动非对称对陀螺的影响主要体现在增益非对称，由下文中4.1 节的增益非对称温度实验可知在25℃到85℃的温度范围内，增益非对称最大值为5.8‰，根据理论以及实验结果，在仿真中设置检测驱动增益非对称GΔ 为6‰，其余仿真参数如表2 所示。

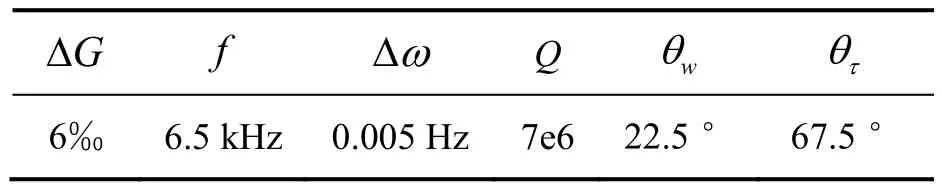
表2 陀螺双路检测驱动与单路复用仿真参数Tab.2 Gyro dual detection drive and single multiplexed simulation parameters

其中，f为陀螺谐振频率，Δω为陀螺频差，Q为陀螺的品质因数，θw和θτ分别为陀螺频率轴和阻尼轴，以上参数按照接近陀螺真实情况设置；模拟外界角速度，分别设置为 ±1 °/s、±1 0°/s、±5 0°/s、±100°/s，记录全角模式下陀螺角度的输出，对比双路检测和单路复用情况下标度因子的线性度，陀螺的输入输出以及拟合曲线如图9-10 所示。

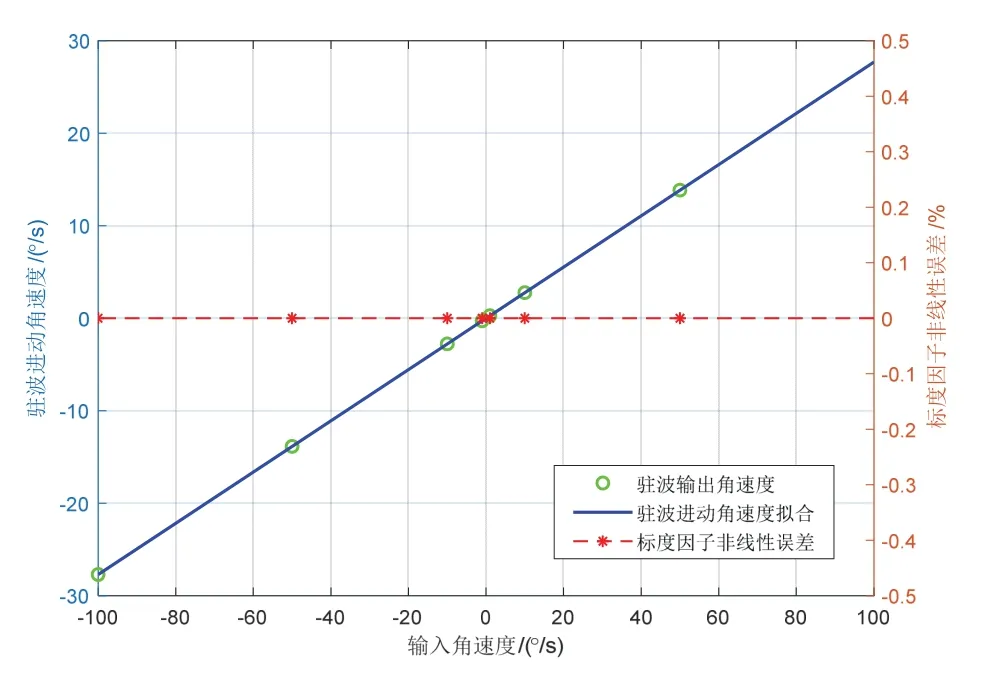
图9 双路检测驱动标度因数仿真Fig.9 Dual-channel detection drives scale factor simulation

图10 单路复用标度因数仿真Fig.10 Single multiplexed scale factor simulation

全角模式标度因子非线性度的计算方法为：

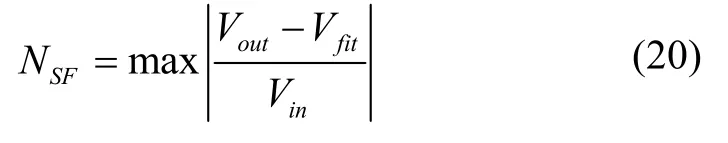
仿真结果显示双路检测驱动的标度因数非线性为296.7 ppm，单路复用的标度因数非线性为0.3 ppm，提升了约4 个数量级。

按照4.1 节增益非对称实验结果设置温度从25℃到85℃时的增益非对称性参数，共10 个温度点，如表3 所示。

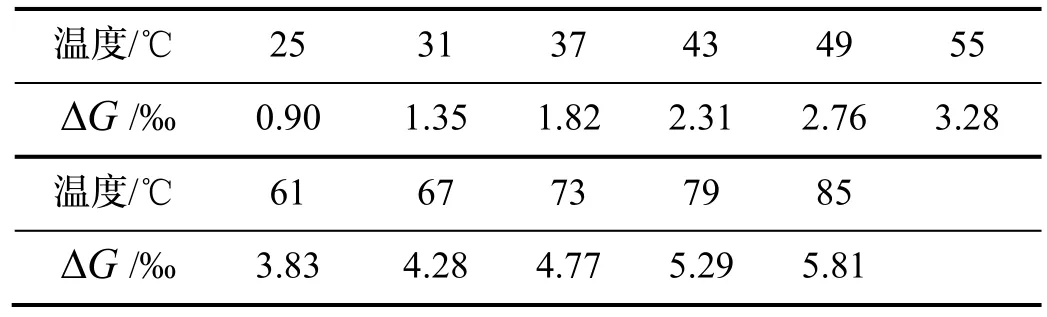
表3 不同温度下的增益非对称参数Tab.2 Gain asymmetrical parameters at different temperatures

不同温度下设外界输入角速度分别为±1°/s、±10°/s、±50°/s、±100°/s，计算不同温度下的标度因数，对比双路检测驱动和单路复用的标度因数稳定性，仿真结果如图11 所示。

图11 标度因子与温度的关系Fig.11 The relationship between the scale factor and temperature

双路检测驱动和单路复用的标度因子分别变化了970.7 ppm 和0.1 ppm，降低了约5 个数量级。

以上仿真结果表明，检测和驱动电路的单路复用基本可以消除检测增益非对称性对标度因子线性度和稳定性的影响。

4 实验验证

4.1 电路增益非对称性实验

为确定电路增益非对称性与温度的关系，用正弦信号测试陀螺0 °和45 °的驱动检测电路增益，原理如图12 所示。

图12 电路增益检测原理Fig.12 The schematic of circuit gain detection

将陀螺检测驱动电路放进温箱，设置温度变化程序为：初始值25℃，保持10 分钟后以1℃/min 的温变速率上升到85℃并保持十分钟，然后以-1℃/min 的温变速率下降到初始值，记录两路检测驱动电路的增益，并做归一化处理，结果如图13 所示。

图13 电路增益非对称温度实验Fig.13 Circuit gain asymmetric temperature experiment

由图16 可知，0 °和45 °检测驱动电路的增益在25℃存在0.9‰的差异，随着温度的上升，两路的增益非对称性也逐渐增大，且近似呈线性关系，到85℃时增益非对称达到了5.8‰。

4.2 控制电路单路复用实验

为了进一步验证理论分析和仿真结果，根据2.2节提出的单路复用方法设计驱动检测切换电路并测试单路复用下的CV 输出，如图14 所示。

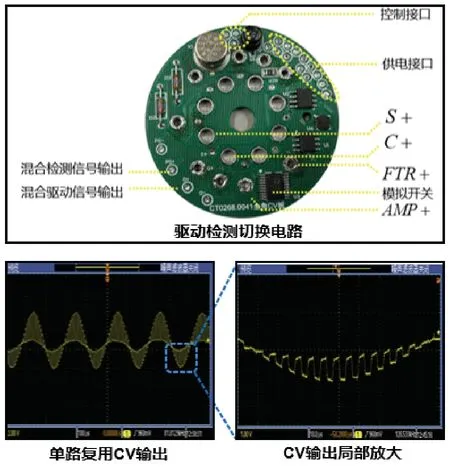
图14 单路复用切换电路及CV 输出Fig.14 Single multiplexed switching circuit and CV output

对比图14 和图7 可知，单路复用下的CV 输出与仿真结果基本相符。接下来搭建陀螺测试平台，分别开展双路检测驱动和单路复用的转台实验，先后将两种硬件状态的陀螺和控制电路固定在转台上，控制转台以±1 °/s,±5 °/s,±10 °s/ ±20 °/s,±50 °/s 的转速旋转，当转台转速稳定后，记录每个转速下60 s 的角度输出数据，测试平台如图18 所示。

图15 是测试转台正向输入20 °/s 时，双路检测驱动与单路复用的角速度-方位角曲线。

图15 半球谐振陀螺测试平台Fig.15 Hemispheric resonant gyroscope test platform

由图16 可知，与双路检测驱动相比，单路复用将角速度漂移降低了82%，根据式(15)，剩余的角速度漂移为与阻尼不均匀有关的零偏。按照式(20)计算双路检测驱动与单路复用的标度因数非线性，结果如图17 所示。

图16 双路检测驱动与单路复用的角度-角速度对比Fig.16 Angular-angular velocity comparison between dual detection driver and single multiplexed

图17 双路检测驱动与单路复用的标度因数非线性对比Fig.17 Nonlinear comparison of scale factor of dual detection driver and single multiplexing

由图17 可知，单路复用将标度因数非线性从6%降低到了1.3%，与角速度漂移一样，如果需要进一步降低标度因数非线性，需要解决谐振子阻尼不均匀问题。

5 结论

本文首先推导了含有检测驱动电路非对称项的半球谐振陀螺非理想动力学模型，得出检测驱动电路非对称对陀螺的影响主要体现在增益非对称的结论；然后通过仿真得到在6‰检测驱动增益非对称下标度因子的非线性和不稳定性分别为 296.7 ppm 和970.7 ppm，提出一种单路复用方法抑制电路的增益非对称，仿真结果显示通过单路复用可将增益非对称带来的标度因数非线性和不稳定性分别降到0.3 ppm 和0.1 ppm，证明了方法的有效性；接下来开展温度实验证明了电路的增益非对称与温度基本呈线性关系；最后开展双路检测驱动与单路复用的对比实验，实验结果显示单路复用将角速度漂移降低了82%，将标度因数非线性从6%降低到了1.3%，结合理论分析可知剩余的误差主要取决于谐振子的阻尼不均匀；根据仿真和实验结果得出结论：单路复用可以有效解决全角模式的电路增益非对称问题。