锁相环相位误差对半球谐振陀螺零偏影响分析与校准

赵万良，夏 昕，成宇翔，杨 浩，王 伟

（1.上海航天控制技术研究所，上海 201109；2.上海惯性工程技术中心，上海 201109

半球谐振陀螺具有结构简单、体积小、精度高、寿命长、可靠性高等特点，被誉为最具潜力的哥氏振动陀螺，目前精度已达到惯性级并成功运用于各个领域[1,2]。力平衡模式半球谐振陀螺的工作状态稳定，其稳定性和精度极高，特别适用于卫星、深空探测飞船、太空望远镜等转动速率较小但要求测量噪声低的应用场合。

半球谐振陀螺的研制过程，从表头到控制系统都会存在一些非理想误差源，制约了半球谐振陀螺精度的进一步提高。国内外学者从不同角度进行了误差分析和抑制方法研究，文献[3-5]从谐振子Q值、频差、温度漂移角度进行了研究，文献[6]从共用电极导致的信号耦合角度进行了研究。但是现有文献对误差的研究主要集中在陀螺表头，对控制电路信号的变形和耦合研究较少。

高精度半球谐振陀螺控制时，要求谐振频率和相位跟踪得极其准确，通常做法是采用高精度锁相放大环路（PLL）实现频率和相位的实时跟踪。但是由于热噪声、机械颤动所引起的振荡频率抖动以及其他误差源引起的相位抖动，锁相环路跟踪信号必然存在误差[7-9]。同时检测到的信号经过前级放大电路和滤波电路必定存在相位延迟，使得本地参考信号相位作为驱动调制载波相位时与陀螺的实际振动信号相位Ωz不一致，本文在后续表述中统一称为锁相误差。这种锁相误差将对陀螺零偏产生影响[9,10]。本文对该影响进行了理论分析和仿真实验验证。针对锁相误差的校准，文献[9]提出增加载波进行环路相位的解调和校准。文献[10]通过改变正交耦合的正负极性，根据力平衡和正交控制力计算相位差并补偿。基于载波的方法需要合理选择载波的频率和相位，否则会引入解调误差。改变正交耦合正负极性的方法在MEMS 陀螺上可以通过改变直流电压实现，但是对于八电极结构的半球谐振陀螺，该方案实施比较困难，频率主轴的位置很难准确改变。本文提出了一种基于幅度控制力的锁相误差校准方法，该方法简单易行，不需要额外的电极，实验结果验证了该方法的有效性。

1 锁相误差对零偏的影响分析

1.1 力平衡模式控制系统和锁相环路基本原理

半球谐振子的运动可等效为0 °和45 °上一组简并模态的振动。由于阻尼不均匀和频率裂解，两个模态的振动相互耦合，考虑了耦合的非理想谐振子动力学方程[11,12]为：

其中，Fx为x轴的静电驱动力，Fy为y轴的静电驱动力，为y轴受到的科里奥利力。弹性耦合系数kxy（kyx）和阻尼耦合系数cxy（cyx）不为0，两个轴分别受到另一个轴的弹性耦合力和阻尼耦合力。考虑到y轴上的振动幅度相对x轴很小，因此忽略y轴对x轴振动的影响。

x轴做理想的正弦振动，振幅为Ax，谐振频率为ω，振动相位为φx。y轴的振动分解为振幅为b的与x轴同相位的振动，和振幅为n的与x轴相位相差90 °的振动。x和y轴的振动位移表示为：

力平衡模式下，控制系统共有四个环路，分别为幅度控制环路、力平衡控制环路、正交控制环路和锁相环路。幅度控制环路用于维持陀螺的持续振动，使x轴振幅保持恒定；力平衡控制环路用于检测外界进动角速度，并施加与进动角速度成正比的控制力，使得驻波控制在固定方位；正交控制环路用于抑制正交振动，减小两个模态的频差；锁相环路用于跟踪检测信号的频率和相位，为信号解调和其他环路的驱动调制载波提供本地参考信号。

两件套结构的半球谐振陀螺因其产品的尺寸、重量和功耗（Size Weight and Power consumption,SWaP）特性上的优势，成为热门发展方向之一。对于两件套结构半球谐振陀螺表头，谐振子外侧有八个电极，幅度控制力施加在x轴方向的电极上，力平衡控制力和正交控制力经过合成同时施加在y轴方向的电极上。幅度、力平衡、正交控制力的幅度分别用Famp、Fftr、Fquad表示。控制系统框图如图1 所示。

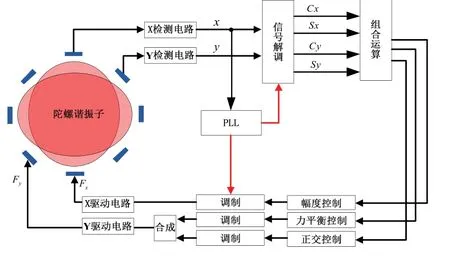
图1 力平衡模式控制系统框图Fig.1 The block diagram of the force rebalanced mode control system

典型的锁相环路如图2 所示，主要由鉴相器、低通滤波器、压控振荡器和分频器组成。输入信号的相位为φi，鉴相器对输入信号和分频器输出信号进行相干解调，解调后的信号经过低通滤波器得到输入信号和分频器输出信号之间的相位差φe，压控振荡器受到与该相位差成正比的电压信号的控制，输出经过调节的相位φo，理想情况下，经过锁相环路的调节，φ e最终被控制到0，φo与φi一致。

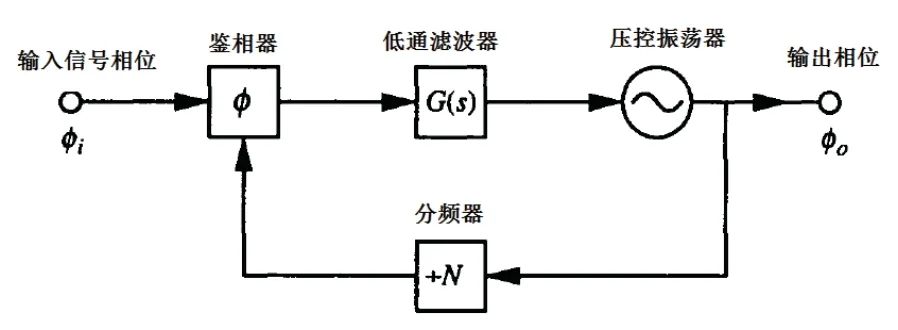
图2 锁相环基本原理框图Fig.2 Basic principle block diagram of phase locked loop

文献[7,8]指出，由于热噪声和其他原因，锁相环路输出的本地参考信号相位可能存在抖动和常值误差，使之与陀螺的实际振动信号相位不一致。记锁相误差为φr，锁相环路输出的相位为（ω t+φ x+φr），Fquad=G y GVF Vquad(-cos(ω t+φ x+φr))。

1.2 锁相误差对陀螺零偏的影响

对于两件套结构的半球谐振陀螺，力平衡控制力和正交控制力同时施加在y轴方向的电极，因此在引入锁相误差时，对这两个控制力同时考虑。通过分析施加在y轴方向的合成力，来分析锁相误差对力平衡和正交控制力的影响及零偏、标度因数等指标的变化。

力平衡控制环路根据检测到的y轴同相振动分量的振幅b，经过PI 控制器输出控制量Vftr，该控制量与锁相环路的输出相位(ω t+φ x+φr)调制，并经过驱动放大电路和电压到力的转换GVF成为控制力Fftr=G y GVF Vftrsin（ω t+φ x+φr）。类似地，正交控制环路根据检测到的y轴正交振动分量的振幅n，经过PI 控制器输出控制量Vquad，该控制量与锁相环路的输出相位（ω t+φ x+φr）调制，并经过驱动放大电路Gy和电压到力的转换GVF成为控制力。将控制力Fftr和Fquad代入y轴的动力学方程(1)有：

根据式(3)，存在锁相误差φr时，力平衡和正交控制力相互耦合，均产生了与原方向正交的控制力，此时的控制量表示为：

其中，ε为介电常数，S为电容极板面积，d0为无振动时初始电容极板间距离，V dc为使用一倍谐振频率控制时的直流电压偏置。

此时陀螺的标度因数和零偏表示为：

可见，标度因数被乘以了锁相误差的余弦值；零偏多了与频差和频率轴方位角相关的弹性耦合项，且通常在计算零偏时会使用固定的标度因数SF0，造成零偏中与阻尼相关的项也发生了微小的漂移。

为定量研究标度因数和零偏对锁相误差变化的灵敏度，进行了锁相误差连续变化的数值仿真，如图3所示。参考真实陀螺参数，设置两模态Q值差20%，阻尼方位角10 °，频率轴方位角8 °，两模态频差0.001 Hz～0.003 Hz。设定锁相误差的变化范围为-10 °～10 °。电容极板面积25 ×10-6m2，初始电容极板间距离150 ×10-6m，直流电压偏置100 V，进动因子0.277。

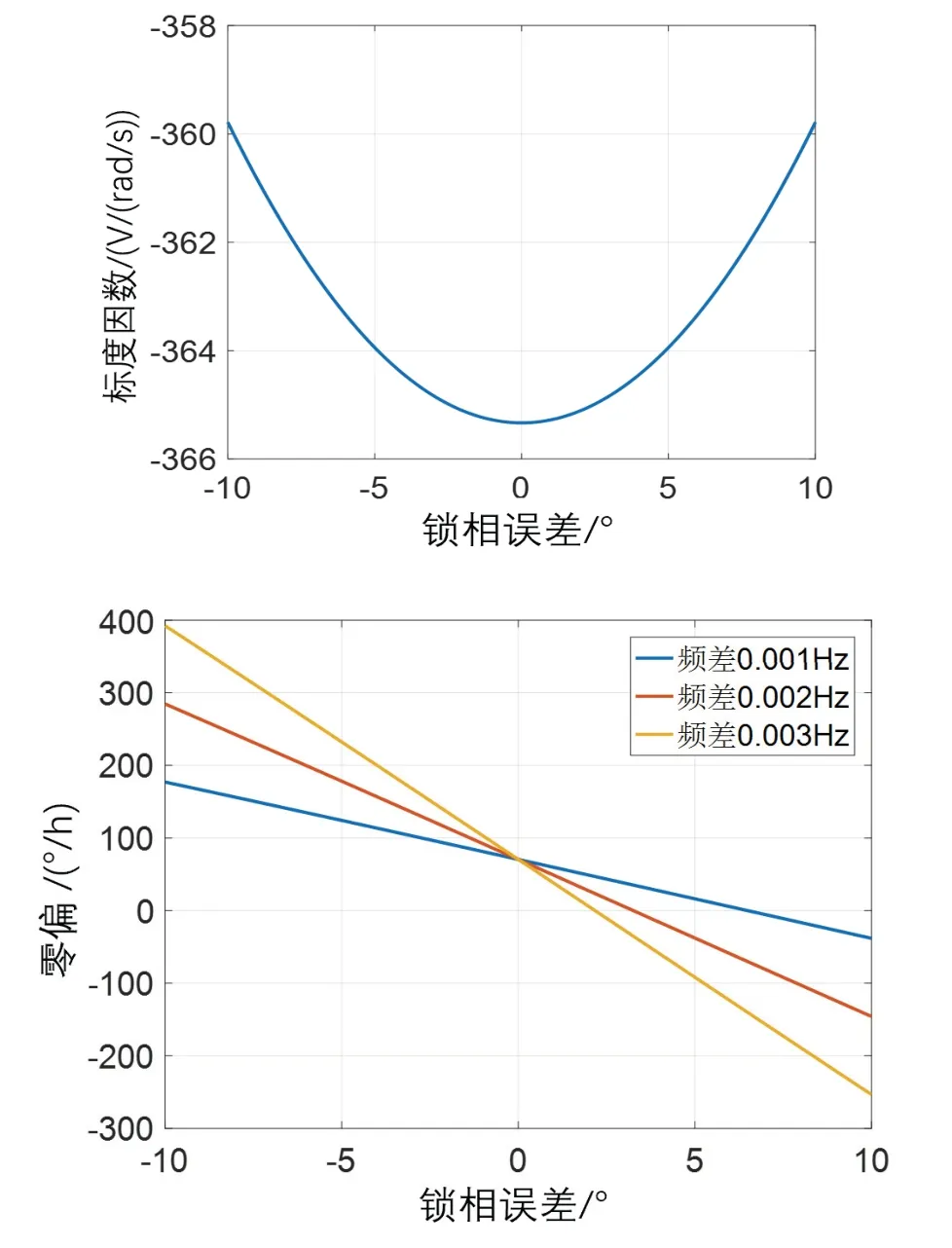
图3 标度因数和零偏随锁相误差 φ r的变化Fig.3 The relationship between scale factor,bias and phase-locking error

仿真结果显示：标度因数对锁相误差比较敏感，在1°处对锁相误差的敏感系数为152 ppm/°。零偏对锁相误差非常敏感，频差为0.001 Hz 时，零偏对锁相误差的敏感系数为10.8704 °/h/°，频差为0.003 Hz 时，零偏对锁相误差的敏感系数为32.3970 °/h/°。且频差越大，零偏对锁相误差越敏感。

可见，锁相误差对标度因数影响有一定影响，对零偏的影响不容忽视。由式(7)可知，影响该项零偏的因素主要是锁相误差和与频差、频率轴方位角相关的正交耦合。当锁相环路不稳定，电路相移随电路板温度变化时，这种由于锁相误差φr的波动带来的零偏波动将更加复杂。因此，需要尽量降低锁相误差φr以减小正交耦合。

2 常值锁相误差的校准

考虑到锁相误差也会对幅度控制环路造成影响，本文提出基于幅度控制量极小值的方法校准锁相误差，并在锁相环路输出端或驱动调制端进行相位补偿。

幅度控制环路根据检测信号x的振幅Ax与目标振幅A0的差值，经过PI 控制器输出控制量Vamp，该控制量与锁相环路的输出相位ω t+φ x+φr调制，并经过驱动放大电路和电压到力的转换GVF成为控制力Famp=G x GVFVamp(-sin(ω t+φ x+φr))。如1.1 节所述，由于y轴的振动很小，忽略其对x轴振动的影响，只考虑x轴电极上施加的幅度控制力。将x轴的振动位移方程(2)和其各阶导数、控制力Famp代入动力学方程(1)有：

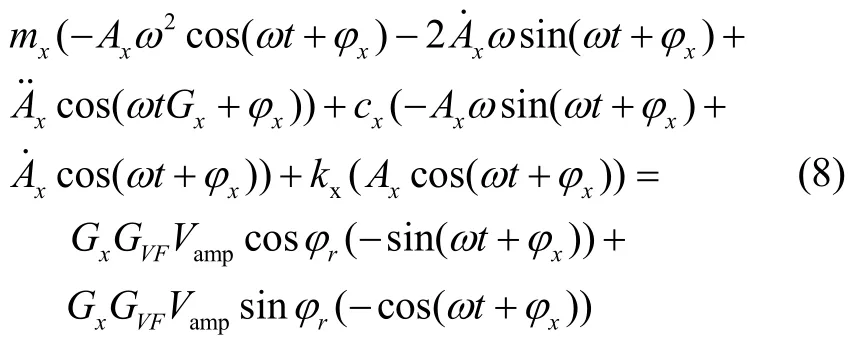
幅值稳定时，幅值变化率和二阶导数均等于0，可以得到幅值稳定时的陀螺幅度控制量。方程右边的第一项用于抵消方程左边的阻尼项，当存在锁相误差φr时，该项幅度控制力被乘以了略小于1 的系数cosφr，使得所需的控制量Vamp增大。第二项是与振动位移x同相的力，由于静电负刚度效应，该项会导致谐振频率ω的变化，与谐振子本征频率ωd不一致。幅值稳定时幅度控制量Vamp和谐振频率ω表示为：

为定量地研究幅度控制力对锁相误差变化的灵敏度，进行了锁相误差连续变化的数值仿真，如图4 所示。

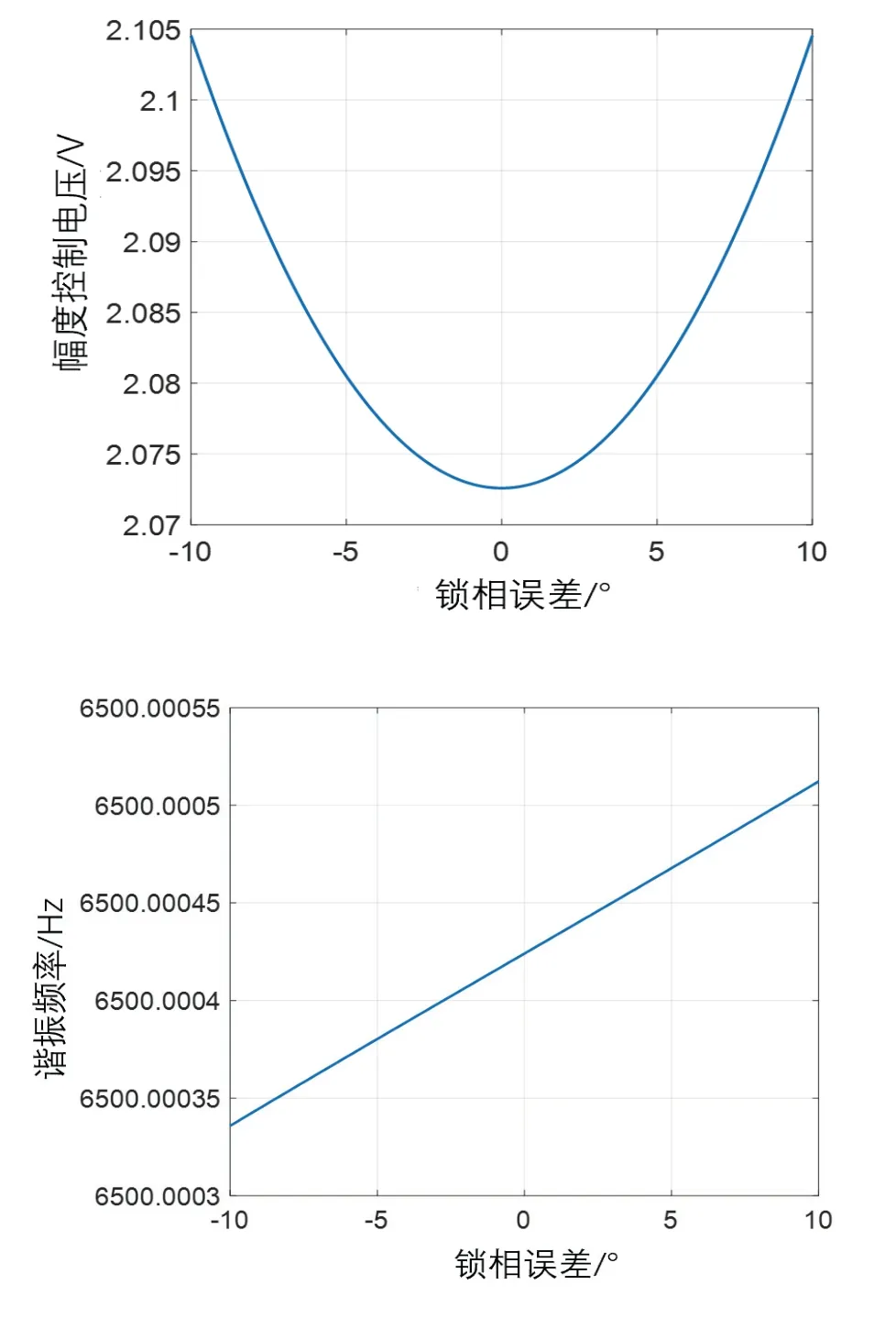
图4 幅度控制电压和谐振频率随锁相误差 φ r的变化Fig.4 The relationship between amplitude control voltage,resonant frequency and phase-locking error

可见，幅度控制电压在1 °处对锁相误差的敏感系数为152 ppm/°，在10 °处对锁相误差的敏感系数为2900 ppm/°，可以用来进行锁相误差的标定和补偿。而谐振频率对锁相误差不太敏感，变化了1.35 ppb/°，可以忽略。

基于以上分析，在保持幅度目标值不变的情况下，不断调节锁相环输出信号的补偿相位，观察幅度控制力的变化，当幅度控制力取得极小值时对应的补偿相位即为实际锁相误差的大小。

3 仿真及实验验证

3.1 锁相误差对零偏的影响验证

基于力平衡模式控制系统模型，建立Simulink 仿真模型，软件版本为R2015b。仿真参数如下：仿真步长 1/320000 s，谐振子本征谐振频率：ωd=6500 2π(rad/s)，谐振子有效质量m x=my=2.2(g)，Q=7000000，振幅Ax=8(μm)，最大阻尼轴与最小阻尼轴的Q值相差20%，阻尼轴方位角为8 °电角度，频差0.003 Hz，频率轴方位角为10 °电角度，进动因子K=0.277，仿真模型电路各环节均用增益代替，即不存在锁相误差以外的相移。

为验证存在锁相误差时，谐振频率和力平衡控制力是否会发生变化，进行了施加方波型锁相误差的仿真，如图5 所示。

图5 存在锁相误差时x 方向谐振频率和力平衡控制量随时间的变化Fig.5 The change of resonant frequency in x direction and force balance control amount with time when phase-locking error exists

采集到x方向信号谐振频率并对其做0.1 s 平滑，当锁相环存在锁相误差时，幅度环路跟踪信号的谐振频率变化基本不可见，均值为6499.99987 Hz，峰峰值不超过0.06 mHz。输入角速度为0，当锁相误差改变时，力平衡控制量发生了明显的跳变，即零偏发生了明显的跳变。验证了零偏产生了与锁相误差有关的漂移，该项零偏与锁相误差变化一致。

基于现有实验室平台，进行了锁相误差影响的实验验证。实验前使用转台对陀螺的标度因数进行了测试，并使用陀螺激振后开环检测的方式估测了陀螺频差约为0.003 Hz。实验中保持陀螺静止，保证环境温度不变，陀螺零位不受其他因素影响而改变。

在FPGA 软件的调制相位处添加“锁相误差”并设定其从-4 °～4 °梯度增加，每1 min 变化一个数值，待控制量稳定后记录力平衡控制量的大小，除以标度因数，得到零偏随时间的变化如图6 所示。

图6 锁相误差梯度增加时零偏随时间的变化Fig.6 The change of bias with time as the gradients of phaselocking error increase

可见，随着锁相误差随着时间梯度增加，零偏也随着时间梯度增加，锁相误差对零偏有较大的影响。

3.2 常值锁相误差的校准方案验证

为验证所提出的基于幅度控制力极小值的锁相误差校准方法的有效性，进行了实验验证。实验条件与3.1 节一致。改变调制相位处的补偿相位，并记录稳定时的幅度控制量大小，如图7 所示。

图7 幅度控制量随补偿相位的变化关系Fig.7 The relationship between amplitude control amount and compensate phase

对幅度控制量-补偿相位曲线使用余弦函数拟合，如图7 中蓝色曲线所示，曲线在2.7 °取得极小值，即认为实际锁相误差约为2.7 °。在目前的噪声水平下，锁相误差校准精度约为±0.5 °。

锁相误差校准前后零偏的变化如图8 所示，从150 °/h 减小到了68.46 °/h，减小了约54%，验证了校准方法的有效性。对照实验前对陀螺频差约为0.003 Hz 的估算，变化率与1.2 节的理论分析结果基本一致。

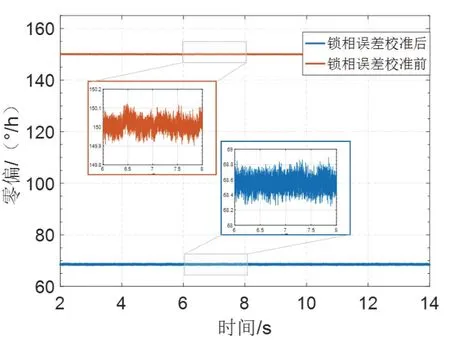
图8 锁相误差校准前后的零偏Fig.8 bias before and after phase-lock error calibration

4 结论

本文对锁相环相位误差对半球谐振陀螺零偏的影响进行了理论分析和验证。对于两件套结构的半球谐振陀螺，当存在锁相环锁相误差时，施加在同一电极上的力平衡控制力和正交控制力会发生耦合，导致零偏出现与锁相误差和频差相关的偏移项，当频差为0.001 Hz 时，零偏变化10.8704 °/h/°。提出了基于幅度控制量极小值的校准方法，实验结果表明，校准后零偏减小了54%，验证了校准方法的有效性。

本文主要研究锁相误差的影响，实际上结论可以推广到y 轴驱动电路的相移，得到类似的结论。本文提出的校准方法也可推广用于锁相误差的实时校准，在驱动端对调制相位进行实时补偿，从而在锁相误差随时间变化时，提升零偏稳定性。