涡轮盘模锻过程中微观组织演变的模拟分析*

2022-12-16刘延星李润华柯志江

航空制造技术 2022年20期

刘延星，李润华，柯志江

（东莞理工学院，东莞 523808）

涡轮盘是航空发动机的关键零件，其高品质制造技术是制约我国航空发动机研制的核心难题之一[1]。高温、高转速及高温度梯度等极端服役环境，对涡轮盘的高温性能提出了极高的要求。涡轮盘的高温性能主要依赖于其微观组织，因此，全面掌握涡轮盘在模锻过程中的微观组织演变规律及机理，对获得高品质航空发动机涡轮盘具有非常重要的意义[2]。

微观组织模拟可以预测涡轮盘的微观组织演变，同时降低工艺优化的成本，节省工艺优化时间。因此，涡轮盘热加工过程中的微观组织模拟得到了国内外的广泛关注。Yukawa等[3]采用遗传算法优化了适用于大型镍基高温合金锻件微观组织预测的再结晶模型。李林翰等[4]模拟了GH4738涡轮盘的模锻过程，分析了平均晶粒尺寸、变形温度等变量的演变规律。KRÄMER等[5]采用有限元法，实现了IN718涡轮盘镦粗、模锻以及热处理等全流程的力学性能及微观组织模拟。Cha等[6]采用有限元法模拟了Waspaloy涡轮盘半封闭式模锻过程，并设计了相应的模具及模锻工艺。尽管众多学者对涡轮盘微观组织预测开展了大量研究，但有关强时变工况条件下微观组织演变的研究却鲜有报道。涡轮盘微观组织通常对变形工艺参数极为敏感，而在涡轮盘模锻过程中，变形工艺参数如变形温度、应变速率等，具有非常强的时变特性，特别是应变速率，在模锻过程中，锻件内部各处的应变速率值甚至会出现急剧的上升和降低。应变速率突变可能会导致涡轮盘微观组织出现异于常规的演变规律，因此，本文采用有限元方法，对涡轮盘模锻过程中的微观组织演变进行模拟，重点分析应变速率突变对微观组织演变的影响及其抵消方法。

1 材料模型

涡轮盘材料选用GH4169合金，此合金耐高温、抗腐蚀、抗氧化，并具有较强的抗蠕变和抗疲劳性能，在航空航天领域中应用广泛，是航空发动机涡轮盘的典型用材。在模拟GH4169合金涡轮盘模锻过程之前，首先需要嵌入GH4169合金的材料模型，包括应力–应变模型、动态再结晶模型以及亚动态再结晶模型等。

在数值模拟中，需要基于材料的应力–应变模型来计算涡轮盘模锻过程的应变、应力等宏观变量的分布和演变。GH4169合金的应力应变本构方程[7]为

式中，ε为应变；T为变形温度；ε.为应变速率；σ为应力；σrec为不考虑动态再结晶软化作用时的应力；σsat为饱和应力；σss为稳态应力；σp为峰值应力；σ0为屈服应力；εc为动态再结晶开启时的临界应变；εp为峰值应力所对应的应变；Z为Zener-Hollomon参数；R为大气常数；Kd和ω为材料系数。

由式（1）计算出GH4169合金的应力数据，并输入至有限元软件中。

GH4169合金在热变形过程中的微观组织演变十分复杂。在变形过程中，通常会发生加工硬化、动态回复、动态再结晶等，在道次间则可能发生静态回复、静态或亚动态再结晶等。GH4169合金是一种低层错能材料，其动态再结晶行为主要包括动态再结晶形核和动态再结晶晶核长大两个部分[8]。在高温变形过程中，当变形达到临界应变εcr时，动态再结晶首先在晶界上开始形核；随着变形的继续，动态再结晶晶核逐渐长大，同时，又有新的动态再结晶形核出现；初始晶粒组织被动态再结晶形核和晶粒长大完全吞噬后，演变为完全动态再结晶晶粒组织。GH4169合金的动态再结晶模型[9]为

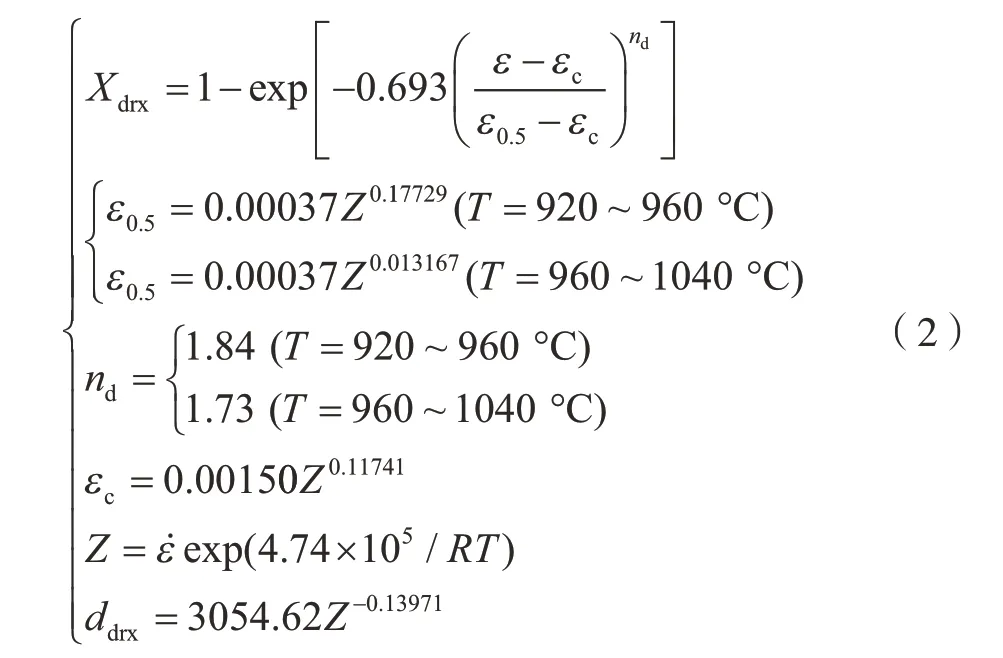
式中，Xdrx为动态再结晶百分数；ε0.5为动态再结晶百分数为50%时所对应的应变；ddrx为动态再结晶晶粒尺寸；nd为材料系数。

通常，当变形程度超过临界应变时，材料内部发生动态再结晶，生成大量动态再结晶晶粒。若停止变形，并继续保温，动态再结晶晶粒会在晶界驱动力的作用下继续长大，这种现象即为亚动态再结晶。GH4169合金的亚动态再结晶模型[10]为

式中，Xmdrx为亚动态再结晶百分数；t为保温时间；t0.5为亚动态再结晶百分数达到50%时所对应的时间；d0为初始晶粒尺寸；dmdrx为亚动态再结晶晶粒尺寸。

2 有限元模型

为了直观地反映应变速率突变对微观组织的影响，首先进行了圆柱试样压缩模拟，随后进行了单道次及多道次涡轮盘模锻过程的模拟。上述模拟均在商用有限元软件DEFORM-2D V11.0中展开，材料为GH4169合金，初始晶粒尺寸为75 μm，具体模型如2.1和2.2节所述。

2.1 圆柱试样压缩有限元模型

图1所示为圆柱试样压缩的有限元模型，在下压量为3 mm时，应变速率由初始值0.001 s–1突变为0.02 s–1，并保持不变直至压缩结束。变形温度为990 ℃，圆柱试样尺寸为Φ8 mm×12 mm，采用四边形单元，对圆柱试样及模具进行网格划分，网格数量均为1000个。为了减少变形不均匀性的影响，圆柱试样与上下模具之间的摩擦系数设置为0。

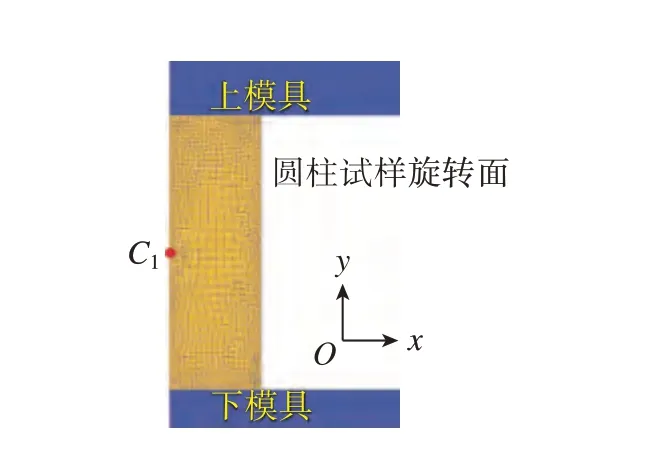
图1 圆柱试样旋转面有限元模型Fig.1 Finite element model of cylindrical sample

2.2 涡轮盘模锻过程的有限元模型

陈小敏[11]采用正交试验对某型发动机一级涡轮盘锻件的坯料形状尺寸进行了优化，图2所示为该涡轮盘锻件图以及优化后的涡轮盘坯料尺寸。基于上述涡轮盘尺寸，分别对涡轮盘单道次及多道次模锻过程进行了模拟。图3所示为涡轮盘模锻成形的有限元模型，采用四边形单元对模具及坯料进行网格划分，其中，模具网格数为4000个，坯料网格数为10000个。模具与坯料之间的剪切摩擦系数为0.3，传热系数为5 N/（s·mm·K），与环境的对流传热系数为0.02 N/（s·mm·K）。

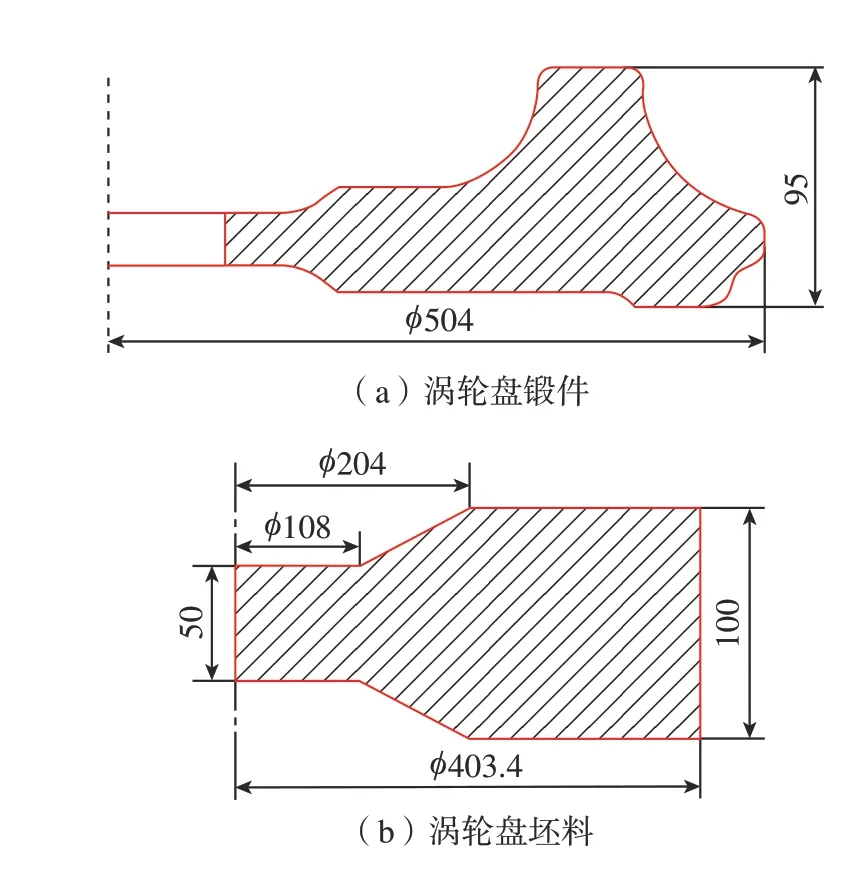
图2 涡轮盘尺寸图（mm）[11]Fig.2 Dimensions of turbine disk (mm)[11]

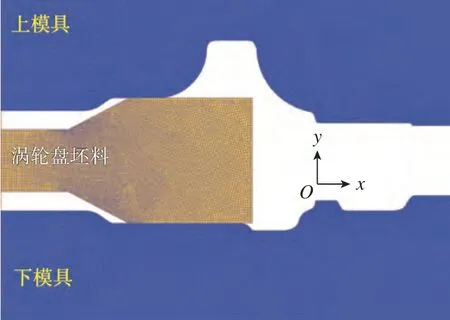
图3 涡轮盘模锻有限元模型Fig.3 Finite element model of turbine disk forging

3 结果与讨论

3.1 圆柱试样

采用图1所示有限元模型模拟了应变速率突增条件下圆柱试样的微观组织演变。从模拟结果中提取了C1点处的应变速率、动态再结晶百分数以及平均晶粒尺寸等数据，具体结果如图4所示（其中实线为应变速率突增条件下的模拟结果，虚线为恒定应变速率条件下的模拟结果）。由图4（a）可知，在模拟过程中，当下压量达到3 mm时，应变速率由初始值0.001 s–1突变为0.02 s–1。变形速率的突增对动态再结晶百分数和平均晶粒尺寸的有限元模拟结果具有明显的影响，如图4（b）和（c）所示。从图4（b）可以发现，此时，点C1处尚未达到完全动态再结晶。在应变速率突增后，点C1处动态再结晶百分数和平均晶粒尺寸的变化曲线均先出现了一段水平段。在下压量达到3.6 mm后，开始逐渐向恒定应变速率的0.02 s–1模拟结果靠近。

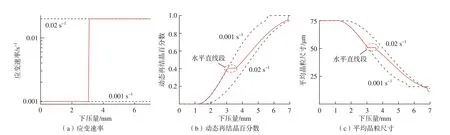
图4 应变速率、动态再结晶百分数以及平均晶粒尺寸随下压量的演变Fig.4 Evolutions of strain rate, fraction of dynamic recrystallization and average grain size with stroke

动态再结晶百分数和平均晶粒尺寸随下压量的变化曲线，在应变速率突增后均出现了一段水平段，即动态再结晶百分数和平均晶粒尺寸在应变速率突增后的一段变形区间内保持不变，动态再结晶发生了暂停。暂停区间对应的下压量范围为3～3.6 mm。为了进一步分析此水平段产生的原因，从模拟结果中，提取了图1中C1点处的应变、临界应变、流动应力以及变形温度等数据，具体结果如图5所示。由图5（a）可知，随着下压量的增大，应变不断累积；应变速率突增后，临界应变由初始的0.13突增至0.18，临界应变升高约0.05。应变速率突增时，对应的应变为0.29，应变累积0.05后，应变增大至0.34，此时所对应的下压量为3.6 mm，动态再结晶暂停区间终止时的下压量也是3.6 mm。即应变速率突增后临界应变有所升高，当应变在应变速率突变后的累积量小于临界应变的升高值时，动态再结晶暂停；当累积量达到临界应变的升高值后，动态再结晶再次开启。因此，这种动态再结晶暂停行为是再结晶开启准则的突增导致的。应变速率突增后，动态再结晶开启准则相应发生改变，动态再结晶发生暂停直至动态再结晶准则再次得到满足。

然而，动态再结晶其实是在位错密度差等能量差的驱动下进行的，即使动态再结晶开启准则发生了突增，新的动态再结晶晶粒减少，但位错密度差等能量差仍然是存在的，原动态再结晶晶粒将继续长大。即动态再结晶仍将继续，不过由于形核作用减弱，导致动态再结晶速度有所减缓。这种由应变速率突增导致的动态再结晶减缓，与亚动态再结晶十分相似，均为形核不明显，动态再结晶晶粒显著长大。因此，此过程可以称为“伪亚动态再结晶”[12]。两者的区别在于伪亚动态再结晶发生在变形过程中，而亚动态再结晶发生在静态保温过程中。同时，尽管应变速率突增条件下的有限元模拟结果不够全面，但足以表明伪亚动态再结晶会延缓动态再结晶过程。因此，在实际热加工过程中，应尽量避免伪亚动态再结晶。

流动应力随下压量的演变如图5（b）所示。应变速率突增后，流动应力急剧升高，升高后的应力值略大于相应恒定应变速率下的值，但随后的演变规律与其一致，均随着下压量的增加而逐渐降低。图5（c）所示为变形温度随下压量的演变。可知，应变速率突增后，变形温度逐渐升高，并向相应恒定应变速率下的变形温度值靠拢。在行程结束时，变形温度仍然低于相应恒定应变速率下的变形温度。因此，图5（b）中突变后的流动应力之所以会略高于相应恒定应变速率下的流动应力，是因为突变后的变形温度略低于相应恒定应变速率下的变形温度。

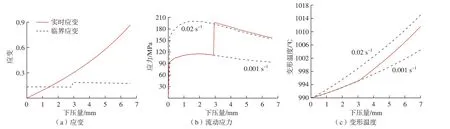
图5 应变、临界应变、流动应力以及变形温度随下压量的演变Fig.5 Evolutions of strain, critical strain, flow stress and deformation temperature with stroke

3.2 涡轮盘模锻

3.1节的圆柱试样压缩模拟结果表明，应尽量避免应变速率突变，防止诱发亚动态再结晶，降低动态再结晶速度。本节将从这一角度出发，分析如何提高涡轮盘关键点处的再结晶程度。

GH4169合金涡轮盘单道次恒定下压速度模锻工艺信息表，如表1所示。在涡轮盘模锻成形的宏观有限元模拟中，模锻温度为990 ℃，上模具下压速度为1.05 mm/s。其中，模锻温度位于涡轮盘常用模锻温度范围950～1010 ℃内，上模具下压速度在模拟过程中保持恒定不变，对应的应变速率范围为0.001～0.01 s–1。模锻结束时，涡轮盘锻件的等效应变云图以及动态再结晶百分数云图如图6所示。由图6（a）可以发现，锻件内部的等效应变分布存在3个局部最小区域，分别如字母A～C所示。对应动态再结晶百分数云图也显示，此3个区域的动态再结晶程度较低。

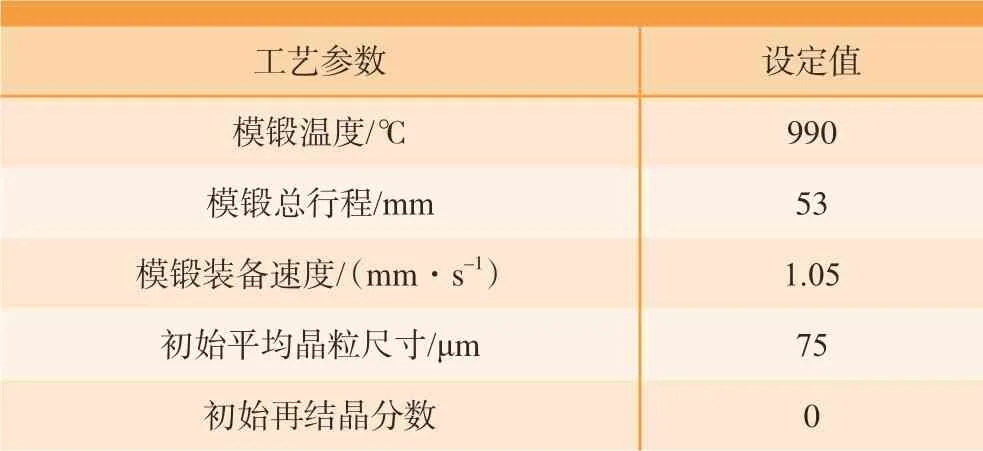
表1 单道次恒定下压速度模锻工艺信息表Table 1 Parameters for single pass forging under constant moving velocity

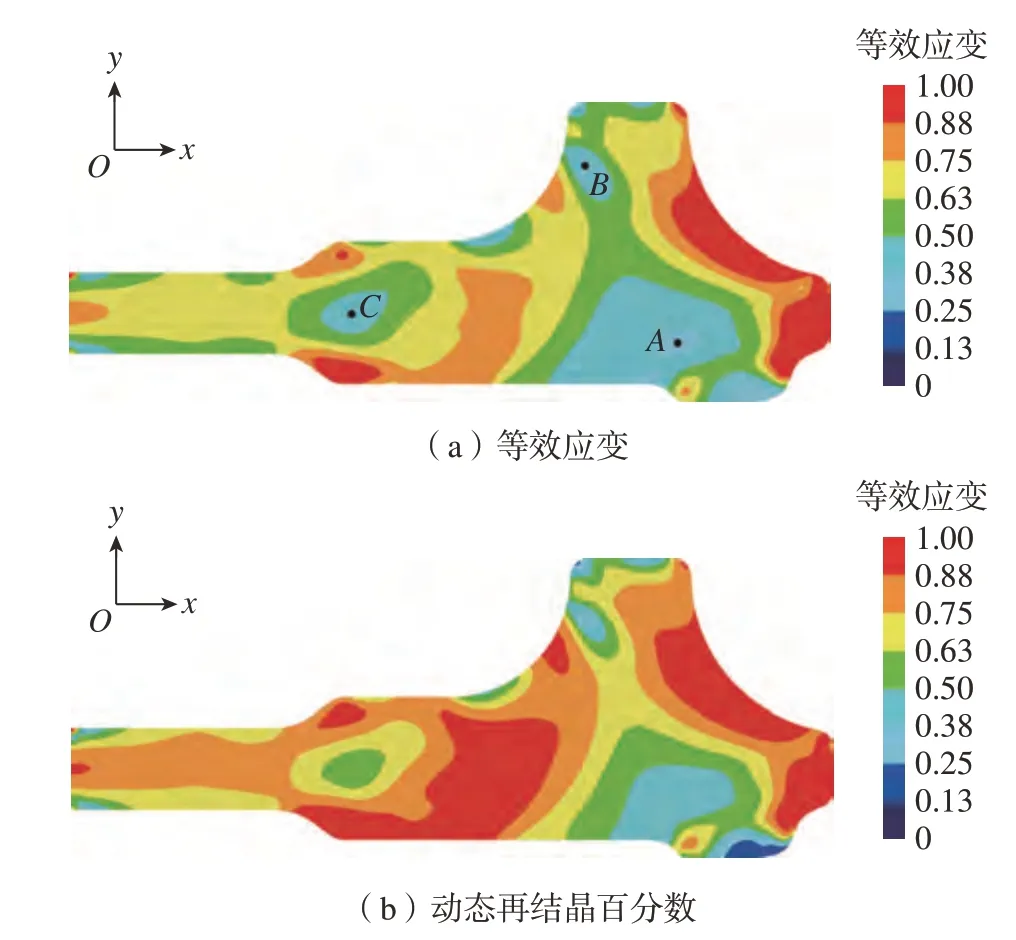
图6 模锻结束后涡轮盘云图Fig.6 Contour plots of turbine disk at the end of forging

在区域A～C中，涡轮盘轮芯附近区域比较容易满足晶粒组织目标要求，轮缘区域较难达到晶粒组织目标要求。但是，B区域位于涡轮盘轮缘的外侧，即使未能达到晶粒组织目标要求，也可在涡轮盘后期的机加工中进行切除。A区域位于涡轮盘轮缘内部，此处晶粒组织一旦未达到目标要求，可能直接导致整个涡轮盘锻件报废。因此，在接下来对涡轮盘单道次和多道次模锻过程的研究中，将以A点作为关键点，探讨如何提高其再结晶程度。

3.2.1 单道次模拟

图7所示为在恒定下压速度下，关键点A处应变速率及动态再结晶百分数的模拟结果。由应变速率曲线可以发现，应变速率具有较强的时变性。应变速率在模锻行程为42 mm时，从0.009 s–1迅速升高至0.025 s–1；随后在模锻行程为51 mm时，从0.007 s–1迅速升高至0.015 s–1。由动态再结晶百分数曲线可知，动态再结晶速度较慢，在行程结束后，动态再结晶百分数仅为0.4。同时，在应变速率突变附近，动态再结晶百分数曲线上并未出现明显的伪亚动态再结晶现象。这可能是有限元模拟方法在模拟强时变工况条件时的精度不足所致，后续可通过元胞自动机法、相场法等更全面的微观组织模拟方法加以验证。

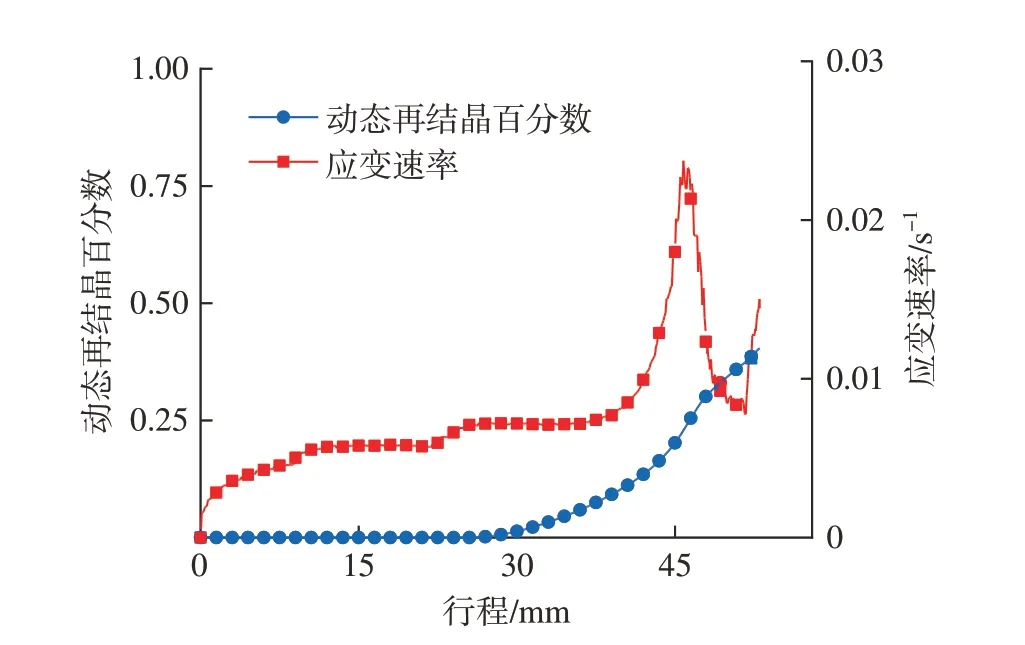
图7 恒定下压速度下关键点A处的应变速率及动态再结晶百分数Fig.7 Strain rate and fraction of dynamic recrystallization at key point A under constant moving velocity

由于圆柱试样模拟结果已经表明应变速率突增会降低动态再结晶速度，因此接下来尝试调整模锻行程42 mm后的下压速度，避免出现急剧的应变速率突增，以提高关键点A处的动态再结晶程度。假设下压速度与应变速率之间的比值仅为行程的函数，基于图7中的应变速率数据，以应变速率0.01 s–1和0.005 s–1为目标值，计算得到了相应的下压速度值，如图8所示（其中，变下压速度1和变下压速度2分别对应目标值为0.01 s–1和0.005 s–1时的下压速度）。

将上模具的下压速度分别设置为图8所示的变下压速度1和变下压速度2，对应的应变速率和动态再结晶百分数模拟结果分别如图9所示。由图9（a）可知，在变下压速度1和变下压速度2的条件下，关键点A处在行程42 mm后的应变速率均近似相等，分别约为0.01 s–1和0.005 s–1，与模拟前的计划目标值相等，表明前述假设是可靠的。从图9（b）可以发现，行程结束后，变下压速度1和变下压速度2的条件下的动态再结晶百分数均有所提高，分别为0.42和0.45。因此，可以通过避免应变速率突增来提高关键点处的动态再结晶程度。

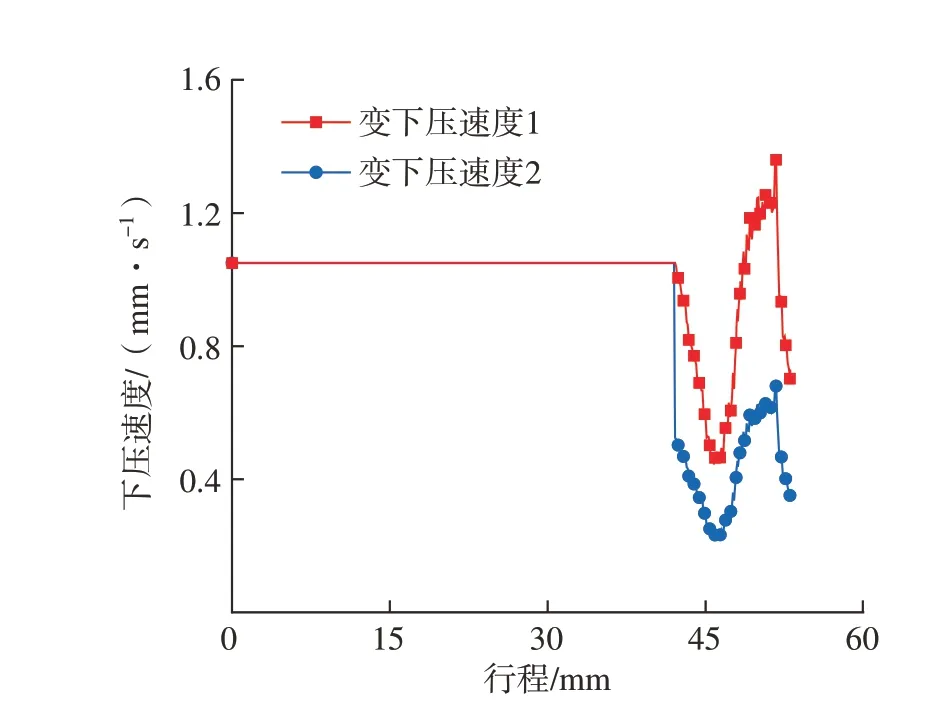
图8 上模具的变下压速度值Fig.8 Varying moving velocity for top die

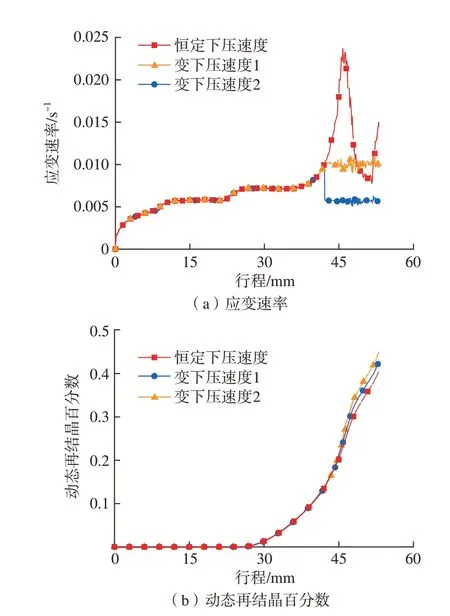
图9 变下压速度条件下关键点A的模拟结果Fig.9 Results at key point A under varying moving velocity

3.2.2 多道次模拟

除可通过避免应变速率突增来提高关键点再结晶程度外，道次间的保温操作也可以在亚动态再结晶的作用下改善关键点的再结晶状态[13]。图7显示，在恒定下压速度下，应变速率将在行程为42 mm和51 mm后发生突变。为了抵消后续应变速率突增对再结晶速度的阻碍作用，在行程为42 mm和51 mm处，执行保温操作，保温时间为30 s。具体的多道次模锻工艺信息如表2所示。

表2 多道次模锻工艺信息表Table 2 Parameters for multi-pass forging

图10所示为多道次模锻过程中，关键点A处的再结晶百分数以及平均晶粒尺寸的演变。可知，在行程为42 mm和51 mm时，关键点A处的再结晶百分数持续升高，平均晶粒尺寸不断降低。这是因为保温过程中，亚动态再结晶开启，再结晶晶粒在位错密度差的驱使下，持续吞噬应变硬化的原始晶粒。经道次间隔保温处理，在行程结束后，关键点处的再结晶程度已经接近完全，再结晶百分数约为0.92，平均晶粒尺寸细化至27 μm，这表明多道次模锻成形有助于提高模锻结束时坯料的再结晶程度。