考虑电压电流约束的感应电机容错运行对比研究

2022-12-16孙凯陈伟斌翟晓卉

电源学报 2022年6期

孙凯，陈伟斌，翟晓卉

（国网山东省电力公司营销服务中心（计量中心），济南 250003）

感应电机作为诸如电动汽车、纺织、农具、家用电器、钢铁和造纸等工业场景中广泛使用的动力设备，其驱动系统的可靠性日益重要[1-2]。因此，为了提高可靠性，对感应电机容错控制开展了众多研究以实现其不间断运行[3-5]。容错控制研究包括：故障检测、故障缓解和故障容错运行。首先，故障检测的实现通常通过将处理后采样信号与设置阈值进行比较来定位故障和诊断故障类型[6-7]。然后检测到故障后，考虑采取补救措施来减轻故障，如文献[8-10]中描述，这涉及到驱动器的硬件重构。在完成系统重新配置后，配合所设计的容错控制算法，可最终实现故障后电机驱动系统良好的运行性能。尽管在容错设计中使用多相电机的趋势仍不断增加[11-12]，同时还有通过使用开放式绕组电机实现容错运行的实例[13]，但这些方案需要更多的元件，同时系统复杂度更高，同时考虑到三相电机仍在工业市场上占主导地位，故常规三相电机容错研究仍然值得关注。尽管可使用绕组三角形连接的电机实现容错驱动[14]，但大多数容错控制研究仍集中于绕组星形连接的三相电机，而驱动器为三桥臂两电平逆变器。

根据故障类型和定位，以及相关文献[15-20]中描述，可绘出4 种主要的三相感应电机驱动系统容错配置。容错配置主要是通过激活一些连接以重构驱动器，并通过合并辅助设备来实现故障容错运行。除了拓扑重构外，控制器也需对应进行调整。

文献[21-25]对三相交流电机驱动系统的容错方案进行了论述和对比分析，并确定了各种故障类型的覆盖范围、容错运行成本和适用控制算法等。但在这些分析中，仅由逆变器的电压和电流限制来计算故障容错运行时的输出功率，并未考虑励磁电流的影响，而感应电机中这是必须要考虑的，因此也无法确定故障容错运行下输出转矩限制。同时，由于故障后电机所需电压和逆变器可提供的电压都与正常模式下不同，而是与系统重构类型和工作条件相关，从而本文对此进行详细分析，确定容错运行模式下电机的最大转速，进而确定故障后最大输出功率。因此本文的主要贡献在于分析系统层面电流和电压限制对三相感应电机驱动系统故障容错运行能力的综合影响，并进行实验验证。

1 三相感应电机方程

下面将从正常状态下三相感应电机数学模型切入，推导出只有两相正常时的电机方程，从而获取故障模式下的电压和电流关系式。常规三相星形绕组感应电机驱动系统如图1 所示。

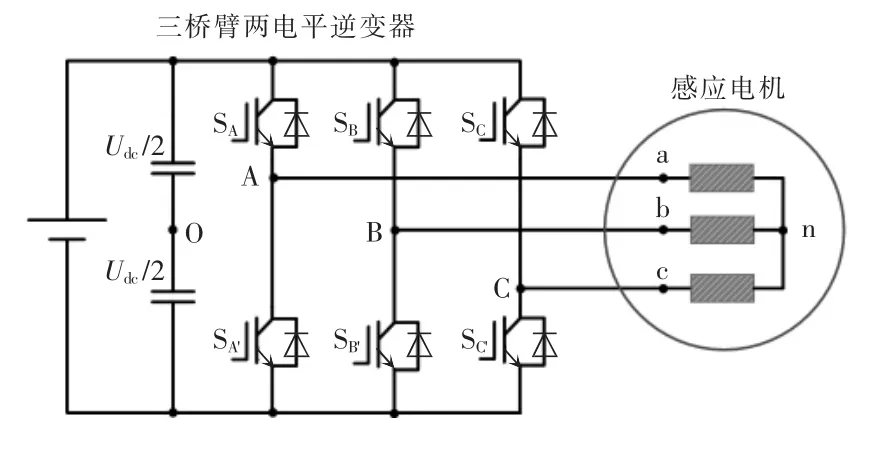
图1 常规三相星形绕组感应电机驱动系统Fig.1 Conventional three-phase Wye-configuration winding induction motor drive system

三相感应电机驱动系统故障容错拓扑配置如图2 所示。图2（a）和（c）中的故障相保持开路并以两相模式运行，此时需将直流母线中点[15]或辅助桥臂中点连接至电机绕组中性点[16-17]以实现电流路径。而图2（b）和（d）则将故障相重新连接到逆变器，即将故障隔离在逆变器侧，电机仍保持三相运行。故障相电机端子可连接至直流母线中点[18-19]或辅助桥臂[20]。

图2 三相感应电机驱动系统故障容错拓扑配置Fig.2 Fault-tolerant topological configuration of threephase induction motor drive system

1.1 非故障时的感应电机数学模型

abc 坐标系下三相感应电机电压方程为

式中：u、i 和λ 分别代表为电压、电流和磁通矢量；下标“s”和“r”分别代表定子和转子；rs、rr分别为定子电阻和转子电阻；p为微分算子。

为了便于控制，将电机方程在αβ0 坐标系中表示，具体可通过应用Clarke变换获得

进一步进行Park变换得到dq0 旋转坐标系下的电机方程为

式中，ωs为同步角速度。使用等幅度变换，则三相正常时的电机相电压和相电流幅值应是对应dq 轴分量的矢量和幅值。

根据图2 所示，故障重构后3LFPCM 配置和4LFPCAL 配置依然具有三相运行条件，故电机方程仍与三相正常时相同，即如式（1）～式（4）所定义。但重构会导致逆变器电压降低，也会带来一些限制，稍后将进行讨论。

1.2 故障后两相运行时感应电机数学模型

对于故障重构后3LNCM 配置和4LNCAL 配置，感应电机仅以两相运行，而感应电机两相运行时气隙磁场非圆形旋转磁场，负序磁场将产生一些不利影响，如转矩脉动等。因此，不能直接使用常规方程，有关三相电机在两相模式下的容错控制以及转矩脉动抑制研究已较为成熟[17-18，26-27]，在此不再赘述，但不管采用何种控制，其结果都需要将余下正常两相的相电流适当控制以使电机保持基频旋转磁动势，即迫使感应电机两相运行时气隙磁场呈圆形。换言之，容错控制的关键还在于对电机磁通的控制，即式（1）中的λabcs。实际上，定子每相磁通包含两部分，即由定子电流产生的定子磁通λabcs（is）和转子电流产生的定子磁通λabcs（ir）。

但仅需要考虑λabcs（is），因为鼠笼式感应电机只能直接控制定子电流。适当的容错控制将确保故障后定子磁通与正常情况下相同，从而使转子电流和与转子电流相关的磁通项保持不变。

基于叠加原理，式（5）中定子电流产生的磁通项可扩展写为

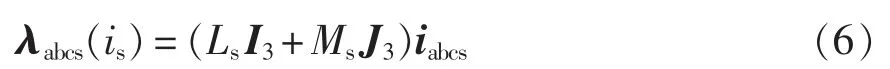
式中，I3和J3分别是单位矩阵和元素全为1的3 阶矩阵。定子电感Ls和Ms为

式中，Lls和Lms分别为定子漏感和励磁电感。通过将等幅值Clarke变换应用于式（6），可获得定子磁通αβ 轴分量与定子电流的函数关系为

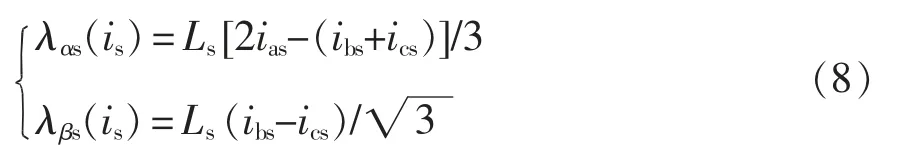
不失一般性，设a 相故障开路且电流变为0，则式（8）改写为

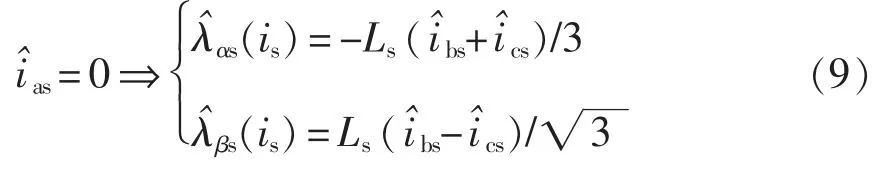
式中，上标“^”代表故障后的变量。由于容错控制的目的是使定子磁通保持原正常状态，故式（9）应等于式（8），从而推导得

式（10）表明，为实现容错运行，故障后b 相和c相电流将是对应正常电流的3倍，并且彼此之间相移60°。式（10）清楚地显示了以正常电机定子电流表示的故障电机所需定子电流。

将式（10）代入式（5），故障后电机定子磁通为

将式（10）和式（11）代入式（1），可以用正常的电机变量表示故障后电机定子相电压。

式（12）说明了故障后电机定子相电压等于各自的正常定子相电压减去一个公共电压项，而该公共电压项是图3 中所示的故障相定子端电压uza（漏感和电阻串联端电压）。

图3 故障相等效电路Fig.3 Equivalent circuit in fault phase

图4为基于式（1）的三相正常时电机、以及基于式（12）的故障后电机定子相电压和相电流矢量图，其中虚线矢量显示出了故障前后各个矢量间的差异。

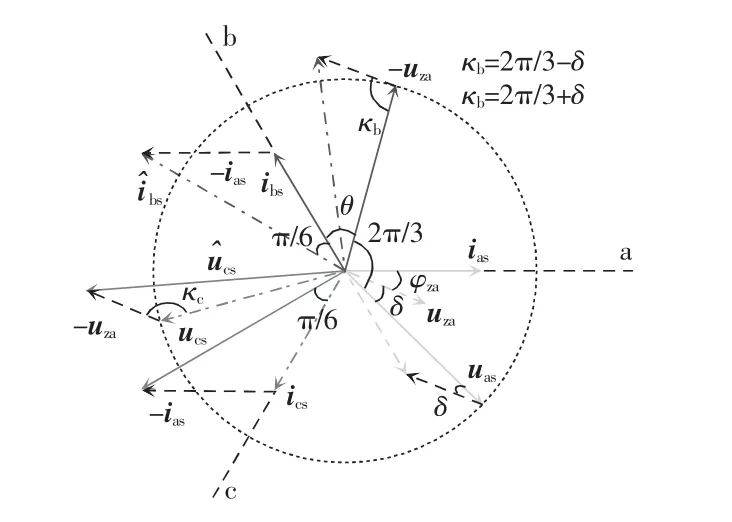
图4 故障前后电机定子电压电流矢量Fig.4 Voltage and current vectors of motor stator before and after fault

由图3 可得，故障相定子端电压uza的幅值和相角为

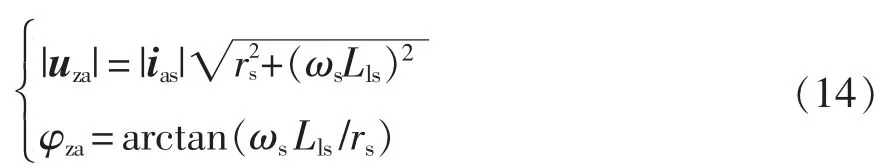
式中，|uza|、φza分别为uza的幅值和相角。从图4 中可看出，故障后b 相和c 相的电压幅值取决于|uza|和φza，以及功率因数角θ。图4 中角度δ 定义为uza的相角φza与功率因数角θ 之差，即

采样转子磁通定向控制，则d 轴与转子磁通矢量对齐，定子电压方程可写成定子电流的函数，并易获得功率因数角，表示为

式中：uds、uqs、ids和iqs为dq 轴定子电压和电流；ζ为定子电流因数；σ为总漏磁系数，二者分别为

由式（16）和式（17），功率因数角θ为

由式（14）～式（18）可计算非故障两相的相电压峰值为

值得注意的是，故障相的相电压幅度可忽略，不需考虑，因为该相已经断路并不再受逆变器的影响。分析式（19），可得出故障容错运行模式下的电机相电压相关的结论为：①容错运行模式下相电压幅值取决于电机参数以及运行工作点；②由于δ 不必为0，所以余下正常两相的电压幅值不必相等；③容错运行模式下的定子线电压幅值与正常时相同。

从推导过程可看出，容错运行模式下的电机相电压取决于电机参数以及由ids、iqs和ωs所定义的工作点。对于给定的ids和iqs，故障后电机可达到的最大转速取决于逆变器可提供的最大电压，这将在下文进行讨论。

2 容错运行模式下的逆变器容量分析

完成对故障后电机相电压的量化分析后，有必要进一步分析容错模式下逆变器的容量，从而明确逆变器是否能在容错运行模式下提供所需电压和电流。就电流而言，可合理地假设逆变器功率开关器件设计为可承受电机的额定相电流，这也意味着在故障容错运行期间必须降额，以确保不超过逆变器电流限值。

从图2 中可看出，无论电机故障相如何连接到逆变器，逆变器的最大桥臂电压和桥臂间电压都是固定的。定义逆变器三相桥臂对直流母线中点的相电压分别为uAO、uBO和uCO，而桥臂间线电压定义为uAB、uBC和uCA，则uAO、uBO和uCO均小于Udc/2，uAB、uBC和uCA均小于Udc。不同系统重构方式下，逆变器输出相电压和线电压对电机定子相电压uan、ubn和ucn，以及线电压uab、ubc和uca产生不同影响。

电机定子相电压非逆变器直接控制，但电机定子线电压则是与逆变器输出线电压直接相关，即其受限于逆变器输出线电压，范围为±Udc。但系统故障重构后，须重新分析逆变器输出电压与电机电压之间的关系。在分析前，对逆变器作如下设定：①故障前后直流母线电压保持不变；②对于3LNCM 和3LFPCM 配置，直流母线包含有可连接中点，即由分离式直流电源组成直流母线；③除附加桥臂外，逆变器桥臂额定电流值应等于电机额定电流；④故障后逆变器顺利完成重新配置，各连接均是可靠的。

2.1 3LNCM 配置

在3LNCM 配置下，系统重构以电机中性点连接至直流母线中点实现，如图2（a）所示。此配置中，非故障定子相“bn”和“cn”上的相电压受逆变器输出相电压uBO和uCO限制，因此范围为±Udc/2，而“bc”上线电压受逆变器输出线电压限制，范围为±Udc，分别表示为

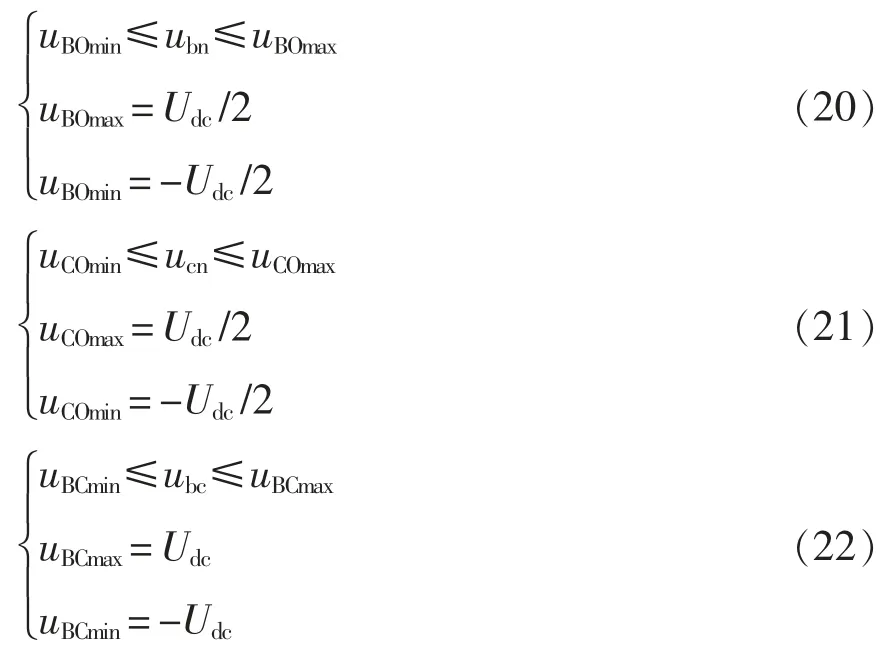
式中：uBOmax、uBOmin分别为uBO的最大值和最小值；uCOmax、uCOmin分别为uCO的最大值和最小值；uBCmax、uBCmin分别为ubc的最大值和最小值。

中性点电流将为额定相电流Ia的3倍，即inO=3Ia，同时该电流必须通过线路“n-O”返回到直流母线中点。故需设置大容值直流电容以保持直流侧中点电压平衡。

2.2 3LFPCM 配置

如图2（b）所示，在3LFPCM 配置下，故障相对应的电机端子直接连接至直流母线中点。“bc”上的线电压仍受逆变器输出线电压限制，范围为±Udc，但由于“a”点直接连接至直流母线中点“O”，因此“ab”和“ca”的线电压范围为±Udc/2，分别表示为

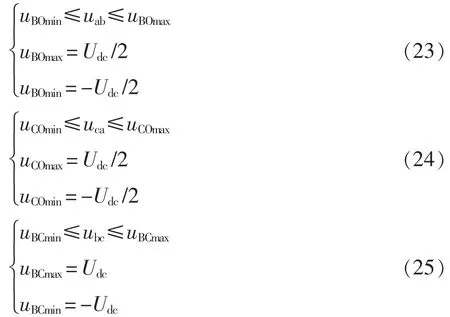
如果直流母线电容器能够容纳a 相交流电流而不考虑中点电压波动，则该配置下逆变器传递至定子相电流的能力与正常驱动时相同，即

2.3 4LNCAL 配置

在4LNCAL 配置下，系统重构以电机中性点连接至逆变器附加桥臂来实现，如图2（c）所示。这意味着中性点电流通过附加桥臂返回至直流侧，即电机的剩余2 个非故障相将由逆变器三条支路控制。“bc”线电压以及“bn”和“cn”相电压均由逆变器输出线电压限制，范围为±Udc，表示为

式中：uBNmax、uBNmin分别为ubn的最大值和最小值；uCNmax、uCNmin分别为ucn的最大值和最小值。

若逆变器附加桥臂电流inN设计为可承受其他三相桥臂额定电流的3倍，则可以将非故障相的电流增加到额定值，即

2.4 4LFPCAL 配置

如图2（d）所示，在4LFPCAL 配置下，故障相由逆变器附加桥臂替代，连接方式恢复至正常图1 所示电机驱动系统拓扑。只要附加桥臂具有与其他桥臂相同的额定电流，则逆变器输出电流就与正常情况下完全相同，此时该重构拓扑可被视为正常运行，后续实验中将不再讨论。

表1 中总结了图2 中所有重构拓扑配置下系统输出电压和电流的边界，其中电压和电流分别相对于直流母线电压和额定电流进行标么化。

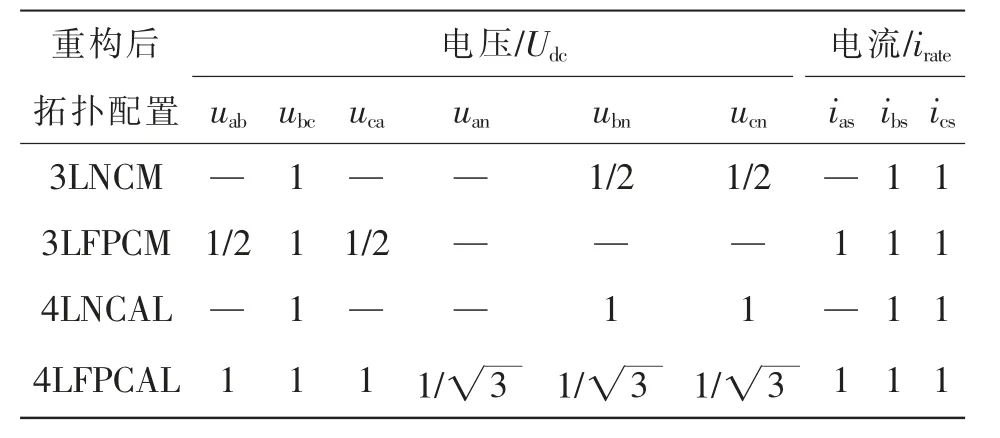
表1 不同配置下的电机电压和电流边界Tab.1 Boundaries of motor voltage and current under different configurations

3 容错控制运行边界分析

通常，感应电机最大输出转矩受电流限制，而最大转速，即输出功率受电压限制。图5 所示为非故障条件下感应电机驱动系统的转矩-功率-转速曲线。图中区域Ⅰ和Ⅱ分别为恒转矩和恒功率区。在满足驱动系统额定电压和额定电流时，额定转速下可以达到最大功率。

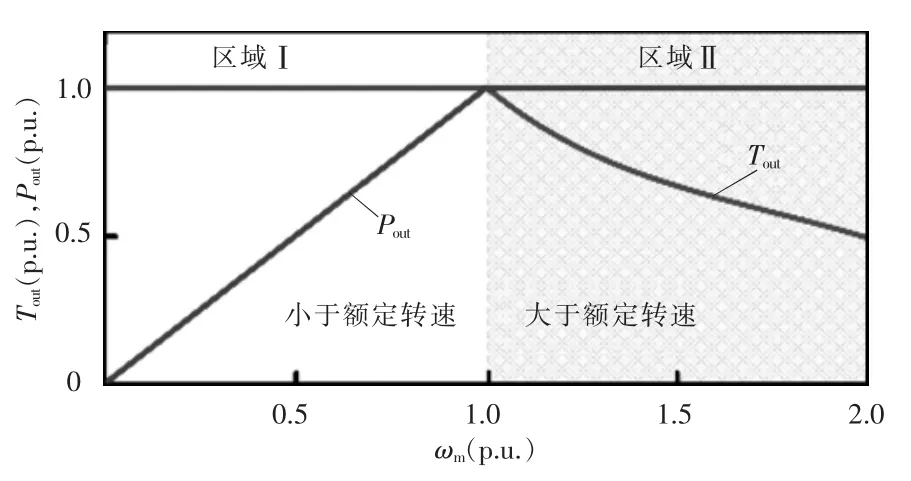
图5 非故障感应电机驱动系统的转矩-功率-转速曲线Fig.5 Torque-power-speed curve of healthy induction motor drive system

但是，由于重构后拓扑配置不同，驱动系统中的电流和电压限制也会有所不同，因此转矩-功率-转速曲线会随表1 中的电压电流限制而有所不同。

对于3LFPCM 和4LFPCAL 配置，容错运行时电机最大相电流等于额定电机相电流，因此d 轴电流ids和q 轴电流iqs可保持额定值。但对于3LNCM和4LNCAL 配置，容错运行时电机相电流的大小由式（10）给出。为了确保不违反相电流限制，需降低容错运行时的ids和iqs，降额系数为，即

值得注意的是，对于不考虑励磁电流的永磁电机，将q 轴电流降额至原来的，也会导致转矩减小到原来的，因此转矩减小与电流降额相对应。但对于感应电机，基于式（31），将dq 轴电流均降额至原来的，会使转矩减小到额定值的因此，对于相同的电流降额，感应电机驱动系统的容错运行输出转矩始终低于永磁电机驱动系统。但基于前述推导，可总结出如下2 个结论：

首先，通过减少ids，则式（4）和式（19）中的电机电压幅值将降低，从而为增加转速提供了额外的空间，转速的增加实际上补偿了低转矩，并增加了容错运行时感应电机的输出功率。

其次，减少ids会影响到有效励磁。在容错运行时，稳态转矩方程为

只要励磁电感Lms保持恒定，式（32）中ids和iqs的减小理论上就将使得输出转矩减小到额定值的1/3。使用转子磁通定向控制时，励磁电感Lms是励磁电流im的函数[26]，而im则是d 轴电流ids的函数。

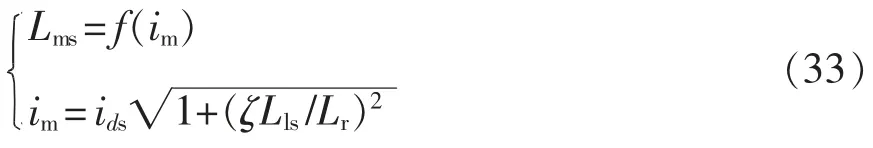
由式（31）和式（33），励磁电流im的减小是与d轴电流ids的减小同步的，随着im的减小，由于磁饱和效应，励磁电感Lms实际上会增加，如图6 所示。这种励磁电感的增加会提高式（32）中的输出转矩，但会减小转速增加的空间。因此，为了准确确定故障容错运行时的电压边界，应根据电机的磁化曲线更新式（16）和式（19）中与Lms相关的项。

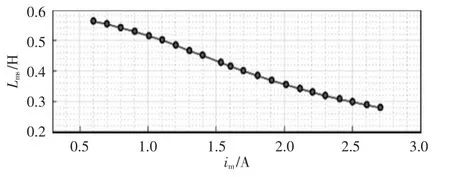
图6 测试感应电机的磁化曲线Fig.6 Magnetization curve of tested induction motor

4 实验验证

为验证前述分析和结论，搭建了图7 所示的感应电机容错控制实验平台，并开展了相关测试。

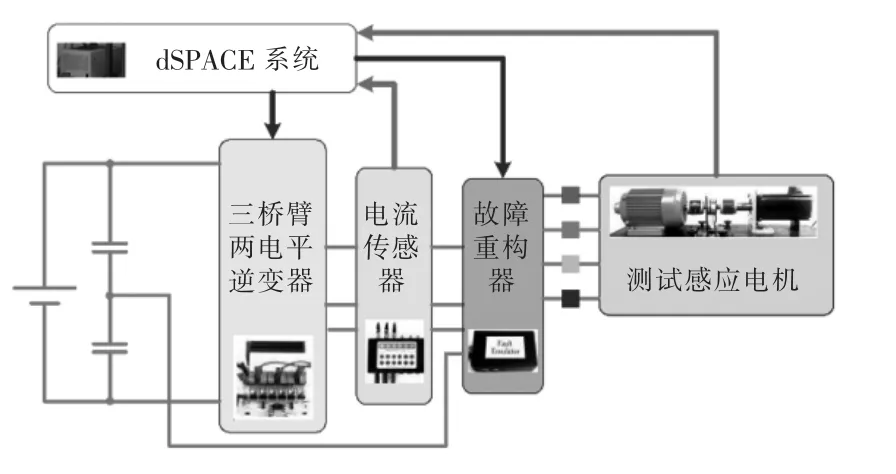
图7 测试平台Fig.7 Test platform

其中测试鼠笼式感应电机主要参数如表2 所示。实验平台中感应电机对拖永磁同步发电机，永磁同步发电机接可变负载，容错控制策略由dSPACE（DS1104）系统实现，开关频率设为5 kHz，同时设置3 个电流传感器和增量式旋转编码器进行电流和转速测量，直流侧电源包含有2 组2 200 μF的电容器，直流母线中点引出用于系统重构。逆变器A相桥臂设置有继电器，通过断开继电器来模拟A 相开路故障，然后根据所需的故障容错拓扑类型进行线路重构，继电器信号被发送到容错控制器，完成从正常运行模式到故障容错运行模式的切换。

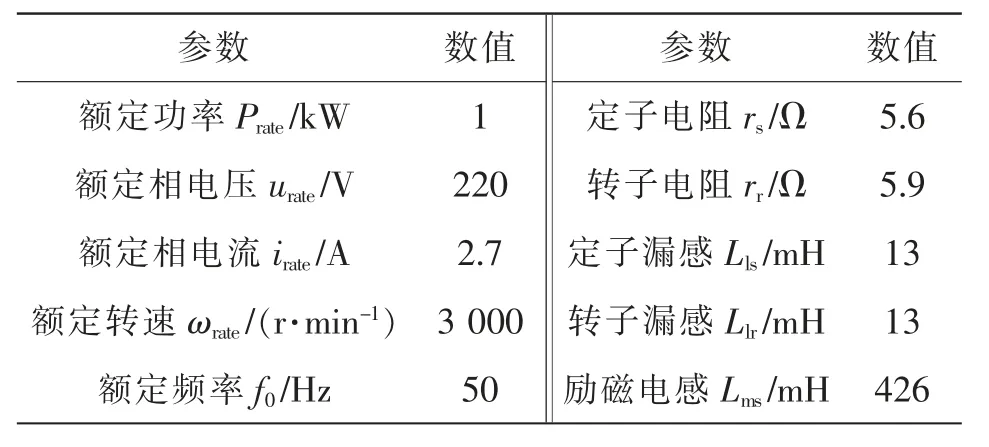
表2 感应电机参数Tab.2 Parameters of induction motor

为了评估感应电机驱动系统运行边界，进行了如下实验操作，将和设置为各自额定值，以便在系统正常运行和故障容错运行模式下，相电流均达到其额定峰值3.81 A。在电流保持在极限值的情况下，将感应电机转速逐渐增加到线性调制区的极限，以使其在电压极限下获得最大转速。在dSPACE 控制界面中获得的正常运行模式和故障容错运行模式实验波形分别如图8 和图9 所示。从测试结果可看出，ids和iqs分别保持在各自的最大参考值，其中3LNCM 配置和4LNACL 配置下ids和iqs只有3LFPCM 配置的而相电流均保持为额定值不变。值得注意的是，尽管使用了大容量分压电容器，但3LNCM 和3LFPCM 配置下的直流母线中点电压存在较大振荡，从而导致ids和iqs的纹波显著增大。

图8 额定负载最大转速下的系统正常运行实验波形Fig.8 Experimental waves of system under normal operation at rated load and maximum rotation speed

图9 额定负载最大转速下的系统故障容错运行实验波形Fig.9 Experimental waves of system under faulttolerant operation at rated load and maximum rotation speed

图10 和图11 分别为正常和故障容错运行模式下不同转速时测得的相电压和线电压，以及基于式（4）、式（16）和式（19）确定的电压随转速变化的理论计算值，当计算值达到限值时即为恒转矩区中最大转速。从图10 中可看出，对于正常运行工况，电机相电压和线电压都在各自限值处达到额定转速3 000 r/min。对于3LNCM 和4LNCAL 配置，电流降额将导致Lms变化，故这2 种配置下的控制算法中均将Lms参数设置为530 mH，而非426 mH。从图11中可看出，3LNCM 配置下，电机相电压将在线电压前达到限值，对应最大转速为3 572 r/min；3LFPCM配置下，线电压uab和uca首先达到限值，对应最大转速为1 440 r/min；4LNCAL 配置下，线电压ubc将先于相电压达到限值，对应最大转速为4 292 r/min。

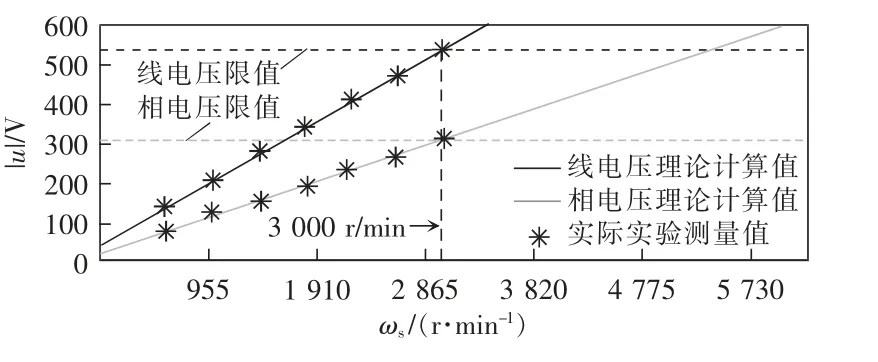
图10 正常运行下电压随转速变化趋势Fig.10 Changing trend of voltage with rotation speed under normal operation

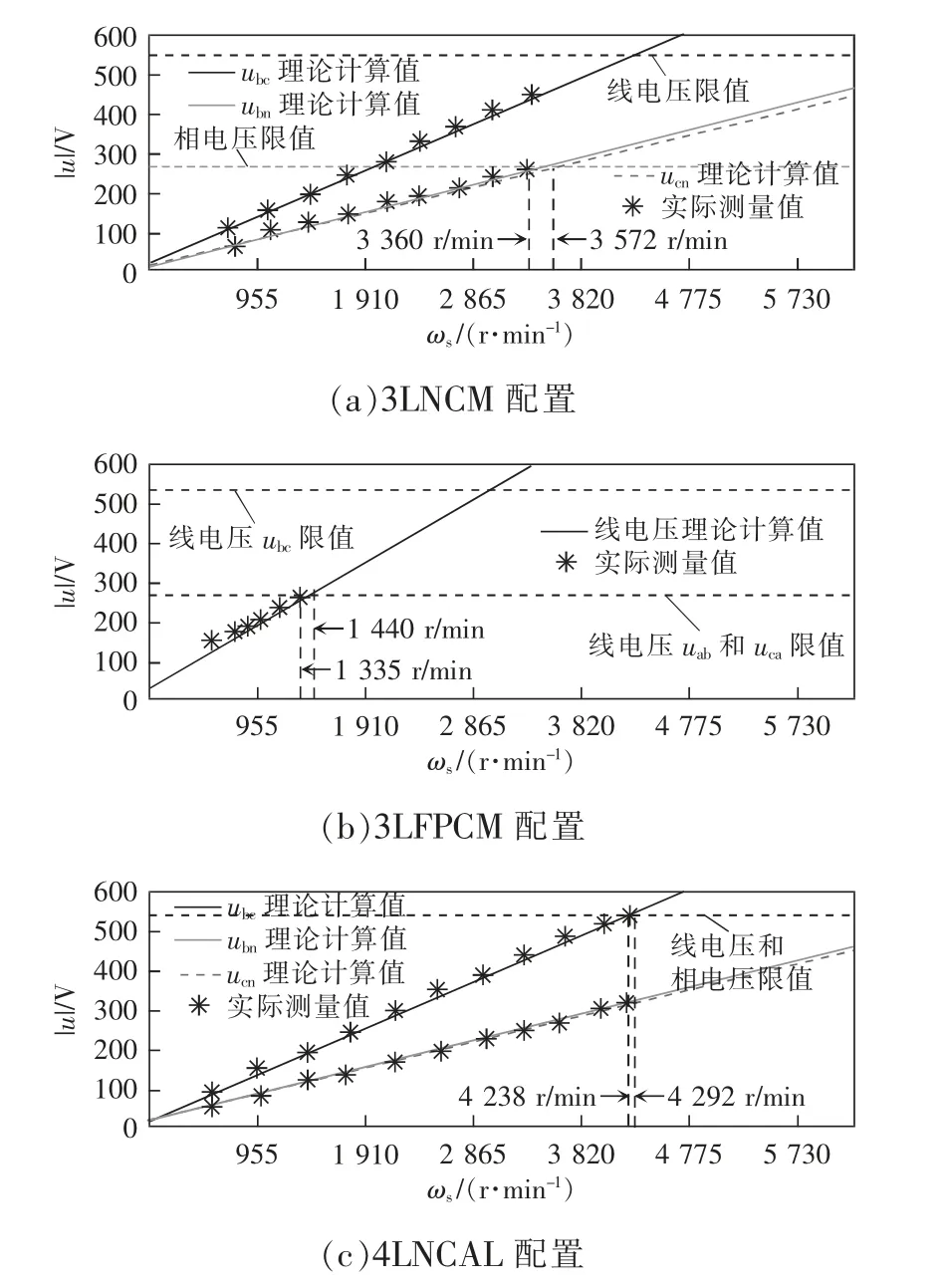
图11 故障容错运行下电压随转速变化趋势Fig.11 Changing trend of voltage with rotation speed under fault-tolerant operation

综上，实验结果验证了理论分析得到运行边界。值得注意的是，对于3LNCM 配置和3LFPCM 配置，由于直流母线中点电压存在波动，实验中能达到的最大转速稍低于理论限值，这也是2 种故障重构拓扑的主要缺点。为了更好地对比分析，根据实验结果，绘出了图12 所示的不同容错配置下的转矩-功率-转速曲线。

图12 故障容错运行时的转矩-功率-转速曲线Fig.12 Torque-power-speed curve under fault-tolerant operation

从图12 中可得到如下结论：

（1）不同电机容错运行模式下转速限值与转矩限值有所不同。对于3LNCM 配置和4LNCAL 配置，即使转矩限值为原来的1/3，恒转矩区理论上也分别扩展了48.7%和75.%。在额定转速以上区域，系统最大输出功率为0.49 p.u.和0.58 p.u.。对于3LPFCM 配置，转矩限值与正常运行时相同，但输出功率仅为0.41 p.u.，这是因为恒转矩区域减少了59%（考虑了直流母线中点电压波动的影响）。

（2）系统容错运行性能受Lms特性影响。首先，由于故障后ids降额而导致Lms增加会在恒转矩区域内增加故障容错运行输出转矩。其次，Lms增加减少了恒转矩区扩展，但最大输出功率不会受太大影响。即图12（a）中3LNCM 配置下的故障容错运行转矩从0.33 p.u.增加到0.42 p.u.，但恒转矩区域的扩展下降至只有15.4%。同理，图12（c）中4LNCAL配置下的故障容错运行转矩也增至0.42 p.u.，但恒转矩区域的扩展下降至只有46.4%。对于这2 种情况，转矩的增加补偿了转速的降低，但无论是否考虑Lms的影响，容错运行最大输出功率都大致保持了相同。