无线传感技术在农村电网运行监测应用的研究

杨怡楠高扬

(1.国网吉林供电公司经济技术研究所，吉林 吉林 132000；2.国网长春供电公司供电服务指挥中心，吉林 长春 130000)

前言

农村电网指的是县级市、区级区域内的城镇、农村、农垦区及林牧区用户供电及以下配电网，农村电网的合理规划和管理能够促进农业生产、人民收入、生活水平的提高。但农村因为其地形因素，居民数量多且分布广，用电负荷分布较为分散，电网铺设输电节点多、输电线路长，若不能合理地制定电网设备建设运维方案就会导致电力系统在建设、检修时的诸多不便，甚至增加较高的运维成本。因此，为探究科学有效的农村电网设备运维检修方案，提出将基于改进混合蛙跳算法的无线传感器网络应用于农村电网建设中，利用概率仿真模型对农村电网覆盖情况进行建模，把农村电网设备巡检覆盖率作为待优化目标函数，通过改进混合蛙跳算法对其进行优化。仿真验证优化后的农村电网设备巡检网络覆盖率更大、节点分布更佳均匀，网络覆盖性能显著提升。

1 无线传感器网络概述

无线传感器网络由许多分布于感知区间内的传感器节点共同构成，其同时具备环境感知、无线通信和数据计算的功能，利用彼此合作把自身感知范围收集的数据信息融合，通过单跳、多跳等模式把采集信息送到汇聚节点[1]。WSN节点通过利用环境信息感知、数据传输和处理的能力，成功把实物和网络联系起来，这种研究角度有效推动世界无线传感科技进步的潮流。

2 改进的混合蛙跳算法

混合蛙跳算法(Shuffled Frog Leaping Algorithm，SFLA)的提出使优化问题的研究更佳便捷，其主要原理是结合了协同搜索的进化方式，通过模拟在池塘中觅食的青蛙群体设计出混合蛙跳算法，在青蛙觅食过程中其会进行思想交流，也映射出优化问题中局部数据交流、全局最优搜索的特点[2]。尽管对混合蛙跳算法的研究已经取得了很大的成果，但是还存在很多的问题需要研究学者进一步研究和改进。

针对初始种群随机生成伴随的解的不均匀分布、移动步长的更新策略有待加强和全局搜索自我学习能力弱等问题，从4个方面对SFLA进行改进，分别是种群初始化、分组、更新策略和淘汰混合过程，进而提出改进的混合蛙跳算法(Improved Shuffled FrogLeaping Algorithm，ISFLA)。

2.1 基于反向差分思想的种群初始化

传统SFLA是通过随机生成的方式产生初始解，完成种群初始化过程，这种方式很简单，但这种随机性却给算法的结果增加了很大程度的不稳定性，若随机解与最优解差距较大，那么收敛速度就过于缓慢，影响算法搜索进度和优化性能。对于这个问题，将反向差分的思想与种群初始化过程中随机生成解的方式做一个融合。

(1)

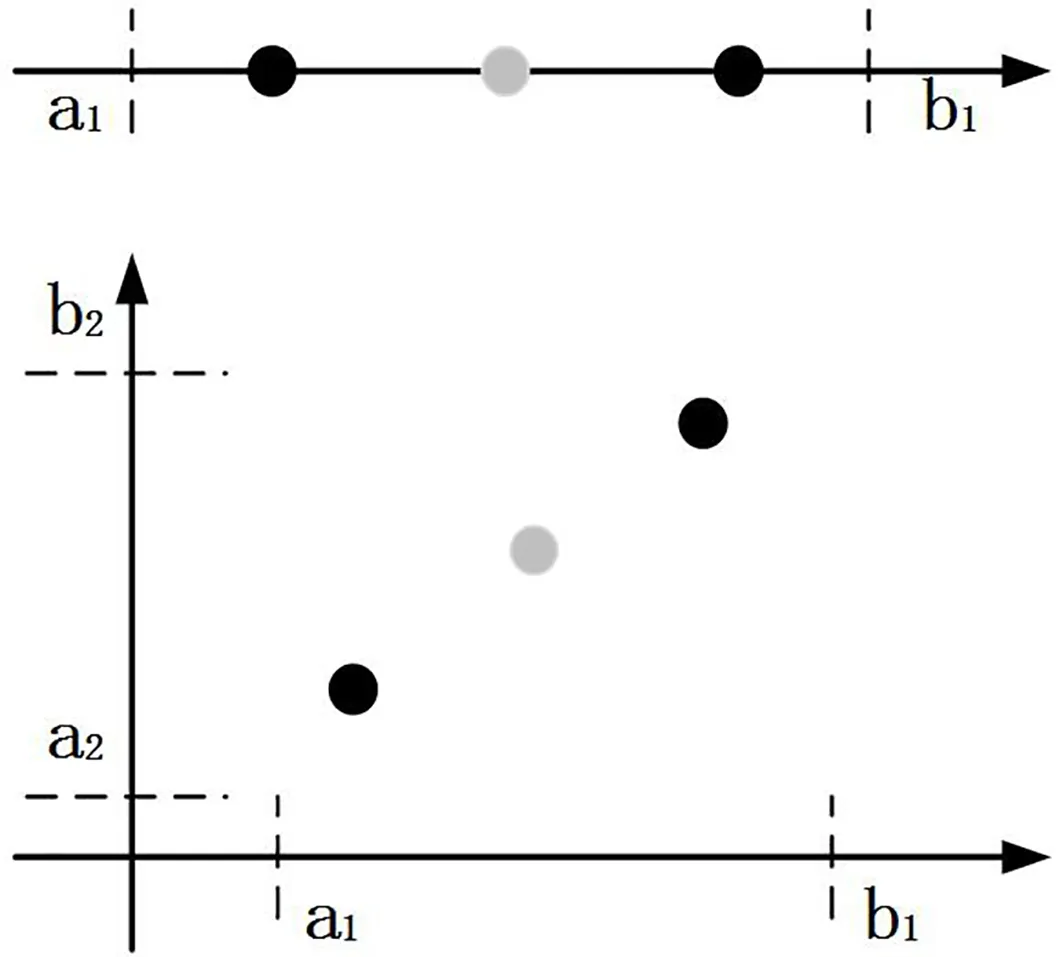
图1 反向点示意图

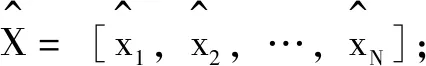
2.2 基于折迭交换的子种群分组方法

在传统SFLA中，分组方式是通过顺序的方式进行排列后分组的，该分组方式可能会使得越前面的组目标函数值越好，初始解越接近最优解，越后面的组目标函数值也差，初始解越远离最优解，有明显的解分配不均匀的情况。为了避免这种现象，改进的混合蛙跳算法中分组方式采用的是折迭交换的分组方式。

与传统分组方法相似，降序排列F个解。然后，将F个解分入M个组中，此时与传统方式不同于此处进行折迭分组，即第1个解编入Y1组，第2个解编入Y2组，直到第M个解编入YM组，然后将第M+1个解编入YM，第2×M个解编入YM-1组，……，第2×M个解编入Y1组，第2×M+1个解进入Y1组，第2×M+2个解编入Y2组……，以此类推，直到全部解被分到各个子种群内，此时，每组包含N个解，即F=M×N。将已经分好的M组解进行最优交换，若M为偶数，将第1组中目标函数最优解与第M/2组中目标函数最优解交换，第2组中目标函数最优解与第M/2+1组中目标函数最优解交换……以此类推，第M/2-1组中目标函数最优解与第M组中目标函数最优解交换；若m为奇数，则将第1组中目标函数最优解与第(M+1)/2+1组中目标函数最优解交换，第2组中目标函数最优解与第(M+1)/2+2组中目标函数最优解交换……以此类推，第(M+1)/2-1组中目标函数最优解与第m组中目标函数最优解交换，其中第(M+1)/2组中的解不变。通过此折迭交换方式，F个解被分为的M个组中每组仍含有N个解。

子种群进化完毕后，将进行各子种群融合步骤，在此过程中，会计算所有解的目标函数值，把这些目标函数值进行降序排列，目标函数值相同的个体仅保留一个。另外，若剩下的解没有F个，则随机生成所缺数量的解进行补足。

通过折迭交换过程进行的分组过程，可以使子种群分布更加均匀，确保种群的多样性，进而提高ISFLA收敛速度。

2.3 与粒子群算法融合的更新策略

2.3.1 粒子群算法简述

粒子群算法(Particle Swarm Optimization,PSO)的最初由来是根据鸟类群体在觅食过程中，会出现群体进化的现象，根据这种自然现象归纳出的一种智能群体优化算法[4]。具体思路可以概括为鸟群中包含N只小鸟，即种群中有N个粒子，其在存在于S维空间内，这N个粒子构成了目标函数的解，粒子之间是有相互协作和相互竞争的关系，通过这些过程找到待优化题目的最优解。将粒子的位置定义为xi=(xi1,xi2,…,xiS)，将粒子的移动速度定义为vi=(vi1,vi2,…,viS)，粒子i的最好位置记为pbi，全体粒子中最好位置的粒子位置记为gbi，i∈[1,N]。那么，在进化到第m次的时候，粒子的速度、位置分别通过以下的公式进行计算：

(2)

(3)

式中，i=1,2,…,N；j=1,2,…,S；ω为粒子移动速度的惯性权重系数；α、β为学习因子，代表粒子的个体学习能力，体现其向个体最优靠近或其他子种群及整个种群最优进化的特性，一般是正数；R1、R2为[0,1]之间均匀分布着的任意随机数。同时，粒子移动速度vij会设定一个特定范围，vij∈[-vmax,vmax]，用以规范具体问题的实际情况。

PSO作为应用较为广泛的高效搜索算法，兼备算法易实现、参数设置简单等优点，但与此同时，也伴随着算法易早熟、收敛速度慢的缺陷，因此在具体问题的实际应用中，通常会对算法依据适用性进行合理改进。

2.3.2 使用粒子群算法思想改进混合蛙跳算法

传统SFLA在子种群搜索更新过程中，在对子种群内最差解xw更新时，只结合了局部数据，这种模式会存在子种群内无法与全局信息进行交互，导致局部与全部信息不全面进行交流的问题。另外，在每次迭代过程中，青蛙最差个体的移动距离和最差解的更新与上一代没有信息交流，丢失了之前更新过程的信息，容易出现进化停滞、更新速度慢等问题。

基于上述问题，将ISFLA与PSO中局部极值与全部极值相结合的思想，在ISFLA子种群局部策略更新过程中同时结合局部最优解和全局最优解，从而达到算法过程里局部与全局信息充分交流的目的。同时，参考PSO算法主要思路，在子种群最差解更新过程中，引入上一轮子种群更新时的移动步长，并使用在对其取惯性权重后的值，通过惯性权重系数对青蛙移动步长和位置进行控制与调节，从而起到每一代青蛙个体的进化过程都与上一代的信息有交流，不会丢失原本的进化信息。那么，改进后的局部策略更新公式：

Di=ωDi-1+αR1(xb-xw)+βR2(xg-xw)

(4)

xw=(R+1)xw+Di

(5)

式中，α、β为学习因子，α决定子种群最优值对算法搜索水平的影响程度，α越大，则越多的个体会在子种群局部停留，β决定整个种群最优值对算法搜索水平的影响程度，β越大，则个体会越快停滞于全局最优值，依据大量实验结果，择优选取α=β=1.86；R、R1、R2分别为0～1的3个随机数；ω为上一代个体移动步长的惯性权重系数。

2.3.3 惯性权重系数的引入

惯性权重系数ω体现了个体移动趋势，若需防止种群内进化时出现局部最优解附近停滞进化的现象，则当更新后的最差解越接近局部最优解时，ω应该越大；若想要在全局最优解附近越细致搜索，则ω应该越小。综上，惯性权重系数公式：

(6)

式中，ωmax、ωmin为惯性权重系数的物质范围，分别代表ω的最大值、最小值，根据实际应用试验进行取值；g为子种群的当前进化代数；G为整个种群的预设进化代数。

同时，惯性权重系数的计算公式是非线性、递减函数，使得在算法初期最差解更新幅度大，局部搜索效率高；在更新后期最差解更新幅度小，适于精细搜索阶段，提高整个群体的更新效果，对优化结果起到重要改进作用。

2.4 基于小生境技术的种群淘汰机制

小生境原本描述的是一个生物学现象，指一个群体中会具有共同特性的个体存在[5]。这就好比在生物界中，往往相同或相似的物种会共同生活，在代代进化中，种群的个体逐渐通话，这就是生物的小生境现象。

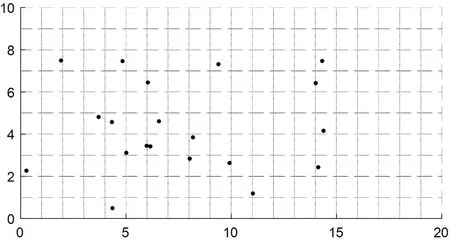
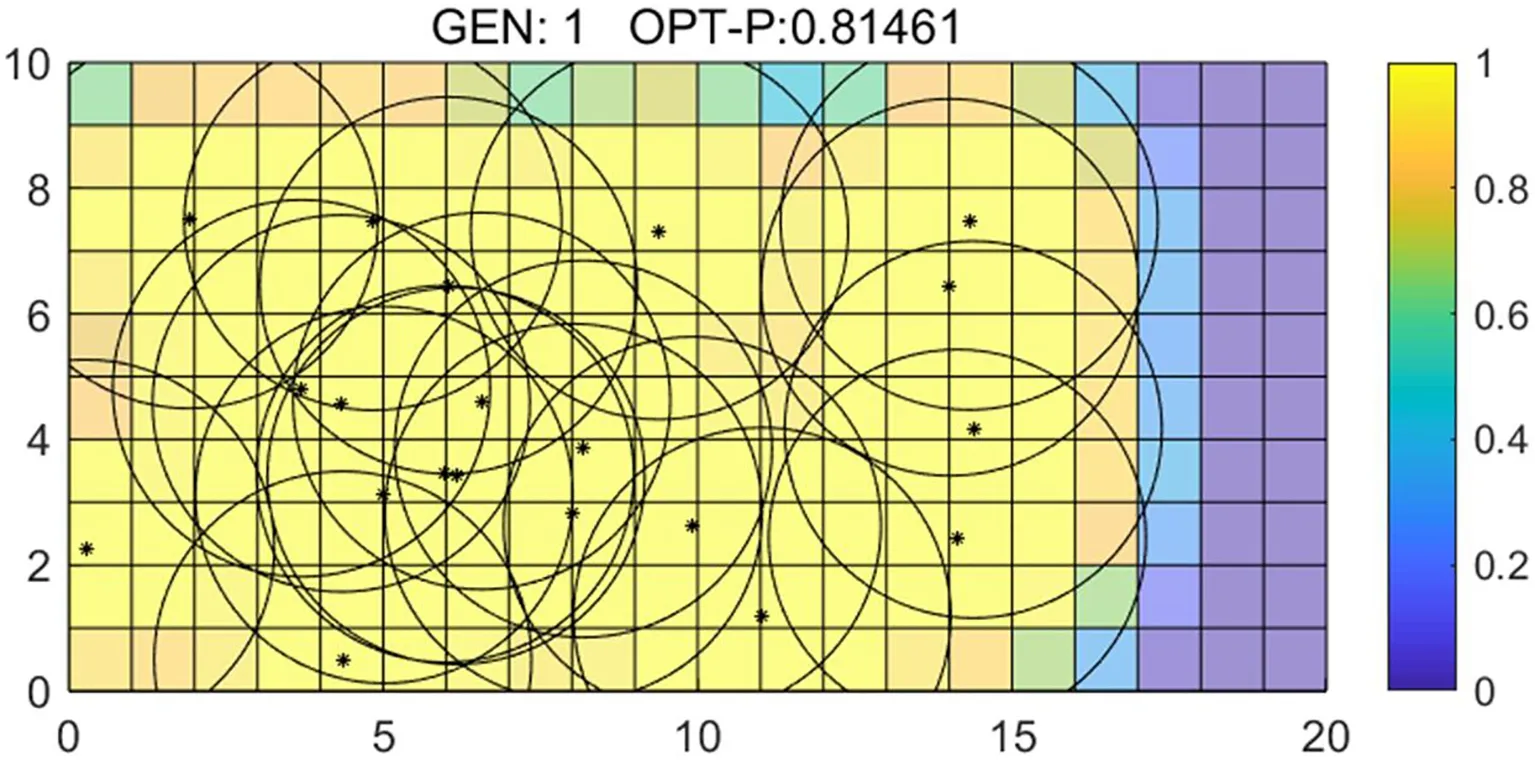
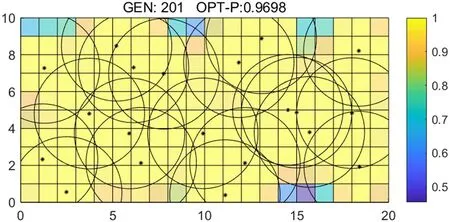
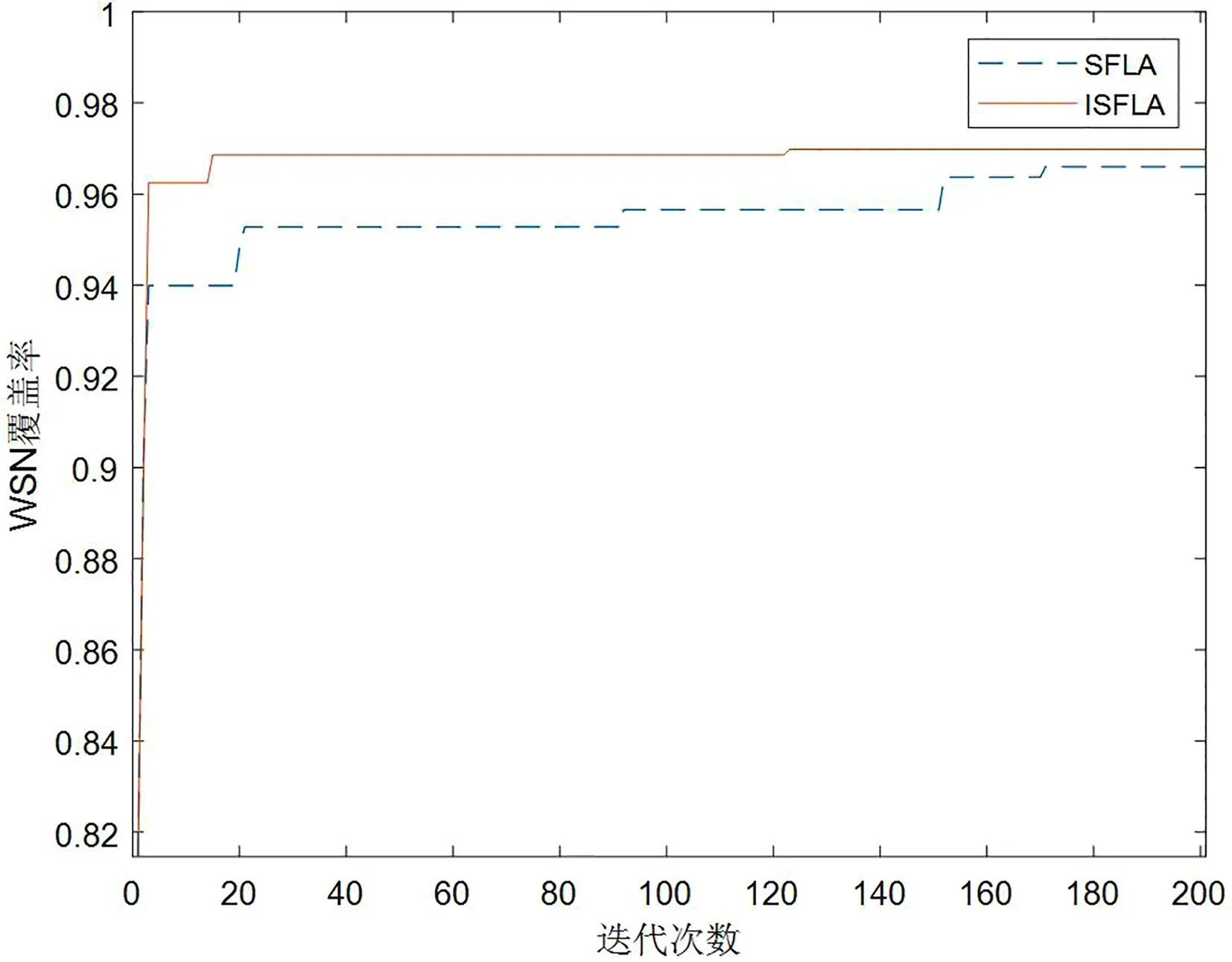
小生境的思想在优化问题中也具有实际应用价值，在优化问题迭代进化的过程中，任意两个个体间距离，记为d，这个距离为欧式距离[6]，再提前设定一个小生境距离，记为L，当d

欧式距离计算公式：

(7)

式中，i、j为子种群进化代数，2≤i≤N，2≤j≤N，且i≠j，N为子种群内进化代数；S是种群的维数；Xib、Xjb分别为子种群内第i代、第j代最优个体。

优化算法的智能化已经在许多生产生活领域中被广泛认可，但由于一些具体问题的复杂特性，使得算法在设计方面的难度也随之加大，伴随着算法的改进伴随而来的可能是一些收敛速度降低、易陷入局部解最优值的问题。以往的研究者对混合蛙跳算法的改进中也可能出现上述问题，为了避免这种弊端，将小生境思想结合到ISFLA中种群淘汰过程中，优化算法在迭代过程中出现的停滞缺陷。具体的应用思路是在子种群内部进行的局部搜索过程中，定义以下公式：

(8)

式中，Xib、Xjb为同一子种群内第i代、第j代最优个体，2≤i≤N，2≤j≤N且i≠j，N为子种群内进化代数；L为小生境距离；δ为小生境域值，一般取值为适当小的一个正数；f(Xib)、f(Xjb)分别某个子种群进化到第i代、第j代时，最优个体的目标函数值。这个公式的设计思路主要为当第i代、第j代进化过程中最优个体的欧氏距离小于L，并且2个最优个体的目标函差的绝对值小于δ时，即判定该子种群的进化状态接近停滞状态，随即将该子种群淘汰，并且重新初始化一个新的子种群代替淘汰子种群。

3 无线传感技术在农村电网运行监测中的应用仿真

农村电网运行监测覆盖问题是无线传感器网络研究中的重点问题之一，提高WSN覆盖率对提升农村电网自动化系统可靠性有着重要的意义。在传感器节点位置随机初始化后，监测区域内节点覆盖率则取决于节点感知半径、传输半径及节点位置等因素[7]。将改进混合蛙跳算法应用到优化网络覆盖率问题中，通过对其不断迭代优化，找到覆盖率最大的一组节点分布，以提高WSN覆盖率，减少节点冗余，提升网络整体性能。

3.1 无线传感器网络节点模型

把监测区域拟作二维空间，定义为S，在S中包含N个传感器节点，把这些节点的集合定义为s={s1,s2,s3,…,sN}，其中，第i个节点定义为si，同时，针对该WSN系统有如下约定：在WSN监测区域内所有传感器节点感知半径相同，均定义为r；通信半径也都相同，均定义为R，并且使得能够确保整个网络连通性以及防止无线干扰，设定R=2r。

各个节点的坐标位置都已知。设WSN内第i个节点的位置定义为(xi，yi)，优化思想为通过移动节点位置以提高WSN覆盖率。把监测区域S离散化，将其横向数字离散成m个点，纵向n个点，则S=m×n。随后，将离散后的像素点定义为p，p点位置定义为(x，y)，则其点p的位置与每个传感器节点之间的长度即：

(9)

根据监测区域可能受环境等外界因素影响，不能用仅能区分感知或不能感知的0、1模型仿真，所以此处选择的是更为贴近现场情况的概率感知模型[8]，概率模型公式定义：

(10)

式中，d(si，p)为传感器节点si与点p之间的长度；re为传感器节点测量可靠参数；λ1，λ2，β1，β2为与节点特性有关的测量参数；α1，α2为输入参数。输入参数α1，α2的计算公式定义：

(11)

因此，监测区域中全部像素点p的监测结果，及WSN中所有传感器节点的联合覆盖率：

(12)

将WSN覆盖率可以定义为所有传感器节点覆盖面积与监测地区面积的比值[9]，记为Parea，公式：

(13)

式中，m×n为监测区域S的面积。

对WSN覆盖优化问题即转换成为在节点位置已知的情况下，通过ISFLA算法对覆盖率进行进行优化，并在在覆盖率最大的情况下找出最优传感器节点位置。

3.2 基于改进蛙跳算法的无线传感器网络覆盖优化

无线传感器网络覆盖的优化主要依托于与算法的结合。一直以来很多研究者将遗传算法、灰狼算法、蚁群算法等群智能算法应用到提升覆盖率的研究中，但效果始终差强人意，往往存在寻优结果慢或早熟等优化问题。针对这些问题，将改进混合蛙跳算法应用到WSN覆盖问题的研究中，从通过改进后算法优化能力有所提升的角度来提高网络覆盖率，从而提升网络性能，达到优化系统的效果。

3.2.1 基于ISFLA的无线传感器网络覆盖算法

在改进混合蛙跳算法的覆盖优化研究中，将监测区域内每个传感器节点的位置假设为一个青蛙，定义为F，将F个青蛙再分成m组，即子种群，每一个子种群中都存在n个青蛙，且每个青蛙在移动的时候步长最大值为Dmax，在ISFLA中需要进行N次组内迭代，整个种群的进化上限是G代。即设有F个传感器节点，即种群规模为F，每个子种群内个体数量为n个，子种群个数m组。每个传感器节点的最大移动距离为Dmax，设定每组内更新代数为N，全局的最大进化代数为G。

每一个青蛙都代表着一个位置，其位置结构决定了WSN覆盖率的大小。将ISFLA应用到优化WSN覆盖的基本思想就是将传感器节点的位置作为算法输入，再将网络覆盖率作为适应度函数，利用ISFLA算法对网络覆盖率进行优化，从而找到覆盖率最大时传感器节点的分布情况。

3.2.2 网络覆盖优化算法实现

基于ISFLA算法的WSN覆盖优化具体步骤如下。

Step1对ISFLA算法、概率覆盖模型需要设置的参数进行参数初始化。

Step2将网络覆盖率作为适应度函数，利用ISFLA算法在迭代次数内或终止条件生效前不断更新传感器节点位置。

Step3判断是否达到预定的混合迭代次数，若没有达到，则转入Step3，否则算法结束。

其工作流程图如图2所示。

图2 基于ISFLA算法的WSN覆盖优化工作流程图

3.3 仿真实验设置

将WSN设置于一个20×10m2的区域内，在该监测区域内随机安放20个无线传感器节点，所有节点的感知半径、通信半径都是相等的，设感知半径r=3m，通信半径R=6m，在仿真应用中的概率模型参数部分，参数取值分别为λ1=1，λ2=0，β1=1，β2=1，re=0.5r=1.5m，并通过Matlab软件进行仿真。

3.4 仿真实验分析

为了对比分析算法的性能，将传感器节点初始位置设置为已知相同量，节点初始位置随机生成，如图3所示。其中，20×10m2的长方形为WSN监测区域，“·”为随机分布的传感器节点位置。在图4～6中以节点为圆心的圆圈内为节点感知范围，颜色由深至浅即表示覆盖率由低至高。

图3 初始节点位置

在仿真实验中，20个传感器分别通过SFLA算法和ISFLA算法部署在监测区域内。通过图5、图6可以看出，覆盖面积有明显的优化效果，未覆盖面积逐渐变小，ISFLA优化后的节点位置变得更加均匀，覆盖范围更广，网络传输性能有明显的提升。

图4 初始网络覆盖区域

图5 SFLA算法优化后节点分布及覆盖区域

图6 ISFLA算法优化后节点分布及覆盖区域

图7 SFLA、ISFLA算法覆盖优化曲线

根据图7所示，可以明显看出通过ISFLA算法优化后的网络覆盖率更大，并且收敛速度也比SFLA要快很多，有效改善ISFLA陷入收敛停滞的问题，优化后的节点分布也较为均匀，使得WSN可以更好地感知监测区域内需要监测的目标及实际情况。

4 结束语

在农村电网运维过程中应用基于改进混合蛙跳算法的无线传感器网络技术能够准确、大范围的获取设备运行信息，为农村电网建设发展提供技术支持，在极大程度上推动农村农业发展。随着经济水平的提升和科学技术的成熟，加之网络、物联网和现代信息技术的协调发展，必会推进农业无线传感技术向实用化、定量化、科学化、产业化方向发展，为促进我国农业的现代化发展奠定基础。