基于连续镜面变形镜本征模方法的复杂涡旋光场调控

熊光昀，唐奥，兰斌，沈锋*

1中国科学院自适应光学重点实验室，四川 成都 610209；

2中国科学院光电技术研究所，四川 成都 610209；

3中国科学院大学，北京 100049

1 引 言

涡旋光束是一种中空的环状光束，其携带螺旋相位导致其每个光子都带有lћ的轨道角动量(orbital angular momentum,OAM)，其中l为拓扑荷数，也称模式数，不同的拓扑荷数代表不同模式的涡旋光束[1]，拓扑荷数理论上是可以取无限量的值。因为其特殊的性质，涡旋光束引起了广泛的关注，并在很多领域有重要的应用。例如，因轨道角动量可以传递给微小粒子而应用于光学捕获及光学操纵领域[2-5]。因不同的模式相互正交且模式无限量而应用于光学通信[6-14]，在光学加工[15-16]和光学测量[17-21]等领域有着诸多应用。另外，在大气湍流[22]和海洋湍流[23]中的传输问题也被研究。在以往的研究中，生成涡旋光束的方法通常分为两类，第一类为腔外法，如空间光调制器法[24-28]、螺旋相位板法[29]、超表面法[30]、模式转换法[31-32]以及角锥阵列法[33-34]等；第二类为腔内法，如点损耗法[35]、离轴泵浦法[36]、空间光调制器法[37]以及环形光泵浦法[38-39]等。但是这些方法通常不能兼顾耐受高功率的激光输出和对拓扑荷数的灵活调控。而在基于OAM模式的数据传输领域，高功率输出和拓扑荷数灵活变换的结合更具有实际意义，更为重要[40-42]。因此，如何生成可以耐受高功率激光输出并且可以灵活调控拓扑荷数的涡旋光束是一个待解决的重要课题。

变形反射镜(Deformation mirror,DM)是自适应光学系统的关键器件，用于补偿大气湍流产生的像差[43]，并适用于高功率激光的工作环境[44]。早在1983 年，研究人员指出连续镜面变形镜无法拟合位错相位[45]，因此已有的关于变形镜产生涡旋光束的报道均为分段变形镜[46-50]，而分段变形镜不能承受高功率，这是由于其子镜间存在间隙，高功率激光会透过间隙对变形镜内部造成损伤。在我们之前的工作中，已经实现了连续镜面变形镜对涡旋光束的生成，完美的兼顾耐受高功率输出和模式可调的优点[51]。但是该工作中变形镜驱动器电压的计算方法并不具有普适性，对于其他复杂的涡旋波前，如分数阶或OAM 叠加态的波前，难以求解，不能做到对各种波前的灵活调控。因此本文考虑采用一种新的计算方法，对之前工作做出更大的改进。在连续镜面变形反射镜拟合波前的研究中，通常有两类方法。第一类为无模型法，这类方法通常优化一个像质评价函数至函数收敛，达到对目标波前的最优拟合，如遗传算法[52]、模拟退火算法[53]、随机并行梯度下降算法[54]等。这些方法一般需要多次迭代，收敛速度缓慢，难以做到拓扑荷数的灵活调控。第二类为模式法，如Zernike 模式法[55-56]、Lukosz 模式法[57]以及本征模法[58-62]。这类方法先确定一组完备正交的模式，计算模式系数，通过对各个模式的线性叠加来完成对目标波前的拟合。其中Zernike 模式在圆域正交，Lukosz 模式在圆域上导数正交，且Lukosz 模式法无需多次迭代从而使算法的实时性得到提高。然而通常变形镜的分布并不是圆域，例如本文使用的变形镜驱动器排布为环域，此时再用到这两种模式法则需要重新构建正交基。而变形反射镜的本征模是由变形镜驱动器的影响函数直接精确导出，因此不仅避免了拟合误差的影响，提高了拟合精度，还能够适应不同排布的变形镜。

本文中采用连续镜面变形反射镜的本征模法，针对拓扑荷数为-5～5 的整数阶、拓扑荷数绝对值在5以内的分数阶、多分数阶、叠加态的螺旋波前的拟合进行了仿真分析，动态调控生成了各种涡旋光场。结果显示，采用连续镜面变形反射镜对高功率涡旋光场的调控领域具有很好的应用前景。

2 研究方案

2.1 变形镜

变形镜由镜面、驱动器和底座组成，每一个驱动器对应一个影响函数，通过对各个驱动器施加不同驱动电压，使对应位置的镜面产生不同的形变，来拟合波前信息。本文所采用的变形镜的排布与文献[51]中的相同，如图1 所示，为连续镜面变形反射镜生成涡旋光束的示意图。

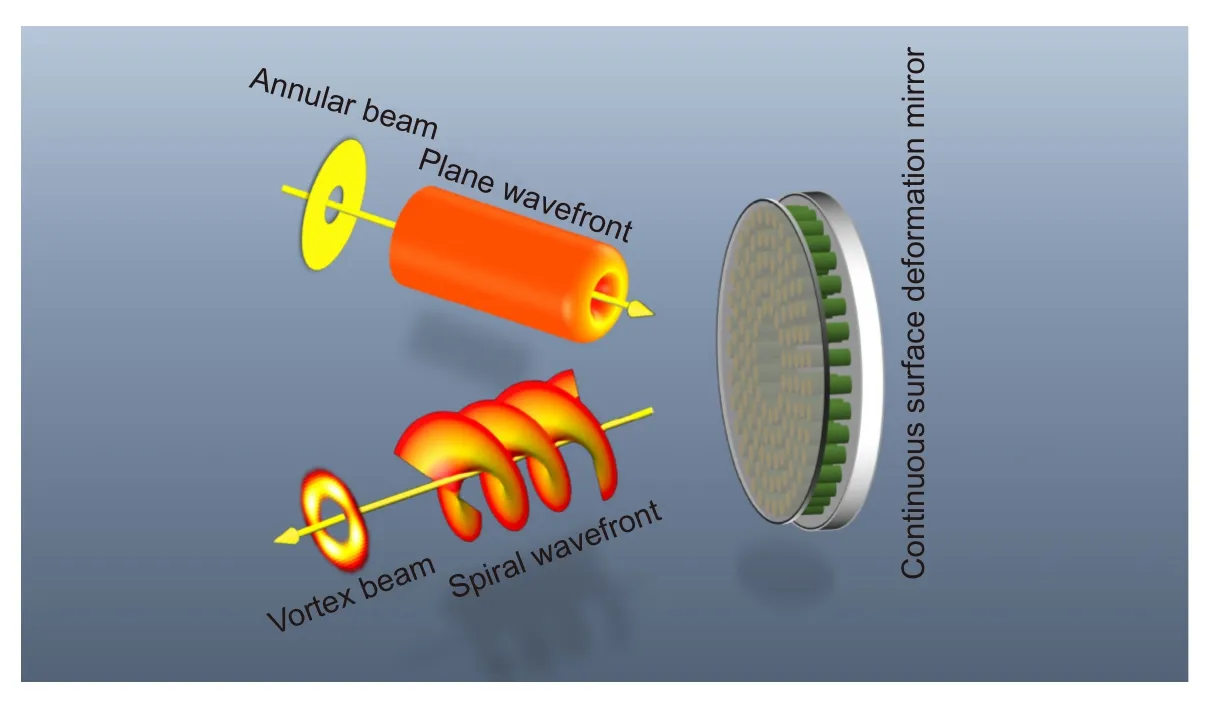
图1 连续镜面变形反射镜生成涡旋光束的示意图Fig.1 Schematic diagram of the vortex beam generated by continuous mirror deformation mirror

2.2 使用本征模法生成涡旋光场

本文拟合涡旋光束的螺旋波前信息用的是基于变形镜的本征模法。第一步是将非正交的影响函数构造成正交的本征模，过程如下：

定义影响函数F(x,y)之间的耦合系数矩阵C：

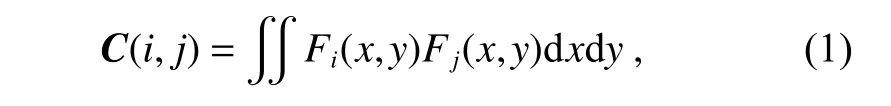
其中：i为驱动器的次序。再对耦合矩阵C进行奇异值分解：

式中：S为矩阵C的特征值所构成的对角矩阵，另外矩阵U、V满足关系U×V=E，E为单位矩阵。通过矩阵U，则可以构造出变形镜的本征模Mi(x,y)：

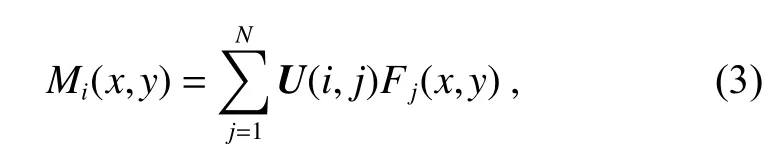
式中：N为驱动器的个数。

第二步是将需要拟合的目标波前φ0(x,y)与本征模Mi(x,y)做内积运算，求得本征模系数mi：

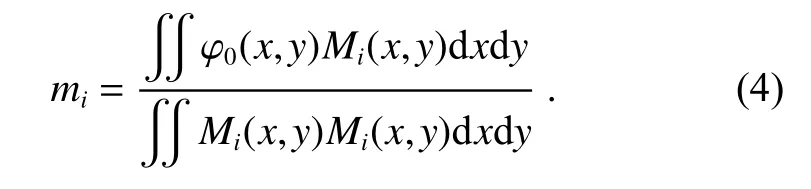
第三步是拟合波前，在仿真过程中，将本征模按本征模系数线性叠加得到拟合波前φ(x,y)。如下式：

而在实际实验中还需通过本征模系数矩阵m求出驱动器电压矩阵v，加载到变形镜上，得到φ(x,y)：

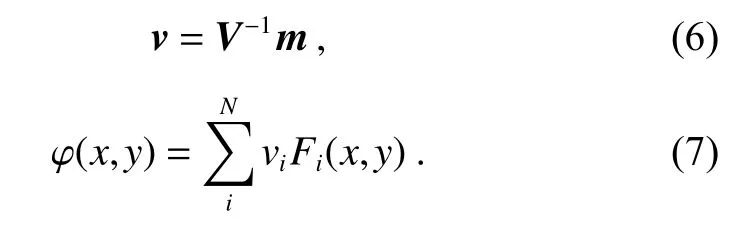
式(6)中的V与式(2)中的V相同。

在整个过程中，变形镜的布局和驱动器影响函数是确定的，而本征模仅由驱动器影响函数及其布局分布决定，所以本征模也是确定的。因此，在拟合波前之前，本征模已预先求算出来。在拟合波前时，对于不同的拟合需求，仅需改变输入的目标波前即可，这一优点使得驱动电压的计算更加方便。这一过程所需时间很短，这也是本征模法能够动态调控涡旋光束的一个前提。

2.3 仿真过程

如图2 所示，为使用变形镜生成涡旋光束的示意图，设需要拟合的光场为E(x,y)，相位为目标波前φ0(x,y)。按2.2 节中方法得到拟合波前φ(x,y)并加载在变形反射镜上之后，根据图2 中的光路图，一束环形平面光照射在变形反射镜上，会附带上拟合波前成为涡旋光束。透镜L1用来观察其远场衍射结果，u2为透镜L1、L2的焦面，当涡旋光束传播至此处时，光场通常存在旁瓣，相位存在高频噪声，衍射结果并不理想，这是由于变形镜驱动器分布的内外环半径并不适合每一个拓扑荷数的涡旋光束，另外变形镜不能拟合螺旋相位中的相位奇点，对于0～2π 的突变相位，只能拟合一个倾斜相位来代替，因此产生难以避免的误差。透镜L1、L2、L3组成的4f 滤波系统用来消除u2处的误差，使其更接近理想值。

如图2 所示，经变形镜反射之后u1处的光场E1可以表示为

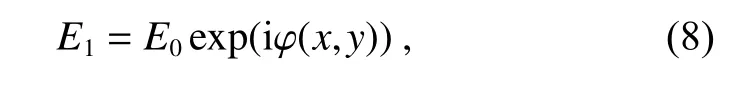
其中：E0表示振幅信息，取环状光瞳，u2处光场E2可以由E1的傅里叶变换来表示：

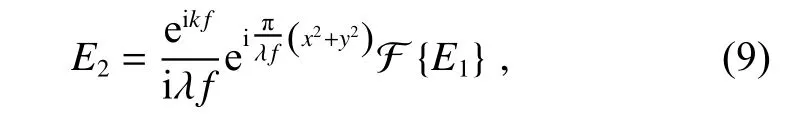
其中：f为图2 中的焦距，经过u2处小孔之后的光场E3可以表示为

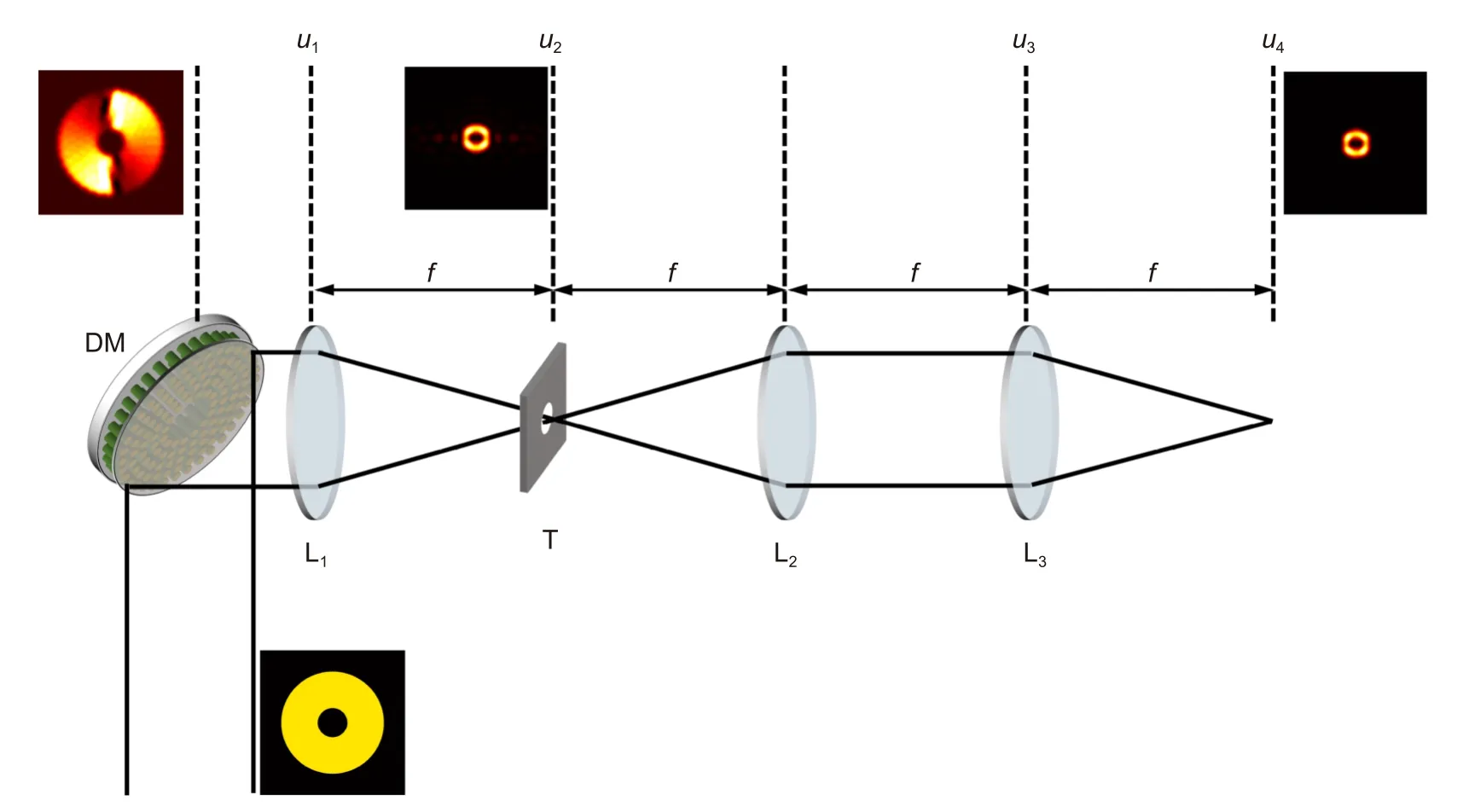
图2 使用变形镜生成涡旋光束的示意图。L1、L2、L3：凸透镜；T：孔径光阑；DM：变形镜；f：焦距Fig.2 Schematic diagram of using DM to generate vortex beams.L1,L2,L3: convex lens;T: aperture;DM: deformation mirror;f: focal length

其中：t为透过率函数。t表示为

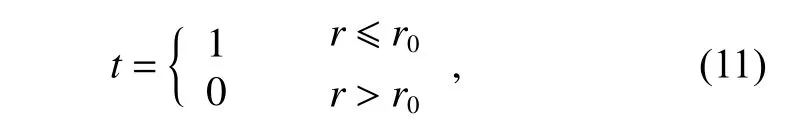
其中：r0为孔径光阑的半径，滤波之后u3处的光场是E3的逆傅里叶变换，u4处得到经过滤波后的涡旋光场的远场信息。

3 仿真结果

3.1 整数阶涡旋光束

图3 (a)～3(e)为拓扑荷数为1～5 的目标波前，图3(f)～3(j)是由本征模法拟合得到的螺旋波前。可以看出拟合效果较好，波前较光滑，整体来看，本征模法具备较好的拟合螺旋波前的能力。如图4 (a)和4(c)为拓扑荷数为2 的拟合波前在u2处的光强和相位，光强呈现中空环状结构，相位呈螺旋状，且有2个相位奇点。经过滤波处理之后在u4处的光强及相位如图4 (b)和4(d)，可以明显看到图4 (a)中旁瓣和图4 (c)中高频噪声被完全消除。

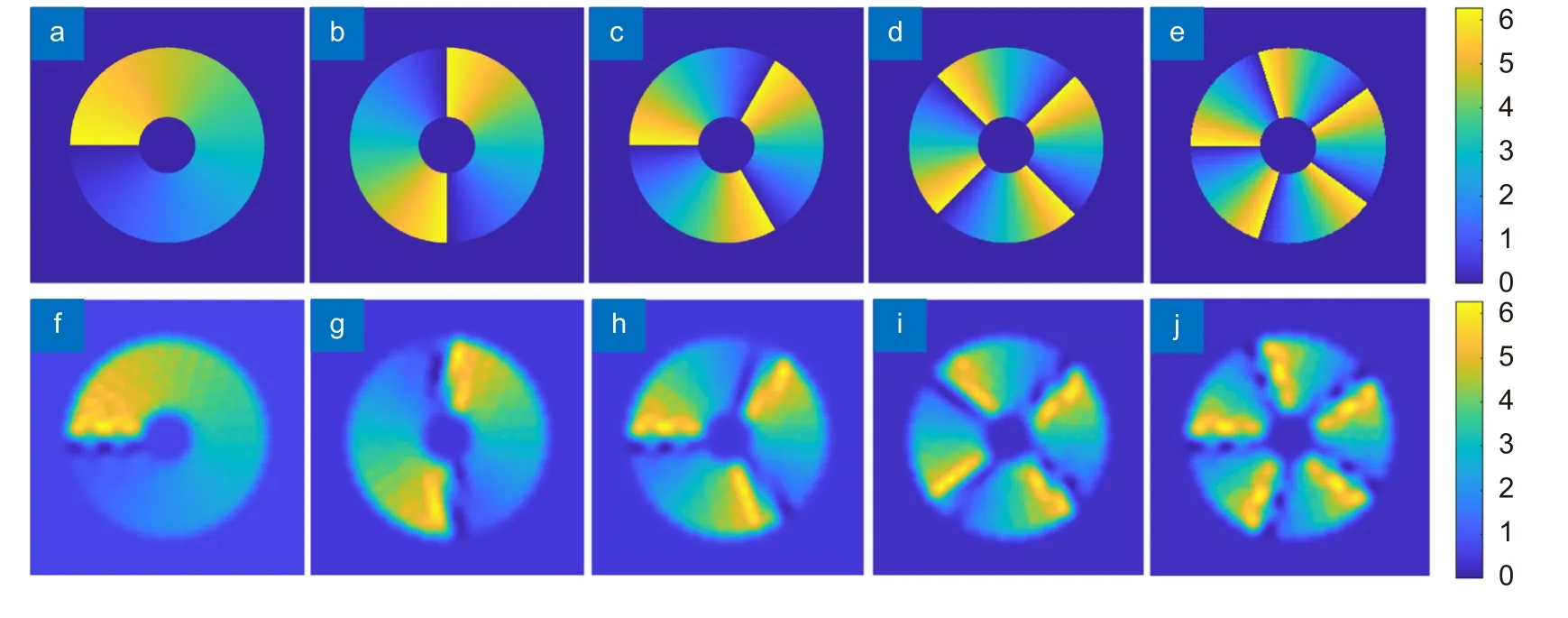
图3 整数阶螺旋波前的拟合。(a)～(e) 拓扑荷数为l=1～5 的整数阶目标波前;(f)～(j) 拓扑荷数为l=1～5 的整数阶拟合波前Fig.3 Fitting of the integer order spiral wavefront.(a)～(e) Target wavefront with the integer order l=1～5;(f)～(j) Fitting wavefront of the integer order l=1～5

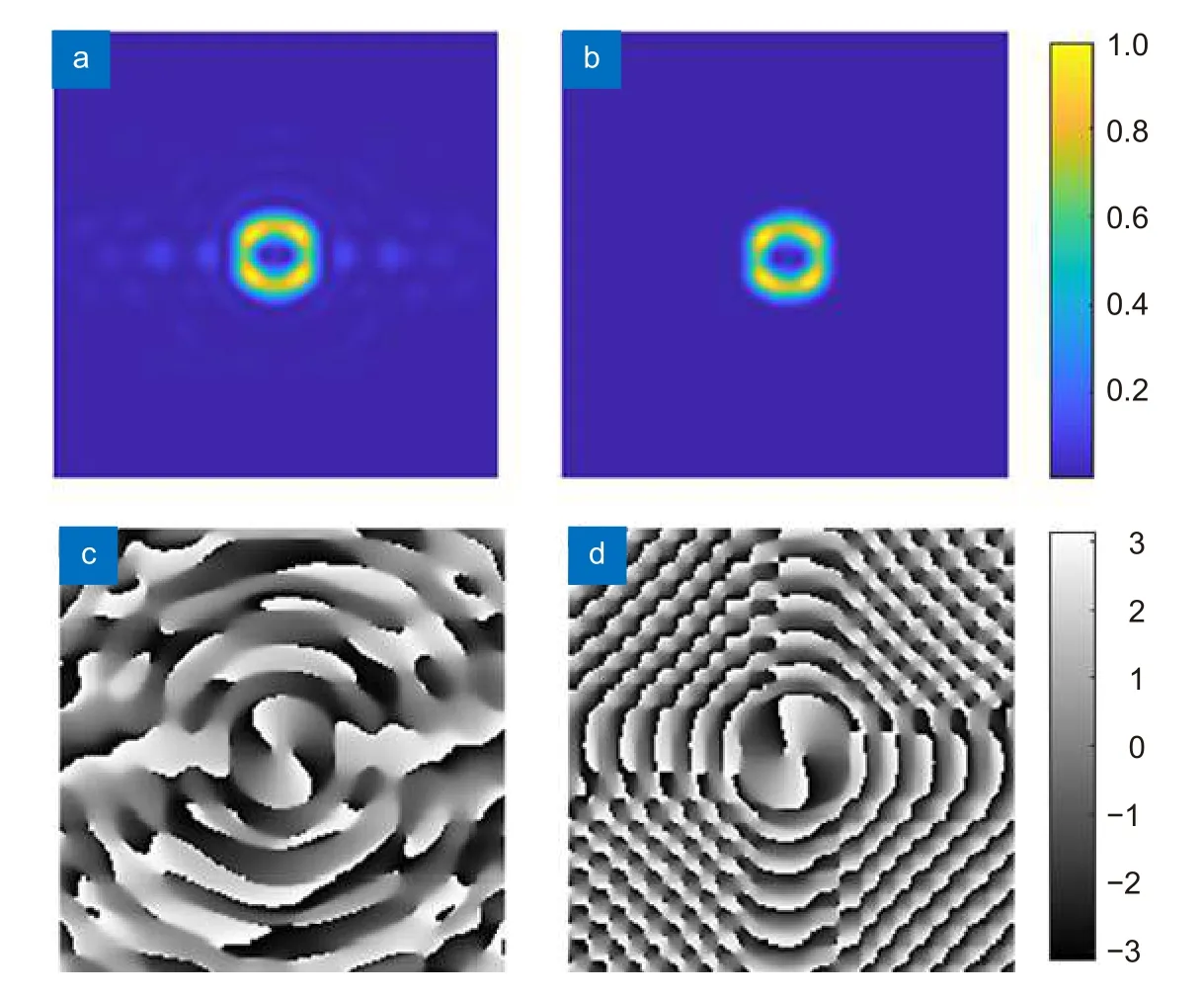
图4 拓扑荷数为2 的涡旋光束的拟合。(a) u2 处未滤波的光强;(b) u4 处经过滤波的光强;(c) u2 处未滤波的相位;(d) u4 处经过滤波的相位Fig.4 Fitting of integer order vortex beams with topological charge is 2.(a) Unfiltered intensity at u2;(b) Filtered intensity at u4;(c) Unfiltered phase at u2;(d) Filtered phase at u4

图5 为拓扑荷数等于1、3、4、5 的拟合波前经过滤波处理之后的结果，l=2～5 的光场由一系列光斑组成，呈现光强分立的现象。这是由于连续镜面变形反射镜不能拟合突变相位，造成的误差在聚焦过程中破坏了光场的环形结构[51]。而各个模式的光强均有中空环状的特点，且相位均为螺旋状，每个相位都带有与拓扑荷数相对应数量的相位奇点，拟合效果较为理想。

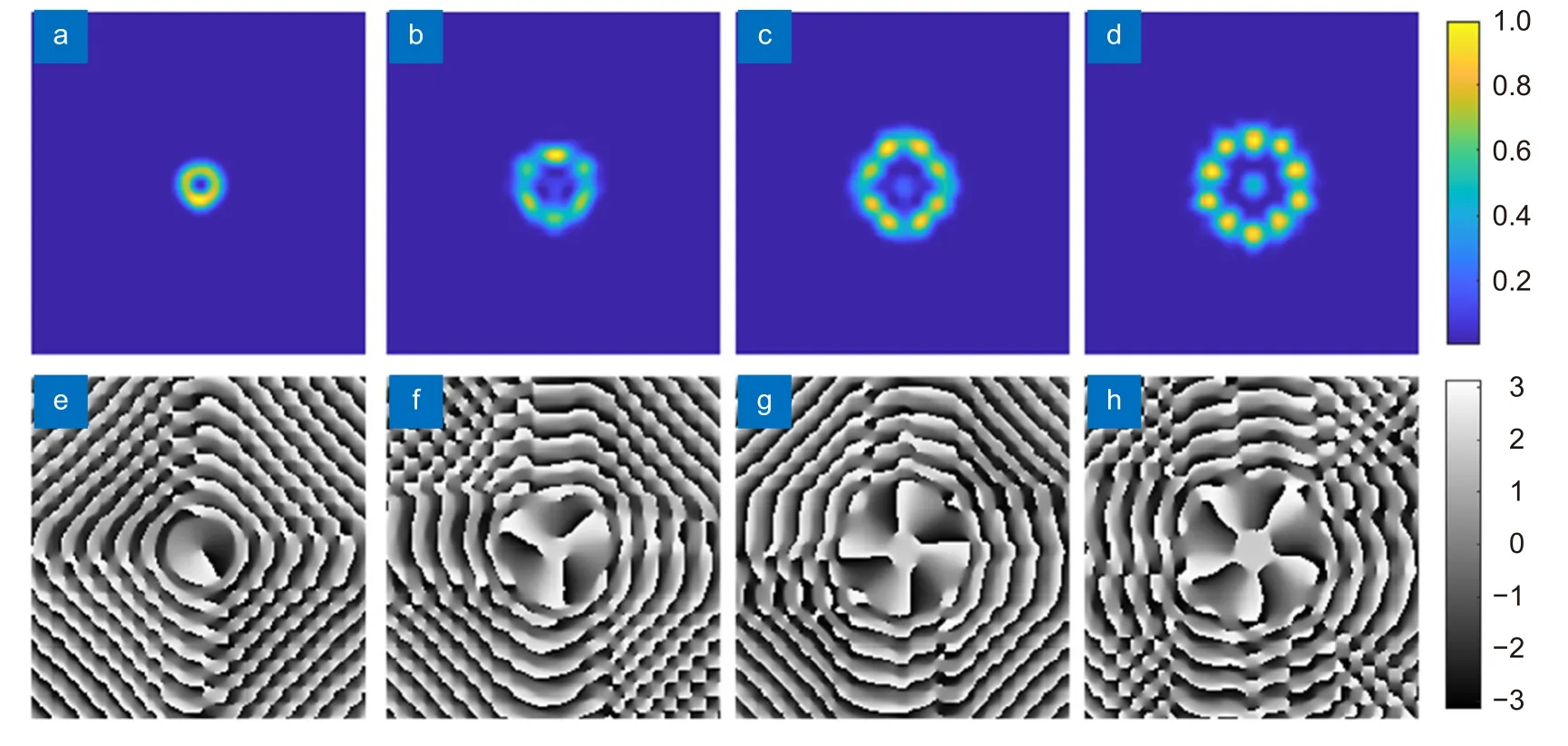
图5 整数阶拟合波前在经过滤波处理后的光场及相位。(a)～(d) 拓扑荷数为1、3、4、5 的光强；(e)～(h) 拓扑荷数为1、3、4、5 的相位Fig.5 The light field and phase of the integer order vortex beam after focusing and filtering.(a)～(d) Intensity with topological charges l=1,3,4,and 5;(e)～(h) Phase with topological charges l=1,3,4,and 5

各个模式拟合结果的模式纯度[63]分别为0.9792(l=1)、0.9769(l=2)、0.9645(l=3)、0.9671(l=4)、0.9163(l=5)。平均值为0.958，这表明变形镜用本征模法完全具备产生涡旋光束的能力，结合滤波系统可以使涡旋光束更理想。

3.2 分数阶涡旋光束

分数阶涡旋光束的拓扑荷数为分数，具有自旋光场，可以对内或对外捕获和旋转粒子。与整数阶涡旋光束不同，分数阶涡旋光束有一个径向开口，提供了一种捕获与释放微粒的可取方案[64]。

图6 为拓扑荷数为分数阶涡旋光束的目标波前和由本征模法得到的拟合波前。从图中可以看出，两组结果基本一致，本征模法同样具备对分数阶螺旋波前的拟合能力。

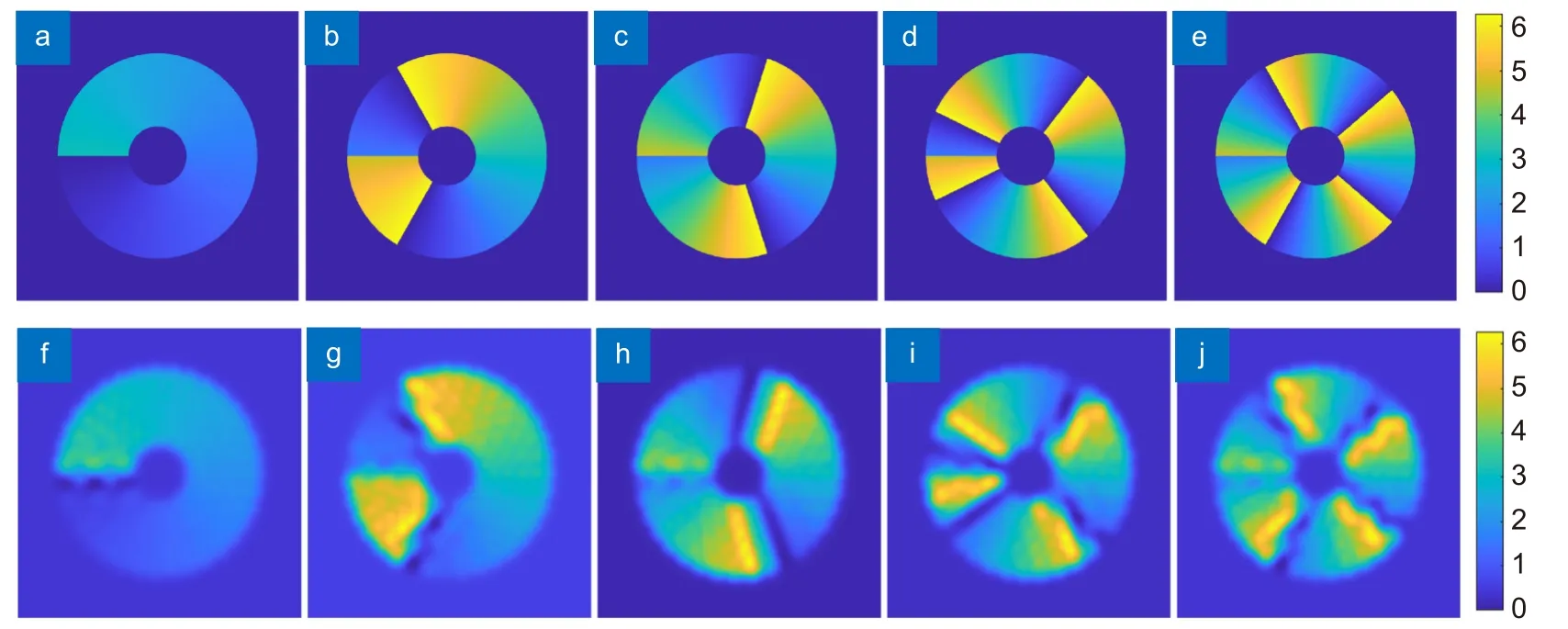
图6 分数阶螺旋波前的拟合。(a)～(e) 拓扑荷数为l=0.5、1.5、2.5、3.5、4.5 的目标波前；(f)～(j) 拓扑荷数为l=0.5、1.5、2.5、3.5、4.5 的拟合波前Fig.6 Fitting of the fractional order spiral wavefront.(a)～(e) Target wavefront with topological charges l=0.5,1.5,2.5,3.5,and 4.5;(f)～(j) Fitting wavefront with topological charges l=0.5,1.5,2.5,3.5,and 4.5

图7 为由本征模法得到的分数阶目标波前与拟合波前经过滤波处理后的光场结果，图8 为分数阶目标波前与拟合波前经过滤波处理后的相位结果。但是这一节分数阶涡旋光场以及3.3 节多分数阶涡旋光束的拟合结果无法用模式纯度作为评价指标，这是因为模式纯度的计算是基于整数阶OAM 模式之间的正交性，分数阶OAM 模式无法计算。但从仿真图来看，两组结果基本一致，由本征模法得到的光场依旧保持中空环状结构，存在光强分立的现象，且相位呈螺旋状。因此，变形反射镜的本征模法具备对于分数阶涡旋光束的拟合能力。

图7 分数阶涡旋光束的滤波结果。(a)～(e) 拓扑荷数为l=0.5、1.5、2.5、3.5、4.5 的目标波前在u4 处的光强;(f)～(j) 拓扑荷数为l=0.5、1.5、2.5、3.5、4.5 的拟合波前在u4 处的光强Fig.7 Filtering results of the fractional order vortex beam.(a)～(e) Intensity of target wavefront with topological charges l=0.5,1.5,2.5,3.5,and 4.5 at u4;(f)～(j) Intensity of fitting wavefront with topological charges l=0.5,1.5,2.5,3.5,and 4.5 at u4

图8 分数阶涡旋光束的滤波结果。(a)～(e) 拓扑荷数为l=0.5、1.5、2.5、3.5、4.5 的目标波前在u4 处的相位;(f)～(j) 拓扑荷数为l=0.5、1.5、2.5、3.5、4.5 的拟合波前在u4 处的相位Fig.8 Filtering results of the fractional order vortex beam.(a)～(e) Phase of target wavefront with topological charges l=0.5,1.5,2.5,3.5,and 4.5 at u4;(f)～(j) Phase of fitting wavefront with topological charges l=0.5,1.5,2.5,3.5,and 4.5 at u4

3.3 多分数阶涡旋光束

分数阶涡旋光束可以解释为一系列包含不同OAM 状态的整数阶涡旋光束的加权叠加。而李新忠提出的多分数阶涡旋光束的概念可以精确控制各个权重系数以及OAM 的状态，在基于OAM 的光学通信技术领域具有潜在应用价值[65]。变形反射镜的本征模法可以很好地对其进行拟合。

图9 (a)和9(b)分别为以l=3、4 为初始波前，在每一个0～2π 渐变相位中插入0～π 的渐变相位得到的目标波前。图9 (c)和9(d)为本征模法得到的拟合波前，可以看出拟合效果依旧不错。

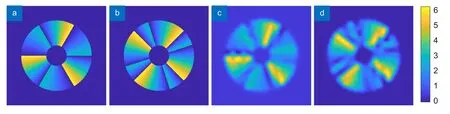
图9 多分数阶螺旋波前的拟合。(a),(b) 目标波前；(c),(d) 拟合波前Fig.9 Fitting of multi-fractional spiral wavefront.(a),(b) Target wavefront;(c),(d) Fitting wavefront

如图10 所示，10(a)、10(b)和10(e)、10(f)分别为目标波前经过滤波处理得到的光场及相位结果，10(c)、10(d)和10(g)、10(h)分别为由本征模法得到的拟合波前所得结果。两组结果基本一致，因此，本征模法具备对多分数阶涡旋光束的拟合能力。

图10 多分数阶目标波前及拟合波前在滤波处理后的光场及相位。(a),(b) 多分数阶目标波前在u4 处的光强;(c),(d) 多分数阶拟合波前在u4 处的光强;(e),(f) 多分数阶目标波前在u4 处的相位;(g),(h) 多分数阶拟合波前在u4 处的相位Fig.10 The light field and phase of the multi-fractional order target wavefront and the fitting wavefront after filtering.(a),(b) Intensity of multi-fractional order target wavefront at u4;(c),(d) Intensity of multi-fractional order fitting wavefront at u4;(e),(f) Phase of multi-fractional order target wavefront at u4;(g),(h) Phase of multi-fractional order fitting wavefront at u4

3.4 叠加态涡旋光束

当拓扑荷数为相反数的两束涡旋光束叠加时，光场和相位均为花瓣状，称为叠加态涡旋光束。叠加态涡旋光束比单个涡旋光束具有更多的轨道角动量，在微粒操纵领域具有更大的潜力，可以应用于对微粒的三维操纵[66]。本文仍用本征模法对其进行拟合。

如图11 所示，11(a)～11(d)分别为l=±1、±2、±3、±4 的涡旋光束相叠加得到的目标波前，其均为0 与π 的叠加。用本征模法拟合得到的结果为图11(e)～11(h)，可以看出本征模法依旧适用。

图12 为叠加态涡旋光束的拟合波前经过滤波处理后得到的光场及相位结果，可以看出光场均为均匀对称的花瓣状，且花瓣的个数与其拓扑荷数相关，这与引文[66]中结果一致。相位结果也与图11 中目标波前基本一致。不同于3.2 节分数阶涡旋光束和3.3节多分数阶涡旋光束的是，叠加态涡旋光束本质上是两个整数阶涡旋光束的叠加，因此可以用模式纯度作为评价指标。叠加态涡旋光束的模式纯度计算结果如图13 所示，l=±1 的叠加态涡旋光束的模式纯度分别为0.465 (l=-1)，0.4398 (l=+1)；l=±2 的叠加态涡旋光束的模式纯度分别为0.4255 (l=-2)，0.4307 (l=+2)；l=±3 的叠加态涡旋光束的模式纯度分别为0.4355(l=-3)，0.4309 (l=+3)；l=±4 的叠加态涡旋光束的模式纯度分别为0.4316 (l=-4)，0.4316 (l=+4)。由此可以得出结论，在叠加态涡旋光束的滤波结果中，所包含的两个模式的占比基本持平，均为0.4～0.5，说明本征模法具备对于叠加态涡旋光束的拟合能力。

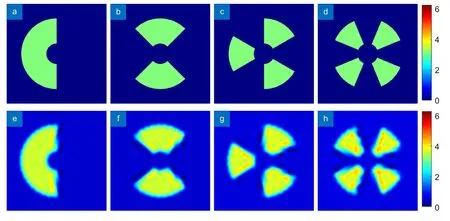
图11 叠加态目标波前及拟合波前。(a)～(d) 拓扑荷数分别为l=±1、±2、±3、±4 的目标波前;(e)～(h) 拓扑荷数分别为l=±1、±2、±3、±4 的拟合波前Fig.11 Superposition target wavefront and fitting wavefront.(a)～(d) Target wavefront with topological charges l=±1,±2,±3,and ±4;(e)～(h) Fitting wavefront with topological charges l=±1,±2,±3,and ±4

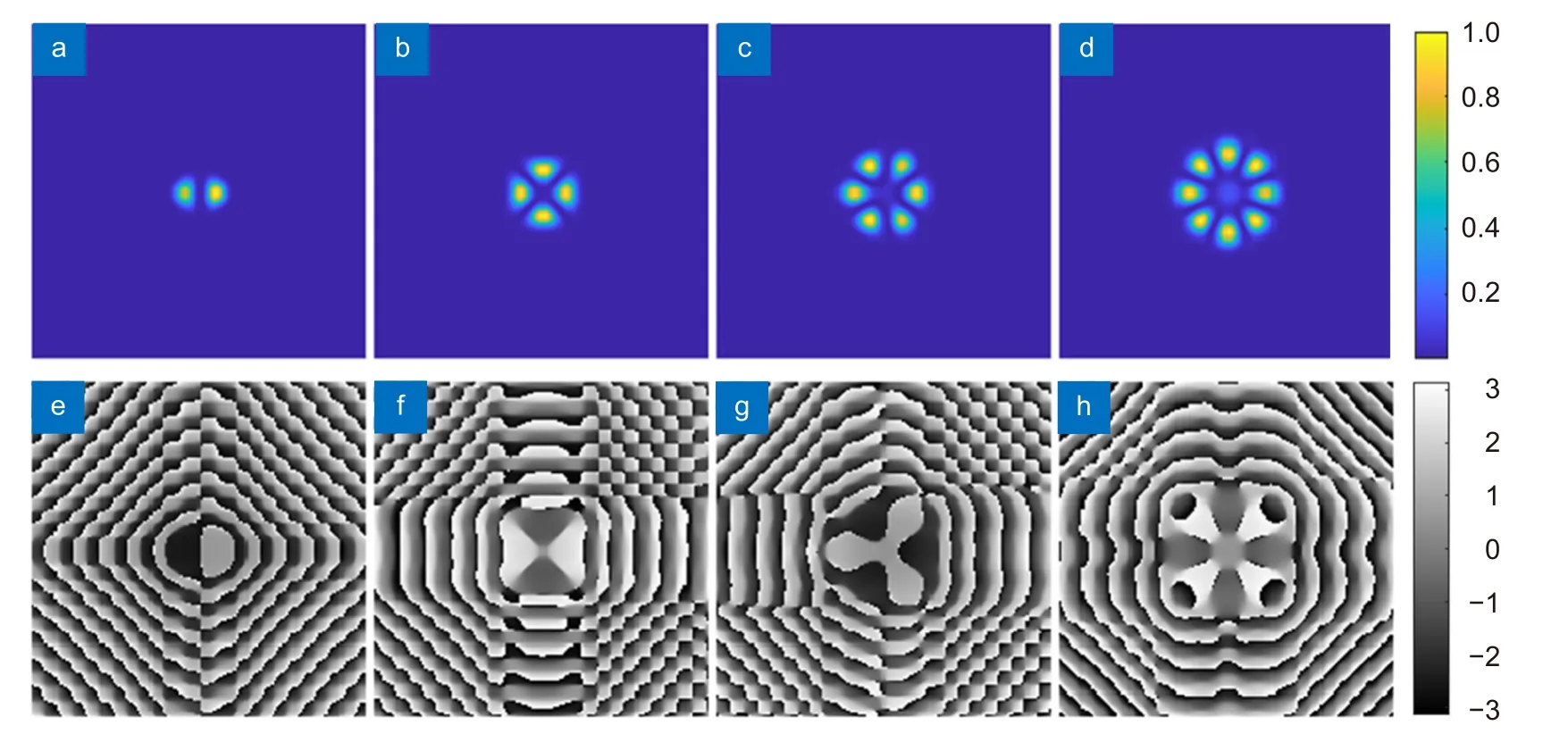
图12 叠加态拟合波前在滤波处理后的光场及相位。(a)～(d) 拓扑荷数分别为l=±1、±2、±3、±4 的拟合波前在u4 处的光强;(e)～(h) 拓扑荷数分别为l=±1、±2、±3、±4 的拟合波前在u4 处的相位Fig.12 The light field and phase of the superposition fitting wavefront after filtering.(a)～(d) Intensity of fitting wavefront at with topological chrages l=±1，±2，±3,and ±4 at u4;(e)～(h) Phase of fitting wavefront at with topological chrages l=±1，±2，±3,and ±4 at u4

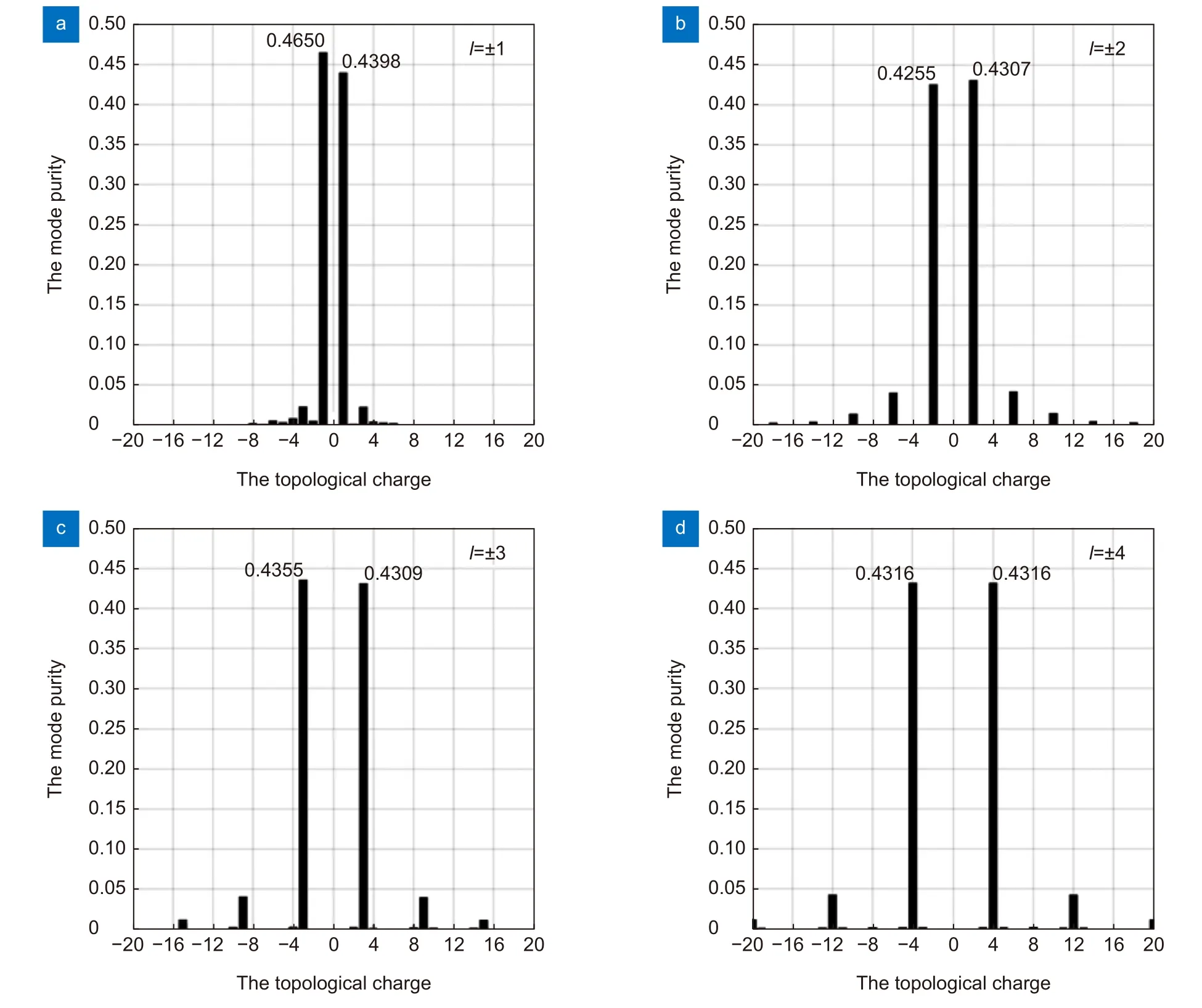
图13 叠加态拟合波前在滤波处理后的模式纯度。(a) l=±1；(b) l=±2；(c) l=±3；(d) l=±4Fig.13 The mode purity of the superposition fitting wavefront after filtering.(a) l=±1;(b) l=±2;(c) l=±3;(d) l=±4

3.5 动态调控

变形反射镜用本征模的方法对于目标波前的拟合所需时间很短，这使其具备动态调控涡旋光束的能力。当需要产生拓扑荷数为1～5 连续变化的光场时，只需将图3 (a)～3(e)中目标波前作为连续输入，即可得到图4、图5 中的连续输出。同样地，当需要产生连续旋转的涡旋光束时，也只需连续改变目标波前的初始角度即可。如图14 所示，分别是拓扑荷数为2 和3的拟合波前以单次60°旋转时得到的光场及相位。可以看出，本征模法可以很好地对任意旋转角度的涡旋光束进行拟合，角度的变换不会产生更多的误差，结合其拟合速度快的特点，可以很好地应用在涡旋光束的动态调控上。

图14 整数阶涡旋光束的动态调控。(a1)～(a6) 拓扑荷数为2 的光强；(b1)～(b6) 拓扑荷数为2 的螺旋相位；(c1)～(c6) 拓扑荷数为3 的光强；(d1)～(d6) 拓扑荷数为3 的螺旋相位Fig.14 Dynamic manipulation of integer order vortex beams.(a1)～(a6) Intensity with topological charge l=2;(b1)～(b6) Spiral phase with topological charge l= 2;(c1)～(c6) Intensity with topological charge l=3;(d1)～(d6) Spiral phase with topological charge l= 3

4 总 结

基于连续镜面变形反射镜，用本征模的方法，结合滤波处理，调控生成了拓扑荷数绝对值为5 以内的整数阶、分数阶、多分数阶和叠加态的螺旋波前，实现了对涡旋光束的动态调控。所得结果均较理想。对于整数阶涡旋光束，各个模式的模式纯度平均值为0.958，基本接近理想值。对于其他复杂涡旋光束，由本征模法得到的结果与目标波前得到的结果基本一致，可以认为基于连续变形反射镜的本征模法完全具备对这些涡旋光束的拟合能力。另外，本征模法计算速度很快，在涡旋光束的动态调控领域具有应用前景。

团队介绍

中国科学院光电技术研究所沈锋研究员团队主要从事激光光场调控及自适应光学技术的研究，涉及光场信息获取与处理、激光传输变换与控制等领域。参加并负责完成863 计划、国防预研等课题的研究。近年来开展涡旋光束的振幅特性、涡旋光束在大气湍流下的传输、涡旋光束及阵列的生成及检测、基于变形反射镜的复杂涡旋光束动态调控等领域的研究。获得国家科技进步一等奖、中科院科技进步一等奖、中科院杰出科技成就奖、中科院自然科学三等奖等多项奖项。发表学术论文40 余篇，申请及授权国防发明专利10 余项。