基于空间坐标与振动特征融合的机床切削状态分类方法
2022-12-15程晓斌
王 晶, 程晓斌, 高 艳, 王 勋, 杨 军
(1. 中国科学院噪声与振动重点实验室(声学研究所), 北京 100190; 2. 中国科学院大学, 北京 100049)
在机械加工中,使用独立的物理系统对机床切削参数进行监测可以直接感知物理信号的变化,反映机床实际的切削状态,判断其状态与生产计划是否一致,保证生产效率和生产质量[1]。在实际生产中,机床的硬件故障、数控系统故障和加工误差等因素会导致机床没有按照设定值正常运行[2]。具体表现为:(1) 硬件故障会导致机床切削参数未按指令值运行。例如主轴驱动故障会使主轴转速偏离设定值;弹性联轴器的开裂也会导致实际切深和切宽偏离设定值,使加工尺寸不稳定。(2) 数控系统故障会导致实际切削参数与指令值不一致。李梦群[3]指出数控系统故障会导致机床加工时执行数控代码语句错乱,未按生产计划运行,或机床坐标轴未按数控面板显示值移动,导致实际切深、切宽与设定不符。(3) 由零件装夹等人工操作带来的误差会使实际切削不符合设定的运动轨迹,且这些误差不能反馈至控制系统,导致实际切削量与计划值不一致[4]。因此有必要使用独立的物理系统监测实际切削参数,当计算出的切削参数受到物理信号异常影响与数控系统预定的参数值产生较大偏差时,可及时发现机床以非计划值运行现象。
监测机床的切削状态的常用手段是采集加工过程的振动信号[5],并从中提取特征来描述有关机床状态的信息。状态监测的研究主要包括三个模块,信号采集、特征提取和特征选择[6-7]和工作状态的分类[8]。为了全面描述复杂的切削过程和减小随机干扰对信号带来的影响,需要从振动信号中提取到丰富的特征构建高维特征池[9]。然而,高维特征池中存在非敏感特征,会干扰后续的分类准确率[10]。因此如选择有效特征,去除高维特征池中的不相关信息对切削状态分类尤为关键。
在工业中,流形学习被广泛地用于特征选择[11]。该算法通过非线性降维,能够消除或减少数据之间的多重耦合和非敏感特征的干扰,有助于更好地理解切削状态,建立更准确的分类模型。其中,t分布的随机邻域嵌入(t-distributed stochastic neighbor embedding, t-SNE)[12]是一种无监督算法,通过欧氏距离对数据点进行建模,捕捉局部结构的同时保持了全局结构,因此在工业状态监测领域被广泛地用作特征选择方法[13]。
然而,无监督的流形学习算法在实际工业环境中的灵活度有限。其应用于切削状态分类的局限性[14-16]主要体现在以下两个方面:(1) 在机床切削状态分类中,具有相同切削参数的振动信号通常被认为是同类数据。由于一些与切削参数无关的因素,如工件的切削位置、形状和刚度会在加工过程中不断变化,这会使系统的传递函数发生变化,最终导致同类数据的一致性差,样本发散度高。(2) 在精加工中,不同切削状态下的切削参数变化微小,从而使得t-SNE在特征空间中难以区分。在基于t-SNE的切削状态分类的应用中,应主要关注多种物理感知信息的融合与嵌入。
近年来,越来越多的研究关注将标签信息引入t-SNE以获得更好的性能。文献[17]引入了类标签信息,提出了有监督的随机邻接嵌入方法,以捕捉内在结构。基于数据标签的监督时间t-SNE[18]和深度监督t-SNE[19]被提出,来提取特征并学习数据的内在关系。在制造过程中,除了常用的振动信号,还有许多物理信息,如电流、力、坐标信息等都可以被测量,并作为信息嵌入。因此,本文旨在采用切削激励点的空间坐标嵌入t-SNE,以提取出更有区分度的特征,从而提高削状态分类的准确率。
本文提出了一种空间坐标嵌入的流形学习方法,基于振动信号构建高维特征空间,利用切削激励点的空间坐标修正样本分布,对机床的切削过程进行建模,命名为空间坐标嵌入的t-SNE(spatial coordinate embedded t-SNE, Ct-SNE)。Ct-SNE减小了振动特征空间中类内数据的差异,将相同切削参数的数据在高维空间中紧凑分布,以获得区分度更高的低维输出。在一台三轴立式铣床上进行了试验研究,收集了机床在多种切削状态下的振动信号和空间坐标作为数据集,对t-SNE和Ct-SNE的性能进行了比较和讨论。
1 t-SNE算法基本理论
由于高维特征池存在冗余信息,导致同类数据的一致性较弱,异类数据的相似成分过多,无法准确地反映机床的状态信息。因此需要对特征进行降维,选择出与切削状态密切相关的敏感特征,以提高状态分类的准确性。流形学习是一种基于拓扑流形概念的降维方法,可保留数据的本质结果,适合描述非线性过程,被用于特征选择。首先对流形学习中的t-SNE理论进行简单的回顾。
X={x1,x2,…,xn}⊆RD×n代表n个D维向量,作为t-SNE的输入,Y={y1,y2,…,yn}⊆Rd×n代表t-SNE处理后的低维输出。
对输入X,采用基于高斯分布定义的成对相似度pij表示样本间的相似关系,计算过程如下
(1)
式中:xi和xj是X中的样本;σi是xi的方差。
t分布用于描述低维数据的成对相似度,计算过程为
(2)
最终的输出Y由最小化概率分布P和Q之间的Kullback-Leibler散度获得,代价函数被定义为
(3)
2 空间坐标嵌入的t-SNE
对分类任务而言,有效的特征会将类内距离最小化,类间距离最大化。在本文的研究中,切削参数(包括主轴速度,进给速度,切削深度,刀具类型等)相同的状态被视为同一类别。振动信号虽包含丰富的信息,可以构建特征空间描述切削过程,但使用传统的无监督方法t-SNE难以捕获振动信号不同工况间的细微差异,使不同类别的特征在低维空间中产生交叠现象,最终使准确分类变得困难。且振动模式受到切削位置的影响较大,使样本发散程度高,不利于分类识别。为了获得更有效的特征,本文提出了一种空间坐标嵌入的t-SNE算法(spatial coordinate embedded t-SNE, Ct-SNE),将切削激励点的空间坐标作为监督信息引入到振动信号构建的特征空间中。
如公式(1)所示,t-SNE使用欧几里德距离表示样本之间的相似性。它遵循原始数据分布,没有任何监督信息。
数据xi和xj的欧几里德距离被定义为
(4)
为了提高t-SNE在特征选择时的有效性,Cheng提出了有监督的t-SNE的框架用于更精准的特征选择。其基本思想是使同类样本在特征空间中更接近,根据类别标签定义了样本间距离修正项
(5)
式中:τ∈(0,1)是一个常数参数是一个常数参数,表示缩小欧氏距离的尺度;c代表样本的类别。由公式(5)可知,同类点的距离按τ尺度被缩减,以强制增加样本间的相似度。异类样本间的距离没有变化,以保持原始分布。
在此方法基础上,本文结合切削过程,引入切削激励点的坐标至振动信号构成的特征空间,将修正项常数τ修改为与切削激励点的坐标相关的变量,以获取更高的灵活性,使类内样本的距离减小,而类间样本的距离增大。铣削过程为刀具作用在工件上的若干个连续冲击,是一个复杂的非线性过程[20]。其动态特性受多重因素影响,例如:工件的装夹位置、夹紧力度、激励点位置变化等。对铣削过程的振动分析通常是将工件划分为若干个微元体,并视同一个微元体的振动模态是相同的[21]。因此当刀具位置变化为小量时,振动信号声学特征的变化量可近似看成线性相关的,有较强的相似度。这里合理地假设来自相同切削参数的振动信号有着相似的基本分布,且切削激励点位的变化越小,振动信号的差异越小。为了使相同切削参数的样本具有更集中的分布,本文参考文献[22],定义了基于切削点空间坐标的距离修正项
(6)
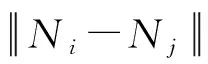
(7)
(8)
低维空间中的相似性和损失函数与t-SNE相同,如公式(2)和(3)中所示。
Ct-SNE算法的流程图如图1所示。首先使用振动信号构建高维特征集,并计算特征样本间的欧几里德距离;使用切削激励点的空间坐标计算距离修正项。结合欧氏距离和距离修正项计算高维样本间的相似度,并得到随机初始化的低维输出。之后使用Kullback-Leibler散度作为代价函数,迭代优化低维输出,最终得到最优的低维输出。
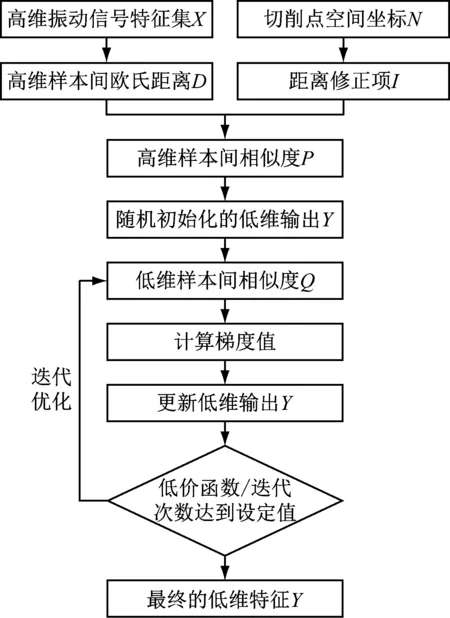
图1 空间坐标嵌入的t-SNE流程图
3 试验与分析
3.1 机床切削状态监测方法框架
机床切削状态分类系统可为加工过程提供有价值的信息,使用物理感知与数据驱动结合的方法,可以得到机床真实的切削参数,保证机床正常加工。其性能取决于它使用测量信号对不同切削状态分类识别的能力,状态监测的整体流程如图2所示。首先进行信号采集,采集的信号可以反映有关机械元件动态过程的信息,然后进行数据预处理,主要包括去除静默段信号、滤波、分帧和标注样本。再通过时域和频域中的分析方法对信号分析和特征提取,使用流形学习对高维特征进行特征选择。最终使用适当的分类器实现对当前状态的切削参数的识别。
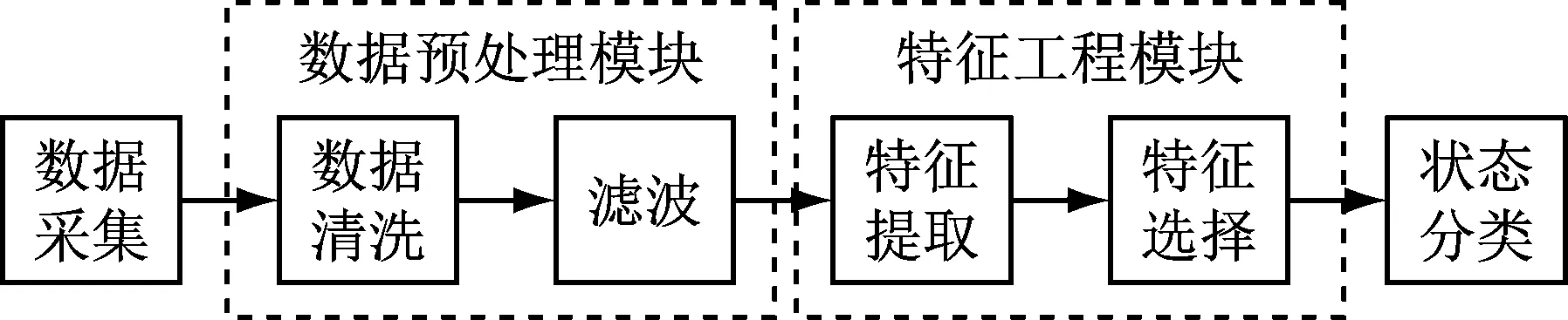
图2 切削状态分类流程图
3.2 数据采集
参照图3,数据采集试验是在VCM640三轴铣床上实施的,采集到了机床在不同的切削状态下的振动信号和空间坐标。机床上放置了一个加速度计来采集振动信号,三个光栅尺来采集X、Y和Z方向的位移变化。图3所示的光栅尺采集的是机床导轨X方向的位移,还有两个光栅尺分别平行安装于机床导轨Y方向和主轴Z方向。振动信号的采样频率为32 kHz,切削空间坐标的采样频率为1 kHz。关于采集到的振动信号和切削空间坐标的简要的介绍如下。

图3 数据采集示意图
(1) 振动信号。一个加速度计被放置在铣床的夹具上来收集振动信号。加速度计的频率响应在30Hz~10 kHz。加速度计被磁座固定在夹具上,该位置与切削点之间的传输路径短,且保证了刚性传输,使获取的信号的信噪比高。经过时域和频域分析,振动信号在本文中被提取为高维特征池。
(2) 切削点的空间坐标。切削空间坐标是由三个光栅尺测量得到的。两个光栅尺垂直安装在机床导轨下侧,用于收集X和Y方向的切削坐标;一个光栅尺与主轴平行放置,用于收集Z轴坐标。三维坐标表示真实空间中的切削位置,并被用作特征选择方法的嵌入信息。
3.3 数据描述
本文的试验的参数设置如表1所示,铣床以不同的切削状态加工铝制工件,刀具为硬质合金立铣刀。每次加工沿着X正方向进行。毛胚的每一层可以进行多次完整的加工。

表1 铣削试验设置
7类状态的切削参数如表2所列,其中变化了不同的切削深度、主轴转速、进给速率和刀具类型。相同的试验被重复五次,每次加工包括入刀、稳定切削和出刀。
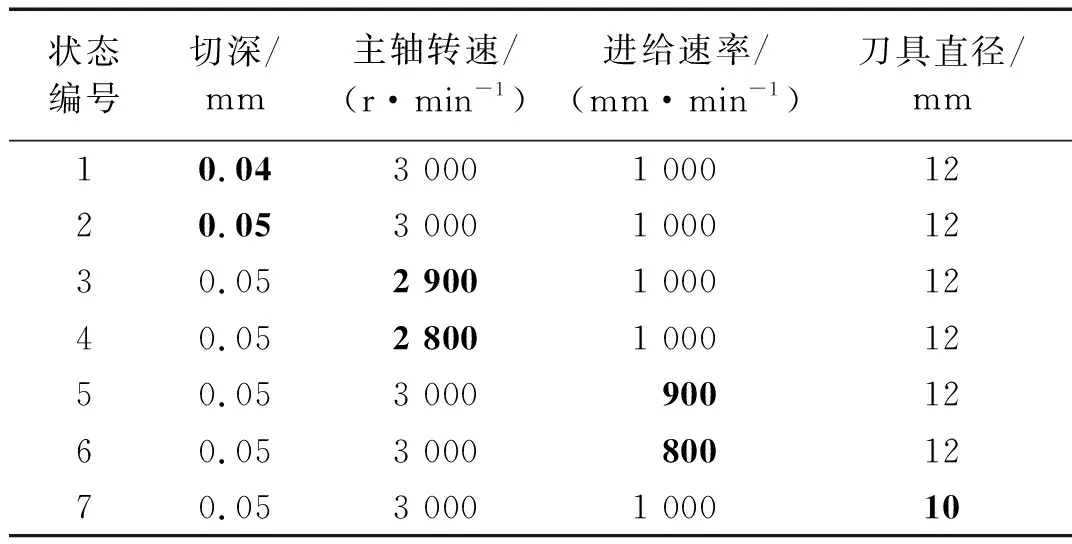
表2 不同切削参数下的切削状态
3.4 数据预处理
为保证信号的有效性,在信号采集后,使用巴特沃斯滤波器实现对振动信号进行30 Hz~5 kHz带通滤波。去除掉刀具与工件刚接触时产生的巨大冲击和未切削的静默段后,对有效切削信号进行分帧并标注。一个样本的时间长度为500 ms,步长为100 ms,每个切削状态包含3 000个样本。
图4绘制了每类状态一次完整的切削过程的振动时域图,包括入刀、稳定切削和出刀。入刀时,刀具与工件的接触由点逐渐变成半圆弧;当切削长度大于刀具的半径r时,刀具与工件的接触范围为半径r的半圆弧,之后的加工为稳定切削;出刀时,刀具与工件的接触逐渐从半圆弧变为一个点,直至刀具彻底离开工件。图5绘制了不同切削状态的功率谱密度。图4(a)绘制切削深度变化的振动信号时域图,不同切削深度的信号幅值差异很微弱。从频域图5(a)中,两种切削深度的功率谱密度曲线拟合程度很高,仅在3 500~4 500 Hz存在微弱差异。图4(b)、图5(b)绘制了不同主轴转速的信号图,可以看出在30~200 Hz内,低转速的功率谱密度值较大,在3 000~3 500 Hz内,高转速的功率谱密度值较大。图4(c)绘制了进给速率为800 mm/min和900 mm/min的振动信号时域图,该图显示了不同进给速率在固定长度的工件上进行完整切削一次的信号,由于状态6的进给速率小于状态5,因此使用切削状态6完成固定长度的切削需要花费更多的时间。在其频域图5(c)中,在3 000~5 000 Hz范围内,两状态有一定区分度。图4(d)、图5(d)绘制了不同直径的刀具对应的切削信号图,由于刀具直径差异较大,振动信号在时域、频域有着较高的区分度。从信号图可以看出,曲线的变化关系并不是线性的,这是由于机械加工是一个动态的非线性过程。机床由许多部件组成,如转子、轴承、齿轮等。每个部件都有几个独立的自由度,当改变某种切削状态时,一个部件的变化会影响到更多部件的状态,因此在测量信号中会出现非线性耦合,信号随某种参数的变化并不是单调的。

(a) 不同切削深度
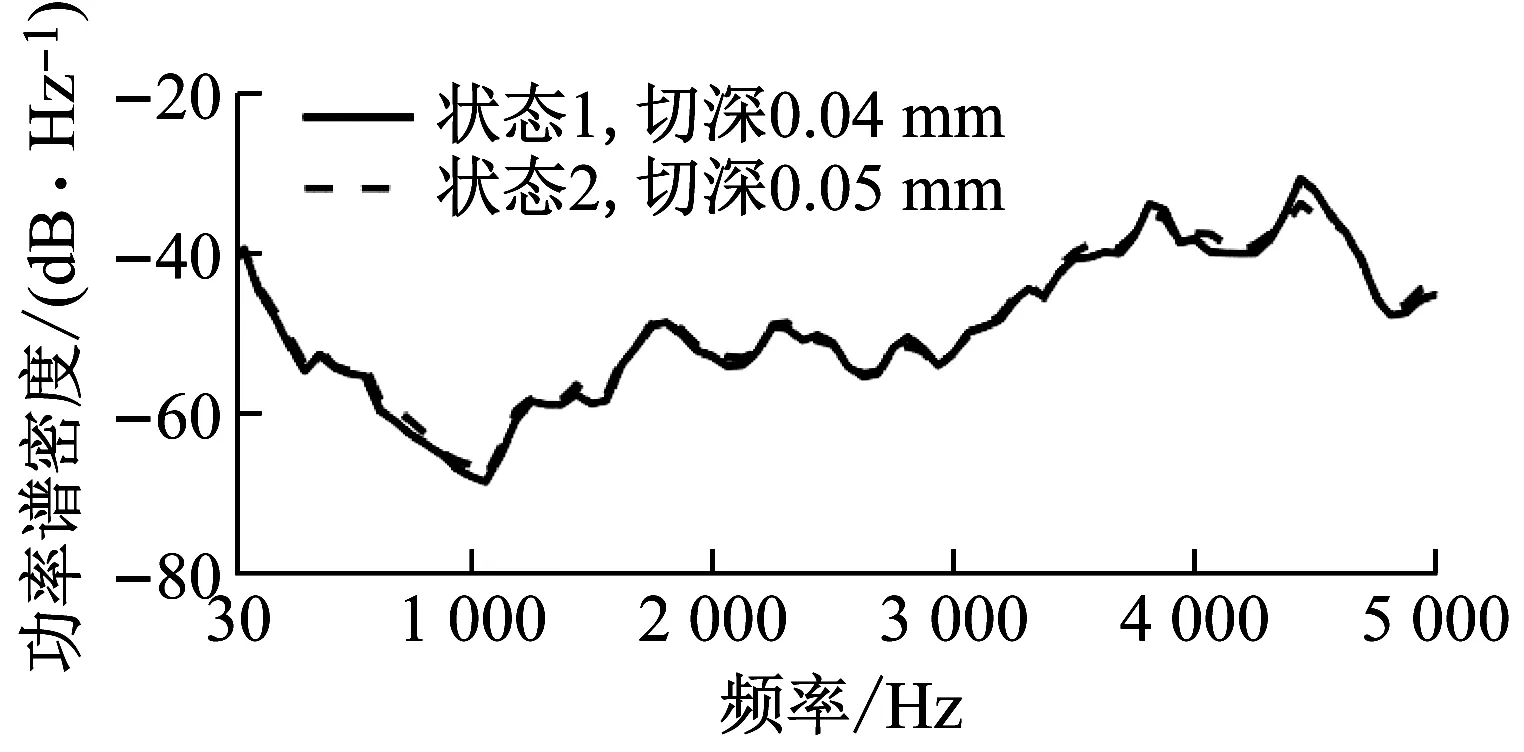
(a) 不同切削深度
另外,从时域图4中可以看出,每一次连续的切削过程都包括了入刀、稳定切削和出刀。入刀和出刀时的振幅大于稳定切削时的振幅。
图6绘制了由光栅尺采集到的状态2的六次切削过程的坐标变化情况。坐标变化与实际情况一致,沿着Y方向的反方向在X和Z方向上做六次往复运动。
3.5 特征提取
在制造过程中,加工状态种类的多样性和实测信号的随机性对机床状态分类是一项挑战。单一的特征可能不足以精准描述加工过程,确切的最佳特征是事先不知道的。因此,需要从振动信号中提取不同的时域和频域特征以生成高维的特征池,然后使用特征选择方法选择出有效的特征子集。对振动信号X={x1,x2,…,xn}⊆RD×n,本文选择了常用的十一种时域和频域特征来描述机械加工状态[23],构成了高维的特征池。
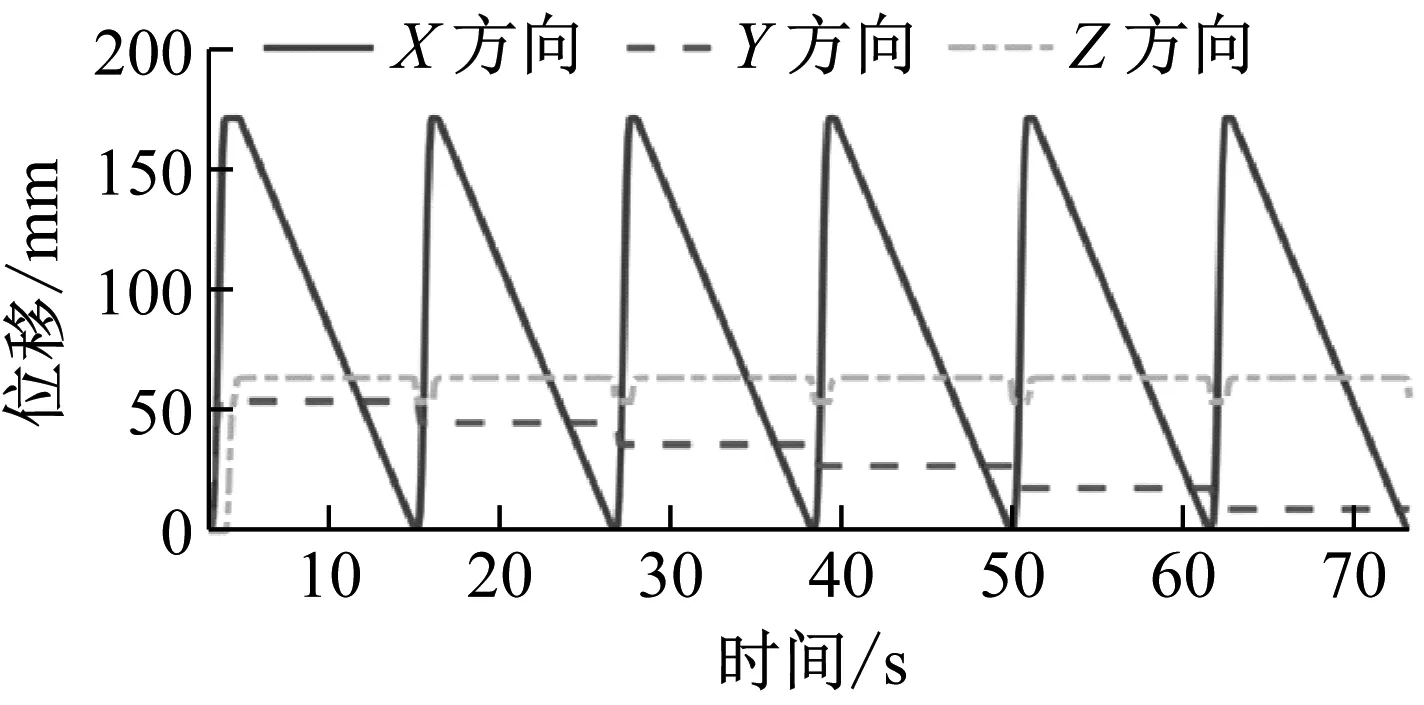
图6 连续六次切削X、Y、Z轴位移变化图

表3 由振动信号提取的特征
式中,p(f)为信号的功率谱。为了消除特征间单位和尺度差异的影响,本文对特征集进行了归一化处理,将特征值转化到值域空间[0,1]上。
4 结果与讨论
为了验证特征选择方法的有效性,本节进行特征可视化试验和分类试验来分析比较Ct-SNE与传统方法t-SNE的性能。
4.1 可视化试验
可视化试验比较了t-SNE和Ct-SNE在二维空间中的结果。这两种方法的参数按照文献[12]建议设置如下,困惑度设为经验值30,迭代次数t设置为1 000,动量项α(t)设置为0.8,学习率η初始设置为100,并在每次迭代后,它都会根据自适应学习率方案[24]进行更新。对振动信号提取的特征和光栅尺采集到的坐标信息做最大最小归一化。七类切削状态的二维嵌入结果如图7所示,其中每一个点代表一个样本,相同颜色相同标记的点来自一类切削状态。
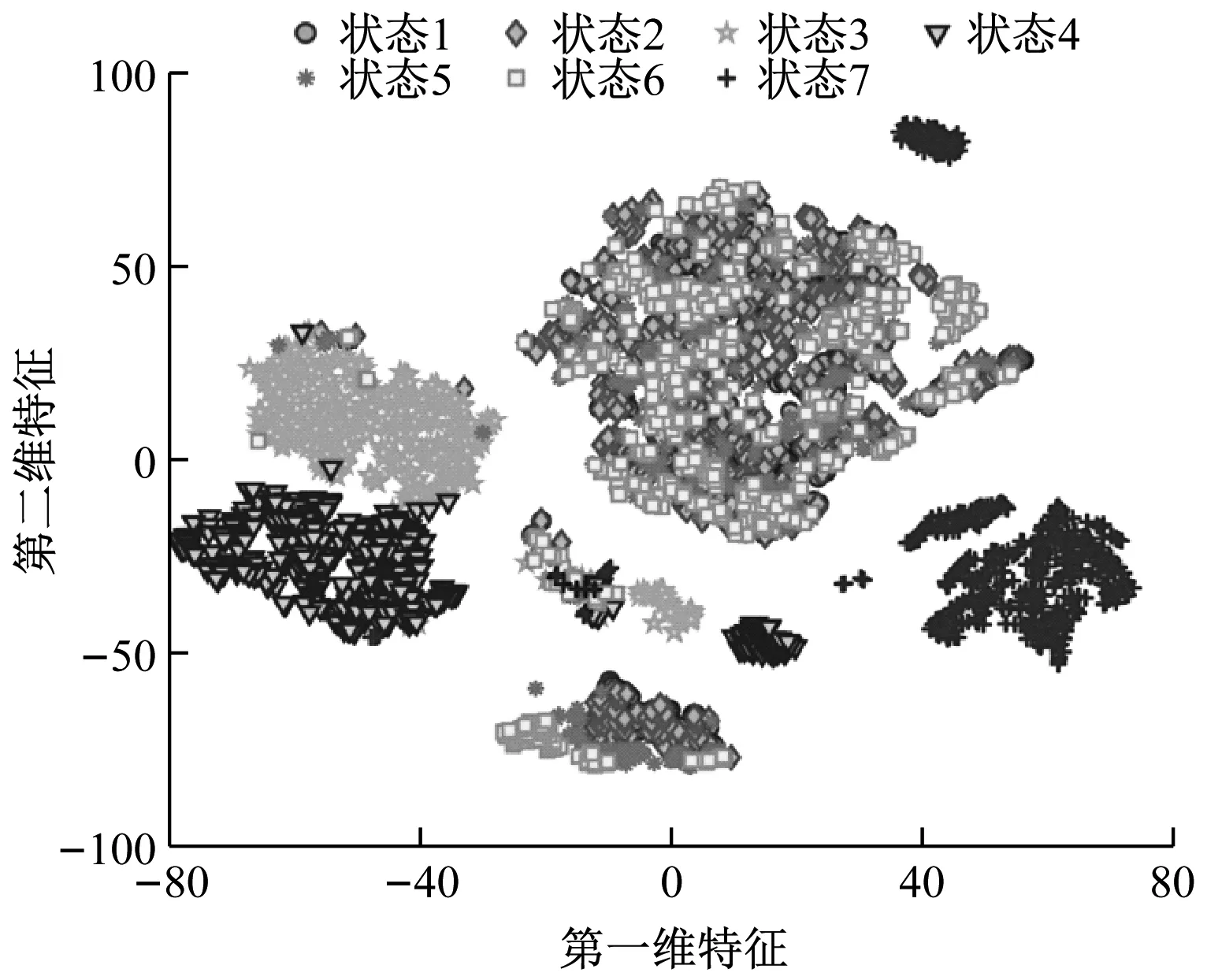
(a) t-SNE的二维嵌入结果
从图7(a)的结果可以看出:(1) t-SNE的二维结果混叠严重,变化切削深度和进给速率的状态(状态1、2、5、6)在二维空间区分度低。这是由于不同状态的参数差别很小,其振动特征相似性较高,大部分类别的样本在特征空间中区分度不大。状态3、4对应了不同的主轴转速,区分度高于不同切深的状态;因为状态7的刀具直径与其余状态相差较大,因此状态7也可以被有效区分。(2) 每个类别的样本发散程度高,形成多核聚类的现象。这是由于每一次完整的切削都包括入刀、稳定切削和出刀三个过程,参考图4可以得知,入刀和出刀的振幅明显大于稳定切削的振幅,因此入刀和出刀过程的数据与稳定切削的数据存在差异,在低维空间中被聚成了多簇。
图7(b)中Ct-SNE的结果显示,不同切削参数的特征区分度明显提高,类内特征的发散程度降低。这是因为切削激励点的空间坐标嵌入的的Ct-SNE方法在振动信号构成的特征空间中拉近了同类别特征的距离,使同类数据的相似度提高,从而使同一类别的数据分布更加紧凑。Ct-SNE算法可以使不同切削状态的区分度提高,因此可以考虑将Ct-SNE作为特征处理方用于机床切削状态分类。
4.2 最优维度选取
本文用到的特征选择方法t-SNE和Ct-SNE都涉及目标输出维度d。3.1节为了可视化结果更直观,将d的值设定为2。事实上,d对分类结果至关重要,因为如果d太小,会丢失太多的有效信息,而d太大,冗余或不敏感的特征会被保留。在分类试验中,K近邻算法被用于数据分类,按照经验将K近邻算法中的近邻数K设定为30,以获得不同d值的分类精度。使用10折交叉验证的方法。图8显示了t-SNE和Ct-SNE方法在不同维度上分类准确率。

图8 目标维度d对分类准确率的影响
在图8中,横轴代表不同维数的特征,纵轴代表分类准确率。t-SNE在四维特征上达到最佳分类准确率57.96%,Ct-SNE在五维特征上达到最佳准确率,准确率为96.78%。并且分类的结果与可视化结果一致,Ct-SNE在对特征进行非线性维数约减时有比t-SNE更好的表现。
4.3 特征选择算法用于切削状态分类
基于t-SNE和Ct-SNE的特征选择方法并不像线性降维方法那样提供从高维到低维空间的明确映射。然而,这一步对于机床状态分类是非常重要的,因为它必须处理训练样本集以外的新数据,这也被称为增量学习问题。迭代新增样本嵌入算法[25]被引入来解决增量学习问题。该方法先对新增样本进行局部线性重构,再通过迭代优化的方式优化低维输出特征。
为验证分类性能,引入了精度Precision(Pre)、召回率Recall (Rec)、F1-score(F1-Scr)和准确率Accuracy (Acc)四个指标[26]来评价这些特征选择方法的分类性能。分类设置与3.2节一致。在每种特征选择方法的最优维度上进行分类试验,这些性能指标在测试集中的结果如表4所示。
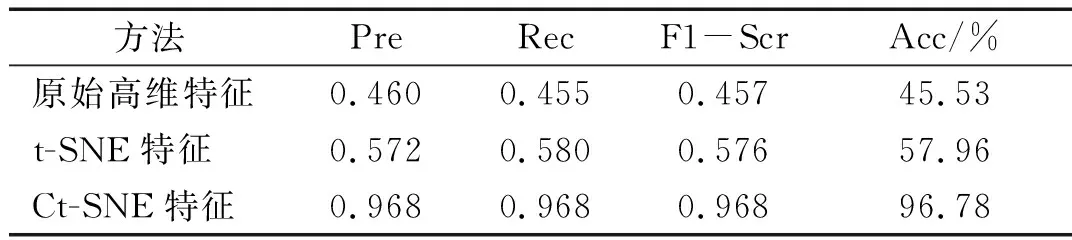
表4 不同方法分类评价指标
这四个评价指标的数值越大,意味切削状态分类的性能越好。从表4中可以看出,原始特征的分类性能较差,这是由于不同状态的差异较小,振动特征池中的冗余会干扰分类判决的准则。经过t-SNE选择后的特征的分类性能有了一定的提升,可以达到57.96%,说明t-SNE可以一定程度上去除特征池中的冗余和非敏感信息。通过引入切削激励点的的空间坐标,分类性能有了显著的提升,各项指标都在96%左右。这说明在空间坐标的约束下,同类数据特征的一致性变强,异类特征的区分度变高,从而提升分类性能。
为了获得更多分类结果的细节,图9和图10分别绘制了最优维度下的t-SNE特征和Ct-SNE特征的分类的混淆矩阵。
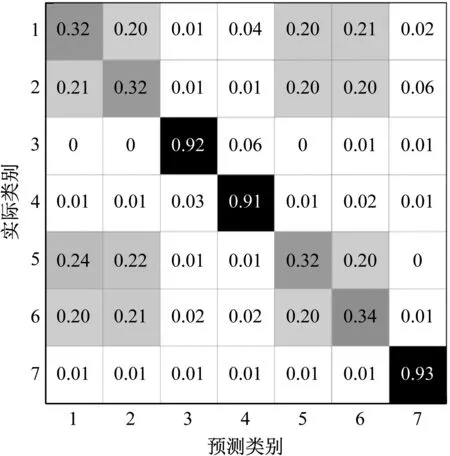
图9 t-SNE的四维特征分类混淆矩阵
由图9可见,状态1、2、5、6的分类准确度很低,大部分数据被错误地分到了不同切削深度或不同进给速率的状态中。这与可视化结果图7(a)一致,在仅使用振动信号时,不同切削深度和不同进给速率的数据在特征空间中难以区分,因此分类的错误率较高。而不同的主轴转速如状态3、4,与不同刀具直径如状态7,有较高的分类准确性。
图10显示了Ct-SNE的五维特征的分类的混淆矩阵。整体来看,分类准确性有了大幅度提升,各类别状态的分类准确率都达到94%以上。部分错误的分类是由特征解耦不彻底,数据存在少量混叠。例如状态1的部分数据被错分为状态2。状态5的少量样本落入了状态3的数据分布内。整体结果说明切削激励点的空间坐标的加入,对区分振动信号构成的特征起到了促进作用。
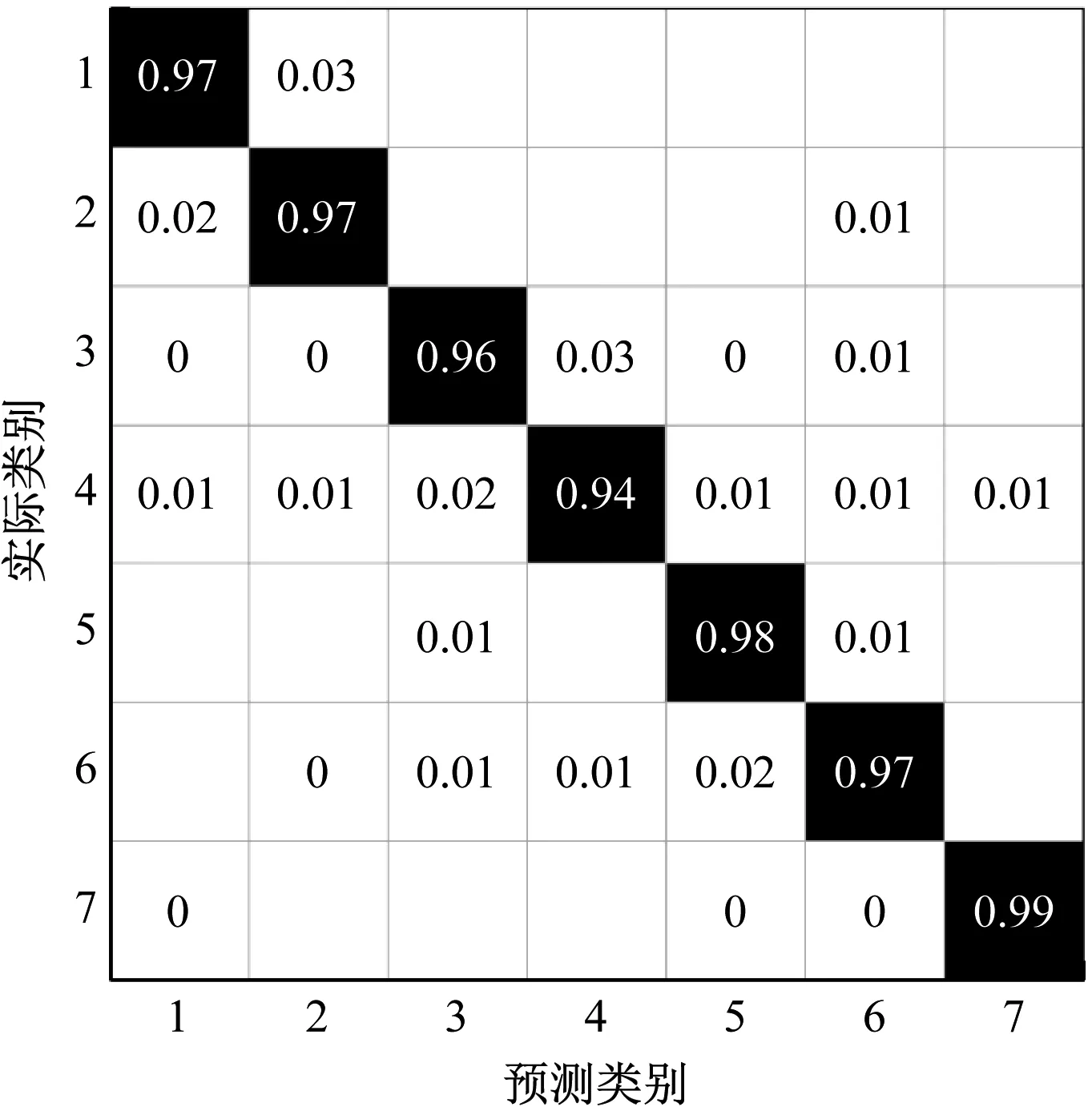
图10 Ct-SNE的五维特征分类混淆矩阵
5 结 论
为了提高切削状态分类的精度,本文融合振动信号特征与切削点的空间坐标,提出了空间坐标嵌入的t分布的随机邻域嵌入方法Ct-SNE,以选择有效特征用于机床切削状态分类。针对特征可视化结果和分类性能的评价标准展开分析,得到以下结论:
(1) Ct-SNE将切削空间坐标嵌入振动特征空间,构建了距离修正项,使类内数据分布更紧凑。从特征可视化的结果和分类性能的角度分析,该方法可提高不同切削参数振动特征的可区分度,进而状态分类的准确性,并优于无监督的流形学习方法t-SNE。
(2) 合适的目标特征维数可以获得更高的状态分类准确率。若维数过低,则损失过多有效信息,若维数过高,过多冗余会影响分类。
基于本研究所提出的空间坐标嵌入的t-SNE算法框架,将进一步开展多传感信号与加工状态的关联研究,获得更多维度的信息,以提升机床状态分类的准确率。
