基于泰森多边形的事故多发点识别方法*
2022-12-14刘戎阳郝妍熙刘志钢
刘戎阳,郝妍熙,胡 华,刘志钢,汪 涛
(1.上海工程技术大学 城市轨道交通学院,上海 201620;2.上海交通大学 船舶海洋与建筑工程学院,上海 200240)
0 引言
交通事故多发点的识别方法主要分为数理统计和空间统计2类[1],早期应用广泛的数理统计学方法有临界事故率法、质量控制法[2]、经验贝叶斯和全贝叶斯方法等[3],近些年空间统计方法如热点分析[4]、核密度分析[5]、基于路网单元分析[6]等方法逐步流行。空间统计分析方法可视化效果较数理统计更好,并能从多角度挖掘交通事故的空间分布特征[7]。
黄钢等[8]基于改进的密度聚类算法对无锡市交通事故多发点进行聚类,证明该算法的适用性;陆化普等[9]利用考虑路网的核密度分析方法和空间聚类分析方法,识别深圳市的事故多发点,并研究其分布特征;吴佩洁等[10]用时空立方体改进的热点分析方法研究小样本事故数据下中微观尺度的事故多发点;Colak等[11]基于网络空间权重的热点分析识别土耳其里泽的事故黑点;蒋宏等[12]用非参数核密度估计的方法构建路网单元,并对路网单元进行基于空间自相关性的聚类分析;姜燕等[13]以核密度估计和计数数据模型为基础,提出基于点模式和面模式的空间聚类分析模型。
然而,以上基于空间统计的事故多发点识别方法仍存在一些不足。其中,基于路网单元的事故多发点识别方法过于依赖城市路网数据,划分路网单元没有统一的合理标准[14],主观性过强,单元内部的情况也无法识别;核密度分析方法识别结果较粗糙,只能模糊确定大致的事故地点;热点分析、改进密度分析等空间聚类分析方法,受极值影响大,无法识别空间上相对独立的事故多发点。
鉴于以上空间统计方法的不足,本文提出基于泰森多边形的事故多发点识别方法,用泰森多边形划分空间统计单元,并补充相对独立的事故多发点,最后对识别出的多边形形状进行修正,使其能更好地表示事故的实际区域位置。研究结果可为道路交通管理提供参考和借鉴。
1 问题描述与建模
1.1 交通事故的可视化
本文数据来源于2018年江苏省盐城市122平台的报警数据,数据总量为63 483起,包含报警时间、报警地点、报警类型、报警内容等13个字段信息,本文经过筛选后选取39 884起交警记录为转交通事故的报警数据。
本文选取百度API进行地理编码,采用WGS84地理坐标系,经纬度保留小数点后6位,利用地理信息系统(GIS)进行二维可视化。由于部分事故点不在盐城市行政区范围内,因此用盐城市行政区矢量图对事故进行二次筛选,剔除非盐城市行政区内的交通事故,得到39 824起数据,事故点分布如图1(a)所示。统计各县域行政区事故数量,结果如图1(b)所示。从图1中可看出,亭湖区事故数量最多,盐都区其次,且事故主要集中在亭湖区和盐都区交界处。
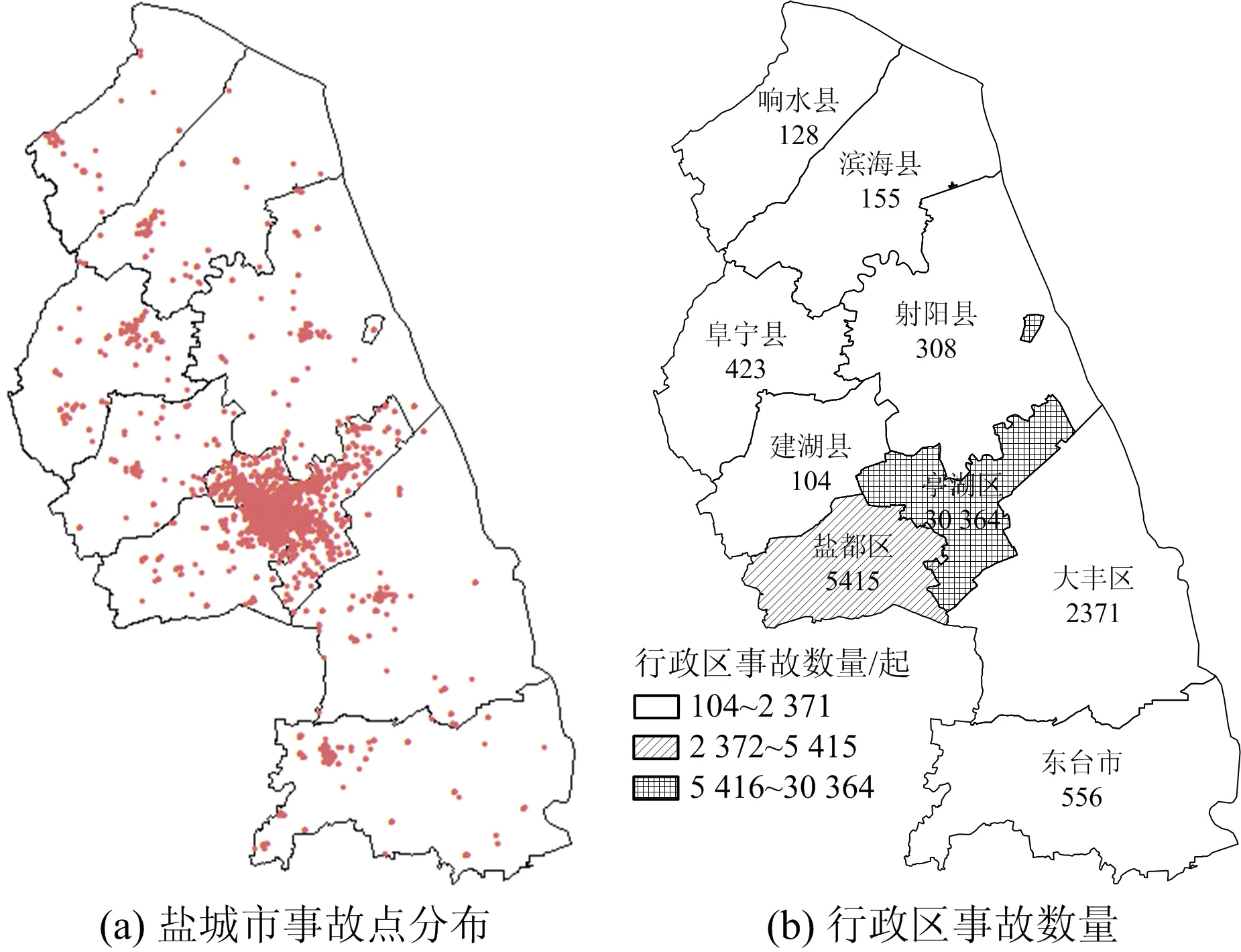
图1 盐城市事故分布情况Fig.1 Distribution of accidents in Yancheng
1.2 热点分析
基于路网单元、滑动窗体的事故多发点识别方法主观性强、适用性差,路网矢量数据较难获取且处理过程复杂,因此热点分析等空间聚类分析方法受更多学者的青睐。本文采用热点分析方法识别事故多发点,距离法采用欧氏距离,空间关系概念化方法选择反距离法,识别结果部分如图2所示。
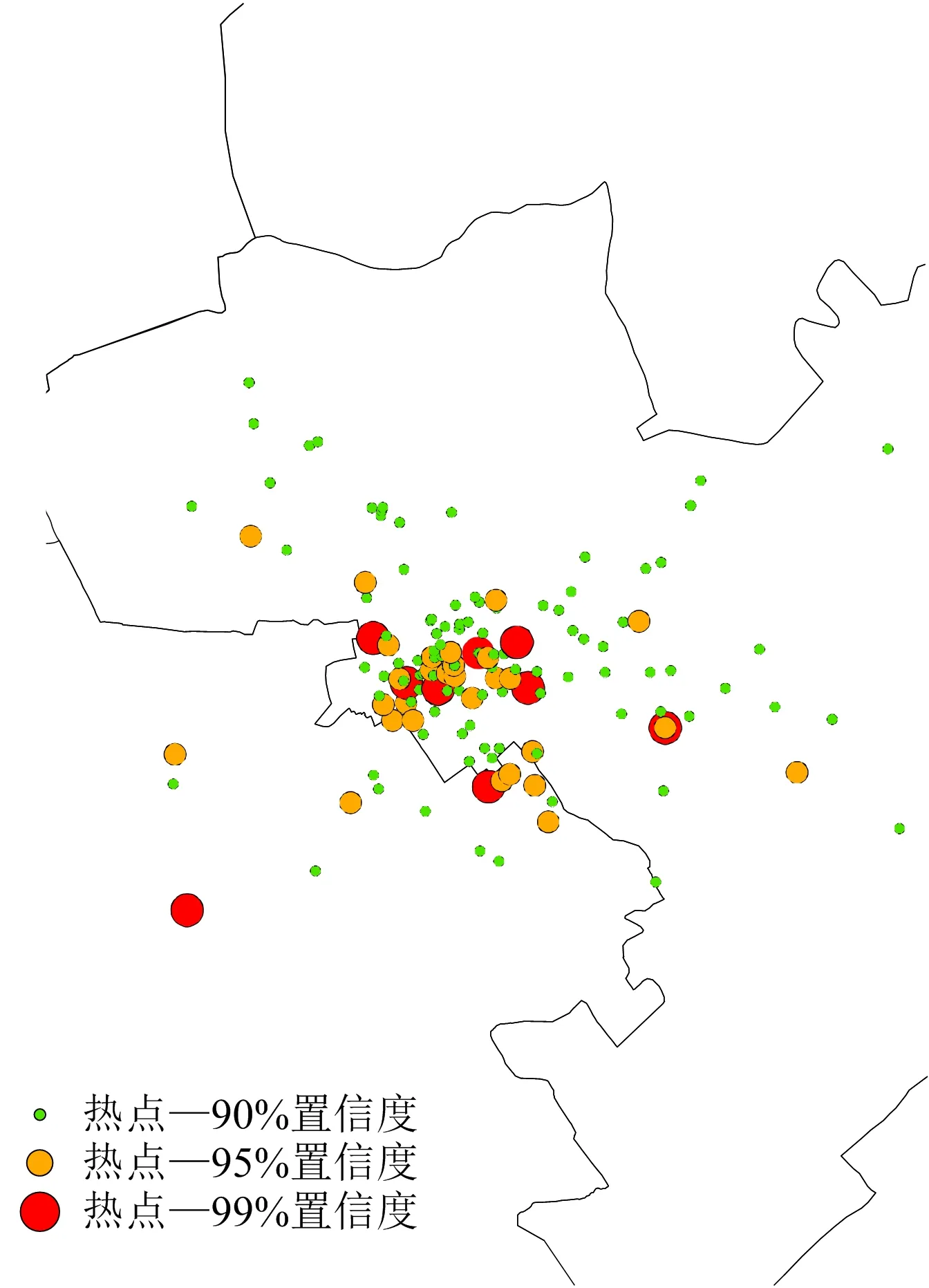
图2 热点分析结果Fig.2 Results of hot spot analysis
由于存在大量事故点重合,因此在进行热点分析前需将重合点合并,转换为加权点,权重为每个空间点的事故数量。加权后发现,存在极大值点,即部分点事故数量过大,相关参数如表1所示。由于部分极大值的存在,导致其它空间点的标准差偏小,最终致使热点分析结果中的热点数量偏少。同时,热点分析在原理上存在一定缺陷,无法识别出相对独立的高权重点,导致热点数量进一步减少。本文所用数据中,存在部分权重大于100的空间点,没有被识别为事故热点,而部分靠近极大值的权重60左右的点却被识别为事故热点,这符合热点分析原理,但显然是不符合现实的。
此外,由于热点分析识别出的结果为空间点,不是像基于路网单元、滑动窗体等方法结果为区域(面要素),而实际中的事故多发点应为热点及其周围的一小块区域,因此热点分析结果在实际中的应用效果不好,不能给出事故多发的区域。
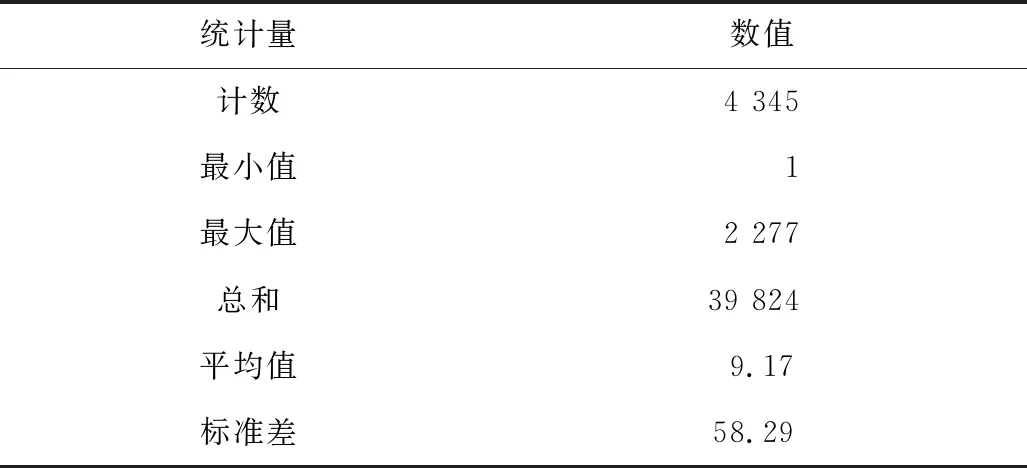
表1 加权点相关参数Table 1 Related parameters of weighted points
2 基于泰森多边形的事故多发点识别方法
由于上述热点分析存在的固有问题,本文提出1种基于泰森多边形的事故多发点识别方法。泰森多边形是将离散事故点构成三角网,作三角形各边的垂直平分线,将每个三角形的3条边的垂直平分线的交点连接起来得到的多边形。泰森多边形可以表征离散点的数据,同时具有以下3个特性:
1)每个泰森多边形内仅含有1个离散点数据。
2)泰森多边形内的点到相应离散点的距离最近。
3)位于泰森多边形边上的点到其两边的离散点的距离相等。
由于以上特性,泰森多边形可抽象理解为用离散点将空间平均划分,且离散点越密集区域的多边形面积越小,因此泰森多边形的面积可一定程度表征离散点的密度[15]。同时,泰森多边形能够充分反映其内部点的特性。
传统基于单元划分的事故多发点识别方法,是将整个平面或者路网缓冲区按固定大小的单元(多为矩形)进行划分,统计单元内的事故数量,以此来评价整个单元内部是否事故多发。泰森多边形不同于传统单元划分方法,其形状受离散点的分布而变化,每个多边形内部仅含有1个空间点,其多边形面积越小,则代表空间点分布越集中。交通事故往往在同一位置重复发生,同一空间点会存在多起事故,将同一空间点的事故数量转换为权重之后,可用来识别事故是否多发,权重越大,面积越小,则事故越多发。由于引入权重,会出现权重大,面积也大的情况,因此还需对泰森多边形进行形状修正。图3为本文所提出的基于泰森多边形的事故多发点识别方法流程。
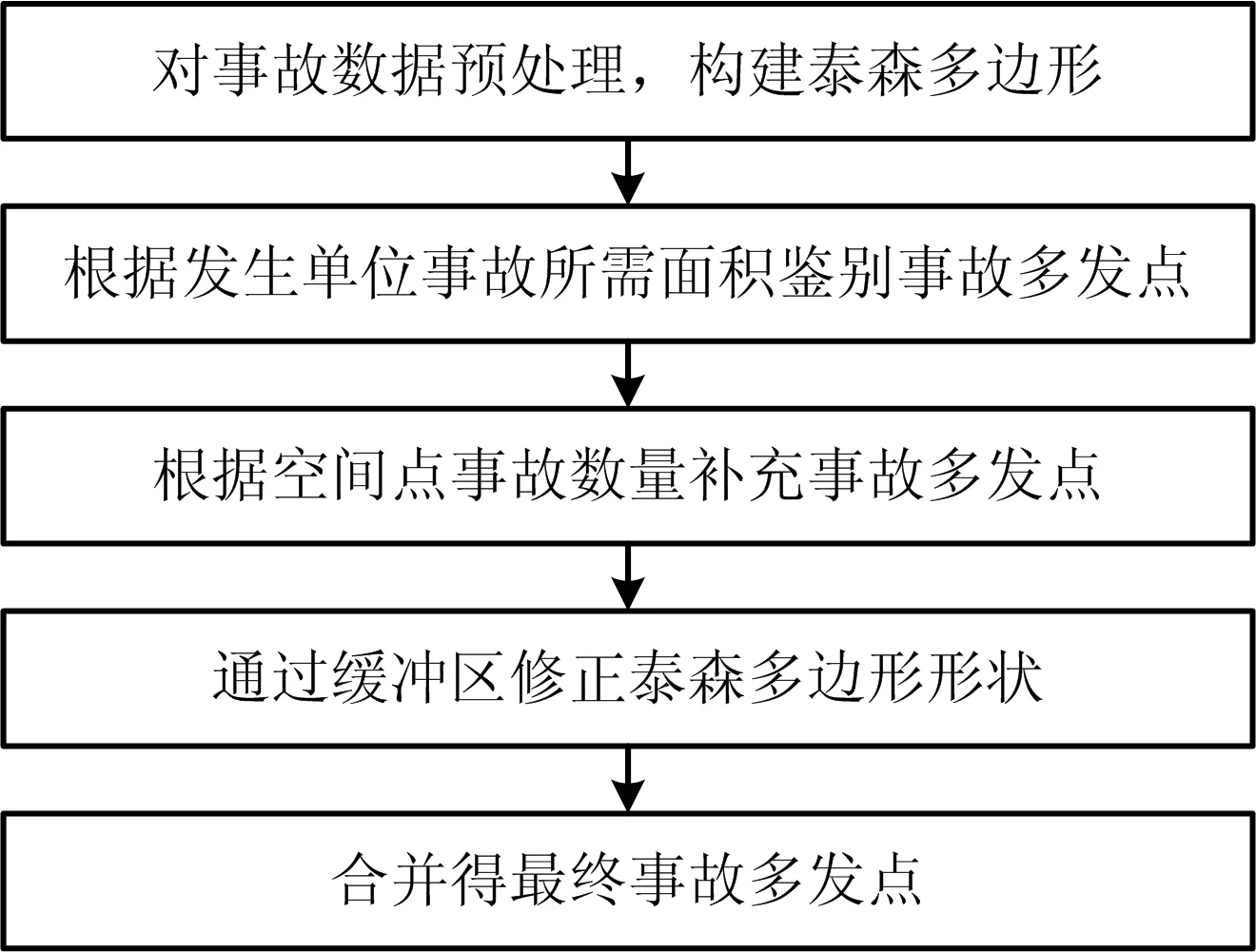
图3 方法流程Fig.3 Method flow chart
2.1 构建泰森多边形初步筛选事故多发点
将空间上重合点合并,并统计同一空间点上的事故数量,将其数量值赋值给空间点,由若干重合的事故事件点得到带权重的空间点,对这些空间点构建泰森多边形。计算构建的泰森多边形的面积,并将空间点的事故数量赋值给多边形。用多边形内(包含边界)的事故数量除以多边形面积,即可表征事故的密度,但由于事故数量除以面积时,若面积取km2或m2为单位,会导致密度数值上非常小,不利于识别事故多发点。因此用多边形面积除以事故数量来作为事故是否多发的评价指标,该值越大,即事故密度越低,事故发生越不频繁,评价指标记为W。
2.2 补充相对独立的事故多发点
存在部分空间点,此类点的权重值(事故数量)本身很大,即该地点发生大量交通事故,但是周围没有其他事故点,缺少约束从而导致构成的泰森多边形面积过大,进而使W值过大,因此需要对此类点建立缓冲区来补充事故多发点。

2.3 修正多边形形状
筛选后仍存在多边形面积过大的情况,为得到更精确的事故多发区域,需要对多边形形状进行修正。图4为3种修正形状的示意图,其中多边形为泰森多边形,圆形为缓冲区,点为事故点。
在H2中剔除S2,剩余缓冲区生成后与多边形集合相交,相交区域记为J,缓冲区面积为定值SH,多边形面积为S0,相交区域J的面积为SJ,并对以下3种情况进行修正:
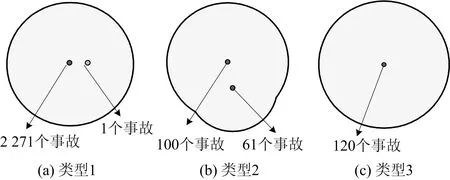
1)多边形为细长条状且不完全被缓冲区覆盖,事故点周围存在过近的相邻点,从而导致多边形面积过小的情况,可量化为SJ/S0 2)相交部分能覆盖大部分多边形,且缓冲区面积大于多边形面积,意味着缓冲区能覆盖大部分多边形,可量化为SJ/S0≥k3且SH/S0≥k4,保留泰森多边形作为事故多发点,如图4(c)所示。 3)若均不满足以上2种情况,则保留相交部分作为事故多发点。 以上3种修正后的图形集合记为S3。 将H1,S2,S3合并,将其重合部分融合,得到最终的事故多发点S。 为方便进行分析,本文自制事故多发区域的主要道路矢量图,最终得到的事故多发区域如图5(a)所示,与热点分析对比结果如图5(b)所示。本文所提方法最终得到的区域形状不一致且面积显著较小,其他单元划分方法结果的单元面积均较大,以路网单元划分方法为例,路网单元的宽度往往在10 m左右,而长度往往取500,1 000 m等,其得到的事故多发区域相对粗糙,缺乏对比意义。热点分析结果为点要素,能较好地体现事故点的空间分布规律,因此本文与热点分析作为参考,对比事故多发点(区域)的空间分布,以证明本文所提方法的合理性和优势。 根据图5可得,基于泰森多边形的事故多发点识别方法所识别出的事故多发点能较好地覆盖热点分析结果的热点,同时能够识别出热点分析无法识别的事故多发点。图6为热点分析中存在问题的3种类型,其中点为事故点,区域为本文所鉴别出的事故多发点。类型1如图6(a)所示,事故数量为1的点在热点分析中由于接近极大值点,因此被判别为90%置信度热点,显然是不合理的,本文提出的基于泰森多边形的事故多发点识别方法将2个点合并成1个区域,避免热点分析因靠近极大值而误判热点的情况。类型2如图6(b)所示,空间上相近的两点,其单独事故数量略少于其他热点,但其总和远大于部分热点,由于在热点分析原理上它们被单独计算标准差从而不够达到热点标准,但本文所提出方法将其所在区域合并为1个事故多发区域,更符合实际情况。类型3如图6(c)所示,该点事故数量大于部分热点,但因为其周围其他事故点较少,因此未被判为热点。 单从热点分析结果来看,由于北部存在较多高权重的事故点,中部点的权重值普遍没有北部大,南部也存在少量高权重的点,因此导致北部热点多,中部基本没有热点,南部少量热点的情况。而基于泰森多边形的识别方法补充中部地区相对独立的事故多发点,同时因为权重最大值2 277的存在,使得其他点的标准差较小,此方法也补充了受极值影响而减少的事故多发点。 1)本文所提出的基于泰森多边形的事故多发点识别方法能有效覆盖热点分析结果,能有效避免极值点的影响,充分体现事故多发点的空间分布特征。 图5 最终事故多发点对比Fig.5 Comparison of final accident-prone locations 图6 热点分析存在问题的事故点Fig.6 Accident locations with problems in hot spot analysis 2)经修正后的多边形面积较小,使事故多发范围更为精确,能更有效地为道路交通安全管理提供依据。2.4 最终的事故多发点
3 方法应用与结果分析

4 结论